【UnityShader入门精要学习笔记】(2)GPU流水线

本系列为作者学习UnityShader入门精要而作的笔记,内容将包括:
- 书本中句子照抄 + 个人批注
- 项目源码
- 一堆新手会犯的错误
- 潜在的太监断更,有始无终
总之适用于同样开始学习Shader的同学们进行有取舍的参考。
文章目录
- 上节复习
- GPU流水线
- 顶点着色器
- 裁剪
- 屏幕映射
- 三角形设置
- 三角形遍历
- 简单拓展:重心坐标系
- 片元着色器
- 逐片元操作
- 总结
上节复习
在上节笔记中,我们学习了图像渲染流水线的基本过程,从应用阶段的CPU处理,输出渲染图元到几何阶段,再输出屏幕空间的顶点信息到光栅化阶段。
上节详细介绍了应用阶段,在这一阶段主要由我们人为控制,在程序中设定材质,网格,纹理,着色器等数据的渲染,并对不必要的渲染进行剔除。整个渲染流程是从硬盘加载数据到RAM再到VRAM由显卡进行调用,RAM中的数据在被调用到VRAM后就会被丢弃(除了部分用于进行物理计算的网格信息),所有工作在渲染状态中打包成数据准备好后,将由CPU进行DrawCall来通知GPU对相应的图元(primitives)进行处理。那么接下来就是GPU流水线阶段,也对应了我们后面的几何阶段和光栅化阶段。
GPU流水线
在GPU流水线阶段,开发者无法完全操控整个GPU流水线,不过GPU还是为我们提供了一些阶段的控制权,如下图所示:
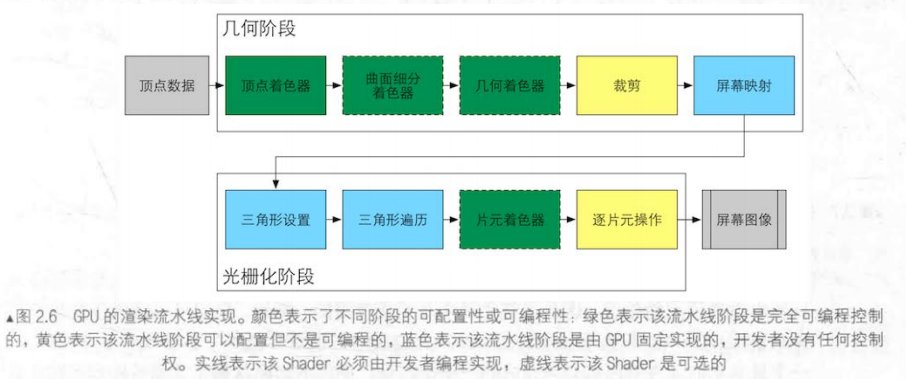
上图可以抽象成2个大阶段,其中起点是接收应用阶段加载到显存的顶点数据,准备好了由CPU通过DrawCall调用GPU。接下来就是GPU的处理流程,几何阶段和光栅化阶段。最后处理完成输出为屏幕图像。
接下来是书中的介绍,请对照上图查看,可能初学会难懂拗口,不过没关系,先记个名字,后续会逐一介绍。
在几何阶段,顶点着色器(Vertex Shader) 是完全可编程的,它通常用于实现顶点的空间变换,顶点着色等功能。曲面细分着色器(Tessellation Shader) 是一个可选的着色器,用于细分图元。几何着色器(Geometry Shader) 也是可选的着色器, 可以被用于执行逐图元(Pre-Primitive) 的着色操作,或者被用于产生更多图元。(其实这三个阶段可以简单理解为点到线到面的处理,在我理解里几何阶段就是一种对图元在几何性质的点线面上的规划和渲染)
经历了着色器渲染后,接着进行裁剪(Clipping) ,这一阶段的目的是将那些不被渲染的顶点裁剪掉,并剔除某些三角面元的面片。这一阶段我们可配置但不可编程(也就是说我们只决定裁剪哪些,而裁剪的算法是固定的)。我们可以使用自定义的裁剪平面来配置裁剪区域,也可以通过指令控制裁剪三角图元的正面还是侧面。(接触过Shader中的Clip的同学们应该更有体会)
几何阶段的最后一个流水线是屏幕映射(Screen Mapping) ,这一阶段是不可配置和编程的,它负责把每个图元的坐标转换到屏幕坐标中,毕竟在从CPU到GPU处理这些数据的时候,它们常常不是在同一个坐标空间下的。
接着是光栅化阶段,其中的三角形设置(Triangle Setup) 和三角形遍历(Triangle Traversal) 阶段都是固定函数(Fixed-Function)的阶段。接下来的片元着色器(Fragment Shader) 则是完全可编程的,用于实现逐片元(Pre-Fragment) 的着色操作,在逐片元操作(Pre-Fragment Operations) 阶段负责执行很多重要的操作,例如修改颜色、深度缓冲、进行混合等,它不是可编程的,但具有很高的可配置性。
上述内容看着复杂,但是学习shader必须掌握的,接着我们要一一描述这些概念
顶点着色器
顶点着色器(Vertex Shader) 是流水线的第一个阶段,学习几何的时候总是由点到线到面嘛。它的输入来自于CPU,对每个输入的顶点都会调用一次顶点着色器。它本身不创建或销毁顶点,无法得到顶点与顶点的关系,因此它无法判断某几个点是不是同属于一个三角网格。由于其独立性,只要计算就好了,因此顶点着色器处理速度也很快。
顶点着色器主要完成的工作是:坐标变换和逐顶点光照。除此之外还可以输出后续所需的数据。下图展示了顶点着色器对顶点进行坐标变换并计算顶点颜色的过程:
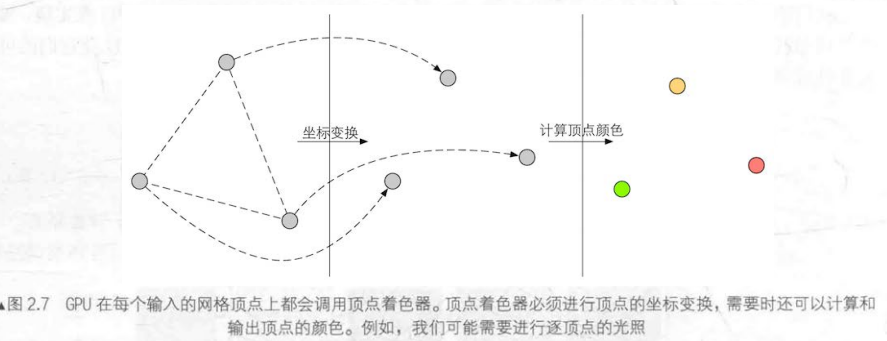
我们可以通过坐标变换改变顶点位置,从而实现顶点动画,例如模拟水面,布料等等。但无论我们在顶点着色器中如何改变顶点的位置,一个最基本的顶点着色器必须完成的一个工作是:把顶点坐标从模型空间转换到齐次裁剪空间 。
在顶点着色器中可能会经常看到如下代码:
o.pos = mul(UNITY_MVP, v.position);
上述代码的功能就是将顶点坐标转化为齐次坐标,通常再由硬件做透视算法后,最终得到归一化的设备坐标(Normalized Device Coordinates,NDC)。(其实看到归一化不少同学可能就理解了,就是为了将不同坐标转化到同一个齐次坐标再进行处理嘛)
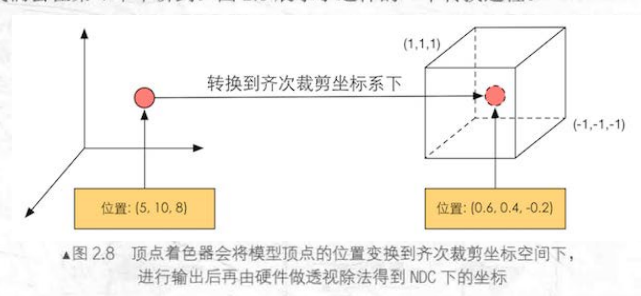
(上图给出的分量范围是OpenGL同时也是Unity使用的NDC,z分量范围为[-1,1]。在DirectX中z分量范围为[0,1])
(左图是模型空间,右图是NDC,齐次裁剪坐标空间是四维的)
顶点着色器可以有不同的输出方式,最常见的输出路径是经光栅化后交给片元着色器进行处理,而在现代的Shader Model中还可以将数据发送给曲面细分着色器或几何着色器。
裁剪
为什么裁剪。简单来说我们不需要渲染不在摄像机视野内的物体,因此这些部分需要被裁剪掉。
一个图元和摄像机的视野有三种位置关系:完全在视野内,部分在视野内,不在视野内。完全在视野内的处理完就传递给下一个流水线阶段,不在视野内的就不传递,因为它不显示也就不参与渲染,而部分在视野内的则需要进行裁剪处理:例如,一条线段的一个顶点在视野内,而另一个顶点不在视野内,那么在视野外部的顶点应该使用一个新的顶点来替代,这个新顶点位于线段和视野边界的交点处。
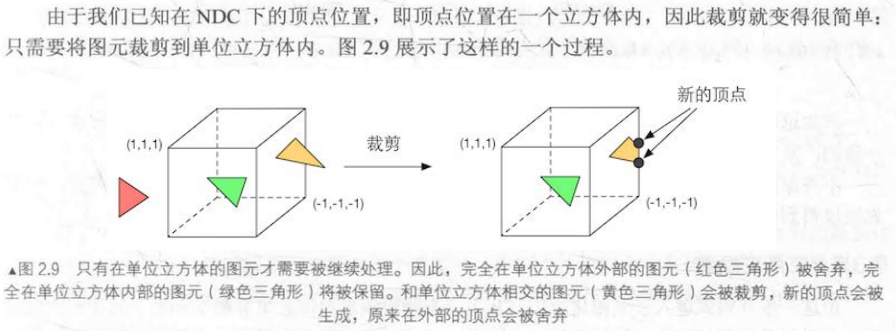
(上图的单位立方体代表的是NDC,而实际裁剪工作是在裁剪空间内完成的)
如上图所示,视野边界就是NDC的坐标分量的上界和下界,我们绘制NDC的单位立方体,则保留在立方体内的部分进行渲染,被立方体边缘裁剪的部分产生新顶点。
虽然我们无法通过编程来控制裁剪的过程,不过是可以自定义裁剪操作的。
屏幕映射
屏幕映射是几何阶段的最后一步,其输出将作为光栅化阶段的输入。这一步接收的输入坐标是归一化的齐次坐标。屏幕映射(Screen Mapping) 的任务是将每个图元的x和y坐标转换到屏幕坐标系(Screen Coordinates) 下。屏幕坐标系是一个二维坐标系,它和我们显示画面的分辨率相关。
实际上屏幕映射就是二维上对齐次坐标的缩放变换。屏幕坐标系的最小坐标是左下角(x1,y1),而最大坐标是右上角(x2,y2),与图元的齐次坐标系是不一样的。
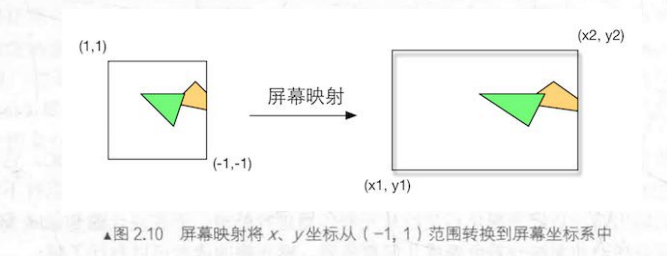
(屏幕映射对齐次坐标进行了x和y分量上的缩放变换,并且对应的坐标也改变了,其中x1<x2且y1<y2)
那么z轴呢?z跑哪里去了?屏幕映射不会对z轴进行任何处理,屏幕坐标会和z轴一起构成一个新坐标系,称为窗口坐标系(Window Coordinates) ,这些值会被一起传递到光栅化阶段。
屏幕映射得到的屏幕坐标决定了这个顶点对应屏幕上哪个像素以及离这个像素有多远。
此外,OpenGL和DirectX的屏幕坐标也存在差异,OpenGL将屏幕左下角作为最小窗口值,而DirectX将屏幕右下角作为最小窗口值。
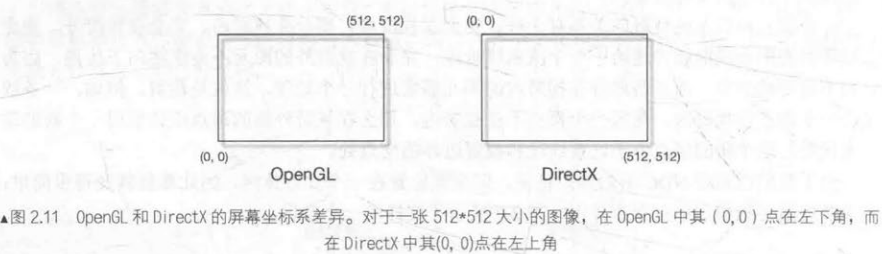
如果你发现得到的图像是倒转的,那么很有可能就是这个原因造成的。
三角形设置
三角形设置是光栅化的第一个阶段,上一个阶段屏幕映射给出了屏幕坐标系下的顶点信息和其他额外信息,例如深度值(z坐标),法线方向,视角方向等。光栅化阶段有两个重要的目标:计算每个图元覆盖了哪些像素,以及为这些像素计算它们的颜色。
三角形设置会计算光栅化一个三角网格所需的信息。具体来说,在几何阶段输出的都是三角网格的顶点,即我们所得到的是三角形网格每条边的两个端点。但如果需要得到整个三角网格对像素的覆盖情况,我们就必须计算每条边上的像素坐标。为了能够计算边界像素的坐标信息,我们就需要得到三角形边界的表示方式。这样一个计算三角网格表示数据的过程叫做三角形设置。
说白了,说人话就是连线,把点连成三角形或者边。
三角形遍历
三角形遍历阶段会检查每个像素是否被一个三角网格所覆盖。如果被覆盖的话,就会生成一个片元(fragment) 。而找到哪些像素被三角网格覆盖的过程就是三角形遍历,这个阶段也被称为扫描变换(Scan Conversion) (我想是因为扫描线算法?)。
根据三角形设置的计算结果来判断每个像素是否被一个三角网格覆盖,并使用三角网格3个顶点的顶点信息对整个覆盖区域的像素进行插值。下图展示了三角形遍历阶段简化的计算过程:
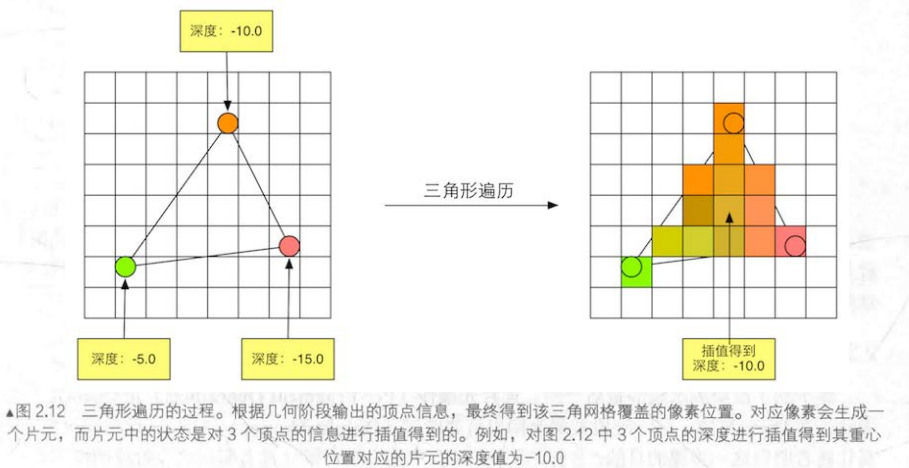
这一步的输出结果得到一个片元序列。一个片元并不是真正意义上的像素,而是包含了很多种状态的集合,这些状态用于计算每个像素的最终颜色(最终结果)。状态包括且不限于:屏幕坐标,深度信息,以及其他从几何阶段输出的顶点信息,例如法线、纹理坐标等。
(图元和片元虽然在英文上是fragment,如果翻译成碎片很容易被误解为个体,实际上它们应当被视为多种状态的集合,一个元包括了很多的信息,而不仅仅是某个图形或者某个像素)
简单拓展:重心坐标系
推荐阅读计算机图形学 1:重心坐标系(Barycentric coordinate system)详解
上图展示的片元颜色渲染,我们看到重心插值的深度为-10。既然要计算插值,如果我们以三角形某一个顶点为原点,去构建一个直角坐标系再计算,显然并不是那么好,最简单的方案构建一个非正交的坐标系,这个坐标系就是重心坐标系,请看下图:
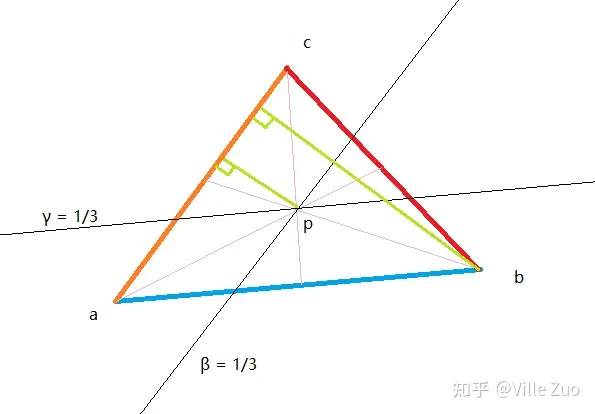
上图三角形,以abc代表顶点。假设我们以点 a a a为原点,那么 a b → = b − a \overrightarrow {ab} = b-a ab=b−a, a c → = c − a \overrightarrow {ac} = c-a ac=c−a。如果以 a b → , a c → \overrightarrow {ab} ,\overrightarrow {ac} ab,ac作为基向量建立坐标系。 p p p点为三角形的重心,设 p p p点的坐标为 ( β , γ ) (\beta,\gamma) (β,γ),那么点 p p p的坐标表示即为:
p = a + β a b → + γ a c → p= a + \beta \overrightarrow {ab} + \gamma \overrightarrow {ac} p=a+βab+γac
p = a + β ( b − a ) + γ ( c − a ) p= a + \beta (b-a) + \gamma(c-a) p=a+β(b−a)+γ(c−a)
p = ( 1 − β − γ ) a + β b + γ c p= (1-\beta - \gamma)a + \beta b+ \gamma c p=(1−β−γ)a+βb+γc
因此令 ( 1 − β − γ ) = α (1-\beta - \gamma) = \alpha (1−β−γ)=α 即为:
p ( α , β , γ ) = α a + β b + γ c p(\alpha,\beta,\gamma)= \alpha a + \beta b+ \gamma c p(α,β,γ)=αa+βb+γc
其中 α + β + γ = 1 \alpha+\beta +\gamma = 1 α+β+γ=1
好了,这样重心坐标系就建立好了。在这个坐标系下,三角形内任意一点的位置可视为三个顶点的线性组合,通过重心坐标系我们可以很简单判断某个点是否在三角形内部,只需
0 < α < 1 , 0 < β < 1 , 0 < γ < 1 0<\alpha<1,\newline 0<\beta<1,\newline 0<\gamma<1\newline 0<α<1,0<β<1,0<γ<1即可
当 α = β = γ = 1 3 \alpha = \beta = \gamma = \frac{1}{3} α=β=γ=31时则为重心位置。
片元着色器
片元着色器(Fragment Shader) 是另一个非常重要的可编程着色器阶段,在DirectX中,片元着色器也被称为像素着色器(Pixel Shader) ,但是我们说过片元包含像素,但不等同于像素,所以片元着色器是更适合的名字。
前面的光栅化阶段实际并不影响屏幕上每个像素颜色,而是产生一系列数据信息,用于描述一个三角形网格是怎样覆盖每个像素的,而每个片元负责存储这一系列信息。真正会对像素产生影响的是逐片元操作(Pre-Fragment Operation)阶段 。
片元着色器的输入是三角形遍历阶段对顶点信息进行插值后得到的结果,更具体的说是对顶点着色器的输出数据进行插值后得到的。而片元着色器的输出是一个或多个的颜色值,如下图所示。
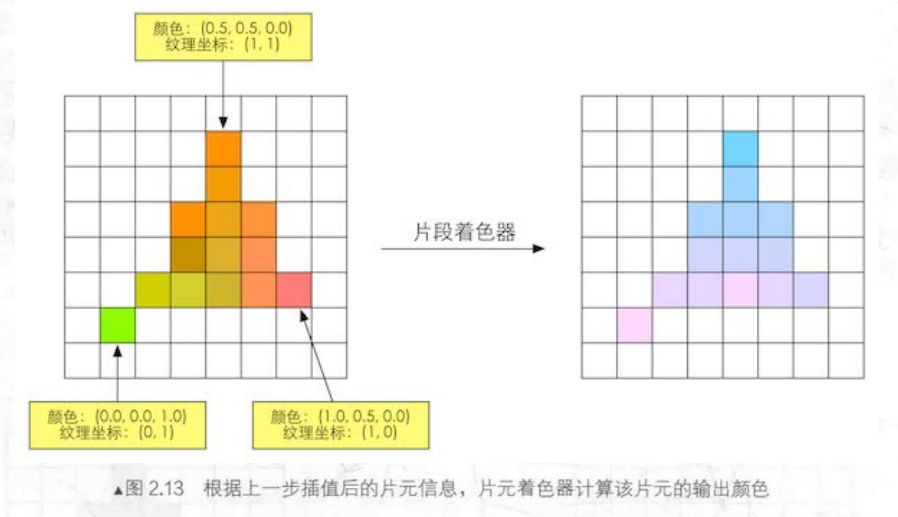
在这一阶段会完成许多重要的渲染技术,其中最重要的技术之一就是纹理采样,为了在片元着色器进行纹理采样,我们会在顶点着色器阶段输出每个顶点对应的纹理坐标,经过插值之后就能得到其覆盖的每个片元的纹理坐标了。
虽然片元着色器很重要,但其局限性在于仅能影响单个片元。也就是说当执行片元着色器时,它不可以将自己的任何结果直接发送给它的邻居(相邻的其他片元)。除了当片元着色器可以访问到导数信息(gradient或者说derivative)时例外(本章拓展阅读部分补充)。
逐片元操作
最后一步是逐片元操作,在DirectX中称为输出合并阶段(Output-Merger)。最主要的目的还是Merge合并,合并的目标就是每一个片元。
这一阶段有几个主要任务:
- 决定每个片元的可见性。这涉及很多测试工作,例如深度测试、模板测试等。
- 如果一个片元通过了所有的测试,就需要把这个片元的颜色值和已经存储在颜色缓冲区中的颜色进行合并,或者说是混合。
首先要进行的就是片元测试,这些测试决定了哪些片元可以被渲染,哪些片元会被舍弃。简单来说就是一个资格考试,淘汰不合格的片元。只要有一个测试没通过就会被舍弃,之前为这个片元做的一切工作都会白费。只有通过测试的片元才有资格和颜色缓冲区合并。

书中给出了模板测试和深度测试的简化流程图:
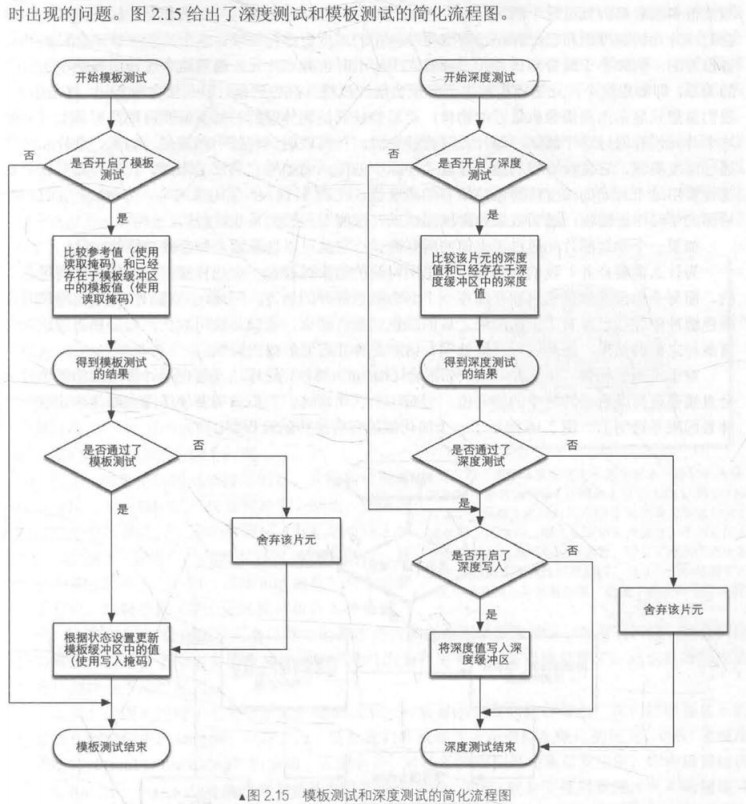
片元所需要经历的模板测试和深度测试这两大测试,都是可以由开发者自行配置的。在模板测试中,GPU首先读取(使用读取掩码)模板缓冲区中该片元位置的模板之,然后将该值与参考值(也使用读取掩码读取)进行比较判断是否舍弃(舍弃条件可以是小于或者大于等于)。然后根据模板测试和深度测试结果来修改模板缓冲区。这个修改操作也是由开发者指定的,模板测试通常用于限制渲染的区域,另外还有例如渲染阴影,轮廓渲染等高级用法。
如果片元通过模板测试,那么还会进行深度测试。这个测试同样是高度可配置的,GPU会将片元的深度值与深度缓冲区的深度值进行比较。比较舍弃和上述模板测试一样可以定义,通常是小于等于保留,大于等于舍弃。因为我们想渲染离摄像机更近,深度更低的物体。与模板测试不同的是,模板测试在保留或舍弃时都可以修改模板缓冲区,但是如果一个片元没有通过深度测试,它没有权利更改深度缓冲区的值,如果它通过了测试,开发者可以指定是否用这个片元的深度值覆盖掉原有片元的深度值,这是通过开启/关闭深度写入做到的。透明效果和深度测试以及深度写入的关系非常密切。
最后这些片元需要被合并。现在模板缓冲区已经修改了,深度缓冲区也进行了对应操作。其实所谓的渲染过程是一个物体一个物体地画到屏幕上的,因此我们还需要对像素颜色进行处理,而每个像素的颜色信息都被存储在一个名为颜色缓冲区的地方。当我们执行完这次渲染后,相同位置的颜色缓冲已经有了上次处理的结果,那么这次是直接覆盖?还是其它操作?这就是合并需要解决的问题。
例如对于不透明的物体,我们可以关闭混合(Blend) 操作,让颜色直接覆盖颜色缓冲。而对于半透明物体,我们需要混合颜色像素让其看起来像是透明的。
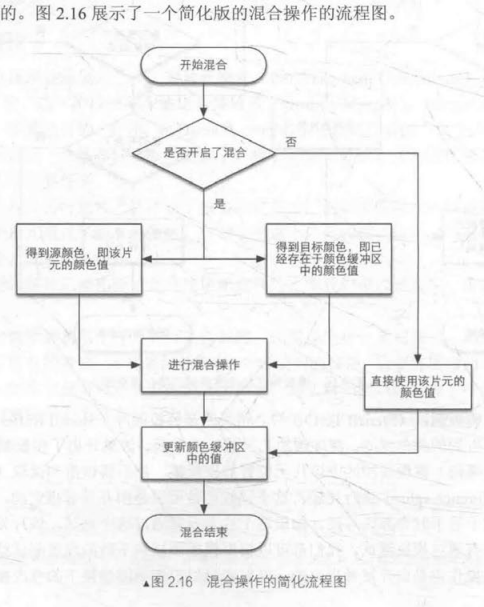
混合操作也是高度可配置的,我们可以选择是否开启混合,如果开启混合,GPU就会去除源颜色和目标颜色,源颜色指的是片元着色器得到的颜色值,而目标颜色是已经存在于颜色缓冲区的颜色值。之后使用一个混合函数来进行混合操作,这个混合函数与透明通道息息相关,例如根据透明通道的值进行相加、相减、相乘等。
那么我们就有疑问了,既然有的片元会在测试阶段被舍弃,这样不是很浪费吗?那么为什么不先进行测试再进行渲染呢?这样不是可以提高性能吗?就像下图的例子一样:

(上图先渲染球再渲染长方体,但是由于球先被渲染且深度更低,因此长方体大部分片元无法通过深度测试,对这些片元执行片元着色器造成了很大的性能浪费)
提前进行测试当然是可以的,例如文中就提到了可以提前进行深度测试的技术(Early-Z)。但是如果将测试提前的话,其检验结果可能与片元着色器中的一些操作冲突。例如,如果片元着色器中的代码进行了透明度测试,而片元没能通过,那么它将在着色器中被调用API(例如clip函数)被手动舍弃。这就导致GPU无法提前进行各种测试。因此,现代的GPU会判断片元着色器中的操作是否和提前测试冲突了,如果有冲突就会禁用提前测试。这样反而导致性能下降了,本来可以提前测试,由于添加了透明度测试反而不能提前测试了。
最终图元被渲染完成后会被呈现在屏幕上,我们的屏幕显示的就是颜色缓冲区中的颜色值。但是,为了避免我们看到那些正在进行光栅化的图元,GPU会使用双重缓冲(Double Buffering) 的策略,这意味着,对场景的渲染是在幕后发生的,即在后置缓冲(Back Buffer) 中。一旦场景被渲染到了后置缓冲中,GPU就会交换后置缓冲区和前置缓冲(Front Buffer) 中的内容。而前置缓冲区是之前显示在屏幕上的图像。因此保证了我们看到的图像总是连续的。(巧妙的方法,避免了渲染导致的画面不连续问题)
总结
虽然上述流程描述了很多(其实曲面细分着色器和几何着色器都没讲),但实际过程要更加复杂。当然上述内容与其他资料会产生差异,这是由于图像编程接口的实现不尽相同,而GPU在底层也做了很多优化。基本原理都是融会贯通的,未来可在学习Games101或者RTR4时重拾。
在Unity中为我们封装了很多功能,更多时候我们只需要在一个Unity Shader设置一些输入,编写顶点着色器和片元着色器,设置一些状态就能达到大部分常见的屏幕效果。(更别说现在Unity提供了URP和SRP等渲染管线)
虽然概念生疏,但是坚持才是胜利。无论经历了什么,选择了什么,既然选择了从事这个行业,那么都应该贯彻到底。勉励自己,也勉励诸位。
相关文章:

【UnityShader入门精要学习笔记】(2)GPU流水线
本系列为作者学习UnityShader入门精要而作的笔记,内容将包括: 书本中句子照抄 个人批注项目源码一堆新手会犯的错误潜在的太监断更,有始无终 总之适用于同样开始学习Shader的同学们进行有取舍的参考。 文章目录 上节复习GPU流水线顶点着色…...

CSS免费在线字体格式转换器 CSS @font-face 生成器
今天竟意外发现的一款免费的“网页字体生成器”,功能强大又好用~ 工具地址:https://transfonter.org/ 根据你设置生成后的文件预览: 支持TTF、OTF、WOFF、WOFF2 或 SVG字体格式转换生成,每个文件最大15MB。转换完成以后还会生成一…...
Codeium在IDEA里的3个坑
转载自Codeium在IDEA里的3个坑:无法log in,downloading language server和中文乱码_downloading codeium language server...-CSDN博客文章浏览阅读1.7w次,点赞26次,收藏47次。Codeium安装IDEA插件的3个常见坑_downloading codeiu…...

C-C++ 项目构建指南:如何使用 Makefile 提高开发效率
Makefile是一个常用的自动化构建工具,它可以为开发人员提供方便的项目构建方式。在C/C项目中,Makefile可以用来编译、链接和生成可执行文件。使用Makefile的好处是可以自动执行一系列命令,从而减少手动操作的复杂性和出错的可能性。此外&…...

基于SpringBoot的图书管理系统
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 🚀🚀🚀SpringBoot 阿博图书管理系…...

矩阵对角线遍历
Diagonal 2614. 对角线上的质数 class Solution {public int diagonalPrime(int[][] nums) {int n = nums....
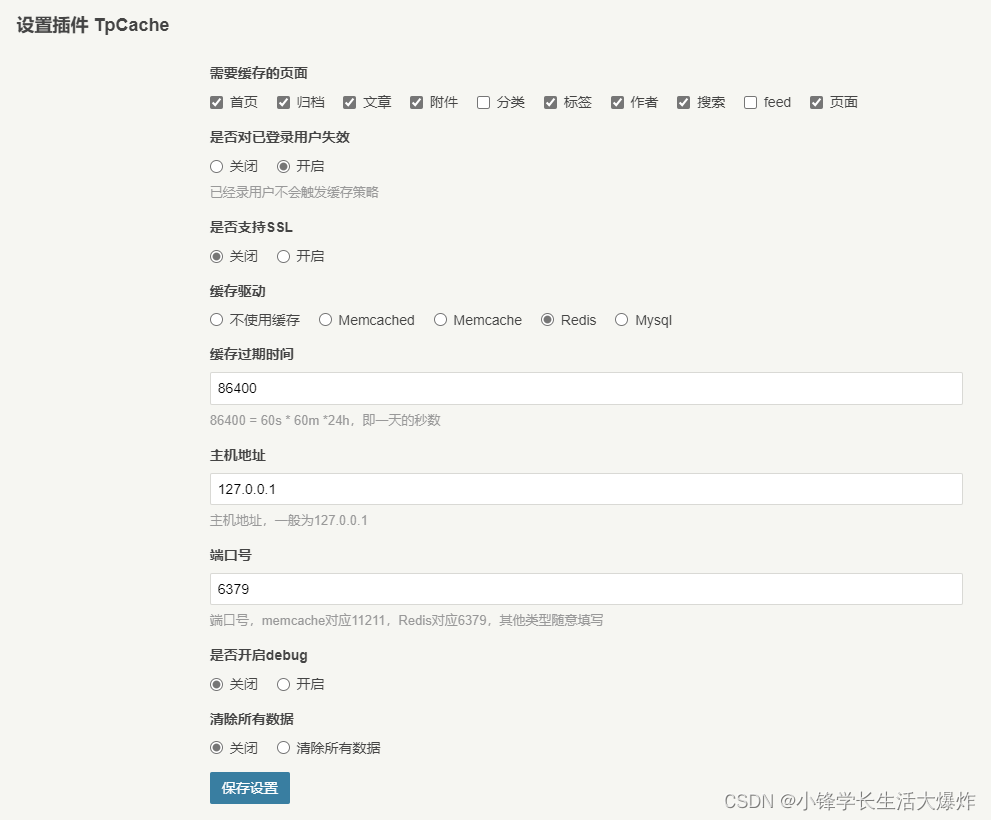
【教程】Typecho Joe主题开启并修复壁纸相册不显示问题
转载请注明出处:小锋学长生活大爆炸[xfxuezhang.cn] 背景说明 Joe主题本身支持“壁纸”功能,其实就是相册。当时还在网上找了好久相册部署的开源项目,太傻了。 但是网上教程很少,一没说如何开启壁纸功能,二没说开启后为…...

MR混合现实情景实训教学系统在法律专业课堂上的应用
MR混合现实情景实训教学系统是一种将虚拟现实(VR)、增强现实(AR)相结合的先进技术。在法律教学课堂上,MR教学系统为学生模拟模拟法庭、案例分析等多种形式,让学生在实践中掌握法律知识,提高法律…...

车载 Android之 核心服务 - CarPropertyService 的VehicleHAL
前言: 本文是车载Android之核心服务-CarPropertyService的第二篇,了解一下CarPropertyService的VehicleHAL, 第一篇在车载 Android之 核心服务 - CarPropertyService 解析-CSDN博客,有兴趣的 朋友可以去看下。 本节介绍 AndroidAutomotiveOS中对于 Veh…...

年底了,准备跳槽的可以看看...
前两天跟朋友感慨,今年的铜九铁十、裁员、疫情导致好多人都没拿到offer!现在已经1月了,具体明年的金三银四只剩下两个月。 对于想跳槽的职场人来说,绝对要从现在开始做准备了。这时候,很多高薪技术岗、管理岗的缺口和市场需求也出…...

Bagging算法_随机森林Random_Forest
Bagging B a g g i n g Bagging Bagging是并行式集成学习方法最著名的代表,这个名字是由 B o o t s t r a p A G G r e g a t I N G Bootstrap AGGregatING BootstrapAGGregatING而来,顾名思义,该算法由 B o o s t s t r a p Booststrap Boos…...
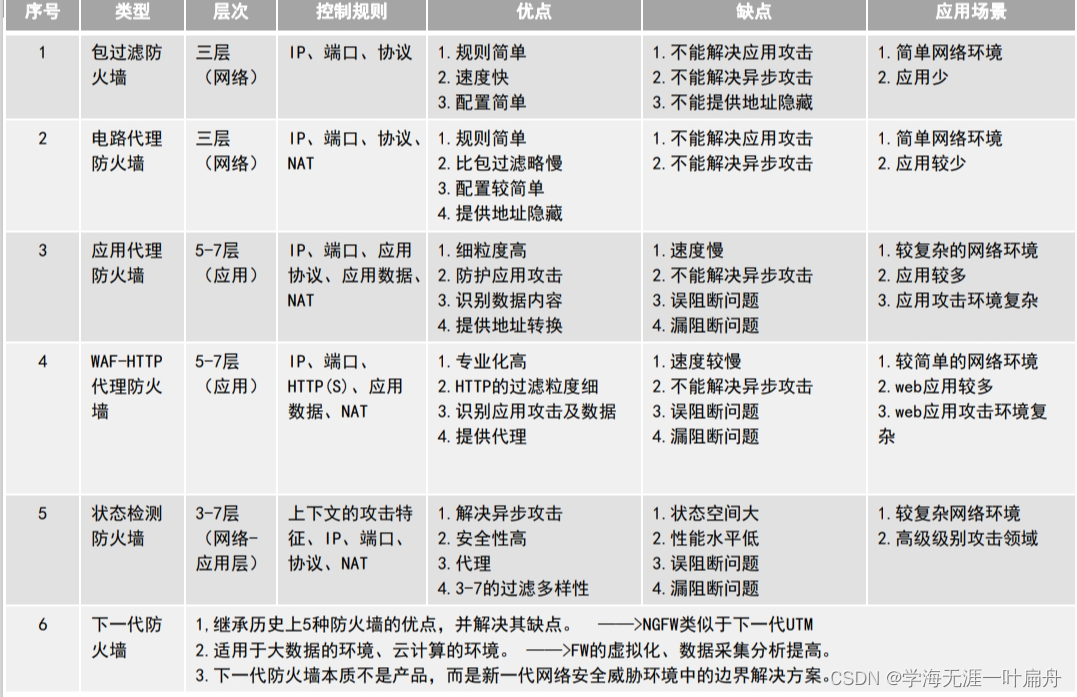
物理与网络安全
物流环境安全 场地选择考虑抗震、承重、防火、防水、供电、空气调节、电磁防护、雷击及静电 场地因素: 自然灾害,社会因素(加油站、化工厂),配套条件(消防,交通,电力,…...
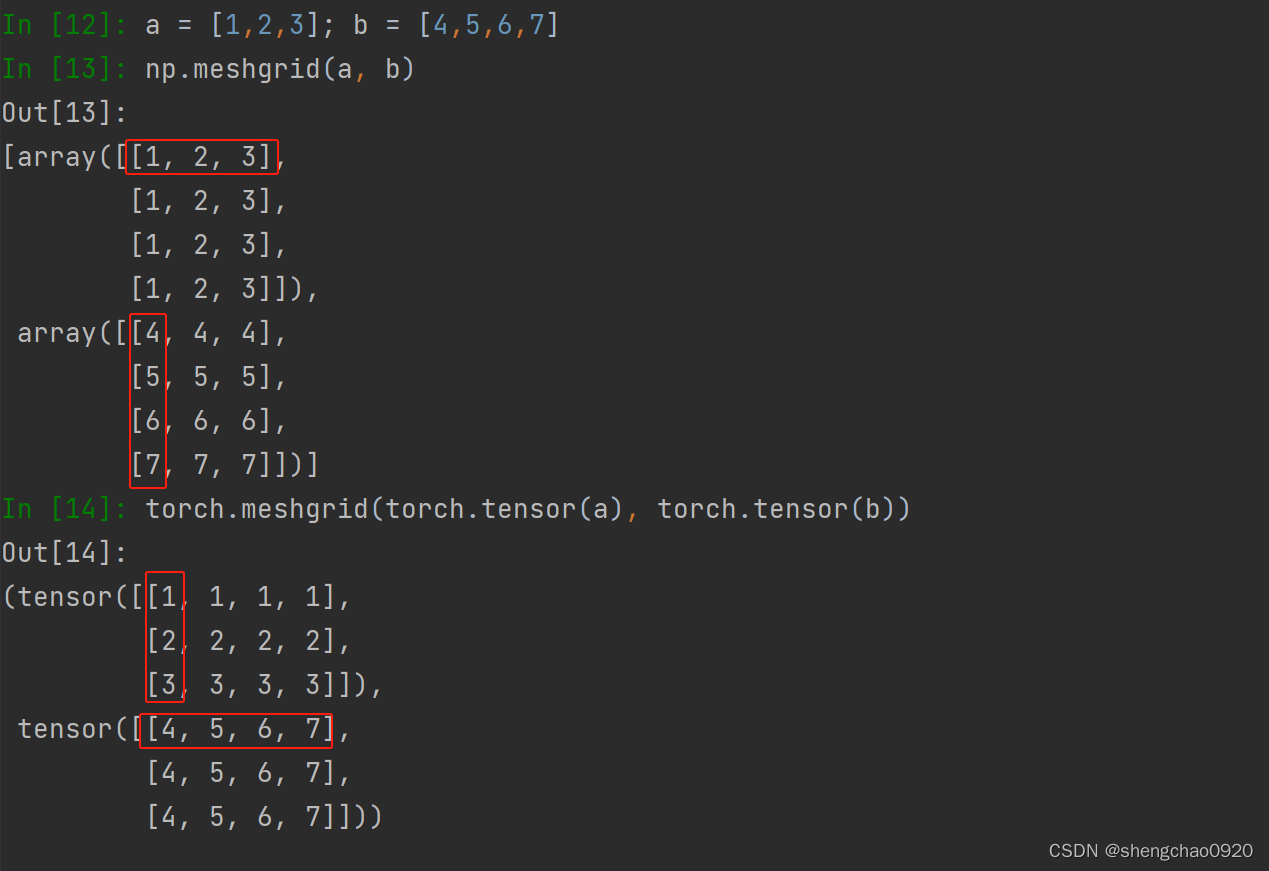
torch.meshgrid和np.meshgrid的区别
numpy中meshgrid: 把数组a当作一行,再根据数组b的长度扩充行。 把数组b当作一列,再根据数组a的长度扩充列。 torch中meshgrid: 把数组a当作一列,再根据数组b的长度扩充列。 把数组b当作一行,再根据数组a的…...

【PostgreSQL】约束-唯一约束
【PostgreSQL】约束链接 检查 唯一 主键 外键 排他 唯一约束 唯一约束是数据库中的一种约束,用于确保某个列或字段的值在该列或字段中是唯一的。唯一约束可用于确保数据库表中的某个列中的值是唯一的,也可用于确保多个列的组合值是唯一的。 在创建表…...

学习使用js/jquery获取指定class名称的三种方式
学习使用js/jquery获取指定class名称的三种方式 简介一、获取元素的class名称1、通过原生JS获取元素的class名称2、通过Jquery获取元素的class名称 二、应用1、样式修改2、动画效果实现 简介 在开发网页时,我们经常需要通过JS获取元素的class名称进行一些操作&…...

latex数学公式
写于:2024年1月5日 晚 修改: 摘要:数学公式根据其位置可以分为行内公式和行间公式。行内公式更加紧凑,而行间公式富于变化,可以为其编号、引用、换行等操作。本文对数学公式的 LaTex 做简单记录和整理。 行内公式 行内…...

frp配置内网穿透访问家里的nas
frp配置内网穿透访问家里的nas 需求 家里局域网内有台nas,在去公司的路上想访问它 其内网地址为: http://192.168.50.8:6002 工具 1.frp版本v0.53.2 下载地址: https://github.com/fatedier/frp/releases/download/v0.53.2/frp_0.53.2_li…...

C语言-蓝桥杯2023年第十四届省赛真题-砍树
题目描述 给定一棵由 n 个结点组成的树以及 m 个不重复的无序数对 (a1, b1), (a2, b2), . . . , (am, bm),其中 ai 互不相同,bi 互不相同,ai ≠ bj(1 ≤ i, j ≤ m)。 小明想知道是否能够选择一条树上的边砍断,使得对于每个 (a…...
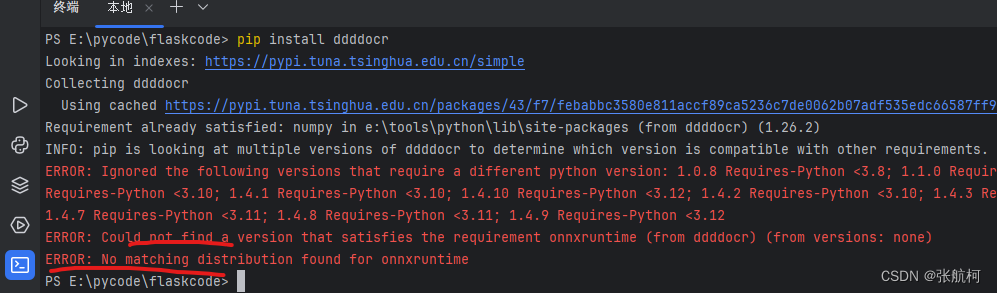
python识别验证码+灰度图片base64转换图片
一、为后面识别验证码准备 1、base64转换为图片,保存本地、并且置灰 上文中的base64,后面的就是包含Base64编码的PNG图像的字符串复制下来 import base64 from PIL import Image import io# 这里是你的Base64编码的字符串 base64_data "iVBORw0KGgoAAAANSUhE…...
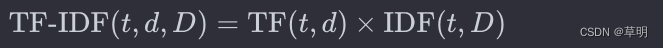
TF-IDF(Term Frequency-Inverse Document Frequency)算法 简介
TF-IDF(Term Frequency-Inverse Document Frequency)是一种用于信息检索和文本挖掘的常用算法。它用于评估一个词对于一个文档集合中某个文档的重要性。 这个算法的基本思想是:如果一个词在一个文档中频繁出现,并且在整个文档集合…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...
