VUE--保留小数(过滤器)
1.cutOutNum.js
export const cutOutNum = (num, decimals) => {if (isNaN(num) || (!num && num !== 0)) {return "-";}function toNonExponential(_num) {var m = Number(_num).toExponential().match(/\d(?:\.(\d*))?e([+-]\d+)/);return Number(_num).toFixed(Math.max(0, (m[1] || "").length - m[2]));}// 为了兼容科学计数法的数字num = toNonExponential(num);// 获取小数点的位置 + 1(不存在小数点的indexOf值为-1)const pointIndex = String(num).indexOf(".") + 1;// 获取小数点后的个数(需要保证有小数位)const pointCount = pointIndex ? String(num).length - pointIndex : 0;// 补零函数function zeroFill(zeroNum, num) {for (let index = 0; index < zeroNum; index++) {num = `${num}0`;}return num;}// 源数据为"整数"或者小数点后面小于decimals位的作补零处理if (pointIndex === 0 || pointCount <= decimals) {let tempNumA = num;// 区分"整数"和"小数"的补零if (pointIndex === 0) {tempNumA = `${tempNumA}.`;tempNumA = zeroFill(decimals - pointCount, tempNumA);} else {tempNumA = zeroFill(decimals - pointCount, tempNumA);}return Number(tempNumA) === 0 ? 0 : tempNumA;}// 截取当前数据到小数点后decimals位const Int = String(num).split(".")[0];const Decimal = String(num).split(".")[1].substring(0, decimals);const tempNumB = `${Int}.${Decimal}`;// 需求:数据为0时,需要显示为0,而不是0.00...return tempNumB;
};2.调用
<template><div>{{ total | numFilter }}</div>
</template><script>
import { cutOutNum } from "@/util/cutOutNum";
export default {data() {return {total: 2.3334,};},filters: {numFilter(value) {return cutOutNum(value, 3);},},methods: {},
};
</script><style>
</style>
相关文章:
)
VUE--保留小数(过滤器)
1.cutOutNum.js export const cutOutNum (num, decimals) > {if (isNaN(num) || (!num && num ! 0)) {return "-";}function toNonExponential(_num) {var m Number(_num).toExponential().match(/\d(?:\.(\d*))?e([-]\d)/);return Number(_num).toF…...
书生·浦语大模型实战营第一次课堂笔记
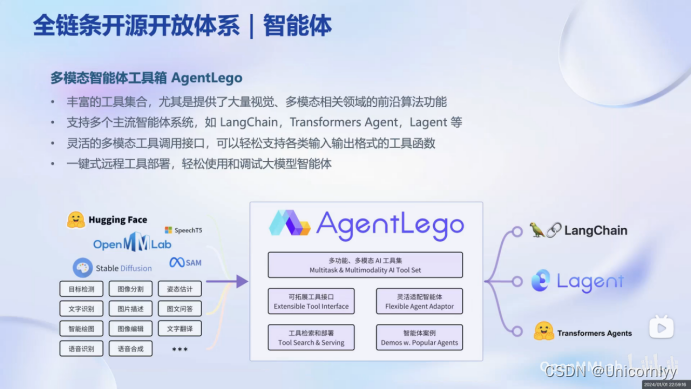
书生浦语大模型全链路开源体系。大模型是发展通用人工智能的重要途径,是人工通用人工智能的一个重要途径。书生浦语大模型覆盖轻量级、重量级、重量级的三种不同大小模型,可用于智能客服、个人助手等领域。还介绍了书生浦语大模型的性能在多个数据集上全面超过了相似量级或相近…...
Mysql为什么只能支持2000w左右的数据量?
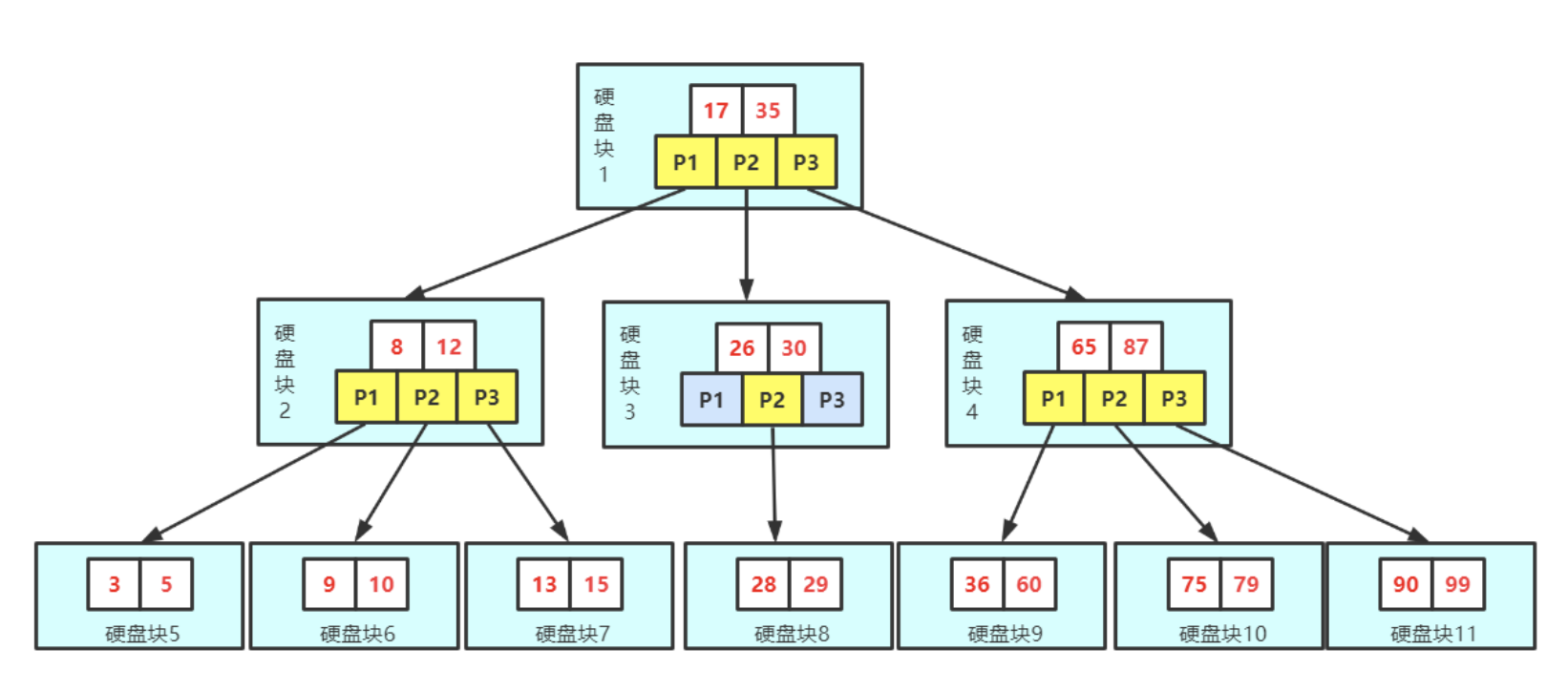
首先说明一下: MySQL并没有硬性规定只能支持到2000万左右的数据量。 其实,MySQL能够处理的数据量远远超过这个数字。无论是开源社区版还是商业版, MySQL在适当的硬件和配置下,都能够支持非常大的数据集。 通常所说的“MySQL只能…...
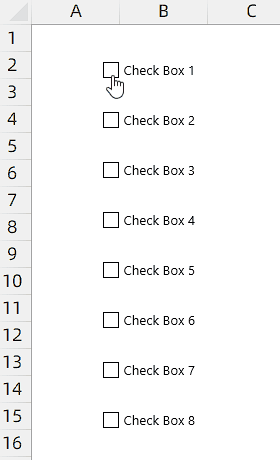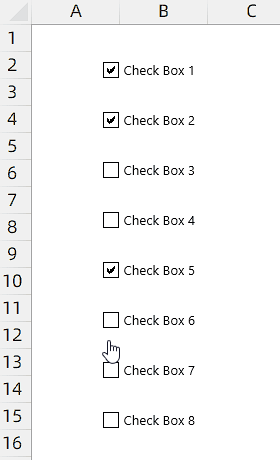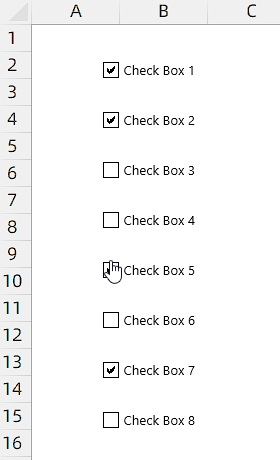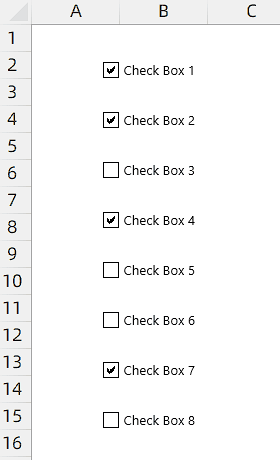
限制选中指定个数CheckBox控件(1/2)
限制选中指定个数CheckBox控件(1/2) 实例需求:工作表中有8个CheckBox控件(下文中简称为控件),现在需要实现限制用户最多只能勾选4个控件。 Dim OnDic As Object Sub CheckboxeEvent()Dim oCB As CheckBox…...
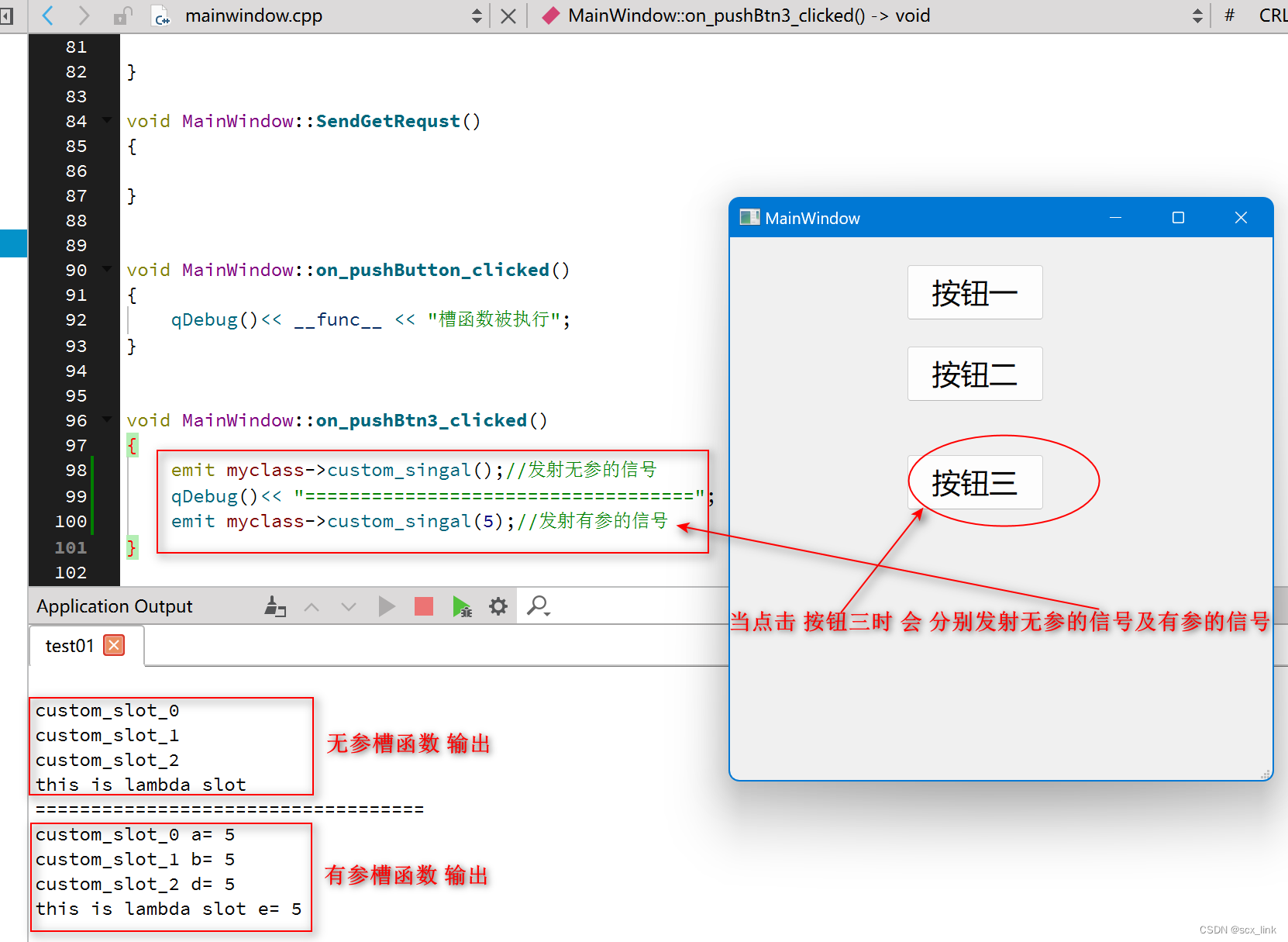
QT中的信号与槽的讲解
文章目录 信号及其特点槽及其特点代码演示标准信号与标准槽函数方式一方式二 自定义信号和槽connect()函数信号和槽函数存在函数重载的情况下Qt的信号槽机制注意事项 信号及其特点 信号:是一种特殊的函数,又称信号函数,俗称信号,…...

RNN文本分类任务实战
递归神经网络 (RNN): 定义:RNN 是一类专为顺序数据处理而设计的人工神经网络。 顺序处理:RNN 保持一个隐藏状态,该状态捕获有关序列中先前输入的信息,使其适用于涉及顺序依赖关系的任务。词嵌入…...

【算法系列 | 12】深入解析查找算法之—斐波那契查找
序言 心若有阳光,你便会看见这个世界有那么多美好值得期待和向往。 决定开一个算法专栏,希望能帮助大家很好的了解算法。主要深入解析每个算法,从概念到示例。 我们一起努力,成为更好的自己! 今天第12讲,讲…...

全新的C++语言
一、概述 C 的最初目标就是成为 “更好的 C”,因此新的标准首先要对基本的底层编程进行强化,能够反映当前计算机软硬件系统的最新发展和变化(例如多线程)。另一方面,C对多线程范式的支持增加了语言的复杂度࿰…...

three.js 多通道组合
效果: 代码: <template><div><el-container><el-main><div class"box-card-left"><div id"threejs" style"border: 1px solid red"></div><div style"border: 1px so…...

编程笔记 html5cssjs 022 HTML表单概要
编程笔记 html5&css&js 022 HTML表单概要 一、<form> 元素二、HTML Form 属性三、操作小结 网页光是输出没有输入可不行,因为输出还是比输入容易,所有就先接触输出,后学习输入。html用来输入的东西叫“表单”。 HTML 表单用于搜…...

三子棋(c语言)
前言: 三子棋是一种民间传统游戏,又叫九宫棋、圈圈叉叉棋、一条龙、井字棋等。游戏规则是双方对战,双方依次在9宫格棋盘上摆放棋子,率先将自己的三个棋子走成一条线就视为胜利。但因棋盘太小,三子棋在很多时候会出现和…...
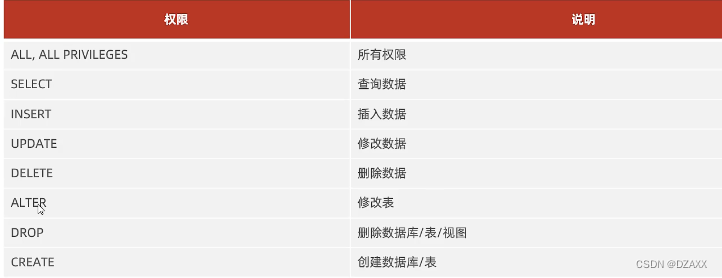
MySQL-DCL
DCL是数据控制语言,用来管理数据库用户,控制数据库的访问权限。 管理用户:管理哪些用户可以访问哪些数据库 1.查询用户 USE mysql; SELECT * FROM user; 注意: MySQL中用户信息和用户的权限信息都是记录在mysql数据库的user表中的…...

QT开源类库集合
QT开源类库集合 一、自定义控件 QSintQicsTableLongscroll-qtAdvanced Docking System 二、图表控件 QwtQCustomPlotJKQTPlotter 三、网络 QHttpEngineHTTP 四、 音视频 vlc-qt 五、多线程 tasks 六、数据库 EasyQtSql 一、自定义控件 1. QSint 源代码地址:QSint&…...
--算法(2))
C++ STL(2)--算法(2)
算法(2)----STL里的排序函数。 1. sort: 对容器或普通数组中指定范围内的元素进行排序,默认进行升序排序。 sort函数是基于快速排序实现的,属于不稳定排序。 只支持3种容器:array、vector、deque。 如果容器中存储的是自定义的对象ÿ…...
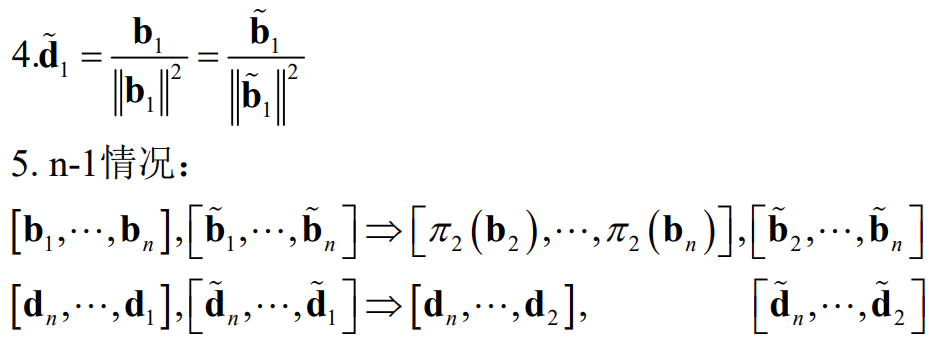
格密码基础:对偶格(超全面)
目录 一. 对偶格的格点 1.1 基本定义 1.2 对偶格的例子 1.3 对偶格的图形理解 二. 对偶格的格基 2.1 基本定义 2.2 对偶格的格基证明 三. 对偶格的行列式 3.1 满秩格 3.2 非满秩格 四. 重复对偶格 五. 对偶格的转移定理(transference theoremÿ…...

ECMAScript简介及特性
ECMAScript是一种由ECMA国际(前身为欧洲计算机制造商协会)制定和发布的脚本语言规范,JavaScript在它基础上进行了自己的封装。ECMAScript和JavaScript的关系是,前者是后者的规格,后者是前者的一种实现。 ECMAScript的…...
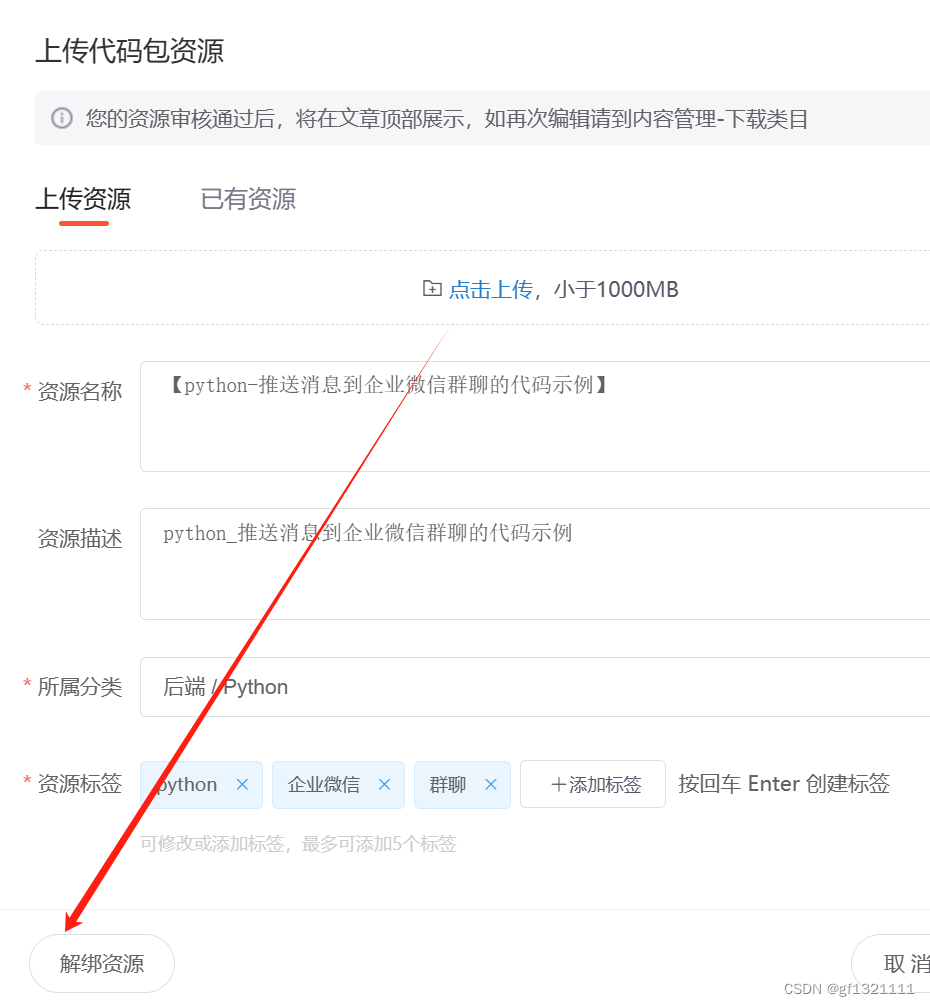
csdn中的资源文件如何删除?
csdn中的资源文件如何删除? 然后写文章的时候 点击资源绑定,解锁资源,就可以再次上传。...

NA原理及配置
在IP地址空间中,a;b;c类地址中各有一部分地址,被称为私有IP地址(私网地址),其余的为公有IP地址(公网地址) A:10.0.0.0 - 10.255.255.255 --- 相当于1条A类网段…...

解决:TypeError: ‘tuple’ object does not support item assignment
解决:TypeError: ‘tuple’ object does not support item assignment 文章目录 解决:TypeError: tuple object does not support item assignment背景报错问题报错翻译报错位置代码报错原因解决方法方法一:方法二:今天的分享就到…...
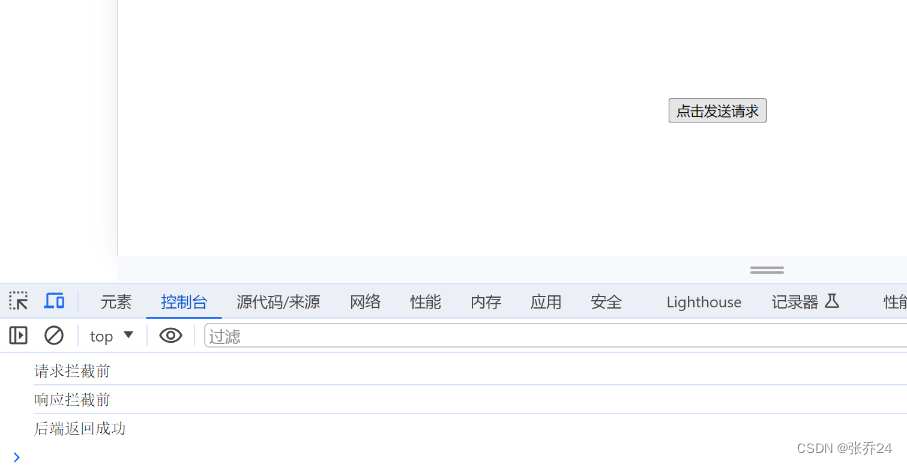
vue3项目中axios的常见用法和封装拦截(详细解释)
1、axios的简单介绍 Axios是一个基于Promise的HTTP客户端库,用于浏览器和Node.js环境中发送HTTP请求。它提供了一种简单、易用且功能丰富的方式来与后端服务器进行通信。能够发送常见的HTTP请求,并获得服务端返回的数据。 此外,Axios还提供…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
