盖子的c++小课堂——第二十三讲:背包问题
前言
又是一次漫长的更新(我真不是故意的aaaaaaaaaaaaaaa),先不多说了,直接给我~坐下~说错了说错了,直接开始~
背包问题----动态规划
背包问题(knapsack problem)
动态规划(dynamic programming)
01背包:可行性
对一个背包最多载重m斤,共有n件物品,第i件物品重量为w[i]。对每件物品可选择拿走或不拿。请问能否恰好拿到总重量为m斤?

01决策:不选0,选1
凑数:可行性
目标凑出数字m,有n个数字可以使用,第i个数字为x[i]。对每一个数字最多可以选用1次。请问能否恰好凑出数字m?

01决策:不选0,选1
简化问题

01背包:可行性
f[i][j]表示只用前i个数字能否凑出j
初始条件
f[0][0]=1
状态转移方程
若j<x[i]——f[i][j]=f[i-1][j]
若j>=x[i]——f[i][j]=f[i-1][j]或f[i-1][j-x[i]]
01背包:3种问题
可行性判定问题
用n个物品能否恰好凑出m斤重量
方案计数问题
用n个物品能否恰好凑出m斤各种方案
最优化问题
用n个物品凑出不超过m斤时最多几斤
01背包
关于01背包,建议结合我的B站视频一起学习,相信会对你彻底理解背包问题有很大帮助!
带你学透0-1背包问题!| 关于背包问题,你不清楚的地方,这里都讲了!| 动态规划经典问题 | 数据结构与算法_哔哩哔哩_bilibiliwww.bilibili.com/video/BV1cg411g7Y6编辑![]() https://link.zhihu.com/?target=https%3A//www.bilibili.com/video/BV1cg411g7Y6带你学透01背包问题(滚动数组篇) | 从此对背包问题不再迷茫!_哔哩哔哩_bilibiliwww.bilibili.com/video/BV1BU4y177kY编辑
https://link.zhihu.com/?target=https%3A//www.bilibili.com/video/BV1cg411g7Y6带你学透01背包问题(滚动数组篇) | 从此对背包问题不再迷茫!_哔哩哔哩_bilibiliwww.bilibili.com/video/BV1BU4y177kY编辑![]() https://link.zhihu.com/?target=https%3A//www.bilibili.com/video/BV1BU4y177kY
https://link.zhihu.com/?target=https%3A//www.bilibili.com/video/BV1BU4y177kY
有N件物品和一个最多能被重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。

这是标准的背包问题,以至于很多混丝看了这个自然就会想到背包,甚至都不知道暴力的解法应该怎么解了。
这样其实是没有从底向上去思考,而是习惯性想到了背包,那么暴力的解法应该是怎么样的呢?
每一件物品其实只有两个状态,取或者不取,所以可以使用回溯法搜索出所有的情况,那么时间复杂度就是O(2^n),这里的n表示物品数量。
二维dp数组01背包
确定dp数组以及下标的含义
对于背包问题,有一种写法, 是使用二维数组,即dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少?
要时刻记着这个dp数组的含义,下面的一些步骤都围绕这dp数组的含义进行的,如果哪里看懵了,就来回顾一下i代表什么,j又代表什么。
确定递推公式
再回顾一下dp[i][j]的含义:从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
那么可以有两个方向推出来dp[i][j],
- 由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]
- 由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
dp数组如何初始化
关于初始化,一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱。
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。
状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
代码如下:
for (int j = weight[0]; j <= bagWeight; j++) {dp[0][j] = value[0];
}dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化多少呢?
dp[i][j]在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了,因为0就是最小的了,不会影响取最大价值的结果。
如果题目给的价值有负数,那么非0下标就要初始化为负无穷了。例如:一个物品的价值是-2,但对应的位置依然初始化为0,那么取最大值的时候,就会取0而不是-2了,所以要初始化为负无穷。
而背包问题的物品价值都是正整数,所以初始化为0,就可以了。
这样才能让dp数组在递归公式的过程中取最大的价值,而不是被初始值覆盖了。
最后初始化代码如下:
vector<vector<int>> dp(weight.size() + 1, vector<int>(bagWeight + 1, 0));
for (int j = weight[0]; j <= bagWeight; j++) {dp[0][j] = value[0];
}那么问题来了,先遍历物品还是先遍历背包重量呢?
其实都可以!! 但是先遍历物品更好理解。
那么我先给出先遍历物品,然后遍历背包重量的代码。
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量if (j < weight[i]) dp[i][j] = dp[i - 1][j]; // 这个是为了展现dp数组里元素的变化else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}
}先遍历背包,再遍历物品,也是可以的
例如这样:
// weight数组的大小 就是物品个数
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量for(int i = 1; i < weight.size(); i++) { // 遍历物品if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}
}为什么也是可以的呢?
要理解递归的本质和递推的方向。
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的。
dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括正左和正上两个方向)
其实背包问题里,两个for循环的先后循序是非常有讲究的,理解遍历顺序其实比理解推导公式难多了。
总结
讲了这么多才刚刚把二维dp的01背包讲完,这里大家其实可以发现最简单的是推导公式了,推导公式估计看一遍就记下来了,但难就难在如何初始化和遍历顺序上。
可能有的混丝并没有注意到初始化和遍历顺序的重要性,我们后面做力扣上背包面试题目的时候,大家就会感受出来了。
(这真是n年一度的大更新)
相关文章:

盖子的c++小课堂——第二十三讲:背包问题
前言 又是一次漫长的更新(我真不是故意的aaaaaaaaaaaaaaa),先不多说了,直接给我~坐下~说错了说错了,直接开始~ 背包问题----动态规划 背包问题(knapsack problem) 动态规划(dyna…...

k8s安装hostPath方式存储的PostgreSQL15
1.配置 PostgreSQL 的 ConfigMap cat > postgres-configmap.yaml << EOF apiVersion: v1 kind: ConfigMap metadata:name: postgres-configlabels:app: postgresnamespace: dev data:POSTGRES_DB: postgresdbPOSTGRES_USER: postgresadminPOSTGRES_PASSWORD: admin12…...
51单片机之按键和数码管
51单片机之按键和数码管 ✍前言:♐独立按键😀独立按键的原理😀软件实现按键控制LED灯的亮灭 ♐数码管😊数码管显示数字或者字母的原理🐉共阳极数码管🐉共阴极极数码管🐉4位1体数码管 Ƕ…...

【Oracle】 - 数据库的实例、表空间、用户、表之间关系
Oracle是一种广泛使用的关系型数据库管理系统,它具有高性能、高可靠性、高安全性等特点。1Oracle数据库的结构和组成是一个复杂而又有趣的话题,本文将介绍Oracle数据库的四个基本概念:数据库、实例、表空间和用户,以及它们之间的关…...
ssm基于HTML5的交流论坛的设计与实现+vue论文
摘 要 信息数据从传统到当代,是一直在变革当中,突如其来的互联网让传统的信息管理看到了革命性的曙光,因为传统信息管理从时效性,还是安全性,还是可操作性等各个方面来讲,遇到了互联网时代才发现能补上自古…...

JDBC*
*JDBC数据库连接步骤 1.将JDBC驱动的jar添加到项目的依赖中。 2.加载JDBC驱动 例如: Class.forName("com.mysql.jdbc.Driver"); 3.连接数据库 例如: Connection con DriverManager.getConnection(URL,us…...

Zookeeper注册中心实战
Java学习手册面试指南:https://javaxiaobear.cn Spring Cloud Zookeeper通过自动配置和绑定到 Spring 环境和其他 Spring 编程模型习惯用法,为 Spring Boot 应用程序提供Apache Zookeeper集成。通过一些简单的注释,您可以快速启用和配置应用…...
1-02VS的安装与测试
一、概述 对于一名C语言程序员而言,进行C语言程序的开发一般需要一个文本编辑器加上一个编译器就足够了。但为了方便起见,我们选择使用集成开发环境——Visual Studio(简称VS)。安装Visual Studio 下面讲一下如何安装VS࿰…...
ctfshow——PHP特性
文章目录 web 89web 90web 91web 92web 93web 94web 95web 96web 97web 98web 99web 100——优先级、eval()用法web 101——RefelctionClass反射类web 102——php伪协议、hex2bin()web103web 104——sha1绕过web 105 web 89 使用人工分配 ID 键的数值型数组绕过preg_match. 两个…...

K8S陈述式资源管理
陈述式 命令行:kubectl命令行工具 优点:90%以上的场景都可以满足,对增,删,查比较方便,对改不是很友好 缺点:命令比较冗长,复杂,难记 声明式 k8s当中的yaml文件来实现资…...

详解Python内置函数 !!!
内置函数就是Python给你提供的, 拿来直接用的函数,比如print,input等。 文章目录 前言 一、和数字相关 1. 数据类型 2. 进制转换 3. 数学运算 二、和数据结构相关 1. 序列 2. 数据集合 3. 相关内置函数 三、和数据结构相关 四、和迭代器生成器相关 五、字…...
)
使用Vue3 + Vite创建uni-app项目(Webstorm)
使用Vue3 Vite创建uni-app项目(Webstorm) 参考:前端VUE3Vite UniAPP-- 框架搭建_uniapp vite-CSDN博客 // 参考github.com的库:https://github.com/dcloudio/uni-preset-vue npx degit dcloudio/uni-preset-vue#vite-ts vite-vu…...
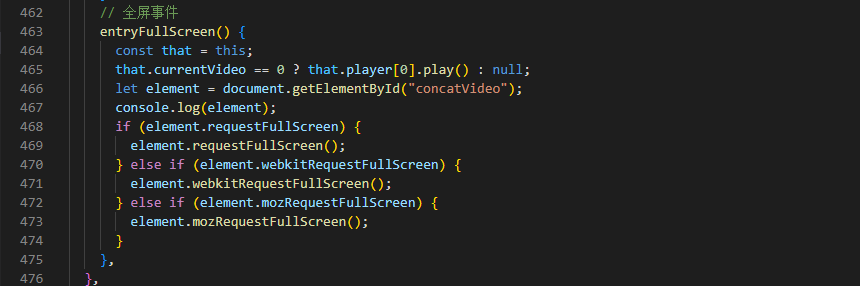
【js】js实现多个视频连续播放:
文章目录 一、效果:二、实现:三、案例: 一、效果: 二、实现: <!DOCTYPE html> <html> <head><title>Video Player</title><style>#progressBar { width: 800px;height: 20px;b…...
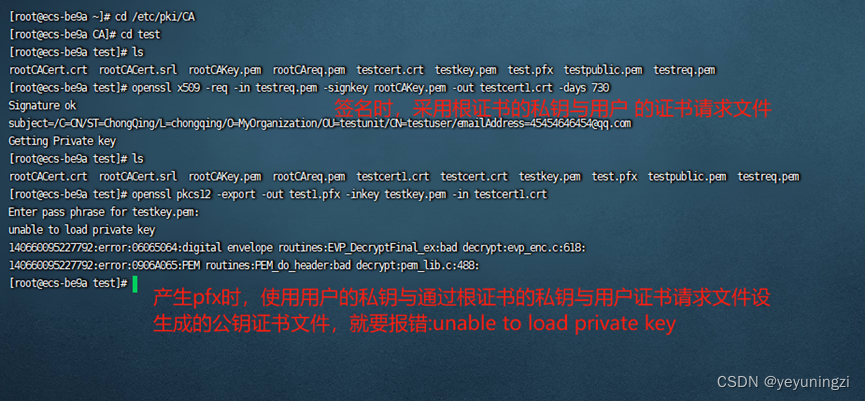
使用openssl 生成pfx格式证书时报错:unable to load certificates
问题现象包如下: 之前在centos上使用openssl部署证书服务器以及颁发证书的时候遇到的问题,在进行个人证书生成之后需要形成pfx格式证书,结果过程中报错了。网上类似资料比较少,做个记录。 生成pfx格式证书的命令: o…...

微信小程序 分享按钮 监听用户分享成功
代码 <view><button class"btnLq ed flex justify-center" open-type"share" click"getAward">点击分享</button> </view>export default {data(){return{shareMd:false,//分享埋点}},onShow(){//if(this.shareMd){uni.…...

数据结构-怀化学院期末题
题目: 利用希尔排序算法实现线性表的排序。希尔排序是根据给定的增量序列将线性表分隔成某个“增量”的记录组成一个子序例,在子序列中采用直接插入排序完成。 输入 第一行为元素个数n(1<n<1000),第二行为n个元素值(整数),即…...
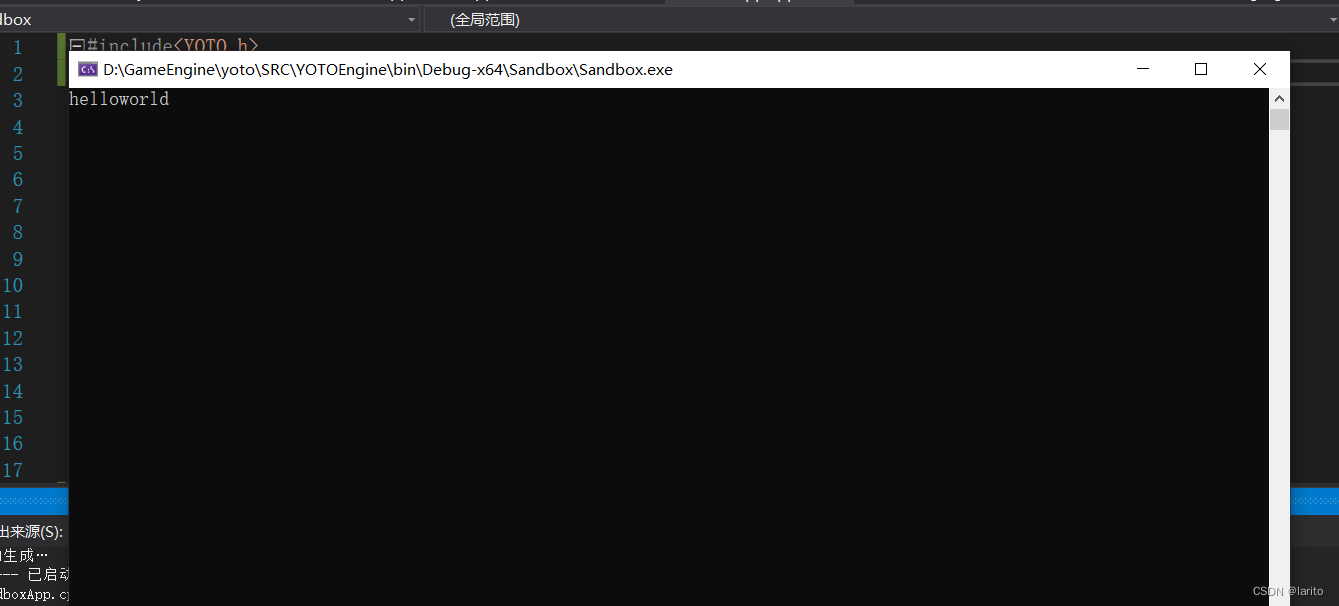
跟cherno手搓游戏引擎【1】:配置与入口点
环境配置: 编译环境:VS2019 创建两个项目: 设置Sandbox为启动项: 设置sandbox的配置属性-常规-输出目录\中间目录为如下: 预处理定义:为了配置一些只有windows才能用的函数。 设置YOTOEngin(我…...
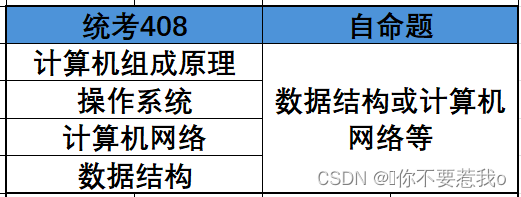
25计算机专业考研经验贴之准备篇
Hello各位小伙伴,大家新年好! 马上就要进入寒假假期了,25考研也该提上日程了。今天先跟大家分享一下大家在假期可以先做起来的准备工作。 【选择学校】 择校是个非常重要的内容,因为不同学校的考试内容是不一样的,有些…...
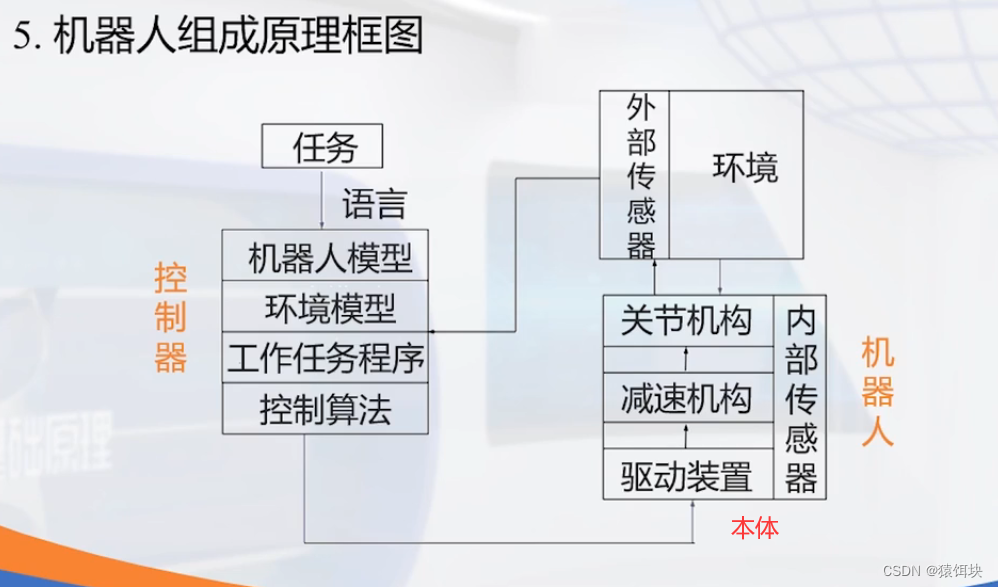
机器人相关知识
机器人学(Robotics) 一些基础概念 位姿 位姿位置姿态 位姿的表示 刚体 刚性物体是一组粒子的集合,其中任意两个粒子之间的距离保持固定,不受物体运动或施加在物体上的力的影响。 “完全不可变形”的物体就是刚体。 刚体位置 刚性连杆 …...
)
八股文打卡day22——操作系统(5)
面试题:什么是死锁?如何避免死锁? 我的回答: 死锁是两个或者多个进程都占有各自的资源,然后都互相请求资源,导致互相都陷入了阻塞状态。 如何避免死锁呢? 首先,造成死锁有四个必要…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
