AVL 树实现
AVL 树的概念
也许因为插入的值不够随机,也许因为经过某些插入或删除操作,二叉搜索树可能会失去平衡,甚至可能退化为单链表,造成搜索效率低。

AVL Tree 是一个「加上了额外平衡条件」的二叉搜索树,其平衡条件的建立是为了确保整棵树的深度为 O(log2N)O(log_2N)O(log2N)。
AVL Tree 要求任何节点的左右子树高度相差最多为 1。当违反该规定时,就需要进行旋转来保证该规定。
AVL 树的实现
节点的定义
AVL 树节点的定义比一般的二叉搜索树复杂,它需要额外一个 parent 指针,方便后续旋转。并在每个节点中引入平衡因子,便于判断是否需要旋转。
/// @brief AVL 树节点结构
/// @tparam K 节点的 key 值
/// @tparam V 节点的 value 值
template <class K, class V>
struct AVLTreeNode {AVLTreeNode(const pair<K, V>& kv) : _kv(kv), _parent(nullptr), _left(nullptr), _right(nullptr), _bf(0){}pair<K, V> _kv;AVLTreeNode<K, V>* _parent;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;// 左右子树高度相同平衡因子为:0// 左子树高平衡因子为负// 右子树高平衡因子为正int _bf;
};
接口总览
template<class K, class V>
class AVLTree {typedef AVLTreeNode<K, V> Node;
public:Node* Find(const K& key);bool Insert(const pair<K, V>& kv);private:void RotateR(Node* parent);void RotateL(Node* parent);void RotateLR(Node* parent);void RotateRL(Node* parent);
private:Node* _root = nullptr;
};
查找
AVL 树的查找和普通的搜索二叉树一样:
- 若 key 值大于当前节点的值,在当前节点的右子树中查找
- 若 key 值小于当前节点的值,在当前节点的左子树中查找
- 若 key 值等于当前节点的值,返回当前节点的地址
- 若找到空,查找失败,返回空指针
/// @brief 查找指定 key 值
/// @param key 要查找的 key
/// @return 找到返回节点的指针,没找到返回空指针
Node* Find(const K& key) {Node* cur = _root;while (cur != nullptr) {// key 值与当前节点值比较if (key > cur->_kv.first) {cur = cur->_right;} else if (key < cur->_kv.first) {cur = cur->_left;} else {return cur;}}return nullptr;
}
插入
AVL 的插入整体分为两步:
- 按照二叉搜索树的方式将节点插入
- 调整节点的平衡因子
平衡因子是怎么调整的?
设新插入的节点为 pCur,新插入节点的父节点为 pParent。在插入之前,pParent 的平衡因子有三种可能:0、-1、1。
插入分为两种:
- pCur 插入到 pParent 的左侧,将 pParent 的平衡因子减 1
- pCur 插入到 pParent 的右侧,将 pParent 的平衡因子加 1
此时,pParent 的平衡因子可能有三种情况:0、正负 1、正负 2。
- 0:说明插入之前是正负 1,插入后被调整为 0,满足 AVL 性质插入成功
- 正负 1:说明插入之前是 0,插入后被调整为正负 1,此时 pParent 变高,需要继续向上更新
- 正负 2:说明插入之前是正负 1,插入后被调整为正负 2,此时破坏了规定,需要旋转处理
/// @brief 插入指定节点
/// @param kv 待插入的节点
/// @return 插入成功返回 true,失败返回 false
bool Insert(const pair<K, V>& kv) {if (_root == nullptr) {_root = new Node(kv);return true;}// 先找到要插入的位置Node* parent = nullptr;Node* cur = _root;while (cur != nullptr) {if (kv.first > cur->_kv.first) {parent = cur;cur = cur->_right;} else if (kv.first < cur->_kv.first) {parent = cur;cur = cur->_left;} else {// 已经存在,插入失败return false;}}// 将节点插入cur = new Node(kv);if (kv.first > parent->_kv.first) {parent->_right = cur;cur->_parent = parent;} else {parent->_left = cur;cur->_parent = parent;}// 更新平衡因子,直到正常while (parent != nullptr) {// 调整父亲的平衡因子if (parent->_left == cur) {--parent->_bf;} else {++parent->_bf;}if (parent->_bf == 0) {// 此时不需要再继续调整了,直接退出break;} else if (parent->_bf == 1 || parent->_bf == -1) {// 此时需要继续向上调整cur = parent;parent = parent->_parent;} else if (parent->_bf == 2 || parent->_bf == -2) {// 此时需要旋转处理if (parent->_bf == -2 && cur->_bf == -1) {RotateR(parent);} else if (parent->_bf == 2 && cur->_bf == 1) {RotateL(parent);} else if (parent->_bf == -2 && cur->_bf == 1) {RotateLR(parent);} else if (parent->_bf == 2 && cur->_bf == -1) {RotateRL(parent);} else {assert(false);}// 旋转完了就平衡了,直接退出break;} else {// 此时说明之前就处理错了assert(false);} // end of if (parent->_bf == 0)} // end of while (parent != nullptr)return true;
}
旋转
假设平衡因子为正负 2 的节点为 X,由于节点最多拥有两个子节点,因此可以分为四种情况:
- 插入点位于 X 的左子节点的左子树——左左:右单旋
- 插入点位于 X 的左子节点的右子树——左右:左右双旋
- 插入点位于 X 的右子节点的右子树——右右:左单旋
- 插入点位于 X 的右子节点的左子树——右左:右左双旋

右单旋

假设平衡因子为正负 2 的节点为 parent,parent 的父节点为 pParent,parent 的左子树为 subL,subL 的右子树为 subLR。
右单旋的操作流程:
- 让 subLR 作为 parent 的左子树
- 让 parent 作为 subL 的右子树
- 让 subL 作为整个子树的新根
- 更新平衡因子
/// @brief 进行右单旋
/// @param parent 平衡因子为正负 2 的节点
void RotateR(Node* parent) {Node* pParent = parent->_parent;Node* subL = parent->_left;Node* subLR = parent->_left->_right;// 更改链接关系// 1. subLR 作为 parent 的左子树parent->_left = subLR;if (subLR != nullptr) {subLR->_parent = parent;}// 2. parent 作为 subL 的右子树subL->_right = parent;parent->_parent = subL;// 3. subL 作为整个子树的新根if (parent == _root) {// parent 为 _root,此时令 subL 为 _root_root = subL;subL->_parent = nullptr;} else {// parent 不为 _root,pParent 也就不为空if (parent == pParent->_left) {pParent->_left = subL;} else {pParent->_right = subL;}subL->_parent = pParent;}// 4. 更新平衡因子// 观察上图明显可知subL->_bf = 0;parent->_bf = 0;
}
左单旋
左单旋与右单旋类似,只是方向不同。
假设平衡因子为正负 2 的节点为 parent,parent 的父节点为 pParent,parent 的右子树为 subR,subR 的左子树为 subRL。
左单旋的操作流程:
- 让 subRL 作为 parent 的右子树
- 让 parent 作为 subR 的左子树
- 让 subR 作为整个子树的新根
- 更新平衡因子
/// @brief 进行左单旋
/// @param parent 平衡因子为正负 2 的节点
void RotateL(Node* parent) {Node* pParetn = parent->_parent;Node* subR = parent->_right;Node* subRL = parent->_right->_left;// 更改链接关系// 1. subRL 作为 parent 的右子树parent->_right = subRL;if (subRL != nullptr) {subRL->_parent = parent;}// 2. parent 作为 subR 的左子树subR->_left = parent;parent->_parent = subR;// 3. subR 作为整个子树的新根if (parent == _root) {_root = subR;subR->_parent = nullptr;} else {if (parent == pParetn->_left) {pParetn->_left = subR;} else {pParetn->_right = subR;}subR->_parent = pParetn;}// 4. 更新平衡因子subR->_bf = 0;parent->_bf = 0;
}
左右双旋

假设平衡因子为正负 2 的节点为 parent,parent 的左子树为 subL,subL 的右子树为 subLR。
左右双旋就是对 subL 进行一次左单旋,对 parent 进行一次右单旋。双旋也就完成了,要注意的是双旋后平衡因子的更新。
此时分三种情况:
- 新插入的节点是 subLR 的右子树

- 新插入的节点是 subLR 的左子树
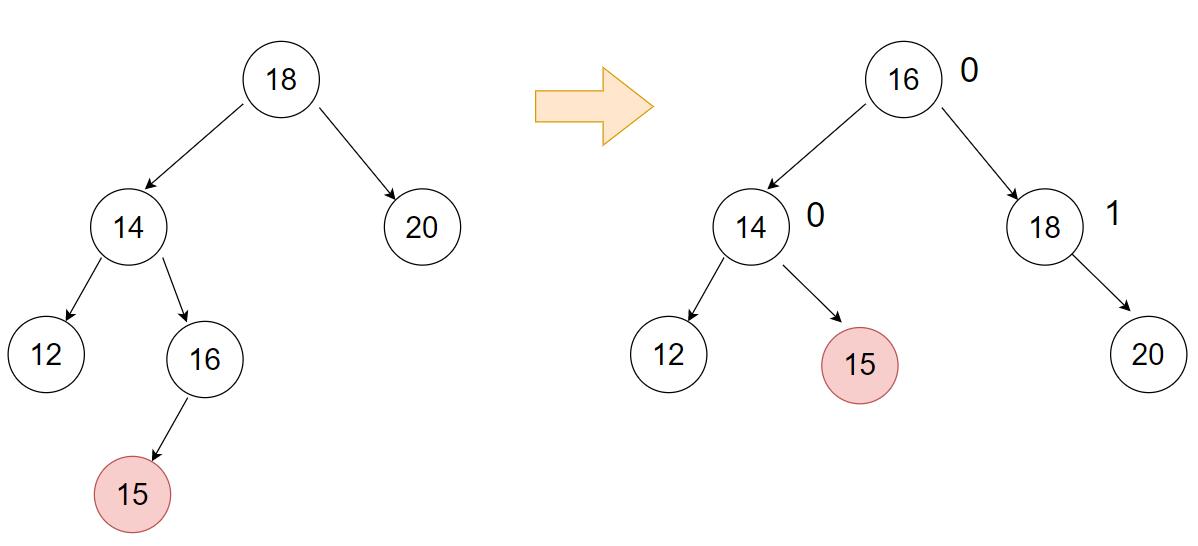
- 新插入的是 subLR
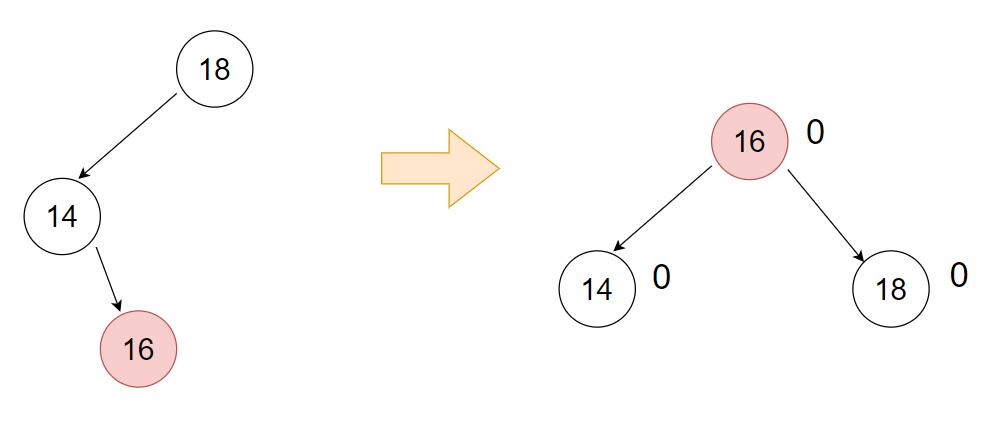
结合上述情况,写出如下代码:
/// @brief 进行左右双旋
/// @param parent 平衡因子为正负 2 的节点
void RotateLR(Node* parent) {Node* subL = parent->_left;Node* subLR = parent->_left->_right;int bf = subLR->_bf;RotateL(subL);RotateR(parent);if (bf == 1) {// 新插入节点是 subLR 的右子树parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;} else if (bf == -1) {// 新插入的节点是 subLR 的左子树parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;} else if (bf == 0) {// 新插入的节点是 subLRparent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;} else {assert(false);}
}
右左双旋
假设平衡因子为正负 2 的节点为 parent,parent 的右子树为 subR,subR 的左子树为 subRL。
右左双旋就是对 subR 进行一次右单旋,对 parent 进行一次左单旋。流程和左右双旋一样,这里就不过多介绍了。
void RotateRL(Node* parent) {Node* subR = parent->_right;Node* subRL = parent->_right->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if (bf == 1) {// 新插入节点是 subRL 的右子树parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;} else if (bf == -1) {// 新插入的节点是 subRL 的左子树parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;} else if (bf == 0) {// 新插入的节点是 subRLparent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;} else {assert(false);}
}
相关文章:

AVL 树实现
AVL 树的概念 也许因为插入的值不够随机,也许因为经过某些插入或删除操作,二叉搜索树可能会失去平衡,甚至可能退化为单链表,造成搜索效率低。 AVL Tree 是一个「加上了额外平衡条件」的二叉搜索树,其平衡条件的建立是…...

跟我学c++高级篇——模板元编程之八惰性加载
一、Lazy evaluation 惰性加载或者延迟计算,在前面的文章《跟我学c中级篇——迟延计算》中分析过。叫法怎么叫都可以,只要大家明白这个意思即可。Lazy evaluation一般可用于下面的情况: 1、模板中的对象非立刻的模板实例化,也就是…...

【Python入门第二十二天】Python 类和对象
Python 类/对象 Python 是一种面向对象的编程语言。 Python 中的几乎所有东西都是对象,拥有属性和方法。 类(Class)类似对象构造函数,或者是用于创建对象的“蓝图”。 创建类 如需创建类,请使用 class 关键字&…...

qml的进度条
QML是一种用于创建动态用户界面的声明式语言,它支持使用JavaScript表达式来定义属性绑定和信号处理器。在本文中,我们将介绍如何使用JavaScript在QML中绘制一个进度条(ProgressBar),并设置其前景色和背景色。进度条是一…...
Pycharm补丁包使用教程
虽然社区版在大多情况下已经够用,但是有很多功能都是没有的,对照起一些教程之类的就很不方便 现在直接教一种简单中的简单的补丁包使用方法 我这里用的是 pycharm 19.2.6 注意右下角的configure 一般别的方法都是 打开,然后添加路径&#…...

用VAE生成图像
用VAE生成图像自编码器AE,auto-encoderVAE讲讲为什么是log_var为什么要用重参数化技巧用VAE生成图像变分自编码器是自编码器的改进版本,自编码器AE是一种无监督学习,但它无法产生新的内容,变分自编码器对其潜在空间进行拓展&#…...
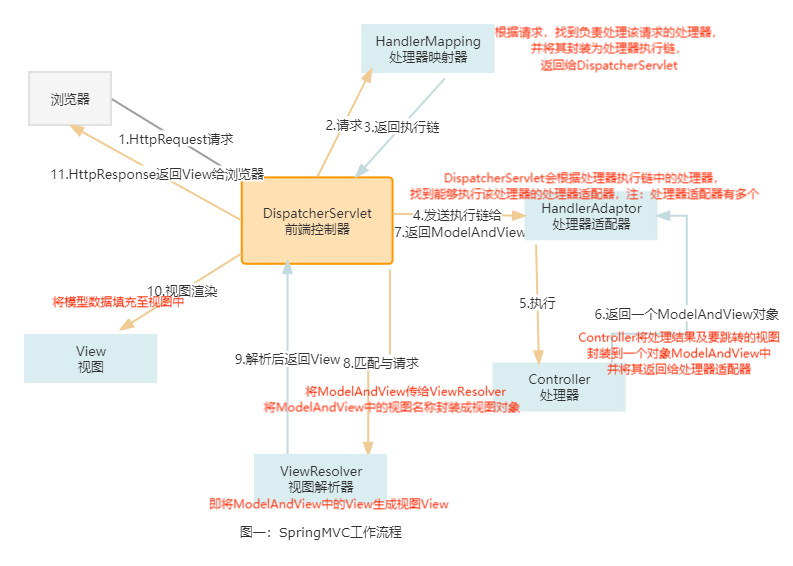
你只会说MVC模型是什么但是不会实现?今天带你走通Web、Servlet、MVC、SpringMVC。代码演示很清晰
文章目录HTTP请求和HTTP响应从0手写一个Web服务器,看看能有多累人使用Servlet实现一个服务器,看看多简单Serlvet的创建Servlet的运行Servlet的其他问题Servlet这么爽,我们简单地探索一下它的原理JSP跟Servlet合作啦,我们来看一下他…...
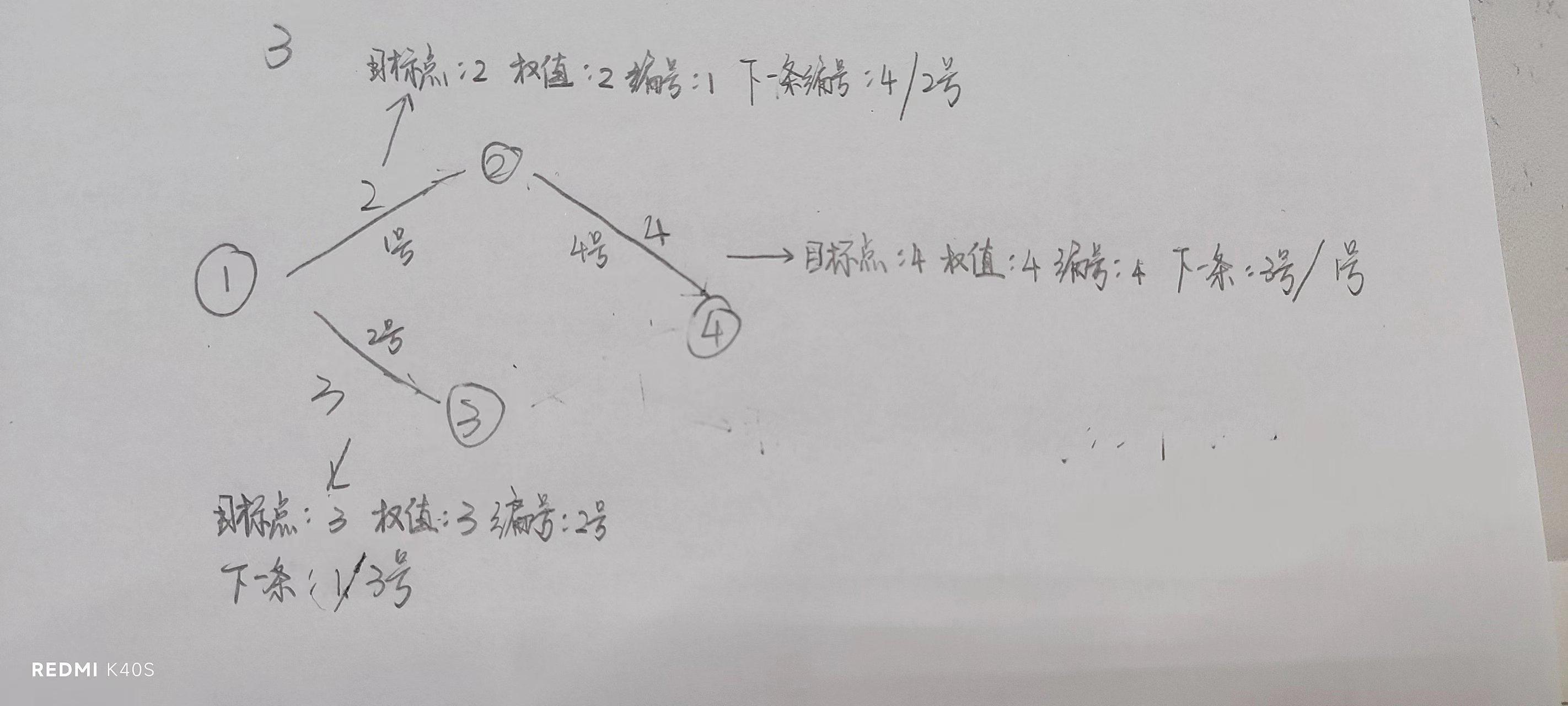
C++中邻接矩阵、邻接表、链式前向星具体用法及讲解
图论在提高组中几乎占据半壁江山,而今天要讲的就是如何存储一个图一.邻接矩阵原理要建立一个图,根本的要素就是边和点而想要让计算机存储边和点就需要用到一些数据结构邻接矩阵是最简单的他使用了一个二维数组,来表示一个图假设数组名为map那…...
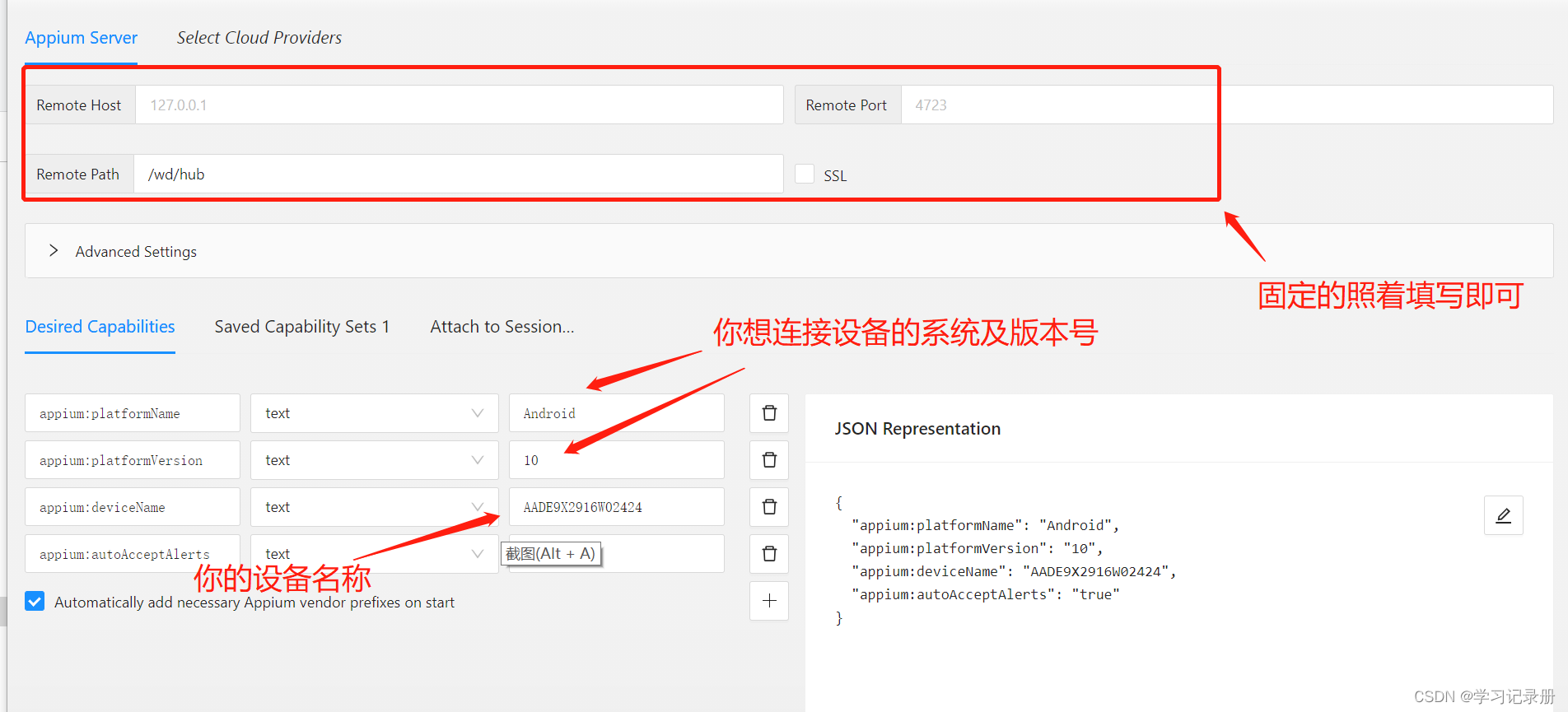
appium的安装详解
安装appium 爬虫手机APP需要实现自动化,所以要使用appnium来实现点击,输入,滑动等操作。由于appnium的安装较为繁琐,所以特意整理一篇文章来展示安装的详细过程过程中。 安装appnium共有3个步骤 安装 Android SDK安装 JDK安装 …...
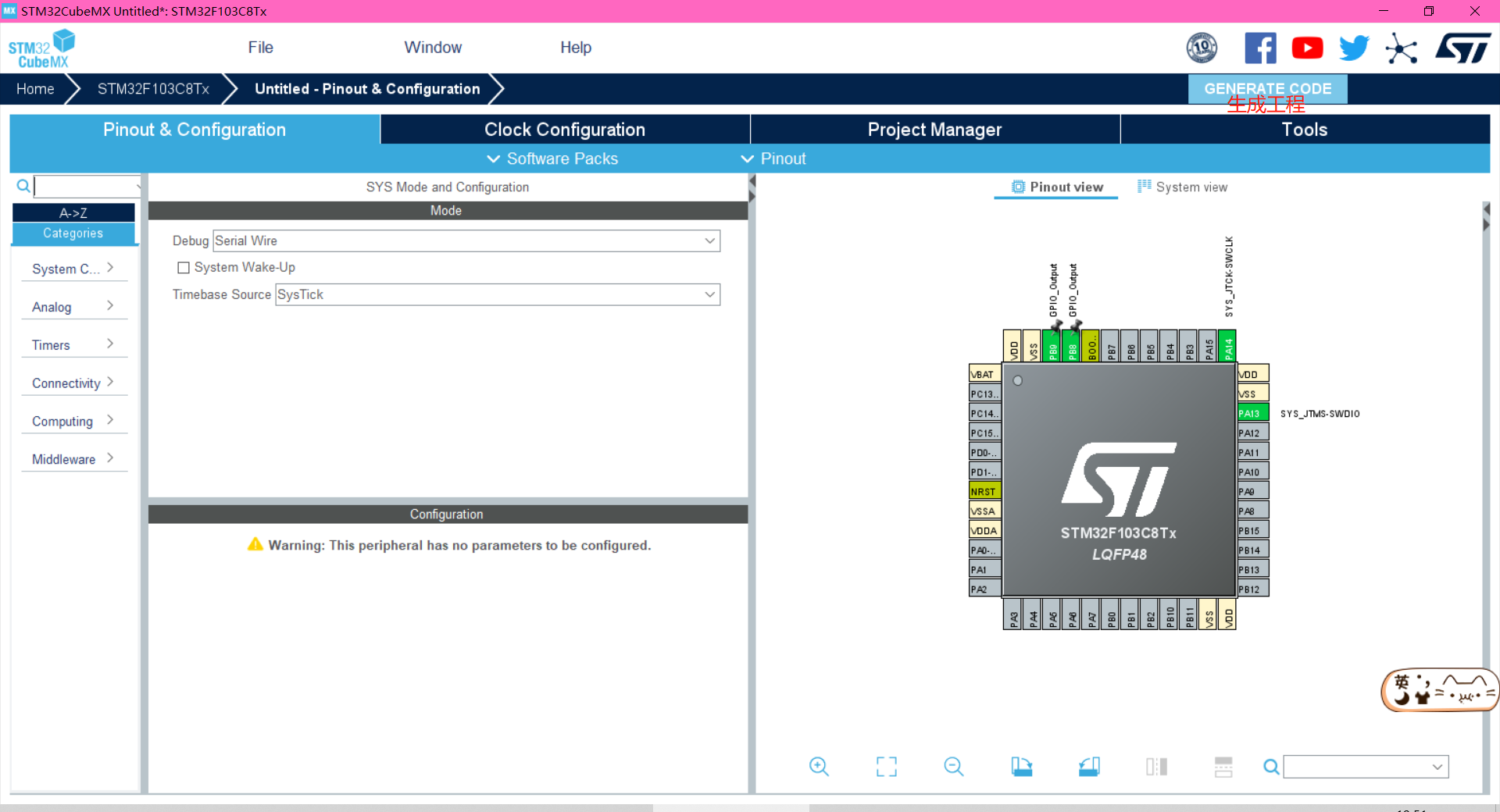
STM32之 串口
串口通信串行接口简称串口,也称串行通信接口或串行通讯接口(通常指COM接口),是采用串行通信方 式的扩展接口。串行接口(Serial Interface)是指数据一位一位地顺序传送。其特点是通信线路简 单,只…...

CSDN 编程竞赛三十三期题解
竞赛总览 CSDN 编程竞赛三十三期题解:比赛详情 (csdn.net) 竞赛题解 题目1、奇偶排序 给定一个存放整数的数组,重新排列数组使得数组左边为奇数,右边为偶数(奇数和偶数的顺序根据输入的数字顺序排列)。 第七期竞赛…...
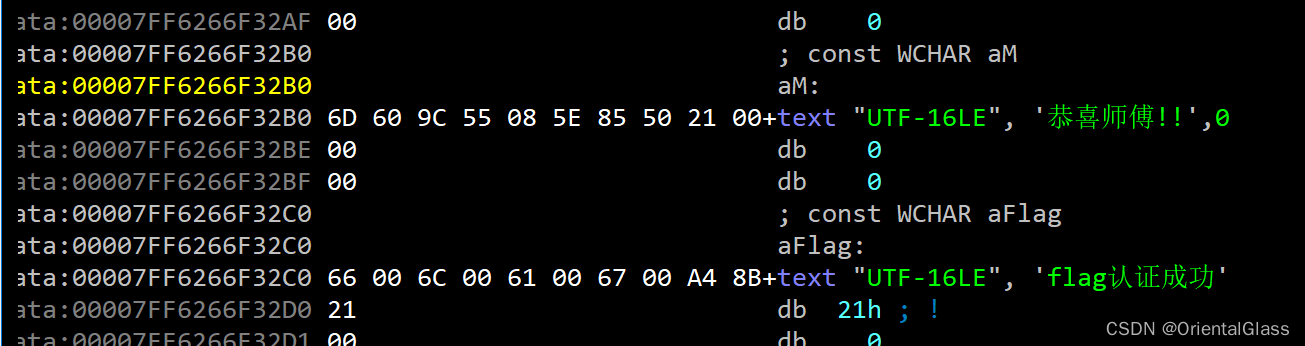
逆向练习之 mingyue.exe wp
目录 一.查壳 二.主函数 三.operate函数 四.storage函数及4618和4620指针功能的解释 五.judge函数 六.求解flag 七.其他--ida字符识别问题 一.查壳 64位无壳 二.主函数 1.这里的pointer_4618和4620是两个相邻的八字节内存单元,其中4620是字符串链表表头head 2.puts和s…...

LeetCode 热题 HOT 100 Java 题解 -- Part 3
练习地址 Part 1 : https://blog.csdn.net/qq_41080854/article/details/128829494 Part 2 : https://blog.csdn.net/qq_41080854/article/details/129278336 LeetCode 热题 HOT 100 Java 题解 -- Part 376. 最佳买卖股票时机含冷冻期77. 戳气球78. 零钱兑换79. 打家劫舍 III…...

QML键盘事件
在QML中,当有一个按键按下或释放时,会产生一个键盘事件,将其传递给获得有焦点的QML项目(讲focus属性设置为true,则获得焦点)。 按键处理的基本流程: Qt接收密钥操作并生成密钥事件。如果 QQuic…...

跨域问题怎么解决
解决跨域,原因:域名不同,域名相同端口不同;二级域名不同 什么是跨域? 就是两个项目之间通讯,如果访问的域名与ajax访问的地址不一致情况,默认情况浏览器有一个安全机制。 postman不一定能测试…...

微服务网关Gateway和Zuul的区别
spring-cloud-Gateway是spring-cloud的一个子项目。而zuul则是netflix公司的项目,只是spring将zuul集成在spring-cloud中使用而已。 因为zuul2.0连续跳票和zuul1的性能表现不是很理想,所以催生了spring团队开发了Gateway项目。 Zuul: 使用的…...
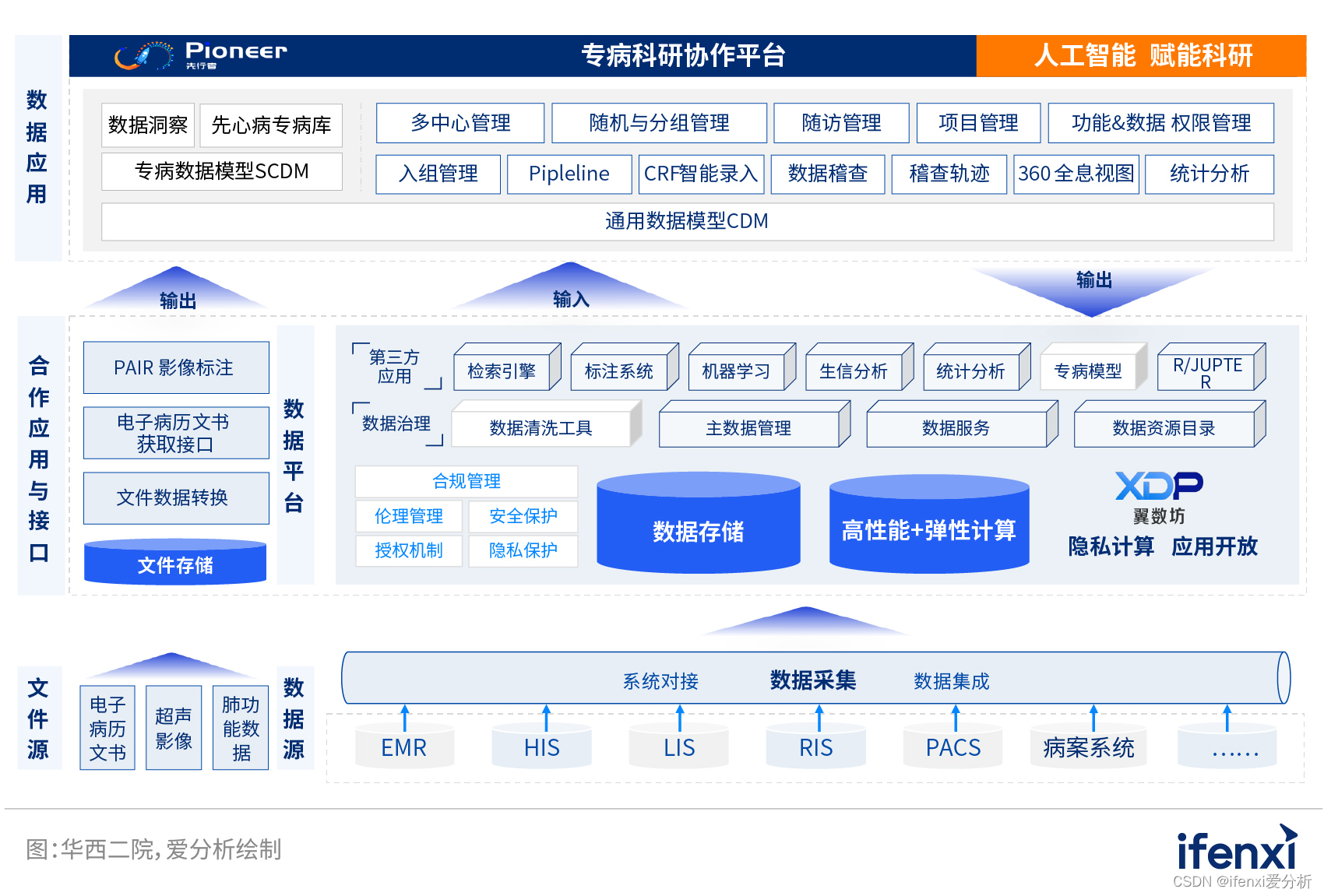
专访华西二院吴邦华:隐私计算+AI全栈技术,构筑智慧医院建设的坚实数据底座|爱分析访谈
从IT时代步入DT时代,医疗大数据成为智慧医院建设的重要驱动力。经过多年信息化系统建设,很多医院已经积累了大量的医疗数据资源,但由于各业务系统间数据孤岛化严重、系统架构落后、数据缺乏深度治理等问题存在,导致现有数据深度及…...
)
《C++ Primer Plus》第18章:探讨 C++ 新标准(6)
可变参数模板 可变参数模板(variadic template)让您能够创建这样的模板函数和模板类,即可接收可变数量的参数。这里介绍可变参数模板函数。例如,假设要编写一个函数,它可接受任意数量的参数,参数的类型只需…...

.Net Core中使用是SQL Server的邮件发送功能
.Net Core中使用是sqlserver的邮件发送功能准备需求启用SQL Server的电子邮件功能检查和测试在.net Core中调用在sqlsrver的管理中有一个数据库邮件功能,再此可以使用sqlserver来自动发送一些邮件,但是有一些需要插入附件的邮件则需要使用程序代码来解决,下面就是使用C#来调用s…...

Nginx优化服务和防盗链
Nginx优化服务和防盗链一、长连接1、修改主配置文件2、测试3、在主配置文件添加4、验证二、Nginx第三方模块1、开源的echo模块2、查看是否成功3、加echo模块步骤4、网页测试验证三、搭建虚拟主机1、编译安装好nginx后,对主配置文件进行修改2、创建文件3、验证四、防…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...
