Java二叉树的遍历以及最大深度问题
Java学习+面试指南:https://javaxiaobear.cn
1、树的相关概念
1、树的基本定义
树是我们计算机中非常重要的一种数据结构,同时使用树这种数据结构,可以描述现实生活中的很多事物,例如家谱、单位的组织架构、等等。
树是由n(n>=1)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
树具有以下特点:
- 每个结点有零个或多个子结点;
- 没有父结点的结点为根结点;
- 每一个非根结点只有一个父结点;
- 每个结点及其后代结点整体上可以看做是一棵树,称为当前结点的父结点的一个子树;
2、相关术语
1、结点的度
一个结点含有的子树的个数称为该结点的度;
2、叶子结点
度为0的结点称为叶结点,也可以叫做终端结点
3、分支结点
度不为0的结点称为分支结点,也可以叫做非终端结点
4、结点的层次
从根结点开始,根结点的层次为1,根的直接后继层次为2,以此类推
5、结点的层序编号
将树中的结点,按照从上层到下层,同层从左到右的次序排成一个线性序列,把他们编成连续的自然数。
6、树的度
树中所有结点的度的最大值
7、树的高度(深度)
树中结点的最大层次
8、森林
m(m>=0)个互不相交的树的集合,将一颗非空树的根结点删去,树就变成一个森林;给森林增加一个统一的根结点,森林就变成一棵树
9、孩子结点
一个结点的直接后继结点称为该结点的孩子结点
10、双亲结点(父结点)
一个结点的直接前驱称为该结点的双亲结点
11、兄弟结点
同一双亲结点的孩子结点间互称兄弟结点
2、二叉树
二叉树就是度不超过2的树(每个结点最多有两个子结点)
1、相关二叉树
1、满二叉树
一个二叉树,如果每一个层的结点树都达到最大值,则这个二叉树就是满二叉树。
2、完全二叉树
叶节点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树
2、创建二叉查找树
1、API设计
-
结点类
类名 Node<Key,Value> 构造方法 Node(Key key, Value value, Node left, Node right):创建Node对象 成员变量 1.public Node left:记录左子结点
2.public Node right:记录右子结点
3.public Key key:存储键
4.public Value value:存储值 -
二叉树
类名 BinaryTree<Key,value> 构造方法 BinaryTree():创建BinaryTree对象 成员变量 1.private Node root:记录根结点
2.private int N:记录树中元素的个数成员方法 1. public void put(Key key,Value value):向树中插入一个键值对
2.private Node put(Node x, Key key, Value val):给指定树x上,添加键一个键值对,并返回添加后的新树
3.public Value get(Key key):根据key,从树中找出对应的值
4.private Value get(Node x, Key key):从指定的树x中,找出key对应的值
5.public void delete(Key key):根据key,删除树中对应的键值对
6.private Node delete(Node x, Key key):删除指定树x上的键为key的键值对,并返回删除后的新树
7.public int size():获取树中元素的个数
1、put方法实现思路
如果当前树中没有任何一个结点,则直接把新结点当做根结点使用
如果当前树不为空,则从根结点开始:
如果新结点的key小于当前结点的key,则继续找当前结点的左子结点;
如果新结点的key大于当前结点的key,则继续找当前结点的右子结点;
如果新结点的key等于当前结点的key,则树中已经存在这样的结点,替换该结点的value值即可。
/*** 给指定树x上,添加键一个键值对,并返回添加后的新树* @param x 树节点* @param key 键* @param val 值* @return Node*/
public Node<Key, Value> put(Node<Key,Value> x, Key key, Value val){//当树为空时,该节点为根节点if(null == x){size++;return new Node<>(key, val, null, null);}int compare = key.compareTo(x.key);//如果compare > 0 ,则 key > x.key;继续x的右子节点if(0 < compare){x.right = put(x.right,key,val);}else if(0 > compare){//如果compare < 0 ,则 key < x.key;继续x的左子节点x.left = put(x.left,key,val);}else {//如果compare = 0 ,则 key = x.key;替换x.value的值x.value = val;}return x;
}
2、get方法实现思路
从根节点开始:
- 如果要查询的key小于当前结点的key,则继续找当前结点的左子结点;
- 如果要查询的key大于当前结点的key,则继续找当前结点的右子结点;
- 如果要查询的key等于当前结点的key,则树中返回当前结点的value。
/*** 从指定的树x中,找出key对应的值* @param x 节点* @param key 键* @return 节点*/
public Value getNode(Node<Key,Value> x, Key key){if (null == x){return null;}int compare = key.compareTo(x.key);if(0 < compare){return getNode(x.right,key);}else if(0 > compare){return getNode(x.left, key);}else {return x.value;}
}
3、delete方法的实现思路
- 找到被删除结点;
- 找到被删除结点右子树中的最小结点minNode
- 删除右子树中的最小结点
- 让被删除结点的左子树称为最小结点minNode的左子树,让被删除结点的右子树称为最小结点minNode的右子树
- 让被删除结点的父节点指向最小结点minNode
/*** 删除指定树x中的key对应的value,并返回删除后的新树* @param x* @param key* @return*/
public Node<Key,Value> delete(Node<Key, Value> x, Key key){if (null == x){return null;}int compare = key.compareTo(x.key);if(0 < compare){x.right = delete(x.right,key);}else if(0 > compare){x.left = delete(x.left,key);}else {//个数-1size--;//新结点的key等于当前结点的key,当前x就是要删除的结点if(x.right == null){return x.left;}if(x.left == null){return x.right;}//左右子结点都存在的情况下,找右子树最小的节点Node<Key, Value> minRight = x.right;while (null != minRight.left){minRight = minRight.left;}Node<Key, Value> node = x.right;while (node.left != null) {if (node.left.left == null) {node.left = null;} else {node = node.left;}}//让被删除结点的左子树称为最小结点minNode的左子树,让被删除结点的右子树称为最小结点minNode的右子树minRight.left = x.left;minRight.right = x.right;//让被删除结点的父节点指向最小结点minNodex = minRight;}return x;
}
4、完整代码
package com.xiaobear.BinaryTree;/*** @Author xiaobear* @date 2021年07月30日 13:50* @Description 二叉树*/
public class BinaryTree<Key extends Comparable<Key>,Value> {/*** 根节点*/private Node<Key,Value> root;/*** 节点数量*/private int size;public void put(Key key, Value val){root = put(root,key,val);}/*** 给指定树x上,添加键一个键值对,并返回添加后的新树* @param x 树节点* @param key 键* @param val 值* @return Node*/public Node<Key, Value> put(Node<Key,Value> x, Key key, Value val){//当树为空时,该节点为根节点if(null == x){size++;return new Node<>(key, val, null, null);}int compare = key.compareTo(x.key);//如果compare > 0 ,则 key > x.key;继续x的右子节点if(0 < compare){x.right = put(x.right,key,val);}else if(0 > compare){//如果compare < 0 ,则 key < x.key;继续x的左子节点x.left = put(x.left,key,val);}else {//如果compare = 0 ,则 key = x.key;替换x.value的值x.value = val;}return x;}/*** 根据key,从树中找出对应的值* @param key 键*/public Value getNode(Key key){return getNode(root,key);}/*** 从指定的树x中,找出key对应的值* @param x 节点* @param key 键* @return 节点*/public Value getNode(Node<Key,Value> x, Key key){if (null == x){return null;}int compare = key.compareTo(x.key);if(0 < compare){return getNode(x.right,key);}else if(0 > compare){return getNode(x.left, key);}else {return x.value;}}public void delete(Key key){root = delete(root, key);}/*** 删除指定树x中的key对应的value,并返回删除后的新树* @param x* @param key* @return*/public Node<Key,Value> delete(Node<Key, Value> x, Key key){if (null == x){return null;}int compare = key.compareTo(x.key);if(0 < compare){x.right = delete(x.right,key);}else if(0 > compare){x.left = delete(x.left,key);}else {//个数-1size--;//新结点的key等于当前结点的key,当前x就是要删除的结点if(x.right == null){return x.left;}if(x.left == null){return x.right;}//左右子结点都存在的情况下,找右子树最小的节点Node<Key, Value> minRight = x.right;while (null != minRight.left){minRight = minRight.left;}Node<Key, Value> node = x.right;while (node.left != null) {if (node.left.left == null) {node.left = null;} else {node = node.left;}}//让被删除结点的左子树称为最小结点minNode的左子树,让被删除结点的右子树称为最小结点minNode的右子树minRight.left = x.left;minRight.right = x.right;//让被删除结点的父节点指向最小结点minNodex = minRight;}return x;}public int size(){return size;}/*** 节点类* @param <Key>* @param <Value>*/private class Node<Key,Value>{public Key key;public Value value;public Node<Key,Value> left;public Node<Key, Value> right;public Node(Key key, Value value, Node left, Node<Key, Value> right) {this.key = key;this.value = value;this.left = left;this.right = right;}}
}
测试代码
public class BinaryTreeTest {public static void main(String[] args) {BinaryTree<Integer, String> binaryTree = new BinaryTree<>();binaryTree.put(1,"yhx");binaryTree.put(2,"love");binaryTree.put(3,"lwh");System.out.println(binaryTree.size());binaryTree.delete(2);String node = binaryTree.getNode(2);System.out.println(node);System.out.println(binaryTree.size());}
}
3、查找二叉树中最大/最小的键
1、最小的键
| 方法 | 描述 |
|---|---|
| public Key min() | 找出树中最小的键 |
| private Node min(Node x) | 找出指定树x中,最小键所在的结点 |
/*** 查找树中最小的键* @return*/
public Key minKey(){return minKey(root).key;
}/*** 根据二叉树的特点,左子树 < 右子树 so最小的键肯定是位于左边* @param x* @return*/
public Node<Key,Value> minKey(Node<Key,Value> x){if (x.left != null){return minKey(x.left);}else {return x;}
}
2、最大的键
| 方法 | 描述 |
|---|---|
| public Key max() | 找出树中最大的键 |
| public Node max(Node x) | 找出指定树x中,最大键所在的结点 |
/*** 查询树中最大的键* @return*/public Key maxKey(){return maxKey(root).key;}/*** 根据二叉树的特点,右子树 > 左子树 so最大的键肯定是位于右边* @param x* @return*/public Node<Key,Value> maxKey(Node<Key,Value> x){if(x.right != null){return maxKey(x.right);}else {return x;}}
3、二叉树的遍历
我们把树简单的画作上图中的样子,由一个根节点、一个左子树、一个右子树组成,那么按照根节点什么时候被访
问,我们可以把二叉树的遍历分为以下三种方式:
-
前序遍历
先访问根结点,然后再访问左子树,最后访问右子树
-
中序遍历
先访问左子树,中间访问根节点,最后访问右子树
-
后序遍历
先访问左子树,再访问右子树,最后访问根节点
1、前序遍历
前序遍历的API
| 方法 | 描述 |
|---|---|
| public Queue preErgodic() | 使用前序遍历,获取整个树中的所有键 |
| private void preErgodic(Node x,Queue keys) | 使用前序遍历,把指定树x中的所有键放入到keys队列中 |
/*** 前序遍历* @return*/
public Queue<Key> preErgodic(){Queue<Key> queue = new Queue<>();preErgodic(root,queue);return queue;
}/*** 前序遍历操作 先访问根结点,然后再访问左子树,最后访问右子树* @param x 根节点* @param queue 队列*/
private void preErgodic(Node<Key,Value> x, Queue<Key> queue){if (x == null) {return;}//把当前结点的key放入到队列中queue.enqueue(x.key);//访问左子树if(x.left != null){preErgodic(x.left,queue);}//访问右子树if(x.right != null){preErgodic(x.right,queue);}
}
2、中序遍历
中序遍历的API
| 方法 | 描述 |
|---|---|
| public Queue midErgodic() | 使用中序遍历,获取整个树中的所有键 |
| private void midErgodic(Node x,Queue keys) | 使用中序遍历,把指定树x中的所有键放入到keys队列中 |
/*** 中序遍历* @return*/public Queue<Key> midErgodic(){Queue<Key> queue = new Queue<>();midErgodic(root,queue);return queue;}/*** 先访问左子树,中间访问根节点,最后访问右子树* @param x* @param queue*/private void midErgodic(Node<Key,Value> x, Queue<Key> queue){if (x == null) {return;}//访问左子树if(x.left != null){preErgodic(x.left,queue);}//把当前结点的key放入到队列中queue.enqueue(x.key);//访问右子树if(x.right != null){preErgodic(x.right,queue);}}
3、后序遍历
后序遍历的API
| 方法 | 描述 |
|---|---|
| public Queue afterErgodic() | 使用后序遍历,获取整个树中的所有键 |
| private void afterErgodic(Node x,Queue keys) | 使用后序遍历,把指定树x中的所有键放入到keys队列中 |
/*** 后序遍历* @return*/public Queue<Key> afterErgodic(){Queue<Key> queue = new Queue<>();afterErgodic(root,queue);return queue;}/*** 先访问左子树,再访问右子树,最后访问根节点* @param x* @param queue*/private void afterErgodic(Node<Key,Value> x, Queue<Key> queue){if (x == null) {return;}//访问左子树if(x.left != null){preErgodic(x.left,queue);}//访问右子树if(x.right != null){preErgodic(x.right,queue);}//把当前结点的key放入到队列中queue.enqueue(x.key);}
4、测试
public class BinaryTreeErgodicTest {public static void main(String[] args) {BinaryTree<String, String> bt = new BinaryTree<>();bt.put("E", "5");bt.put("B", "2");bt.put("G", "7");bt.put("A", "1");bt.put("D", "4");bt.put("F", "6");bt.put("H", "8");bt.put("C", "3");//前序遍历Queue<String> preErgodic = bt.preErgodic();//中序遍历Queue<String> midErgodic = bt.midErgodic();//后序遍历Queue<String> afterErgodic = bt.afterErgodic();for (String key : preErgodic) {System.out.println(key+"=" +bt.getNode(key));}}
}
4、层次遍历
所谓的层序遍历,就是从根节点(第一层)开始,依次向下,获取每一层所有结点的值
层次遍历的结果是:EBGADFHC
| 方法 | 描述 |
|---|---|
| public Queue layerErgodic(): | 使用层序遍历,获取整个树中的所有键实 |
实现步骤:
- 创建队列,存储每一层的结点;
- 使用循环从队列中弹出一个结点:
- 获取当前结点的key
- 如果当前结点的左子结点不为空,则把左子结点放入到队列中
- 如果当前结点的右子结点不为空,则把右子结点放入到队列中
/*** 层次遍历* @return*/
public Queue<Key> layerErgodic(){//存储keyQueue<Key> keys = new Queue<>();//存储nodeQueue<Node<Key,Value>> nodes = new Queue<>();//入队头结点nodes.enqueue(root);while(!nodes.isEmpty()){//出队当前节点Node<Key,Value> dequeue = nodes.dequeue();//当前节点头入队keys.enqueue(dequeue.key);if(dequeue.left != null){nodes.enqueue(dequeue.left);}if(dequeue.right != null){nodes.enqueue(dequeue.right);}}return keys;
}
5、二叉树的最大深度
最大深度(树的根节点到最远叶子结点的最长路径上的结点数)
上面这颗树的最大深度为:E–>B–>D–>C,深度为4
| 方法 | 描述 |
|---|---|
| public int maxDepth() | 计算整棵树的最大深度 |
| private int maxDepth(Node x) | 计算指定树x的最大深度 |
实现步骤:
- 如果根结点为空,则最大深度为0;
- 计算左子树的最大深度;
- 计算右子树的最大深度;
- 当前树的最大深度=左子树的最大深度和右子树的最大深度中的较大者+1
/*** 计算整棵树的最大深度* @return*/public int maxDepth(){return maxDepth(root);}/*** 计算指定节点的最大深度* @param x* @return*/private int maxDepth(Node<Key,Value> x){if (x == null) {return 0;}int maxRight = 0;int maxLeft = 0;int maxDepth;if(x.left != null){maxLeft = maxDepth(x.left);}if (x.right != null) {maxRight = maxDepth(x.right);}maxDepth = maxLeft > maxRight ? maxLeft + 1 : maxRight + 1;return maxDepth;}
6、折纸问题
请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后展开。此时 折痕是凹下去的,即折痕突起的方向指向纸条的背面。如果从纸条的下边向上方连续对折2 次,压出折痕后展开,此时有三条折痕,从上到下依次是下折痕、下折痕和上折痕。
给定一 个输入参数N,代表纸条都从下边向上方连续对折N次,请从上到下打印所有折痕的方向 例如:N=1时,打印: down;N=2时,打印: down down up
分析
我们把对折后的纸张翻过来,让粉色朝下,这时把第一次对折产生的折痕看做是根结点,那第二次对折产生的下折痕就是该结点的左子结点,而第二次对折产生的上折痕就是该结点的右子结点,这样我们就可以使用树型数据结构来描述对折后产生的折痕。
这棵树有这样的特点:
- 根结点为下折痕;
- 每一个结点的左子结点为下折痕;
- 每一个结点的右子结点为上折痕;
实现步骤:
- 构建节点类
- 构建深度为n的折痕树
- 使用中序遍历,打印树中所有节点的内容
构建深度为N的折痕树:
- 第一次对折,只有一条折痕,创建根节点
- 如果不是第一次对折,则使用队列保存根节点
- 循环遍历队列
- 从队列中拿出一个节点
- 如果当前节点的左节点不为空,则把这个左节点加入队列中
- 如果当前节点的右节点不为空,则把这个右节点加入队列中
- 判断当前结点的左子结点和右子结点都为空,如果是,则需要为当前结点创建一个值为down的左子结点,一个值为up的右子结点。
public class PaperFolding {/*** 创建折痕树* @param size 深度*/public static Node createTree(int size){Node root = null;for (int i = 0; i < size; i++) {//第一次对折,只有一条折痕,创建根节点if (0 == i){root = new Node("down",null,null);}else {//如果不是第一次对折,则使用队列保存根节点Queue<Node> nodes = new Queue<>();nodes.enqueue(root);//循环遍历while(!nodes.isEmpty()){//从队列中拿出一个节点Node dequeue = nodes.dequeue();//如果当前节点的左节点不为空,则把这个左节点加入队列中if(dequeue.left != null){nodes.enqueue(dequeue.left);}//如果当前节点的右节点不为空,则把这个右节点加入队列中if(dequeue.right != null){nodes.enqueue(dequeue.right);}//判断当前结点的左子结点和右子结点都为空,则需要为当前结点创建一个值为down的左子结点,一个值为up的右子结点。if(dequeue.left == null && dequeue.right == null){dequeue.left = new Node("down",null,null);dequeue.right = new Node("up",null,null);}}}}return root;}/*** 采用中序遍历* @param root*/public static void printTree(Node root){if (root == null) {return;}printTree(root.left);System.out.print(root.item+" ");printTree(root.right);}/*** 节点类*/private static class Node{String item;Node left;Node right;public Node(String item, Node left, Node right) {this.item = item;this.left = left;this.right = right;}}public static void main(String[] args) {Node tree = createTree(2);printTree(tree);}
}
down down up

相关文章:

Java二叉树的遍历以及最大深度问题
Java学习面试指南:https://javaxiaobear.cn 1、树的相关概念 1、树的基本定义 树是我们计算机中非常重要的一种数据结构,同时使用树这种数据结构,可以描述现实生活中的很多事物,例如家谱、单位的组织架构、等等。 树是由n&#…...
Apollo 9.0搭建问题记录
虚拟机安装 可以看这个:https://blog.csdn.net/qq_45138078/article/details/129815408 写的很详细 内存 为了学习 Apollo ,所以只是使用了虚拟机,内存得大一点(128G),第一次,就是因为分配内…...

【心得】PHP文件包含高级利用攻击面个人笔记
目录 一、nginx日志文件包含 二、临时文件包含 三、php的session文件包含 四、pear文件包含 五 、远程文件包含 文件包含 include "/var/www/html/flag.php"; 一 文件名可控 $file$_GET[file]; include $file.".php"; //用php伪协议 ࿰…...

[scala] 列表常见用法
文章目录 不可变列表 List可变列表 ListBuffer 不可变列表 List 在 Scala 中,列表是一种不可变的数据结构,用于存储一系列元素。列表使用 List 类来表示,它提供了许多方法来操作和处理列表。 下面是一些常见的使用列表的示例: 创…...

python 使用urllib3发起post请求,携带json参数
当通过python脚本,发起http post请求,网络上大多是通过fields传递数据,然而这样,服务器收到的请求,但无法解析json数据。类似这些链接: Python urllib3库使用指南 软件测试|Python urllib3库使用指南 p…...
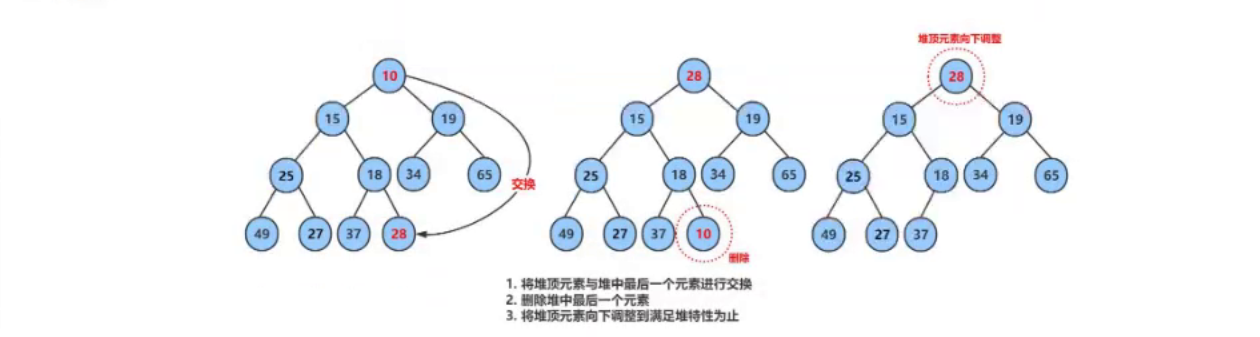
深入理解堆(Heap):一个强大的数据结构
. 个人主页:晓风飞 专栏:数据结构|Linux|C语言 路漫漫其修远兮,吾将上下而求索 文章目录 前言堆的实现基本操作结构体定义初始化堆(HeapInit)销毁堆(HeapDestroy) 重要函数交换函数(…...
抖音在线查权重系统源码,附带查询接口
抖音权重在线查询只需输入抖音主页链接,即可查询作品情况。 搭建教程 上传源码并解压 修改数据库“bygoukai.sql” 修改“config.php” 如需修改水印请修改第40行 如需修改限制次数,请修改第156行 访问域名user.php即可查看访问用户,停…...

Spring Framework和SpringBoot的区别
目录 一、前言 二、什么是Spring 三、什么是Spring Framework 四、什么是SpringBoot 五、使用Spring Framework构建工程 六、使用SpringBoot构建工程 七、总结 一、前言 作为Java程序员,我们都听说过Spring,也都使用过Spring的相关产品࿰…...
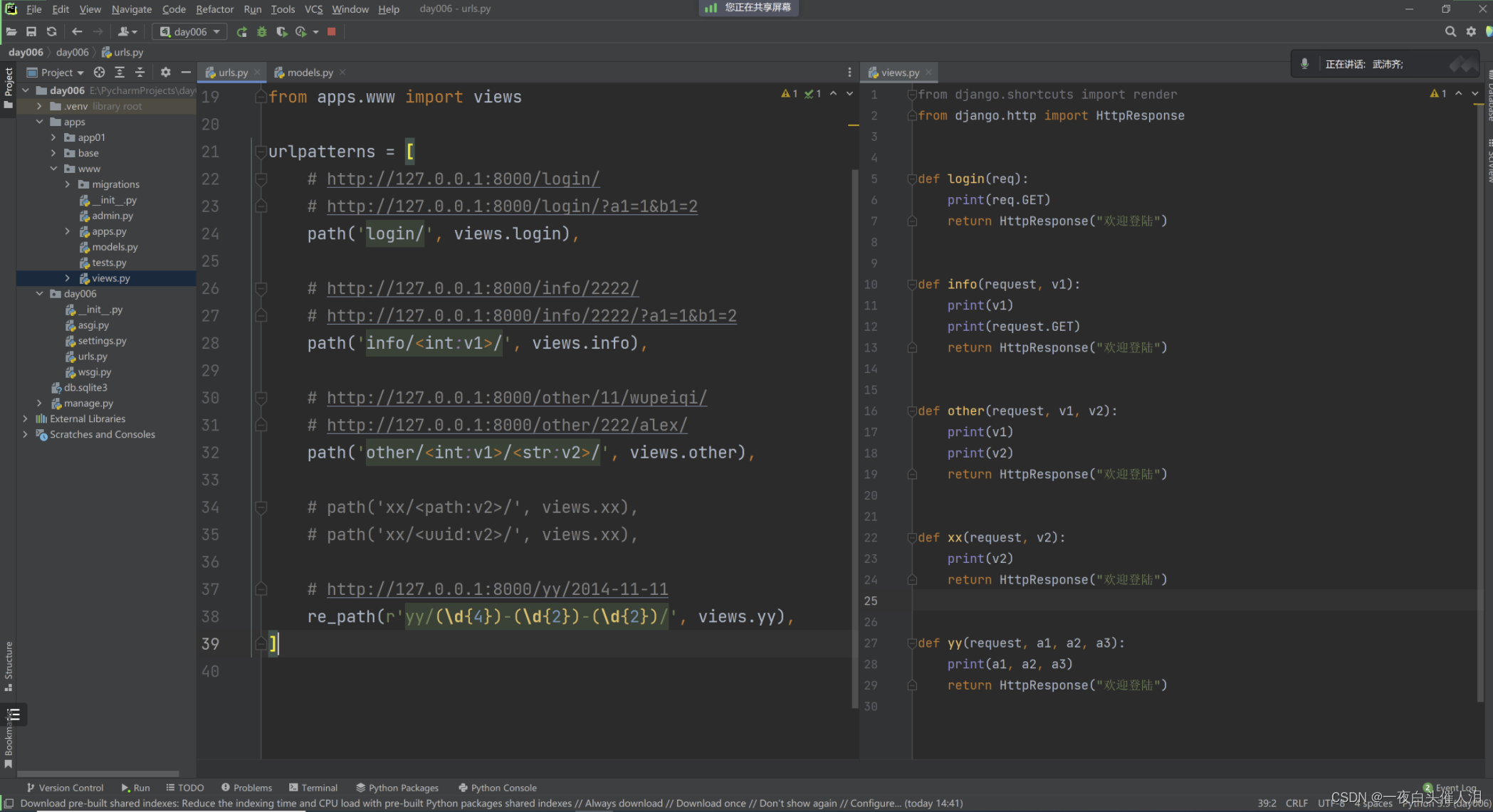
2024--Django平台开发-Django知识点(三)
day03 django知识点 项目相关路由相关 urls.py视图相关 views.py模版相关 templates资源相关 static/media 1.项目相关 新项目 开发时,可能遇到使用其他的版本。虚拟环境 老项目 打开项目虚拟环境 1.1 关于新项目 1.系统解释器命令行【学习】 C:/python38- p…...

Github 2024-01-08开源项目周报 Top14
根据Github Trendings的统计,本周(2024-01-08统计)共有14个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量Python项目5TypeScript项目3C项目2Dart项目1QML项目1Go项目1Shell项目1Rust项目1JavaScript项目1C#项目1 免费…...

vue3 的内置组件汇总
官方给出的说明: Fragment: Vue 3 组件不再要求有一个唯一的根节点,清除了很多无用的占位 div。Teleport: 允许组件渲染在别的元素内,主要开发弹窗组件的时候特别有用。Suspense: 异步组件,更方便开发有异步请求的组件。 一、fr…...
ARM工控机Node-red使用教程
嵌入式ARM工控机Node-red安装教程 从前车马很慢书信很远,而现在人们不停探索“科技改变生活”。 智能终端的出现改变了我们的生活方式,钡铼技术嵌入式工控机协助您灵活布建能源管理、大楼自动化、工业自动化、电动车充电站等各种多元性IoT应用ÿ…...
Visual Studio 发布程序自动更新 ClickOnce和AutoUpdater测试
文章目录 前言运行环境ClickOnce(Visual Studio 程序发布)IIS新建文件夹C# 控制台测试安装测试更新测试卸载 AutoUpdaterDotNET实现原理简单使用新建一个WPF项目 代码封装自动更新代码封装简单使用 总结 前言 虽然写的大部分都是不联网项目,…...
Codeforces Round 761 (Div. 2) E. Christmas Chocolates(思维题 树的直径 二进制性质 lca)
题目 n(n<2e5)个值,第i个值ai(0<ai<1e9),所有ai两两不同 初始时,选择两个位置x,y(x≠y),代表需要对这两个位置进行操作,要把其中一个值变成另一个 你可以执行若干次操作,每一次,你可…...
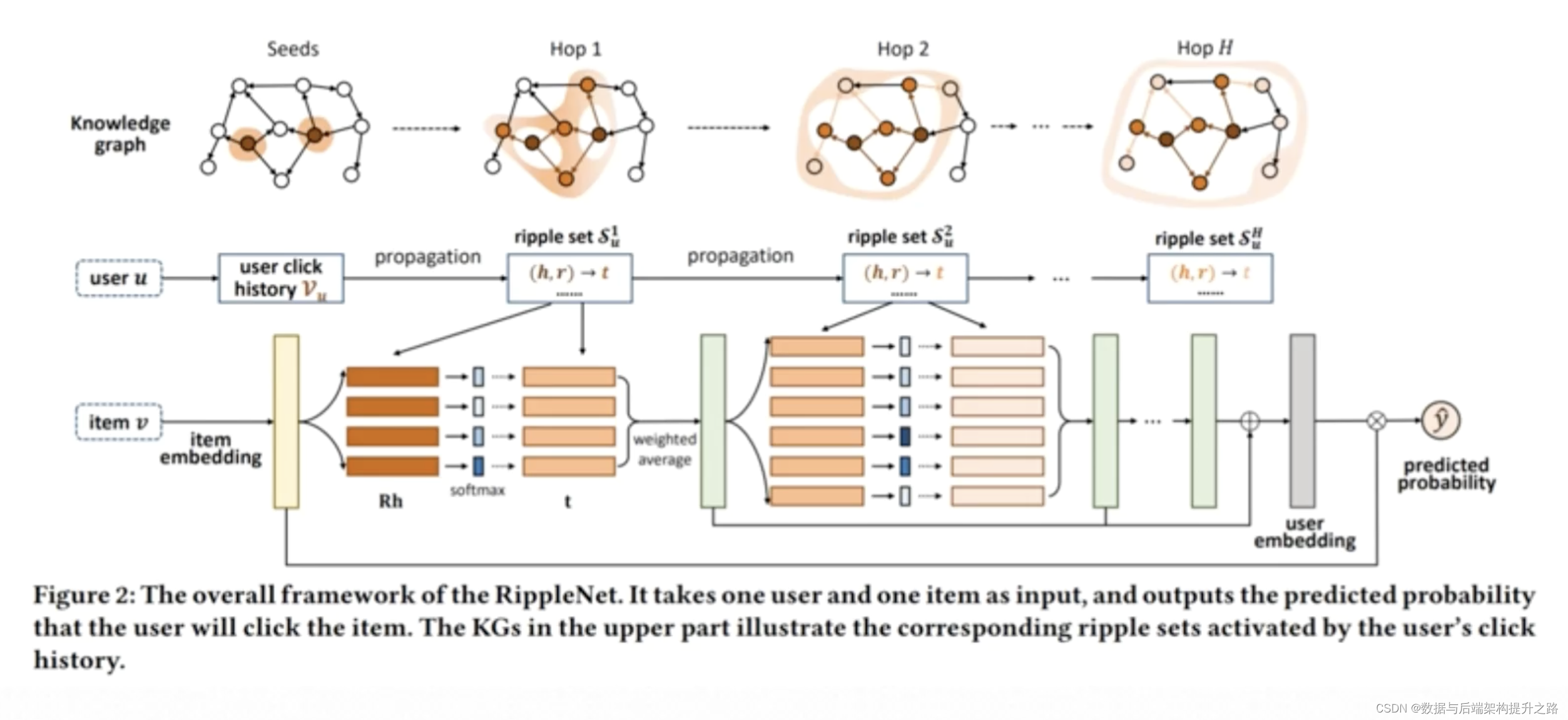
知识图谱之汽车实战案例综述与前瞻分析
知识图谱的前置介绍 什么是知识图谱 知识图谱本质(Knowledge Graph)上是一种叫做语义网络(semantic network ) 的知识库,即具有有向图结构的一个知识库;图的结点代表实体(entity)或者概念(con…...

网关Gateway
什么是网关? 网关实质上是一个网络通向其他网络的 IP 地址,是当前微服务项目的"统一入口"。 网关能做什么? 反向代理 、鉴权、 流量控制、 熔断、 日志监控等 图片原文:http://t.csdnimg.cn/SvUJh 核心概念 Router(…...
java 生成一个当前时间的时间搓
开发过程中 用时间搓数值格式存储 会更加精准 那么 我们在一些日常增删查改中就可以用时间搓来记录操作时间 就一行代码 long timestamp System.currentTimeMillis();他就能生成当前时间的时间搓 运行结果如下 然后 我们可以在 http://shijianchuo.wiicha.com/ 上进行转换查…...

金融中IC和IR的定义
当谈到金融领域时,IC(Information Coefficient)和IR(Information Ratio)通常是用来评估投资组合管理绩效的指标。它们都涉及到投资者对信息的利用和管理的效果。 信息系数(IC - Information Coefficient&a…...
Git(2):Git环境的安装
本教程里的git命令例子都是在Git Bash中演示的,会用到一些基本的linux命令,在此为大家提前列举: ls/ll 查看当前目录cat 查看文件内容touch 创建文件vi vi编辑器(使用vi编辑器是为了方便展示效果,学员可以记事本、edi…...

Pytest单元测试系列[v1.0.0][pytest插件常用技巧]
使用pytest-xdist并发执行测试 pytest-xdist:Run Tests in Parallel [https://pypi.python.org/pypi/pytest-xdist] 在自动化测试中有些资源只能同时被一个测试用例访问,如果不需要同时使用同一个资源,那么测试用例便可以并行执行 执行命令…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...
