强化学习的数学原理学习笔记 - 蒙特卡洛方法(Monte Carlo)
文章目录
- 概览:RL方法分类
- 蒙特卡洛方法(Monte Carlo,MC)
- MC Basic
- MC Exploring Starts
- 🟦MC ε-Greedy
本系列文章介绍强化学习基础知识与经典算法原理,大部分内容来自西湖大学赵世钰老师的强化学习的数学原理课程(参考资料1),并参考了部分参考资料2、3的内容进行补充。
系列博文索引:
- 强化学习的数学原理学习笔记 - RL基础知识
- 强化学习的数学原理学习笔记 - 基于模型(Model-based)
- 强化学习的数学原理学习笔记 - 蒙特卡洛方法(Monte Carlo)
- 强化学习的数学原理学习笔记 - 时序差分学习(Temporal Difference)
- 强化学习的数学原理学习笔记 - 值函数近似(Value Function Approximation)
- 强化学习的数学原理学习笔记 - 策略梯度(Policy Gradient)
- 强化学习的数学原理学习笔记 - Actor-Critic
参考资料:
- 【强化学习的数学原理】课程:从零开始到透彻理解(完结)(主要)
- Sutton & Barto Book: Reinforcement Learning: An Introduction
- 机器学习笔记
*注:【】内文字为个人想法,不一定准确
概览:RL方法分类
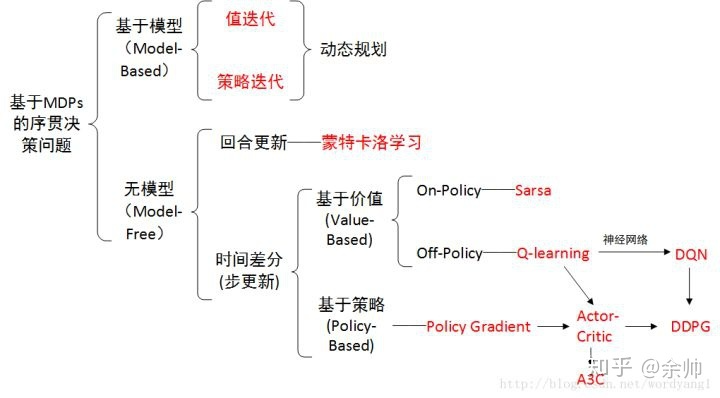
*图源:https://zhuanlan.zhihu.com/p/36494307
蒙特卡洛方法(Monte Carlo,MC)
求解RL问题,要么需要模型,要么需要数据。之前介绍了基于模型(model-based)的方法。然而在实际场景中,环境的模型(如状态转移函数)往往是未知的,这就需要用无模型(model-free)方法解决问题。
无模型的方法可以分为两大类:蒙特卡洛方法(Monte Carlo,MC)和时序差分学习(Temporal Difference,TD)。本文介绍蒙特卡洛方法。
蒙特卡洛思想:通过大数据量的样本采样来进行估计【本质上是大数定律的应用(基于独立同分布采样)】,将策略迭代中依赖于model的部分替换为model-free。
MC的核心idea:并非直接求解 q π ( s , a ) q_{\pi} (s, a) qπ(s,a)的准确值,而是基于数据(sample / experience)来估计 q π ( s , a ) q_{\pi} (s, a) qπ(s,a)的值。MC直接通过动作值的定义进行均值估计,即:
q π ( s , a ) = E π [ G t ∣ S t = s , A t = a ] ≈ 1 N ∑ i = 1 N g ( i ) ( s , a ) q_{\pi}(s, a) = \mathbb{E}_\pi [ G_t | S_t = s, A_t = a ] \approx \frac{1}{N} \sum^N_{i=1} g^{(i)} (s, a) qπ(s,a)=Eπ[Gt∣St=s,At=a]≈N1i=1∑Ng(i)(s,a)
其中 g ( i ) ( s , a ) g^{(i)} (s, a) g(i)(s,a)表示对于 G t G_t Gt的第 i i i个采样。
MC Basic
算法步骤:在第 k k k次迭代中,给定策略 π k \pi_k πk(随机初始策略: π 0 \pi_0 π0)
- 策略评估:对每个状态-动作对 ( s , a ) (s, a) (s,a),运行无穷(或足够多)次episode,估算 q π k ( s , a ) q_{\pi_{k}} (s, a) qπk(s,a)
- 策略提升:基于估算的 q π k ( s , a ) q_{\pi_{k}} (s, a) qπk(s,a),求解迭代策略 π k + 1 ( s ) = arg max π ∑ a π ( a ∣ s ) q π k ( s , a ) \pi_{k+1}(s) = \argmax_\pi \sum_a \pi(a|s) q_{\pi_{k}}(s, a) πk+1(s)=argmaxπ∑aπ(a∣s)qπk(s,a)
MC Basic与策略迭代的区别:在第 k k k次迭代中
- 策略迭代使用迭代方法求出状态值 v π k v_{\pi_k} vπk,并基于状态值求出动作值 q π k ( s , a ) q_{\pi_k} (s, a) qπk(s,a)
- MC Basic直接基于采样/经验均值估计 q π k ( s , a ) q_{\pi_k} (s, a) qπk(s,a)(不需要估计状态值)
*MC Basic只是用来说明MC的核心idea,并不会在实际中应用,因为其非常低效。
MC Exploring Starts
思想:提升MC Basic的效率
- 利用数据:对于一个轨迹,从后往前利用 ( s , a ) (s, a) (s,a)状态-动作对采样做估计
- 例如:对于轨迹 s 1 → a 2 s 2 → a 4 s 1 → a 2 s 2 → a 3 s 5 → a 1 ⋯ s_1 \xrightarrow{a_2} s_2 \xrightarrow{a_4} s_1 \xrightarrow{a_2} s_2 \xrightarrow{a_3} s_5 \xrightarrow{a_1} \cdots s1a2s2a4s1a2s2a3s5a1⋯,从后往前采样,即先估计 q π ( s 5 , a 1 ) q_\pi(s_5, a_1) qπ(s5,a1),再估计 q π ( s 2 , a 3 ) = R t + 4 + γ q π ( s 5 , a 1 ) q_\pi(s_2, a_3) = R_{t+4} + \gamma q_\pi(s_5, a_1) qπ(s2,a3)=Rt+4+γqπ(s5,a1),进而估计 q π ( s 1 , a 2 ) = R t + 3 + γ q π ( s 2 , a 3 ) q_\pi(s_1, a_2) = R_{t+3} + \gamma q_\pi(s_2, a_3) qπ(s1,a2)=Rt+3+γqπ(s2,a3),以此类推
- 更新策略:不必等待所有episode的数据收集完毕,直接基于单个episode进行估计,类似于截断策略迭代(单次估计不准确,但快)
- 这是通用策略迭代(Generalized Policy Iteration,GPI)的思想
MC Exploring Starts
- Exploring:探索每个 ( s , a ) (s, a) (s,a)状态-动作对
- Starts:从每个状态-动作对开始一个episode
- 与Visit对应:从其他的状态-动作对开始一个episode,但其轨迹能经过当前的状态-动作对
🟦MC ε-Greedy
Exploring Starts在实际中难以实现,考虑引入soft policy:随机(stochastic)选择动作
ε-Greedy策略:
π ( a ∣ s ) = { 1 − ε ∣ A ( s ) ∣ ( ∣ A ( s ) ∣ − 1 ) , for the greedy action, ε ∣ A ( s ) ∣ , for other ∣ A ( s ) ∣ − 1 actions. \pi(a|s) = \begin{cases} 1-\frac{\varepsilon}{|\mathcal{A}(s)|} (|\mathcal{A}(s)|-1), &\text{for the greedy action, } \\ \frac{\varepsilon}{|\mathcal{A}(s)|}, &\text{for other } |\mathcal{A}(s)|-1 \text{ actions.} \end{cases} π(a∣s)={1−∣A(s)∣ε(∣A(s)∣−1),∣A(s)∣ε,for the greedy action, for other ∣A(s)∣−1 actions.
其中, ε ∈ [ 0 , 1 ] \varepsilon \in [0,1] ε∈[0,1], ∣ A ( s ) ∣ |\mathcal{A}(s)| ∣A(s)∣表示状态 s s s下的动作数量。
- 直观理解:以较高概率选择贪心动作(greedy action),以较低均等概率选择其他动作
- 特性:选择贪心动作的概率永远不低于选择其他动作的概率
- 目的:平衡exploitation(探索)和exploration(利用)
- ε = 0 \varepsilon = 0 ε=0:侧重于利用,永远选择贪心动作
- ε = 1 \varepsilon = 1 ε=1:侧重于探索,以均等概率选择所有动作(均匀分布)
MC ε-Greedy:在策略提升阶段,求解下式
π k + 1 ( s ) = arg max π ∈ Π ε ∑ a π ( a ∣ s ) q π k ( s , a ) \pi_{k+1}(s) = \argmax_{\color{red}\pi \in \Pi_\varepsilon} \sum_a \pi(a|s) q_{\pi_{k}}(s, a) πk+1(s)=π∈Πεargmaxa∑π(a∣s)qπk(s,a)
其中, π ∈ Π ε \pi \in \Pi_\varepsilon π∈Πε表示所有ε-Greedy策略的集合。得到的最优策略为:
π k + 1 ( a ∣ s ) = { 1 − ε ∣ A ( s ) ∣ ( ∣ A ( s ) ∣ − 1 ) , a = a k ∗ , ε ∣ A ( s ) ∣ , a ≠ a k ∗ . \pi_{k+1}(a|s) = \begin{cases} 1-\frac{\varepsilon}{|\mathcal{A}(s)|} (|\mathcal{A}(s)|-1), &a = a_k^*, \\ \frac{\varepsilon}{|\mathcal{A}(s)|}, &a \neq a_k^*. \end{cases} πk+1(a∣s)={1−∣A(s)∣ε(∣A(s)∣−1),∣A(s)∣ε,a=ak∗,a=ak∗.
MC ε-Greedy与MC Basic和MC Exploring Starts的区别:
- 后二者求解的范围是 π ∈ Π \pi \in \Pi π∈Π,即所有策略的集合
- 后二者得到的是确定性策略,前者得到的是随机策略
MC ε-Greedy与MC Exploring Starts的唯一区别在于ε-Greedy策略,因此MC ε-Greedy不需要Exploring Starts。
MC ε-Greedy通过探索性牺牲了最优性,但可以通过设置一个较小的ε(如0.1)进行平衡
- 在实际中,可以为ε设置一个较大的初始值,随着迭代轮数逐渐减小其取值
- ε的值越大,最终策略的最优性越差
最终训练得到的策略,可以去掉ε,直接使用greedy的确定性策略(consistent)。
相关文章:

强化学习的数学原理学习笔记 - 蒙特卡洛方法(Monte Carlo)
文章目录 概览:RL方法分类蒙特卡洛方法(Monte Carlo,MC)MC BasicMC Exploring Starts🟦MC ε-Greedy 本系列文章介绍强化学习基础知识与经典算法原理,大部分内容来自西湖大学赵世钰老师的强化学习的数学原理…...
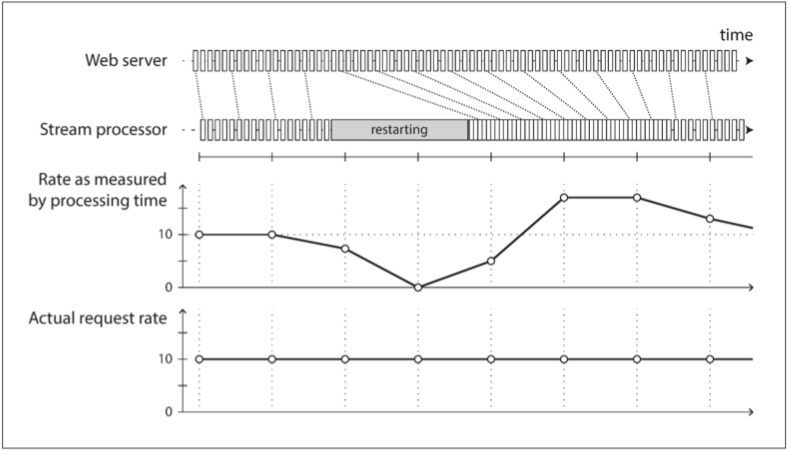
DDIA 第十一章:流处理
本文是《数据密集型应用系统设计》(DDIA)的读书笔记,一共十二章,我已经全部阅读并且整理完毕。 采用一问一答的形式,并且用列表形式整理了原文。 笔记的内容大概是原文的 1/5 ~ 1/3,所以你如果没有很多时间…...

webpack知识点总结(高级应用篇)
除开公共基础配置之外,我们意识到两点: 1. 开发环境(modedevelopment),追求强大的开发功能和效率,配置各种方便开 发的功能;2. 生产环境(modeproduction),追求更小更轻量的bundle(即打包产物); 而所谓高级应用,实际上就是进行 Webpack 优化…...

均匀与准均匀 B样条算法
B 样条曲线的定义 p ( t ) ∑ i 0 n P i F i , k ( t ) p(t) \sum_{i0}{n} P_i F_{i, k}(t) p(t)i0∑nPiFi,k(t) 方程中 n 1 n1 n1 个控制点, P i P_i Pi, i 0 , 1 , ⋯ n i0, 1, \cdots n i0,1,⋯n 要用到 n 1 n1 n1 个 k k k 次 B 样条基函数 …...
答案解析)
2023年12 月电子学会Python等级考试试卷(一级)答案解析
青少年软件编程(Python)等级考试试卷(一级) 分数:100 题数:37 一、单选题(共25题,共50分) 1. 下列程序运行的结果是?( ) print(hello) print(world) A. helloworld...
启发式算法解决TSP、0/1背包和电路板问题
1. Las Vegas 题目 设计一个 Las Vegas 随机算法,求解电路板布线问题。将该算法与分支限界算法结合,观察求解效率。 代码 python代码如下: # -*- coding: utf-8 -*- """ Date : 2024/1/4 Time : 16:21 Author : …...

阿里云新用户的定义与权益
随着云计算的普及,阿里云作为国内领先的云计算服务提供商,吸引了越来越多的用户。对于新用户来说,了解阿里云新用户的定义和相关权益非常重要,因为它关系到用户能否享受到更多的优惠和服务。 一、阿里云新用户的定义 阿里云新用户…...

go语言多线程操作
目录 引言 一、如何实现多线程 1. 线程的创建与管理: 2. 共享资源与同步: 3. 线程间通信: 4. 线程的生命周期管理: 5. 线程安全: 6. 考虑并发问题: 7. 性能与资源利用: 8. 特定语言或框架的工具和库: 二、go语言多线程 Goroutine 1. 轻量级: 2. 动态栈: 3. 调度:…...

GreatSQL社区2023全年技术文章总结
GreatSQL社区自成立以来一直致力于为广大的数据库爱好者提供一个交流与学习的平台。在2023年,我们见证了社区的蓬勃发展,见证了众多技术文章的诞生与分享。 此篇总结呈现GreatSQL社区2023年社区技术文章在CSDN发布的全部。这些文章涵盖了GreatSQL、MGR、…...

【论文阅读笔记】Stable View Synthesis 和 Enhanced Stable View Synthesis
目录 Stable View Synthesis摘要引言 Enhanced Stable View Synthesis 从Mip-NeRF360的对比实验中找到的两篇文献,使用了卷积神经网络进行渲染和新视角合成,特此记录一下 ToDo Stable View Synthesis paper:https://readpaper.com/pdf-ann…...
网络报文分析程序的设计与实现(2024)
1.题目描述 在上一题的基础上,参照教材中各层报文的头部结构,结合使用 wireshark 软件(下载地址 https://www.wireshark.org/download.html#releases)观察网络各层报文捕获,解析和分析的过程(如下 图所示&a…...
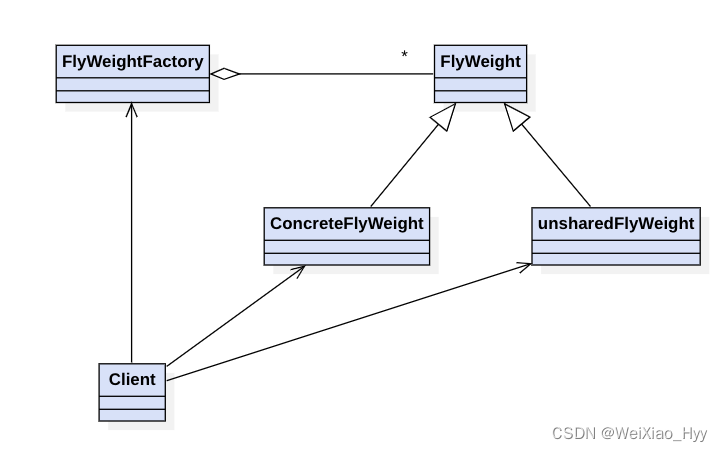
贯穿设计模式-享元模式思考
写享元模式的时候,会想使用ConcurrentHashMap来保证并发,没有使用双重锁会不会有问题?但是在synchronize代码块里面需要尽量避免throw异常,希望有经验的同学能够给出解答? 1月6号补充:没有使用双重锁会有问…...
)
牛客刷题:BC45 小乐乐改数字(中等)
自我介绍:一个脑子不好的大一学生,c语言接触还没到半年,若涉及到效率等问题,各位都可以在评论区提出见解,谢谢啦。 该账号介绍:此帐号会发布游戏(目前还只会简单小游戏),…...
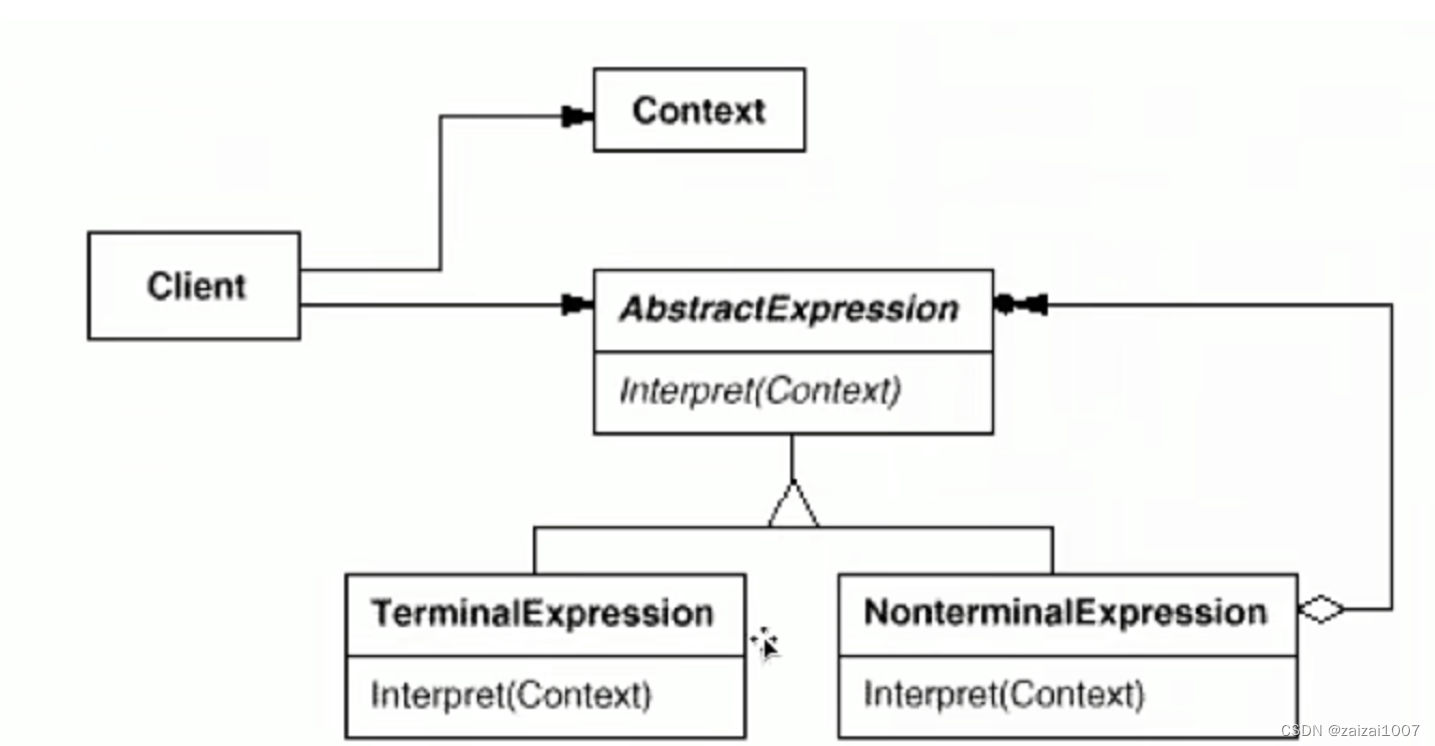
设计模式学习2
代理模式:Proxy 动机 “增加一层间接层”是软件系统中对许多复杂问题的一种常见解决方案。在面向对象系统中,直接食用某些对象会带来很多问题,作为间接层的proxy对象便是解决这一问题的常见手段。 2.伪代码: class ISubject{ pu…...

Rust:如何判断位置结构的JSON串的成员的数据类型
如何判断位置结构的JSON串的成员的数据类型,给一个Rust的例子,其中包含对数组的判断? 在Rust中,你可以使用serde_json库来处理JSON数据,并通过serde_json::Value类型的方法来判断JSON串中成员的数据类型。以下是一个示…...
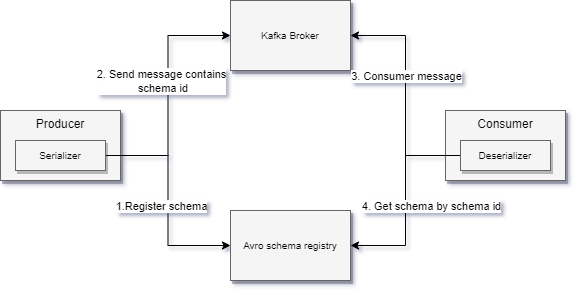
Kafka(五)生产者
目录 Kafka生产者1 配置生产者bootstrap.serverskey.serializervalue.serializerclient.id""acksallbuffer.memory33554432(32MB)compression.typenonebatch.size16384(16KB)max.in.flight.requests.per.connection5max.request.size1048576(1MB)receive.buffer.byte…...

【Leetcode】242.有效的字母异位词
一、题目 1、题目描述 给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。 注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。 示例1: 输入: s = "anagram", t = "nagaram" 输出: true示例2: 输入: …...
关系数据理论的函数依赖)
【数据库原理】(16)关系数据理论的函数依赖
一.函数依赖的概念 函数依赖是关系数据库中核心的概念,它指的是在属性集之间存在的一种特定的关系。这种关系表明,一个属性集的值可以唯一确定另一个属性集的值。 属性子集:在关系模式中,X和Y可以是单个属性,也可以是…...

脆弱的SSL加密算法漏洞原理以及修复方法
漏洞名称:弱加密算法、脆弱的加密算法、脆弱的SSL加密算法、openssl的FREAK Attack漏洞 漏洞描述:脆弱的SSL加密算法,是一种常见的漏洞,且至今仍有大量软件支持低强度的加密协议,包括部分版本的openssl。其实…...
)
SVN迁移至GitLab,并附带历史提交记录(二)
与《SVN迁移至GitLab,并附带历史提交记录》用的 git svn clone不同,本文使用svn2git来迁移项目代码。 一、准备工作 安装Git环境,配置本地git账户信息: git config --global user.name "XXX" git config --global us…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...
