当前位置： 首页 > news >正文

书生·浦语大模型趣味 Demo笔记及作业

news 2026/2/8 8:50:44

文章目录

  • 笔记
  • 作业
    • 基础作业：
    • 进阶作业：

笔记

  • 书生·浦语大模型InternLM-Chat-7B 智能对话 Demo：https://blog.csdn.net/m0_49289284/article/details/135412067
  • 书生·浦语大模型Lagent 智能体工具调用 Demo：https://blog.csdn.net/m0_49289284/article/details/135426100

作业

基础作业：

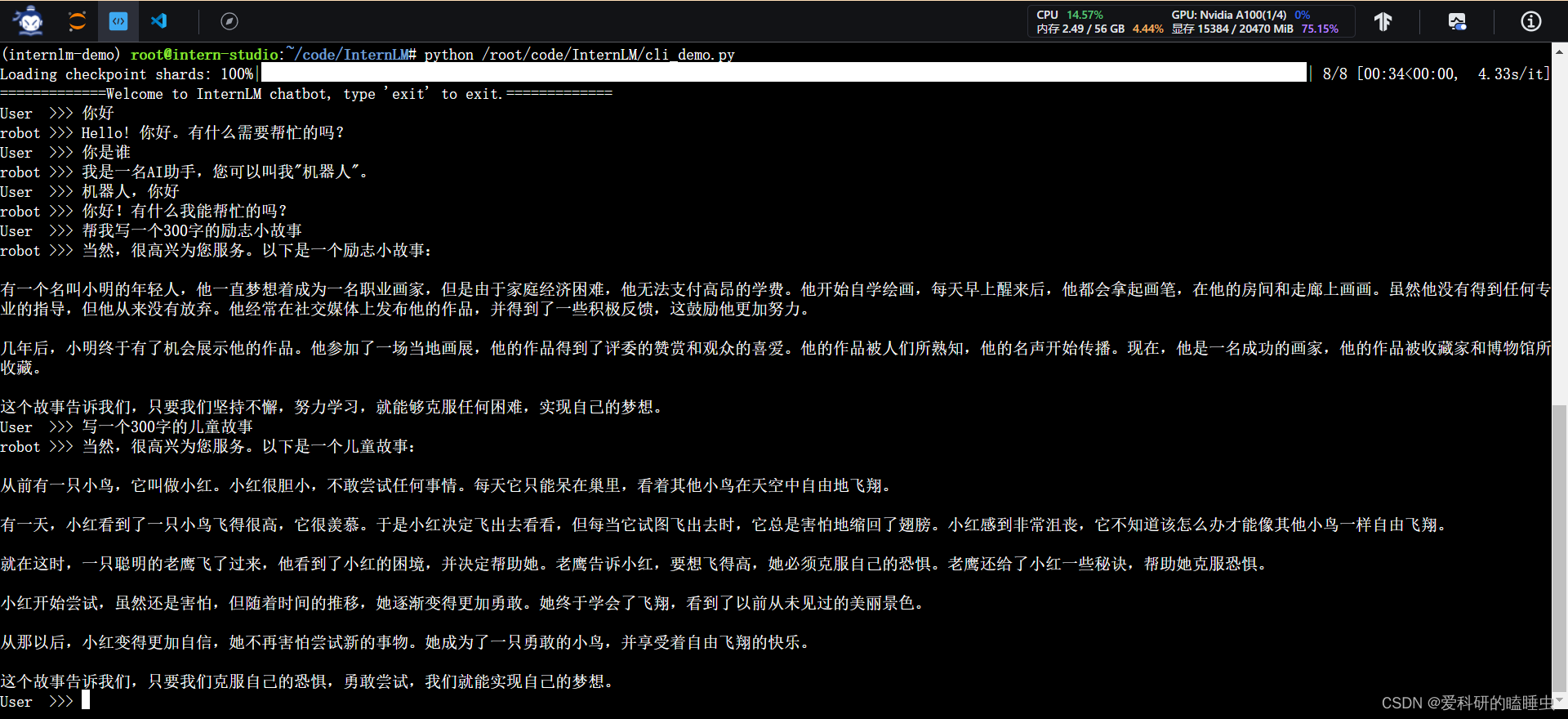
  • 使用 InternLM-Chat-7B 模型生成 300 字的小故事
    在这里插入图片描述
  • 使用 huggingface_hub python 包，下载 InternLM-20B 的 config.json 文件到本地
    在这里插入图片描述

进阶作业：

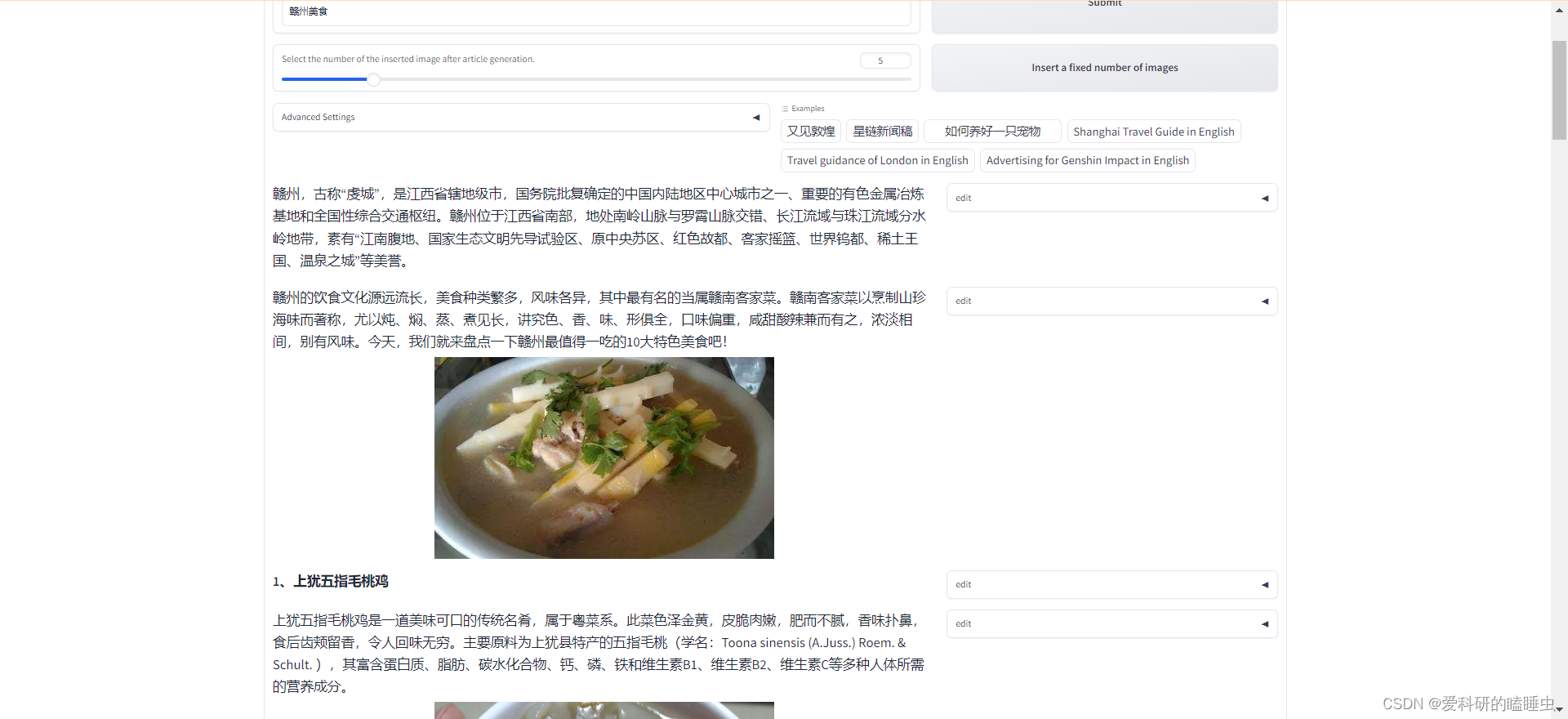
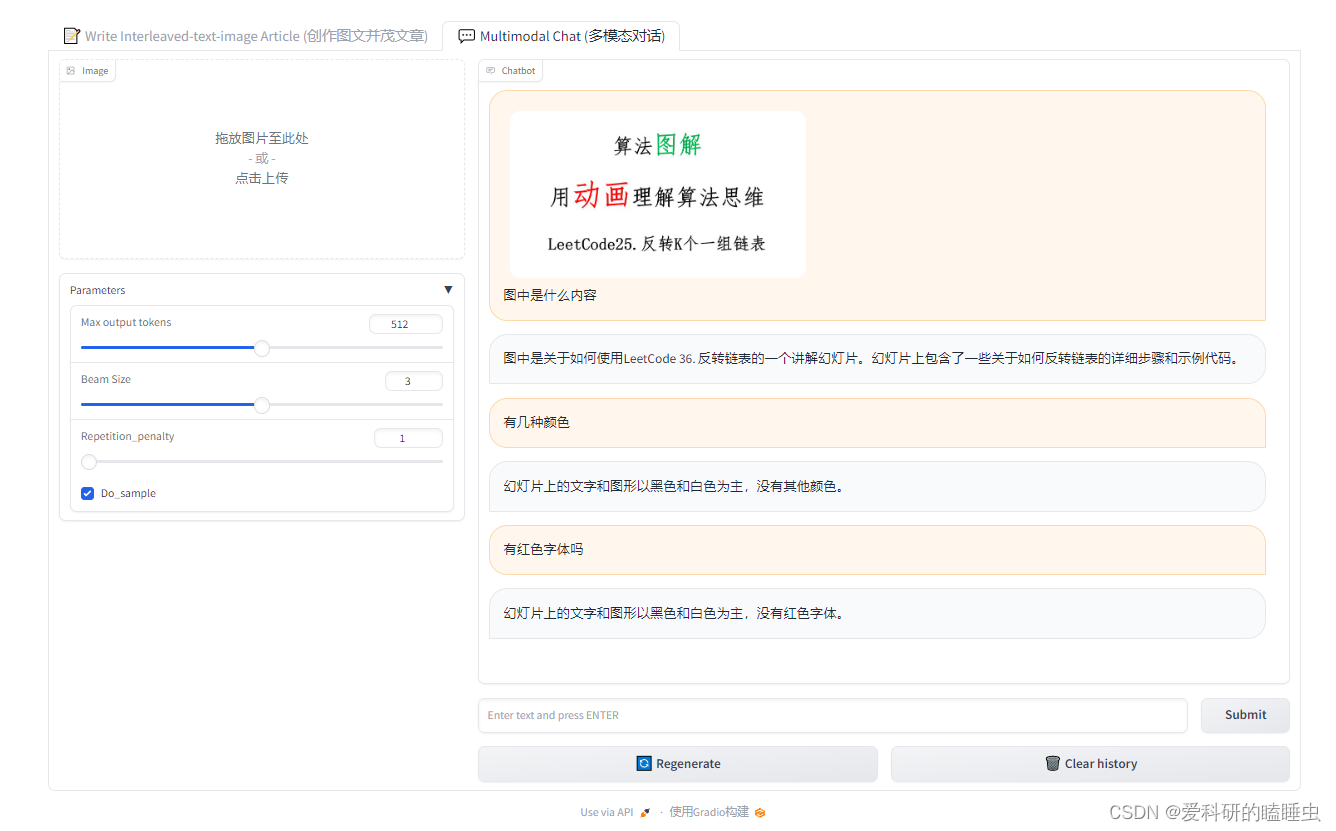
  • 浦语·灵笔的图文理解及创作部署
    请添加图片描述
    请添加图片描述

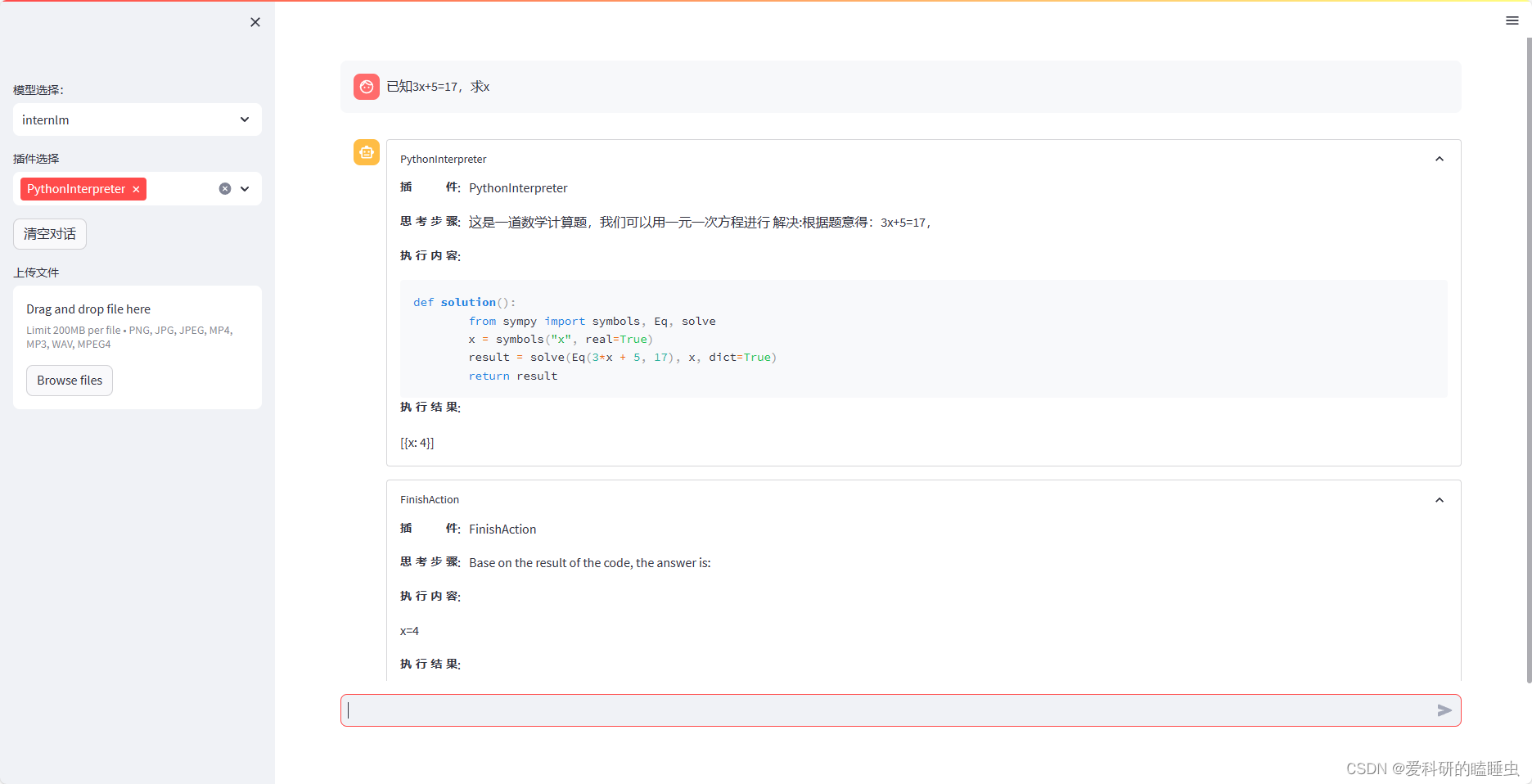
  • Lagent 工具调用 Demo 创作部署
    请添加图片描述

相关文章：

书生·浦语大模型趣味 Demo笔记及作业

文章目录 笔记作业基础作业：进阶作业： 笔记 书生浦语大模型InternLM-Chat-7B 智能对话 Demo：https://blog.csdn.net/m0_49289284/article/details/135412067书生浦语大模型Lagent 智能体工具调用 Demo：https://blog.csdn.net/m0_…...

编程日记 2024/1/9 4:35:06

2024最新前端源码分享（附效果图及在线演示）

分享10款非常有趣的前端特效源码 其中包含css动画特效、js原生特效、svg特效以及小游戏等 下面我会给出特效样式图或演示效果图 但你也可以点击在线预览查看源码的最终展示效果及下载源码资源 粒子文字动画特效 基于canvas实现的粒子文字动画特效 会来回切换设定的文字特效 图…...

编程日记 2024/1/9 4:32:04

Microsoft 365 for Mac激活版(原Office 365)

Microsoft 365 for Mac原office 365，包含Word、Excel、PowerPoint 和 Outlook应用程序，协作办公的最佳首选。 软件下载：Microsoft 365 for Mac激活版下载 Microsoft 365 的一些主要功能包括： office 应用程序：Microsof…...

编程日记 2024/1/9 4:31:03

快乐学Python，Python基础之组织代码「类与对象」

在上一篇文章中，我们了解了函数。这一篇文章我们来了解一下Python中另外一个重要的概念：类与对象。 1、类与对象 （1）类与对象有什么关系？ 你可能会奇怪，为什么要叫类与对象呢？是两个不同的东…...

编程日记 2024/1/9 4:30:02

H5的3D游戏开源框架

在H5的3D游戏框架中，Three.js、Babylon.js和Turbulenz是比较受欢迎的选择。 Three.js是一个广泛应用并且功能强大的JavaScript 3D库，可以创建简单的3D动画到创建交互的3D游戏。 Babylon.js是David Catuhe对3D游戏引擎热爱的结果，是最好的Ja…...

编程日记 2024/1/9 4:29:01

浅谈一些生命周期

vue2生命周期 beforeCreate ：实例创建之初 created：组件已经创建完成 beforeMount：组件挂载之前 mounted:组件挂载之后 beforeUpdate：数据发生变化 更新之前 undated：数据发生之后 beforeDestroy ：实…...

编程日记 2024/1/9 4:21:56

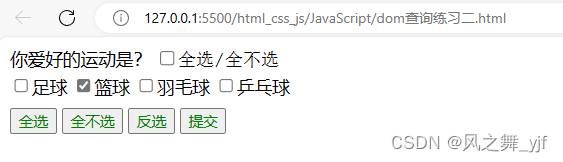
JavaScript基础(25)_dom查询练习（二）

<!DOCTYPE html> <html lang"zh"> <head><meta charset"UTF-8"><title>dom查询练习二</title><link rel"stylesheet" href"../browser_default_style/reset.css"><style>form {margi…...

编程日记 2024/1/9 4:19:53

【React系列】React生命周期、setState深入理解、 shouldComponentUpdate和PureComponent性能优化、脚手架

本文来自#React系列教程&#xff1a;https://mp.weixin.qq.com/mp/appmsgalbum?__bizMzg5MDAzNzkwNA&actiongetalbum&album_id1566025152667107329) 一. 生命周期 1.1. 认识生命周期 很多的事物都有从创建到销毁的整个过程&#xff0c;这个过程称之为是生命周期&…...

编程日记 2024/1/9 4:18:52

一文初步了解slam技术

本文初步介绍slam技术&#xff0c;主要是slam技术的概述&#xff0c;涉及技术原理、应用场景、分类、以及各自优缺点&#xff0c;和slam技术的未来展望。 &#x1f3ac;个人简介&#xff1a;一个全栈工程师的升级之路&#xff01; &#x1f4cb;个人专栏&#xff1a;slam精进之…...

编程日记 2024/1/9 4:17:51

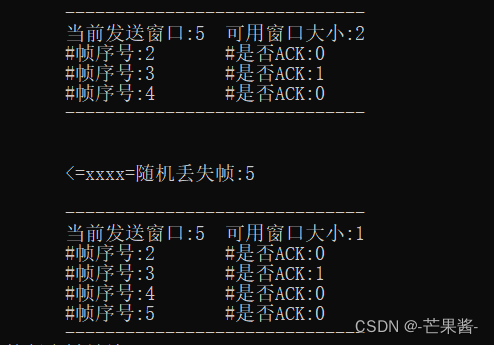
滑动窗口协议仿真（2024）

1.题目描述 滑动窗口协议以基于分组的数据传输协议为特征&#xff0c;该协议适用于在数据链路层以及传输层中对按 顺序传送分组的可靠性要求较高的环境。在长管道传输过程&#xff08;特别是无线环境&#xff09;中&#xff0c;相应的滑动窗口 协议可实现高效的重传恢复。附录 …...

编程日记 2024/1/9 4:15:50

uniapp上传文件时用到的api是什么？格式是什么？

在UniApp中&#xff0c;你可以使用uni.uploadFile()方法来上传文件。这是一个异步方法&#xff0c;用于将本地资源上传到服务器。 该方法的基本格式如下&#xff1a; uni.uploadFile({url: 上传接口地址,filePath: 要上传的文件路径,name: 后端接收的文件参数名,formData: {/…...

编程日记 2024/1/9 4:14:48

Java面试——框架篇

1、Spring框架中的单例bean是线程安全的吗&#xff1f; 所谓单例就是所有的请求都用一个对象来处理&#xff0c;而多例则指每个请求用一个新的对象来处理。 结论&#xff1a;线程不安全。 Spring框架中有一个Scope注解&#xff0c;默认的值就是singleton&#xff0c;单例的。一…...

编程日记 2024/1/9 4:12:46

GO语言笔记1-安装与hello world

SDK开发工具包下载 Go语言官网地址&#xff1a;golang.org&#xff0c;无法访问Golang中文社区&#xff1a;首页 - Go语言中文网 - Golang中文社区下载地址&#xff1a;Go下载 - Go语言中文网 - Golang中文社区 尽量去下载稳定版本&#xff0c;根据使用系统下载压缩包格式的安装…...

编程日记 2024/1/9 4:08:44

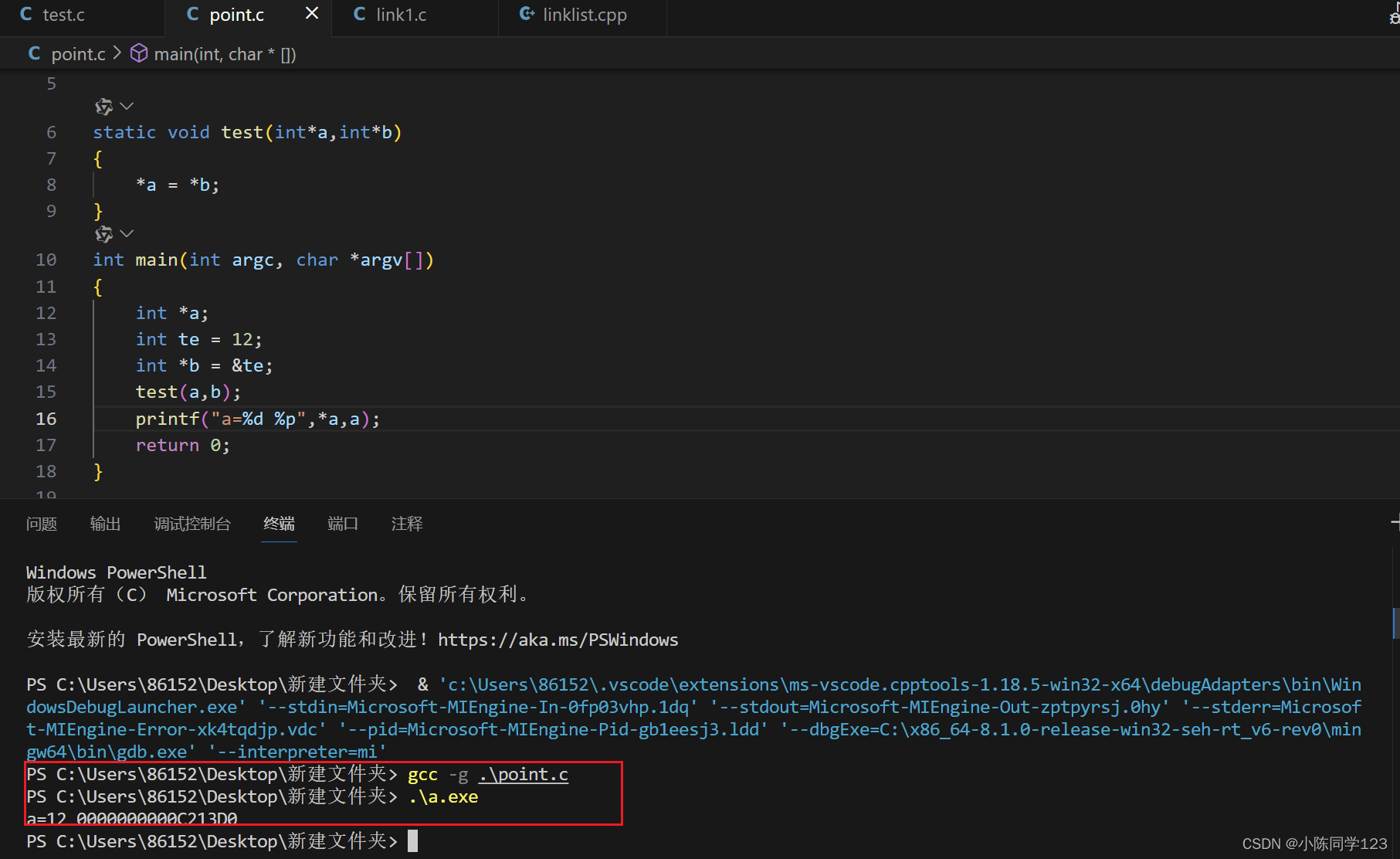
指针传参误区

C语言中指针作为形参传递时&#xff0c;func&#xff08;*a, *b&#xff09; 这种形式的话&#xff0c;是无法通过简单的 ab来修改的&#xff0c;在函数体内a的地址确实被修改成b的地址了&#xff0c;但是当函数执行结束时&#xff0c;a的地址会重新回到原本的地址里面&#xf…...

编程日记 2024/1/9 4:07:43

力扣-42.接雨水

题目&#xff1a; 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图&#xff0c;计算按此排列的柱子&#xff0c;下雨之后能接多少雨水。 示例 1&#xff1a; 输入&#xff1a;height [0,1,0,2,1,0,1,3,2,1,2,1] 输出&#xff1a;6 解释&#xff1a;上面是由数组[0,1,0,2…...

编程日记 2024/1/9 4:05:40

LeetCode-移动零（283）

题目描述&#xff1a; 给定一个数组 nums&#xff0c;编写一个函数将所有 0 移动到数组的末尾&#xff0c;同时保持非零元素的相对顺序。 请注意 &#xff0c;必须在不复制数组的情况下原地对数组进行操作。 思路&#xff1a; 这里的思路跟以前做过的去重复数字的思路有点像&…...

编程日记 2024/1/9 4:04:39

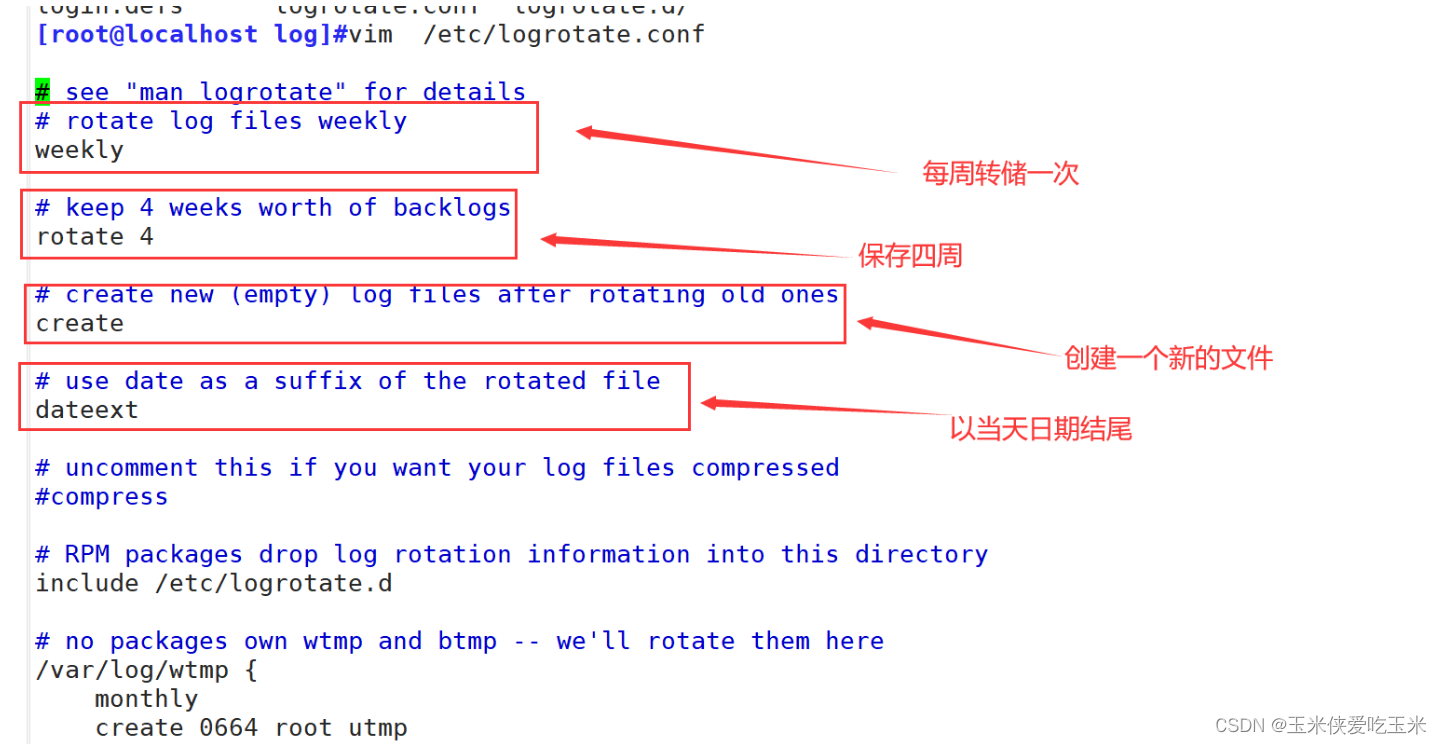
文件系统与日志分析

一&#xff0c;文件系统 &#xff08;一&#xff09;inode 和block概述 1&#xff0c;文件数据包括元信息与实际数据 2&#xff0c;文件存储在硬盘上&#xff0c;硬盘最小存储单位是“扇区”&#xff0c;每个扇区存储512字节 3&#xff0c;block (块) 连续的八个扇区组成一…...

编程日记 2024/1/9 4:01:37

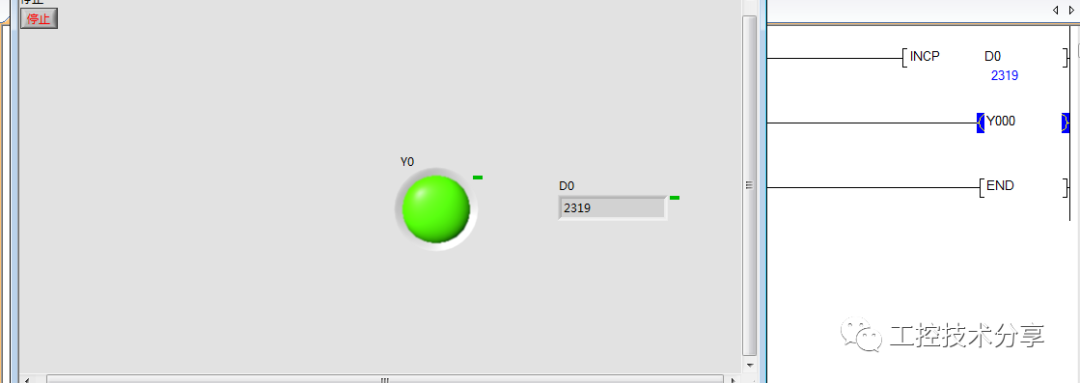
labview 与三菱FX 小型PLC通信(OPC)

NI OPC服务器与三菱FX3U PLC通讯方法 一、新建通道名称为&#xff1a;MIT 二、选择三菱FX系列 三、确认端口号相关的参数&#xff08;COM端&#xff1a;7.波特率&#xff1a;9600&#xff0c;数据位&#xff1a;7&#xff0c;校验&#xff1a;奇校验&#xff0c;停止位&#xf…...

编程日记 2024/1/9 4:00:36

掌握Linux网络配置：价格亲民，操作简便！

前言 在Linux系统中&#xff0c;网络配置是实现连接、通信和安全的重要一环。无论你是初学者还是有经验的用户&#xff0c;掌握网络配置命令能帮助你轻松管理网络接口、设置IP地址以及查看连接状态。以下是一些关键命令和示例&#xff0c;让你快速掌握网络操作的精髓&#xff…...

编程日记 2024/1/9 3:56:32

郑州大学算法设计与分析实验2

判断题 1 #include<bits/stdc.h> using namespace std;const int N 50; int f[N], n;int main() { // freopen("1.in", "r", stdin);ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin >> n;f[1] 1; f[2] 1;for(int i 3; i &l…...

编程日记 2024/1/9 3:55:30

uniapp 对接腾讯云IM群组成员管理（增删改查）

UniApp 实战&#xff1a;腾讯云IM群组成员管理&#xff08;增删改查&#xff09; 一、前言 在社交类App开发中&#xff0c;群组成员管理是核心功能之一。本文将基于UniApp框架&#xff0c;结合腾讯云IM SDK&#xff0c;详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

编程新知 2026/1/13 9:59:27

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八

现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet&#xff0c;点击确认后如下提示 最终上报fail 解决方法 内核升级导致&#xff0c;需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

编程新知 2026/1/24 10:07:40

蓝牙 BLE 扫描面试题大全(2)：进阶面试题与实战演练

前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1)&#xff1a;从基础到实战的深度解析-CSDN博客&#xff0c;但实际面试中&#xff0c;企业更关注候选人对复杂场景的应对能力&#xff08;如多设备并发扫描、低功耗与高发现率的平衡&#xff09;和前沿技术的…...

编程新知 2026/2/5 3:41:42

相机从app启动流程

一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下： 重点代码分析： 启动相机前，先要通过getCameraIdList获取camera的个数以及id，然后可以通过getCameraCharacteristics获取对应id camera的capabilities（静态信息）进行一些openCamera前的…...

编程新知 2026/1/31 5:09:19

【Oracle】分区表

个人主页&#xff1a;Guiat 归属专栏&#xff1a;Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

编程新知 2026/1/20 21:59:36

今日学习：Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存

文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

编程新知 2026/1/27 16:41:02

html css js网页制作成品——HTML+CSS榴莲商城网页设计（4页）附源码

目录 一、&#x1f468;‍&#x1f393;网站题目 二、✍️网站描述 三、&#x1f4da;网站介绍 四、&#x1f310;网站效果 五、&#x1fa93; 代码实现 &#x1f9f1;HTML 六、&#x1f947; 如何让学习不再盲目 七、&#x1f381;更多干货 一、&#x1f468;‍&#x1f…...

编程新知 2026/2/7 22:17:30

WebRTC从入门到实践 - 零基础教程

WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC&#xff1f; WebRTC&#xff08;Web Real-Time Communication&#xff09;是一个支持网页浏览器进行实时语音…...

编程新知 2026/1/5 0:33:43

Kafka主题运维全指南：从基础配置到故障处理

#作者&#xff1a;张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1&#xff1a;主题删除失败。常见错误2&#xff1a;__consumer_offsets占用太多的磁盘。 主题日常管理 …...

编程新知 2025/6/10 21:14:43

多元隐函数 偏导公式

我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式&#xff0c;给定一个隐函数关系&#xff1a; F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 &#x1f9e0; 目标&#xff1a; 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z​、 …...

编程新知 2025/9/19 5:31:38