复试 || 就业day05(2024.01.08)项目一
文章目录
- 前言
- 代码模拟梯度下降
- 构建函数与导函数
- 函数的可视化
- 求这个方程的最小值(直接求导)
- 求方程最小值(不令方程导为0)【梯度下降】
- eta=0.1
- eta = 0.2
- eta = 50
- eta = 0.01
- 画出eta=0.1时的梯度下降x的变化过程
- 总结
前言
💫你好,我是辰chen,本文旨在准备考研复试或就业
💫本文内容来自某机构网课,是我为复试准备的第一个项目
💫欢迎大家的关注,我的博客主要关注于考研408以及AIoT的内容
🌟 预置知识详见我的AIoT板块,需掌握 基本Python语法, Numpy, Pandas, Matplotlib
以下的几个专栏是本人比较满意的专栏(大部分专栏仍在持续更新),欢迎大家的关注:
💥ACM-ICPC算法汇总【基础篇】
💥ACM-ICPC算法汇总【提高篇】
💥AIoT(人工智能+物联网)
💥考研
💥CSP认证考试历年题解
代码模拟梯度下降
import numpy as np
import matplotlib.pyplot as plt
构建函数与导函数
f = lambda x : (x - 3.5) ** 2 - 4.5 * x + 10
# 导函数
g = lambda x : 2 * (x - 3.5) - 4.5
函数的可视化
x = np.linspace(0, 11.5, 100)
y = f(x)plt.plot(x, y)
# 画出最小值点(5.75即为最小值点,具体计算即为令导数为0,见下个代码块)
plt.scatter(5.75, f(5.75), color = 'red', s = 30)
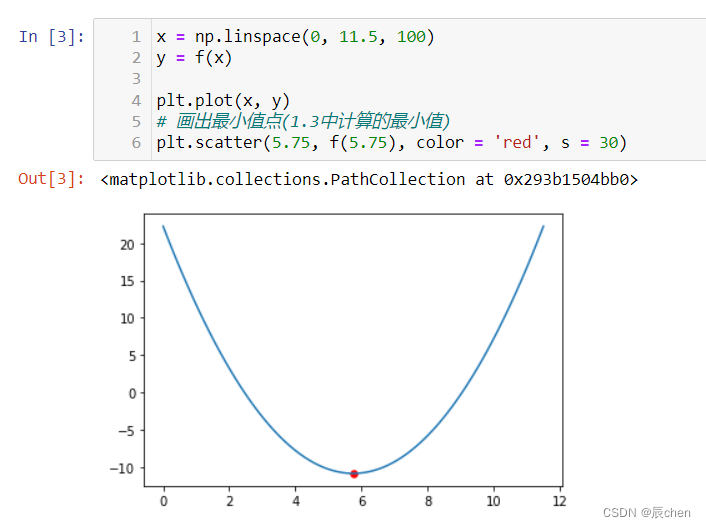
求这个方程的最小值(直接求导)
'''
令导数值 = 0
2 * (x - 3.5) - 4.5 = 0
2 * x = 11.5
x = 5.75
'''
求方程最小值(不令方程导为0)【梯度下降】
eta=0.1
# 给一个步幅,也就是学习率
eta = 0.1 # 正解为 x = 5.75, 若我们梯度下降求得的 x = 5.749, 5.7501 ... 亦是正确答案(很接近)
x = np.random.randint(0, 12, size = 1)[0]# 多次 while 循环,每次梯度下降,记录一下上一次的值,规定一个精确度进行比较
# +0.1; +0.2; +1;...都是可以的,是为了让他们在一开始有差异
last_x = x + 0.1# 下面自定义一个精确度
precision = 0.0001
print('-----------------随机的x是:', x)while True:if np.abs(x - last_x) < precision: # 退出死循环条件:更新时变化甚微break# 更新,梯度下降last_x = xx = x - eta * g(x)print('+++++++++++++++++更新之后的x是:', x)
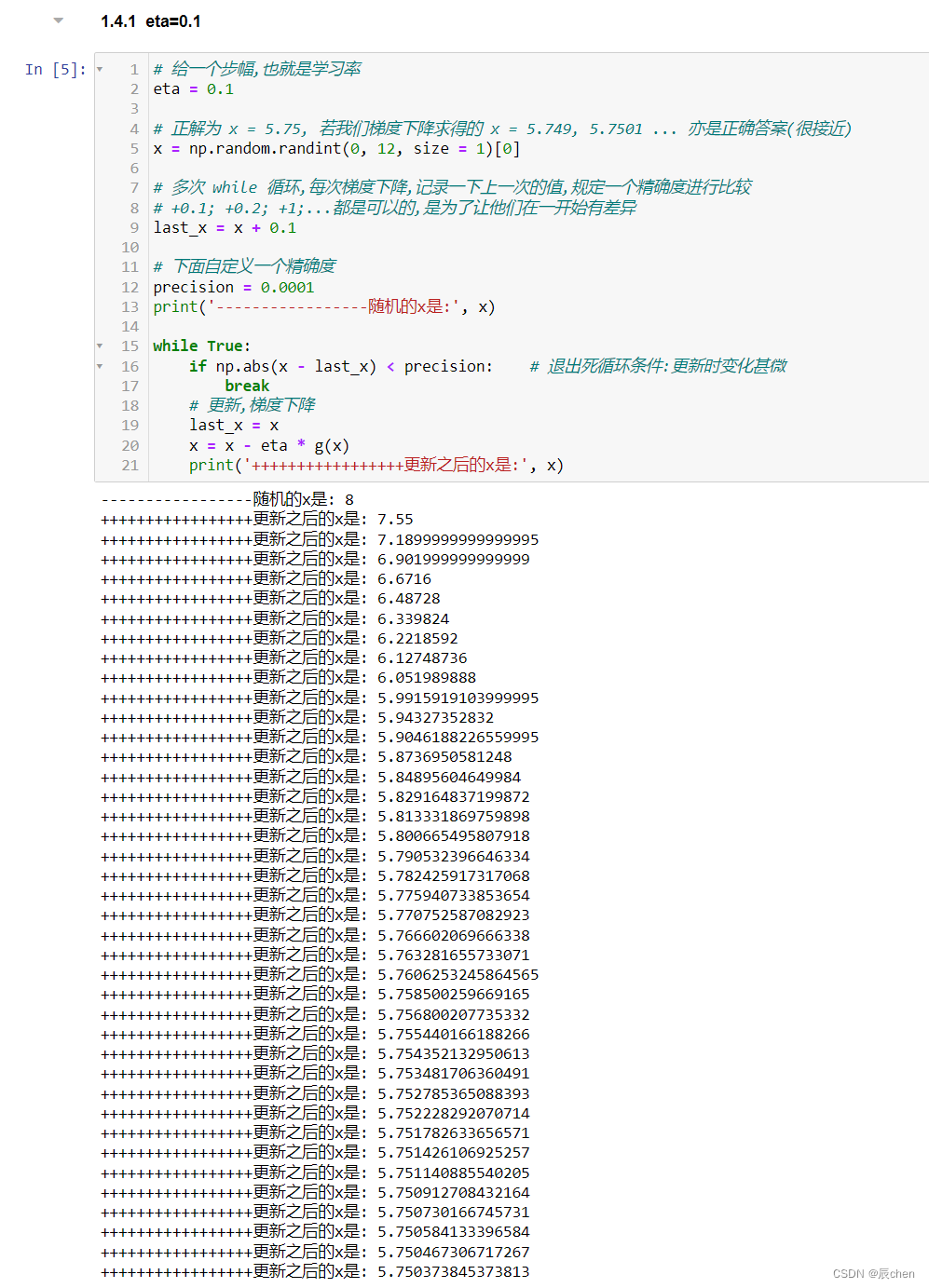
可以看到,最终逼近的结果为 5.750373845373813,可以认为是正确解
eta = 0.2
把 eta 调大之后,可以明显观察到收敛的快了
# 给一个步幅,也就是学习率
eta = 0.2# 正解为 x = 5.75, 若我们梯度下降求得的 x = 5.749, 5.7501 ... 亦是正确答案(很接近)
x = np.random.randint(0, 12, size = 1)[0]# 多次 while 循环,每次梯度下降,记录一下上一次的值,规定一个精确度进行比较
# +0.1; +0.2; +1;...都是可以的,是为了让他们在一开始有差异
last_x = x + 0.1# 下面自定义一个精确度
precision = 0.0001
print('-----------------随机的x是:', x)while True:if np.abs(x - last_x) < precision: # 退出死循环条件:更新时变化甚微break# 更新,梯度下降last_x = xx = x - eta * g(x)print('+++++++++++++++++更新之后的x是:', x)
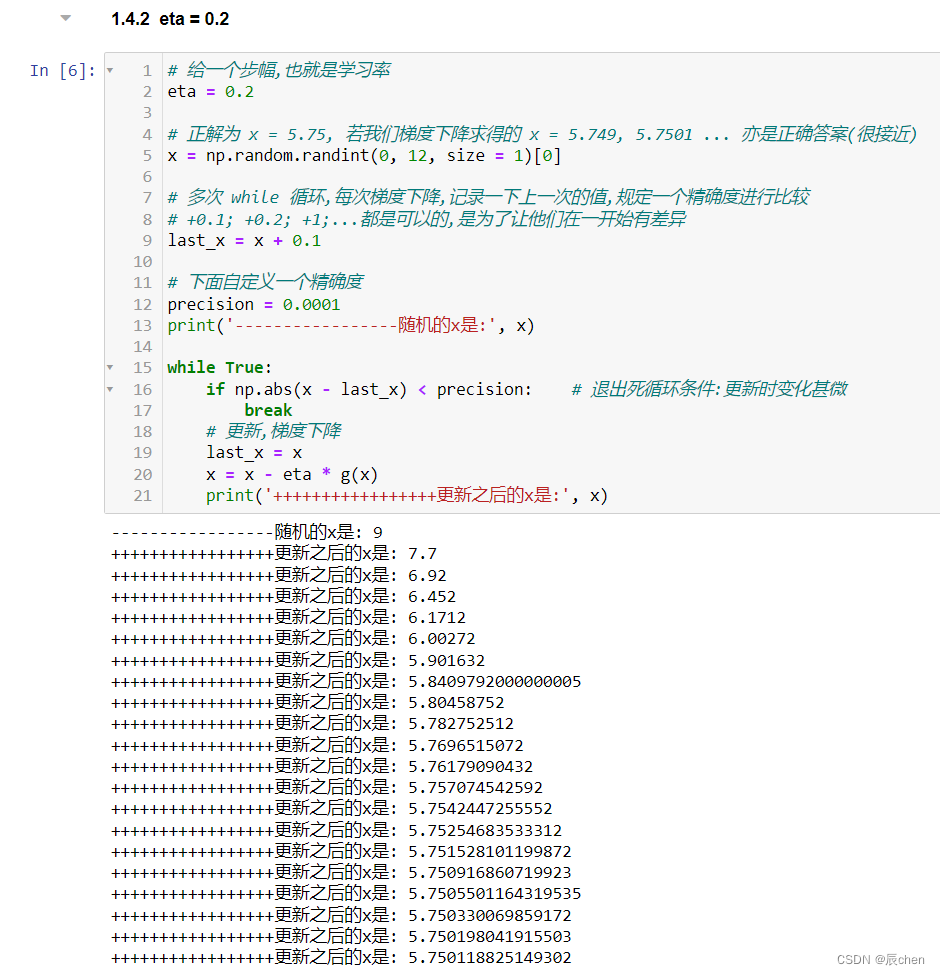
eta = 50
当然,eta 的值也不可以设的过大,会造成发散
# 给一个步幅,也就是学习率
eta = 50# 正解为 x = 5.75, 若我们梯度下降求得的 x = 5.749, 5.7501 ... 亦是正确答案(很接近)
x = np.random.randint(0, 12, size = 1)[0]# 多次 while 循环,每次梯度下降,记录一下上一次的值,规定一个精确度进行比较
# +0.1; +0.2; +1;...都是可以的,是为了让他们在一开始有差异
last_x = x + 0.1# 下面自定义一个精确度
precision = 0.0001
print('-----------------随机的x是:', x)while True:if np.abs(x - last_x) < precision: # 退出死循环条件:更新时变化甚微break# 更新,梯度下降last_x = xx = x - eta * g(x)print('+++++++++++++++++更新之后的x是:', x)
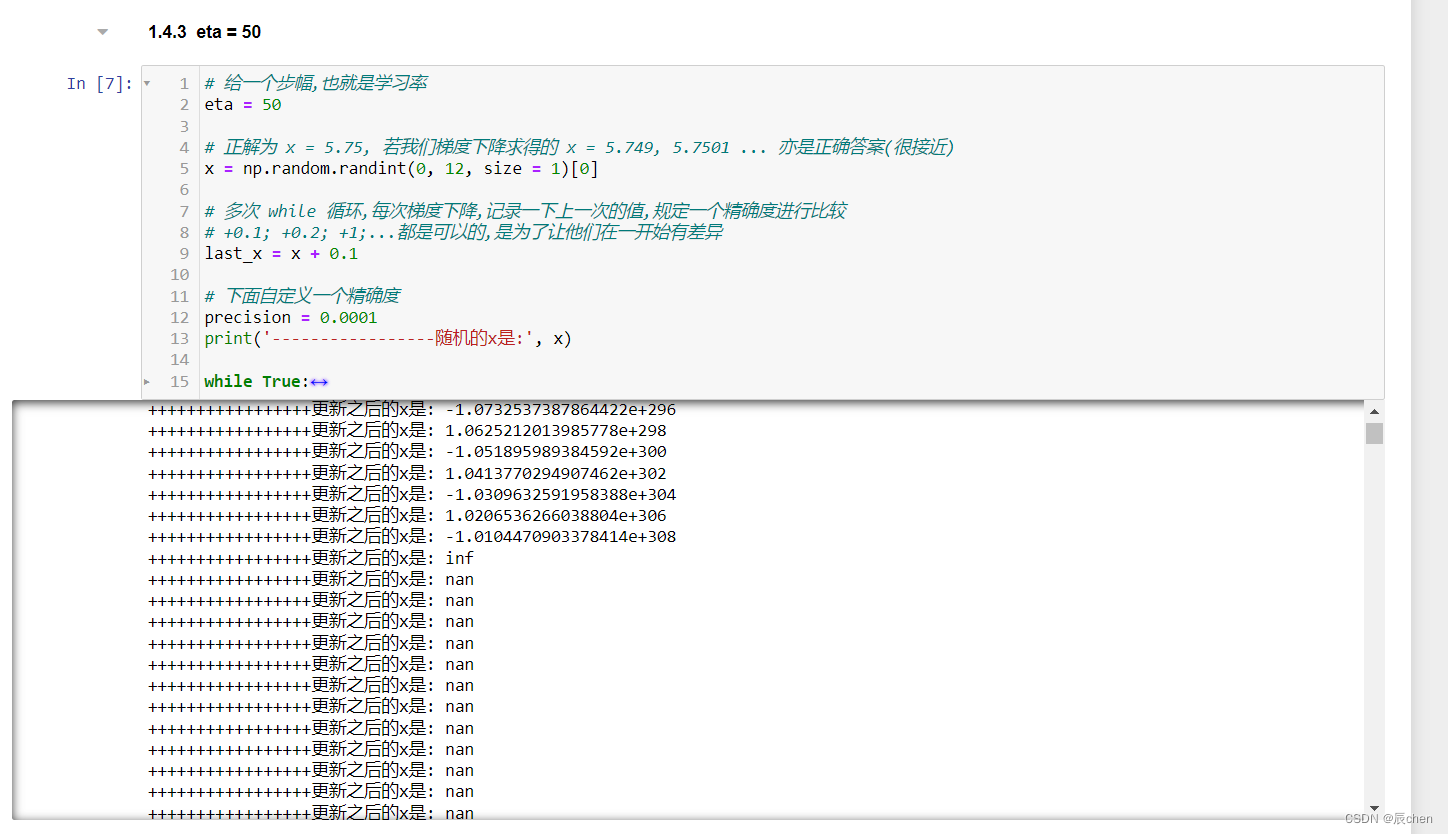
这是一个死循环
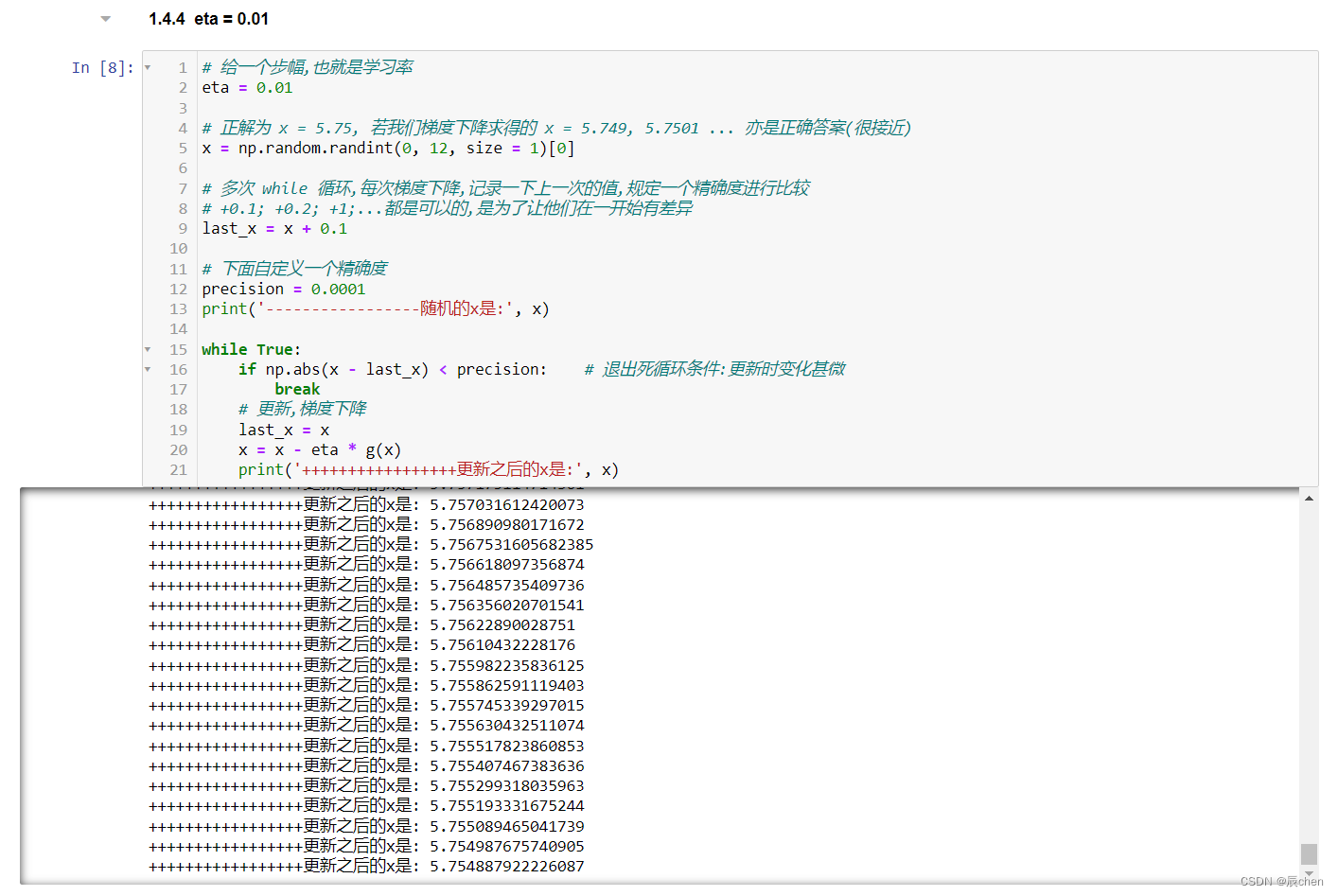
eta = 0.01
如果 eta 的值设的比较小,会收敛,但是会很慢
# 给一个步幅,也就是学习率
eta = 0.01# 正解为 x = 5.75, 若我们梯度下降求得的 x = 5.749, 5.7501 ... 亦是正确答案(很接近)
x = np.random.randint(0, 12, size = 1)[0]# 多次 while 循环,每次梯度下降,记录一下上一次的值,规定一个精确度进行比较
# +0.1; +0.2; +1;...都是可以的,是为了让他们在一开始有差异
last_x = x + 0.1# 下面自定义一个精确度
precision = 0.0001
print('-----------------随机的x是:', x)while True:if np.abs(x - last_x) < precision: # 退出死循环条件:更新时变化甚微break# 更新,梯度下降last_x = xx = x - eta * g(x)print('+++++++++++++++++更新之后的x是:', x)
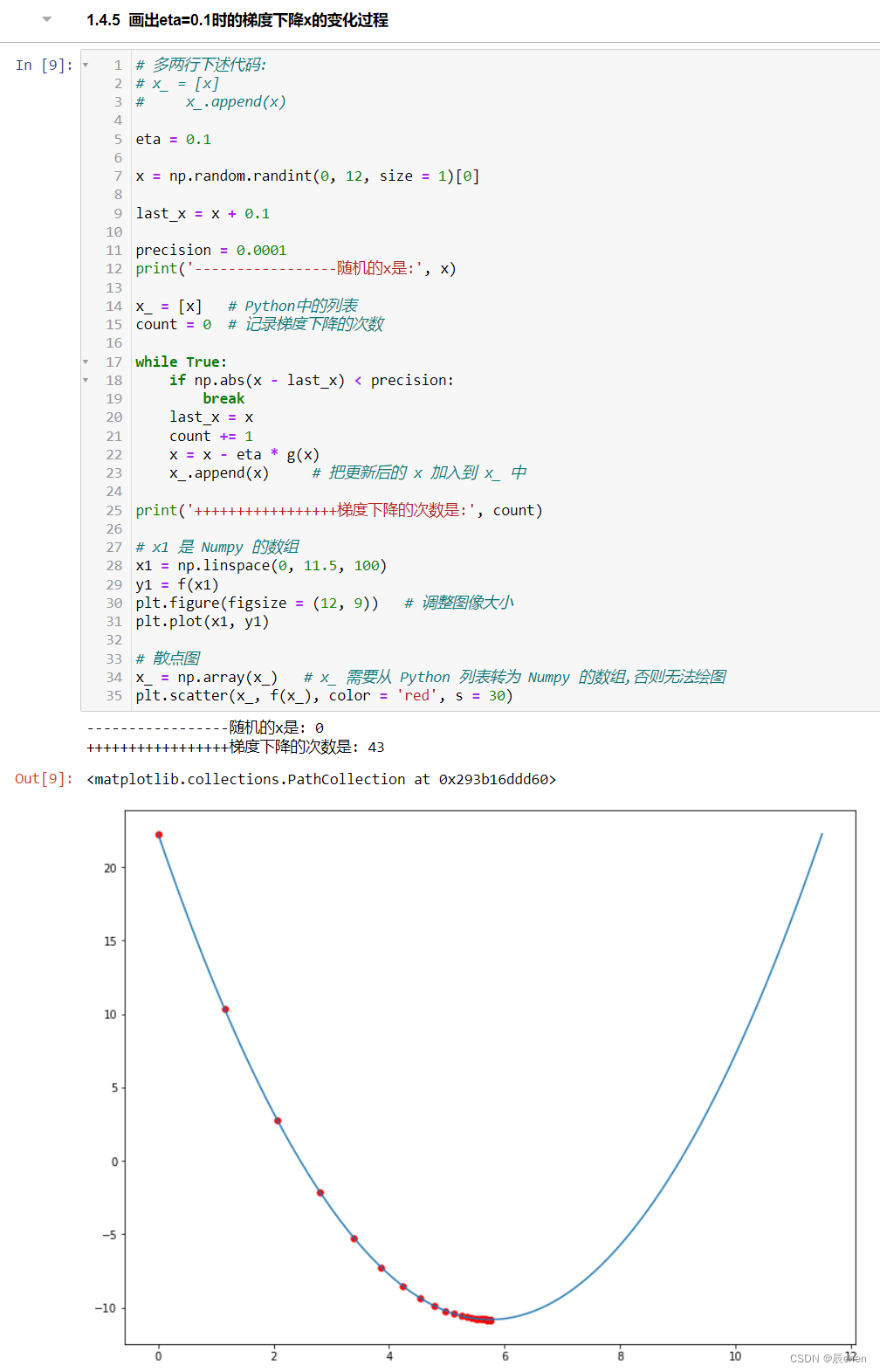
画出eta=0.1时的梯度下降x的变化过程
# 多两行下述代码:
# x_ = [x]
# x_.append(x)eta = 0.1 x = np.random.randint(0, 12, size = 1)[0]last_x = x + 0.1precision = 0.0001
print('-----------------随机的x是:', x)x_ = [x] # Python中的列表
count = 0 # 记录梯度下降的次数while True:if np.abs(x - last_x) < precision: breaklast_x = xcount += 1x = x - eta * g(x)x_.append(x) # 把更新后的 x 加入到 x_ 中print('+++++++++++++++++梯度下降的次数是:', count)# x1 是 Numpy 的数组
x1 = np.linspace(0, 11.5, 100)
y1 = f(x1)
plt.figure(figsize = (12, 9)) # 调整图像大小
plt.plot(x1, y1)# 散点图
x_ = np.array(x_) # x_ 需要从 Python 列表转为 Numpy 的数组,否则无法绘图
plt.scatter(x_, f(x_), color = 'red', s = 30)
总结
模拟的时候还发现了 eta 设置的过小算出来的值也是错误的现象,知道了原因后会补在这里

相关文章:

复试 || 就业day05(2024.01.08)项目一
文章目录 前言代码模拟梯度下降构建函数与导函数函数的可视化求这个方程的最小值(直接求导)求方程最小值(不令方程导为0)【梯度下降】eta0.1eta 0.2eta 50eta 0.01画出eta0.1时的梯度下降x的变化过程 总结 前言 💫你…...

基于商品列表的拖拽排序后端实现
目录 一:实现思路 二:实现步骤 二:实现代码 三:注意点 一:实现思路 后台实现拖拽排序通常需要与前端进行配合,对商品的列表拖拽排序,前端需要告诉后端拖拽的元素和拖动的位置。 这里我们假…...
小游戏实战丨基于PyGame的贪吃蛇小游戏
文章目录 写在前面PyGame贪吃蛇注意事项系列文章写在后面 写在前面 本期内容:基于pygame的贪吃蛇小游戏 下载地址:https://download.csdn.net/download/m0_68111267/88700188 实验环境 python3.11及以上pycharmpygame 安装pygame的命令:…...
AOP(面向切面编程)基于XML方式配置
概念解释:(理解基本概念方可快速入手) 连接点(joinpoint) 被拦截到的点,因为Spring只支持方法类型的连接点,所以在Spring中连接点指的就是被拦截到的方法。 切入点(pointcut&#x…...
多线程的概念
多线程 同时执行多个任务,例如一个人一边听歌,一边跳舞 继承Thread类实现多线程的方式 定义一个MyThread类继承Thread类,重写里面的run方法 package com.itxs.demo01;/*** Classname : MyThread* Description : TODO 自定义线程继承Thread类*…...
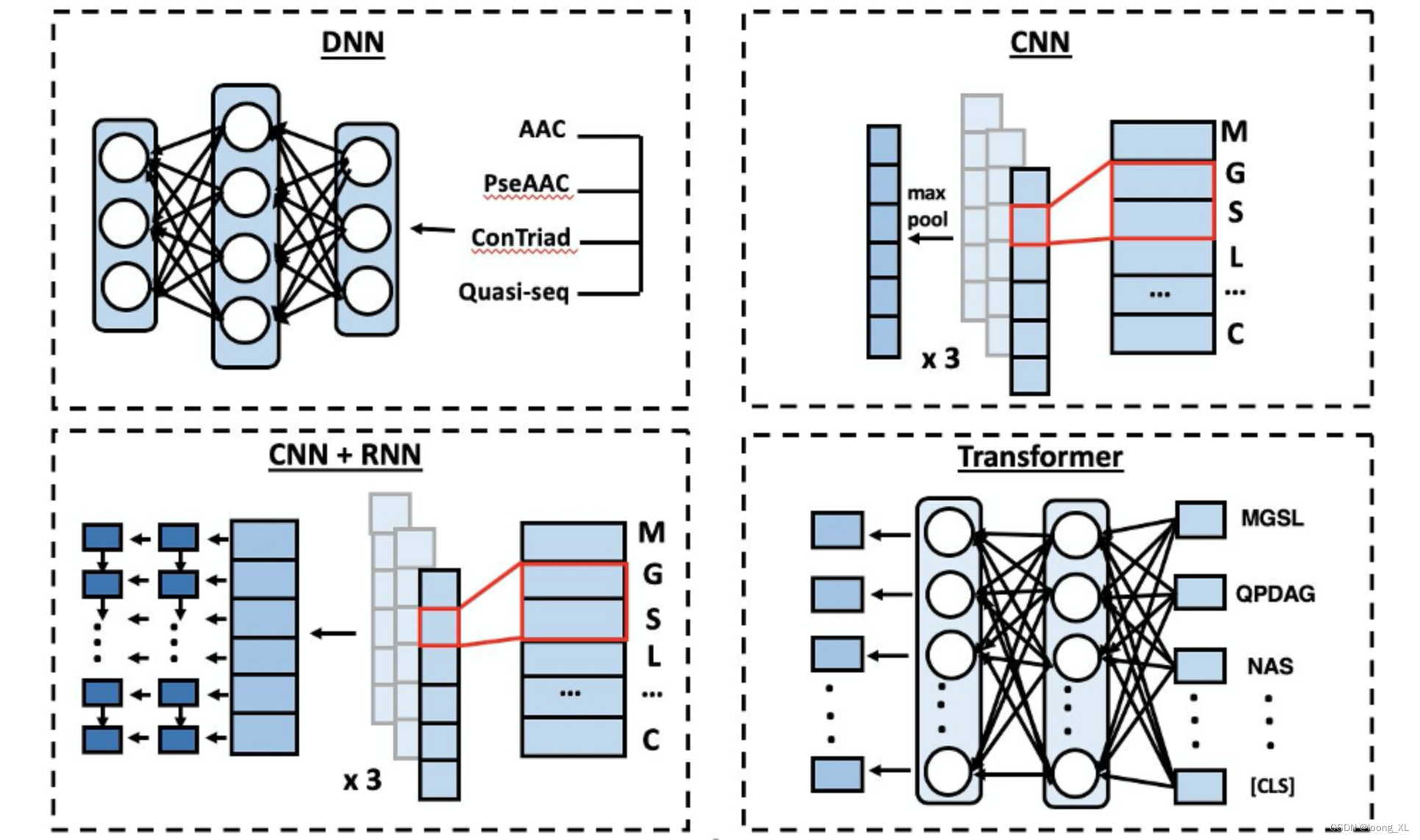
DeepPurpose 生物化学深度学习库;蛋白靶点小分子药物对接亲和力预测虚拟筛选
参考: https://blog.csdn.net/c9Yv2cf9I06K2A9E/article/details/107649770 https://github.com/kexinhuang12345/DeepPurpose ##安装 pip install DeepPurpose rdkitDeepPurpose包括: 数据: 关联TDC库下载,是同一作者开发的 https://blog.csdn.net/weixin_42357472/artic…...

Java实现责任链模式
责任链模式是一种设计模式,用于处理请求的解耦。在责任链模式中,多个对象都有机会处理请求,从而避免了请求发送者和接收者之间的直接依赖关系。每个处理者都可以决定是否处理请求以及将请求传递给下一个处理者。 简介 责任链模式由一条链组…...
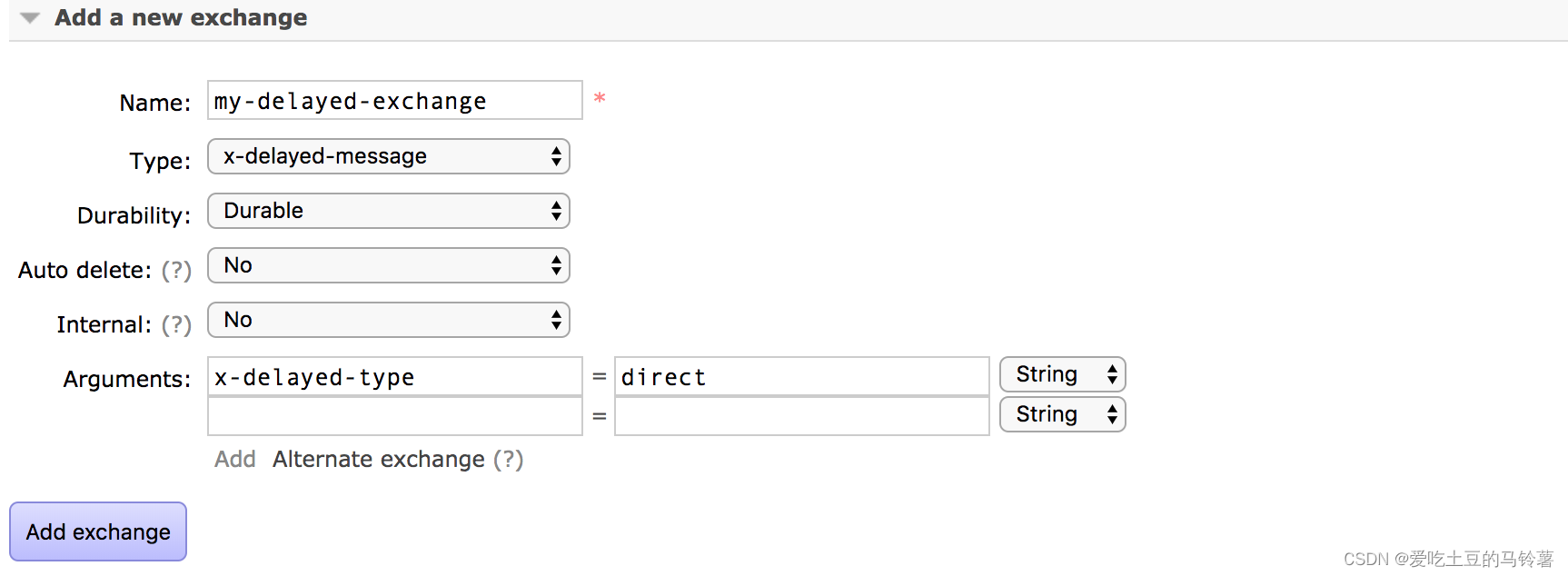
rabbitmq延时队列相关配置
确保 RabbitMQ 的延时消息插件已经安装和启用。你可以通过执行以下命令来安装该插件: rabbitmq-plugins enable rabbitmq_delayed_message_exchange 如果提示未安装,以下是安装流程: 查看mq版本: 查看自己使用的 MQ(…...

【工具】推荐一个好用的代码画图工具
PlantUML 官网地址:https://plantuml.com/zh/ 跳转 支持各种结构化数据画图支持代码调用jar包生成图片 提供在线画图能力 https://www.plantuml.com/plantuml/uml/SyfFKj2rKt3CoKnELR1Io4ZDoSa70000 有兴趣可以尝试下 over~~...
)
Leetcode14-判断句子是否为全字母句(1832)
1、题目 全字母句 指包含英语字母表中每个字母至少一次的句子。 给你一个仅由小写英文字母组成的字符串 sentence ,请你判断 sentence 是否为 全字母句 。 如果是,返回 true ;否则,返回 false 。 示例 1: 输入&am…...

HTTP和TCP代理原理及实现,主要是理解
Web 代理是一种存在于网络中间的实体,提供各式各样的功能。现代网络系统中,Web 代理无处不在。我之前有关 HTTP 的博文中,多次提到了代理对 HTTP 请求及响应的影响。今天这篇文章,我打算谈谈 HTTP 代理本身的一些原理,…...

MySQL中的连接池
数据库的连接池 1 )概述 网站连接数据库,为庞大用户的每次请求创建一个连接是不合适的关闭并重新连接的成本是很大的处理方法:设置最大值, 最小值, 设置最多闲置连接,设置等待阻塞 2 )示例演示 import threading i…...

css计时器 animation实现计时器延时器
css计时器 animation实现计时器延时器 缺点当切页面导航会休眠不执行 最初需求是一个列表每个项目都有各自的失效时间 然后就想到 计时器延时器轮询等方案 这些方案每一个都要有自己的计时器 感觉不是很好 轮询也占资源 然后突发奇想 css能不能实现 开始想到的是transition测…...
【win11 绕过TPM CPU硬件限制安装】
Qt编程指南 VX:hao541022348 ■ 下载iso文件■ 右键文件点击装载出现如下问题■ 绕过TPM CPU硬件限制安装方法■ 虚拟机安装win11 ■ 下载iso文件 选择Windows11 (multi-edition ISO)在选择中文 ■ 右键文件点击装载出现如下问题 ■ 绕过T…...
)
k8s的yaml文件中的kind类型都有哪些?(清单版本)
在操作kubernetes的过程中,我们接触到的yaml文件中的kind类型有很多。他们代表了kubernetes的不同类型的对象,了解了kind的类型,也就相当于了解了k8s都有哪些类型的对象。 类型清单及概要说明 序号类型简述1Pod一个Kubernetes中最基本的资源…...

Jetpack Room使用
Room使用 回顾 数据库有多张表,一张表只能记录一种Class,Class的具体属性是这个表的列;所有对表的操作都要通过Dao来访问 注解说明: Enity 作用于Class上,表示创建一张表记录该Class,Class内部属性使用…...
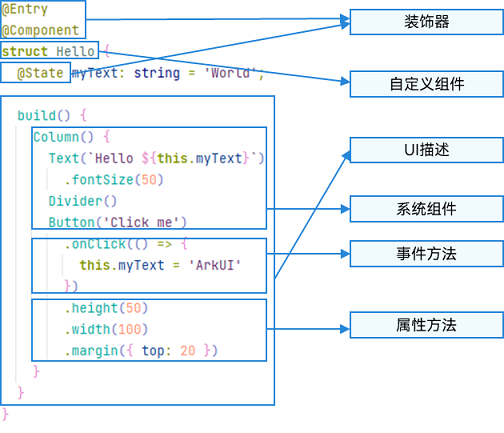
HarmonyOS应用开发之ArkTS语言学习记录
1、ArkTS介绍 ArkTS是鸿蒙生态的应用开发语言。它在保持TypeScript(简称TS)基本语法风格的基础上,对TS的动态类型特性施加更严格的约束,引入静态类型。同时,提供了声明式UI、状态管理等相应的能力,让开发者…...

windows 下 mongodb6.0 导入导出json文件
1.运行cmd窗口,进入MongoDB安装路径下的bin文件下,输入以下命令导入数据文件 mongoimport --host 127.0.0.1 --port 27017 --db <数据库名称,根据自个情况> -c <集合名称,自定义> --file <导入文件的路径名> …...

如何给 unplugin-vue-components/vite 写一个简单的 resolver
大部分工作 unplugin-vue-components 都已经处理好了, 我们只需要接收组件名来判断是否是自己的组件, 然后处理对应的导入逻辑。 一共 3 个字段 as 重命名类似 import { componentNameReName } from ‘xxxx’name 组件名 import { componentName } from ‘xxxx’from 导入路径…...
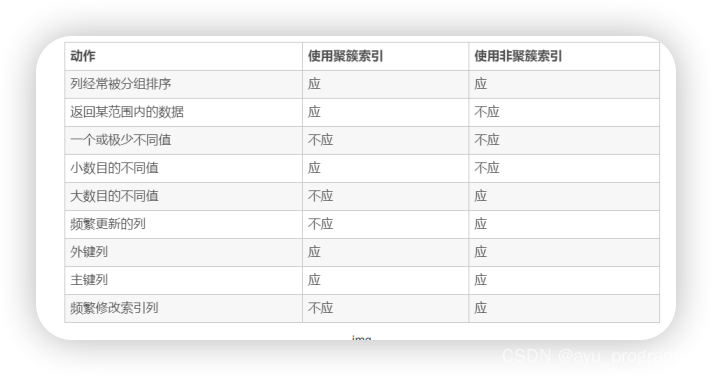
MYSQL篇--索引高频面试题
mysql索引 1什么是索引? 索引说白了就是一种数据结构,可以协助快速查询数据,以及更新数据库表中的数据,更通俗的来说索引其实就是目录,通过对数据建立索引形成目录,便于去查询数据,而mysql索引…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
