1.6PTA集练7-5~7-24、7-1、7-2,堆的操作,部落冲突(二分查找)
7-5 大師と仙人との奇遇 分数 20
#include<iostream>
#include<queue>
using namespace std;
int n;
long long ans=0,num;
priority_queue<long long,vector<long long>,greater<long long>>q;//记录之前买的,用小顶堆,最上面就是最小的
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>num;while(!q.empty()&&q.top()<num){ans+=(num-q.top());q.pop();}//先卖掉之前的if(i!=n)q.push(num);}while(!q.empty()){ans+=(num-q.top());q.pop();}cout<<ans;return 0;
}采用优先队列,每天,输入一个数,然后检测之前买的股票能不能在今天卖出去,即堆顶元素和今天的比较,不过记得比较之前要保证队列不空,今天卖完后就把今天的股票买进队列里,最后一天不买
然后最后的时候把所以股票都卖掉
7-6 插入排序 分数 10
#include<iostream>
using namespace std;
int n,arr[101];
int main(){cin>>n;for(int i=0;i<n;i++)cin>>arr[i];for(int i=1;i<n;i++){//表示要插入的元素int j=i-1,temp=arr[i];while(j>=0&&arr[j]>temp){arr[j+1]=arr[j];j--;}arr[j+1]=temp;for(int k=0;k<n;k++){cout<<arr[k];if(k!=n-1)cout<<" ";}if(i!=n-1)cout<<endl;}return 0;
}调整牌堆时,是和插入的新牌比较,如果比它大,就把这张牌往后移,即arr[j+1]=arr[j]
while终止时,j=-1越界,或者指向第一个比他小的元素,这张牌是不应该在这里的,所以就放在后面即j+1的位置上
7-7 冒泡排序 分数 15
#include<iostream>
using namespace std;
int n,arr[101];
void swap(int i,int j){int temp=arr[j];arr[j]=arr[i];arr[i]=temp;
}int main(){cin>>n;for(int i=0;i<n;i++)cin>>arr[i];for(int i=n-1;i>0;i--){//表示冒泡的天花板bool flag=false;//每次都建立一个标志,标志是否从发生了交换,如果没有的话就说明已经排序完成for(int j=0;j<i;j++){//表示冒泡的起点,每次都是从最底端开始冒泡if(arr[j]>arr[j+1]){swap(j,j+1);flag=1;//发生了排序交换}}if(flag){for(int k=0;k<n;k++){cout<<arr[k];if(k!=n-1)cout<<" ";}//只有发生了改变才打印if(i!=1)cout<<endl;}else{break;//没有的话就直接退出}}return 0;
}冒泡排序的话,每次确定一个天花板,因为在冒泡的过程中,是最大的元素不断到最大的位置上,所以最大的位置就不用再逐一判断了
然后冒泡都是从最底端开始冒泡,遍历到此时的天花板上,由于这一特性,冒泡排序将会使每次循环都会交换元素,如果一旦有一次没交换元素,那就说明排序已经终止
这一点在插入排序中不适用
7-8 小球装箱游戏 分数 200
每个球箱的数量一样多,是严格的限制
那就是先排序,然后加入
#include<iostream>
#include<algorithm>
using namespace std;
int n,br=0,bg=0,tr=0,tg=0;
struct node{int num,type;
}arr[100005];
bool cmp(node a,node b){if(a.num!=b.num){return a.num<b.num;}else{return a.type>b.type;}
}
int main(){cin>>n;//for(int i=1;i<=n;i++){cin>>arr[i].num>>arr[i].type;if(arr[i].type){tg++;}else{tr++;}}sort(arr+1,arr+n+1,cmp);for(int i=1;i<=n/2;i++){if(arr[i].type){bg++;}else{br++;}}cout<<tr-br<<" "<<tg-bg<<endl;cout<<br<<" "<<bg;return 0;
}7-9 二路归并排序 分数 10
在归并中,先判断是不是为空(不存在),然后是不是递归底层(这里是不做处理,因为只有一个元素),接着就是做递归处理,处理完后进行操作,这个操作就是进行合并,即所谓分治法,向下递归是分,然后“治”,合并。
求叶子结点数量以及树的高度也都是分治的思路
处理到文件尾,就是在while里cin>>n
#include<iostream>
using namespace std;
int n,arr[101];
void merge(int begin,int end){if(begin>=end)return;int i=begin,j=begin,mid=(begin+end)>>1,k=mid+1;int temp[101];merge(begin,mid);merge(k,end);while(j<=mid&&k<=end){if(arr[j]<=arr[k]){temp[i++]=arr[j++];}else{temp[i++]=arr[k++];}}while(j<=mid){temp[i++]=arr[j++];}while(k<=end){temp[i++]=arr[k++];}for(int i=begin;i<=end;i++)arr[i]=temp[i];for(int i=0;i<n;i++){cout<<arr[i];if(i!=n-1)cout<<" ";}if(begin!=0||end!=n-1)cout<<endl;
}
int main(){while(cin>>n){for(int i=0;i<n;i++)cin>>arr[i];merge(0,n-1);cout<<endl;}return 0;
}还需要注意的是,递归过程的打印,递归处理是栈的过程,即先到后出,
即最上层的是最后打印的,所谓最后打印就是最后才会结束所有本层的递归语句,即最后是打印
检测是不是最上层,就是检测左右区间,只有左右都是端点,才是最上层,不然的话就分行
7-10 成绩排名 分数 50
注意sort函数是左闭右开的,即处理左边的元素(是处理的第一个元素),不处理右边的元素(是不处理的第一个元素)
#include<iostream>
#include<algorithm>
using namespace std;
int n;
struct node{int ch,math,id;
}arr[100005];
bool cmp(node a,node b){if(a.ch!=b.ch){return a.ch>b.ch;}else if(a.math!=b.math){return a.math>b.math;}else{return a.id<b.id;}
}
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>arr[i].id>>arr[i].ch>>arr[i].math;}sort(arr+1,arr+n+1,cmp);for(int i=1;i<=n;i++)cout<<arr[i].id<<endl;return 0;
}7-11 根据后序序列和中序序列确定二叉树 分数 10
一种写法是递归函数参数是子树大小以及起点,另一种是参数是起点与终点
下面是起点与终点,有问题版
#include<iostream>
using namespace std;
int n,post[12],in[12];
struct node{int val;node*lchild,*rchild;node(int x):val(x),lchild(nullptr),rchild(nullptr){}
};
node* func(int pend,int pbegin,int iend,int ibegin){if(iend<ibegin)return nullptr;if(iend==ibegin){node* root=new node(in[iend]);return root;}int rindex;//根节点在中序的位置,同时也是左子树大小for(rindex=ibegin;rindex<=iend;rindex++){if(in[rindex]==post[pend]){break;}}node* root=new node(post[pend]);root->lchild=func(pbegin+rindex-1,pbegin,rindex-1,ibegin);root->rchild=func(pend-1,pbegin+rindex,iend,rindex+1);return root;
}
int h(node*root){if(!root)return 0;if(!root->lchild&&!root->rchild)return 1;return max(h(root->lchild),h(root->rchild))+1;
}
void pre(node*root){if(!root)return;cout<<root->val<<" ";pre(root->lchild);pre(root->rchild);
}
int main(){while(cin>>n){for(int i=1;i<=n;i++)cin>>post[i];for(int i=1;i<=n;i++)cin>>in[i];node*root=func(n,1,n,1);cout<<h(root)<<" ";pre(root);cout<<endl;}return 0;
}下面这个是没问题的,问题出在了,直接认为根节点在中序中的位置就是此时左子树的大小,实际上并不是,只有当此时中序起点为0时,这个下标才是此时左子树的大小,不然左子树大小就是根节点下标减去中序起点
#include<iostream>
using namespace std;
int n,post[12],in[12];
struct node{int val;node*lchild,*rchild;node(int x):val(x),lchild(nullptr),rchild(nullptr){}
};
node* func(int pend,int pbegin,int iend,int ibegin){if(iend<ibegin)return nullptr;if(iend==ibegin){node* root=new node(in[iend]);return root;}int rindex;//根节点在中序的位置for(rindex=ibegin;rindex<=iend;rindex++){if(in[rindex]==post[pend]){break;}}node* root=new node(post[pend]);int lsize=rindex-ibegin;root->lchild=func(pbegin+lsize-1,pbegin,rindex-1,ibegin);root->rchild=func(pend-1,pbegin+lsize,iend,rindex+1);return root;
}
int h(node*root){if(!root)return 0;if(!root->lchild&&!root->rchild)return 1;return max(h(root->lchild),h(root->rchild))+1;
}
void pre(node*root){if(!root)return;cout<<" "<<root->val;pre(root->lchild);pre(root->rchild);
}
int main(){while(cin>>n){for(int i=1;i<=n;i++)cin>>post[i];for(int i=1;i<=n;i++)cin>>in[i];node*root=func(n,1,n,1);cout<<h(root);pre(root);cout<<endl;}return 0;
}在递归中,依然是先判断空,然后判断递归底层,再就是递归处理部分
减法的理解
还有就是减法的细节,给定区间端点i,j的话,j-i是j和i之间的差距,可以看成j和i之间棍子的数量
另一种看法是i和j之间的端点数量,是只包含1个端点以及中间所有端点的数量
j-i+1是包含两个区间端点的
在这里,求左子树的大小,左端点是序列起点,右端点是根节点位置,显然左端点在左子树里,右端点不在左子树里,所以减法是左子树大小=根节点位置-序列起点,即只包含区间的一个端点的元素数量,即把根节点排除在外的区间元素数量,即左子树大小
然后是要去确定左右子树的后序中序的起点与终点,就是依据子树大小来确定判断,+1-1的细节靠子树大小去试
这里需要注意,递归参数是左右都闭的,也就是说左右是严格包含的,意思就是说这个划定好的端点结点是严格处于左右子树里的(依据左子树大小去判断具体下标),
此时通过左子树大小判断时,就要采用右端点-左端点+1,因为是严格包含在子树里的,所以左右端点都被包含![]()
上面的求法,思路是通过后序起点,然后利用左子树大小,使出来是这个数,
或者由上面减法的理解,左子树的大小也可以是左端点到根节点之间棍子的数量,而如果要定位到根节点的前一个结点,就只需要减少一个棍子,也就是p+l-1就代表右端点,p+l代表根节点位置,是第一个不在左子树里的元素的位置
即求size的大小是减法的元素数量只含一个端点的理解,求具体的下标是棍子间隔的理解
最后注意输出格式,如果不要每行末尾的空格,空格就改成这样输出
即先输出空格再输出元素就行
7-12 哈夫曼树 分数 25
相比于直接构造哈夫曼树以及获得哈夫曼编码还是弱了一点
#include<iostream>
#include<queue>
using namespace std;
priority_queue<int,vector<int>,greater<int>>q;
int n,num,ans=0;
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>num;q.push(num);}while(q.size()>1){int num1=q.top();q.pop();int num2=q.top();q.pop();ans+=(num1+num2);q.push(num1+num2);}cout<<ans;return 0;
}思路还是优先队列,通过优先队列来完成有规则的递归,在处理过程中就进行了每步的ans+=,完成了对ans的修改,即同一份数据会在处理过程中不断的被加,如果够小的话,而不用建完树后再对它进行处理去求路径长度
7-13 堆的操作 分数 20
#include<iostream>
using namespace std;
int n,k,arr[1005],cnt=0,id,num,m;
void swap(int i,int j){int temp=arr[j];arr[j]=arr[i];arr[i]=temp;
}
void up(int index){int par=index/2;while(par>=1){if(arr[par]>arr[index]){swap(par,index);index=par;par=index/2;}else{break;}}
}
void down(int index){int lc=2*index;while(lc<=cnt){if(lc+1<=cnt){lc=arr[lc]<arr[lc+1]?lc:lc+1;}if(arr[index]>arr[lc]){swap(index,lc);index=lc;lc=index*2;}else{break;}}
}
void insert(int x){if(cnt>=n)return;arr[++cnt]=x;up(cnt);
}
void del(){swap(1,cnt--);down(1);
}
int main(){cin>>n>>k;for(int i=1;i<=k;i++){cin>>id;if(id==1){cin>>num;insert(num);}else{del();}for(int j=1;j<=cnt;j++){cout<<arr[j];if(j!= cnt)cout<<" ";}cout<<endl;}cin>>m;for(int i=1;i<=m;i++)cin>>arr[i];cnt=m;for(int i=m/2;i>=1;i--){down(i);}for(int i=1;i<=m;i++){cout<<arr[i];if(i!=m)cout<<" ";}return 0;
}上调操作

就是从当前的位置往上找,下标从1开始的话,父母结点就是index/2;
然后操作终止的条件就是没有父母结点,即往上就没有了,即par>=1,只要还有父母结点,就还可能继续操作;然后能够继续上调的标志就是父母比自己大(因为要小顶堆),那就交换,然后更新孩子与父母,继续向上调整,直到不能,或者 没有父母,自己就已经是最小的
下调操作

下调的话可能有两个路径,选那个最小的路径换上来,
能够继续操作的前提是存在孩子结点,首先左孩子是最小的,所以迭代是要让左孩子不越界,接着判断是否存在右孩子,如果存在的话判断出一个最小的,然后尝试与此时的父结点交换,如果能换的话,说明可以继续向下,更新父节点与孩子结点,不然就说明最小的孩子都比此时的父节点大,那么已经满足堆的要求了,就不用再调整了
插入与删除

在插入的时候有细节就是如果此时堆已经满了的话,就不继续插入,直接返回了,所以需要加一个判断是cnt>=n
如果可以继续插入,就在新位置上放入元素,然后尝试把这个元素往上调整即可
对于删除,是取出堆顶元素,然后就是要让最后的元素放在堆顶上,然后把这个元素往下调整即可
在插入删除时,都要记得对cnt进行相应的操作
然后是第二部分,快速建堆,此时输入m后记得要更新堆的大小为m,不更新的话保留的依然是上个堆的大小
朴素建堆就是插入一个就上移调整一个,快速建堆是先都放好,放好后再从最后一个非叶子结点开始调整,进行向下调整,往回往上走,这样的话到上面时,下面的都已经满足了堆的要求
即朴素建堆主要用上调,快速建堆主要用向下调整
7-14 堆的建立 分数 20
说的是调整已经存在的N个元素,所以采用快速建堆
#include<iostream>
using namespace std;
int n,arrmin[10005],arrmax[10005];
void swap(int&i,int&j){int temp=i;i=j;j=temp;
}
void downmin(int index){int c=index*2;while(c<=n){if(c+1<=n){c=arrmin[c]<arrmin[c+1]?c:c+1;}if(arrmin[index]>arrmin[c]){swap(arrmin[index],arrmin[c]);index=c;c=index*2;}else{break;}}
}
void downmax(int index){int c=index*2;while(c<=n){if(c+1<=n){c=arrmax[c]>arrmax[c+1]?c:c+1;}if(arrmax[index]<arrmax[c]){swap(arrmax[index],arrmax[c]);index=c;c=index*2;}else{break;}}
}
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>arrmin[i];arrmax[i]=arrmin[i];}for(int i=n/2;i>=1;i--){downmin(i);downmax(i);}for(int i=1;i<=n;i++){cout<<arrmax[i];if(i!=n)cout<<" ";}cout<<endl;for(int i=1;i<=n;i++){cout<<arrmin[i];if(i!=n)cout<<" ";}return 0;
}7-15 折半(二分)查找 分数 20
#include<iostream>
#include<algorithm>
using namespace std;
int n,arr[100005],tar,l,r;
int search(int tar,int l,int r){if(l>r)return -1;int left=l,right=r,mid=(left+right)>>1;while(left<=right){//只要区间里还有元素就可以继续操作if(arr[mid]==tar){return mid;}else if(arr[mid]<tar){left=mid+1;}else{right=mid-1;}mid=(left+right)>>1;}return -1;
}
int main(){cin>>n;for(int i=0;i<n;i++){cin>>arr[i];}sort(arr,arr+n);cin>>n;for(int i=1;i<=n;i++){cin>>tar>>l>>r;cout<<search(tar,l,r)<<endl;}return 0;
}这个查找,先判断是不是空,即l>r,
然后在迭代中,判断能否继续操作,操作的前题是区间里还有元素,即left<=right,然后就是找
如果刚好就返回,小于目标值就往右找,大于目标值就往左找,
后面两种情况由于已经判断过了中间端点,所以在下一轮查找中直接舍弃掉,即查找的过程包含两个区间端点,
7-16 部落冲突 分数 40
去求每个坐标位置对应的左边的面积,然后去找一个与总面积的一半最接近的位置,而且还要满足左边的大于总的减去左边的,即左边和总的一半的差值必须不是负的,必须是0或者正
要求
#include<iostream>
#include<queue>
using namespace std;
struct node{int begin,end,h;
}arr[105];
struct cmp{bool operator()(node a,node b){return a.begin>b.begin;}
}
priority_queue<node,vector<node>,cmp>q;
int n,x,y,w,h,tot=0,maxx=0,minx=1e8;
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>x>>y>>w>>h;arr[i].begin=x;//也就是说绿洲的终止点是在x+w,100处arr[i].end=x+w;//端点数量是w+1,但是长度是w,就是连接的棍子数量arr[i].h=h;maxx=max(maxx,arr[i].end);tot+=w*h;q.push(arr[i]);}for(int i=arr[i].begin;i<=maxx;i++){int cnt=0;while(q.top()<i){}}return 0;
}先按起点从小到大排,然后遍历每个绿洲,如果加上这个绿洲面积不比一般大,那就直接加,并直接下一个
上面的思路是类似于前缀和的,但是由于在输入的时候,左端点与右端点都不知道,所以就很难搞,
可解决
这里就是直接不预处理了,直接二分,在二分的过程中去计算
每次计算都遍历所有的部落,
时间复杂度应该是nlogm的一个级别
上面前缀和的话,每次输入就处理,处理的复杂度是nm差不多,再二分查找,是logm
好像还是在二分过程中去计算会好一点
这个之所以能直接二分,就是是左边累加,一直往右,就是左边面积是递增的,即使不处理也是这样,所以干脆就先不处理了,省去了处理的时间,而是只关注需要的,想要的点的信息,需要的时候就通过Get来计算得到
#include <iostream>
#include <vector>
#include <algorithm>
#include<stack>
#include<queue>
#include <unordered_set>
using namespace std;
#define ll long long
const int N = 105;
struct node {int l, r, w, h;
}s[N];
int n;
ll getd(int mid) {ll sl = 0, sr = 0;for (int i = 1; i <= n; i++) {if (s[i].r <= mid) {sl += (ll)s[i].w * s[i].h;}else if (s[i].l >= mid) {sr += (ll)s[i].w * s[i].h;}else {sl += (ll)s[i].h * (mid - s[i].l);sr += (ll)s[i].h * (s[i].r - mid);}}return sl - sr;
}
//就是说,地图上有很多块,然后划一条线,使这条线上所有左侧的块都归属于A
//剩下的都给B,然后要让A>>B
//自左到右,累积的岛屿面积是不断增加的
//也就是说每个x坐标轴都对应一个值,这个值就是自左到右的岛屿面积,类似于分布函数int main() {cin >> n;int R = 0, L = 1000;for (int i = 1; i <= n; i++) {int x, y, w, h;cin >> x >> y >> w >> h;s[i].l = x, s[i].r = x + w, s[i].w = w, s[i].h = h;R = max(R, s[i].r);L = min(L, s[i].l);}int ans = -1;ll da = 1e10;while (L <= R) {int mid = (L + R) >> 1;ll t = getd(mid);if (t < 0) {L = mid + 1;}else {da = min(da, t);R = mid - 1;ans = mid;}}// while (ans < R && getd(ans + 1) == da) {// ans++;//}cout << ans;return 0;
}#include<iostream>
#include<queue>
#include<algorithm>
using namespace std;
int n,x,y,w,h,l=1e8,r=0,ans;
struct node{int begin,end,h;long long s;
}arr[105];
long long tot=0;
long long gets(int index){long long sl=0;for(int i=1;i<=n;i++){if(arr[i].end<=index){sl+=arr[i].s;}else if(arr[i].begin<index){sl+=(long long)(index-arr[i].begin)*h;}}return sl*2-tot;
}
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>x>>y>>w>>h;arr[i].begin=x,arr[i].end=x+w,arr[i].h=h,arr[i].s=w*h;l=min(l,x),r=max(r,x+w);tot+=arr[i].s;}while(l<=r){int mid=(l+r)>>1;long long ds=gets(mid);if(ds<0){l=mid+1;}else{r=mid-1;ans=mid;}}cout<<ans;return 0;
}#include<iostream>
#include<queue>
#include<algorithm>
using namespace std;
int n,x,y,w,h,l=1e8,r=0,ans;
struct node{int begin,end,h;long long s;
}arr[105];
long long gets(int index){long long sl=0,sr=0;for(int i=1;i<=n;i++){if(arr[i].end<=index){sl+=arr[i].s;}else if(arr[i].begin>=index){sr+=arr[i].s;}else{sl+=(long long)(index-arr[i].begin)*arr[i].h;sr+=(long long)(arr[i].end-index)*arr[i].h;}}return sl-sr;
}
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>x>>y>>w>>h;arr[i].begin=x,arr[i].end=x+w,arr[i].h=h,arr[i].s=(long long)w*h;l=min(l,x),r=max(r,x+w);}while(l<=r){int mid=(l+r)>>1;long long ds=gets(mid);if(ds<0){l=mid+1;}else{r=mid-1;ans=mid;}}cout<<ans;return 0;
}经过排查发现,问题就出现在数据范围上,就是Longlong ,
首先一定要开long long, 然后涉及Longlong的数据类型,如果是从Int型转过来的,也一定要开Longlong
还有就是longlong*2容易直接爆掉,所以还得是缓行,不能随便的乘,容易爆
这也是(left+right)>>1和left+(right-left)>>1等价,但是保险写后面的原因,因为写前面的话,如果数据比较大,就会爆掉出错
总之,这题的思路就是记录范围的左边与右边,然后开始二分查找,使面积差最小,小于0是不能接收的,大于0的话,就尝试继续找,只要还能继续找,就有可能继续缩小这个差距,从而找到最小的面积差
7-17 判断是否二叉排序树 分数 10
#include<iostream>
#include<string>
using namespace std;string s;int index=0;
struct node{int val;node*lchild,*rchild;node(int x):val(x),lchild(nullptr),rchild(nullptr){}
};
node* cr(){if(index>=s.size())return nullptr;if(s[index]=='*')return nullptr;node* root=new node(s[index++]-'0');root->lchild=cr();root->rchild=cr();return root;
}
bool isbst(node*root){if(!root)return true;if(!root->rchild&&!root->lchild)return true;if(root->rchild&&root->val>root->rchild->val)return false;if(root->lchild&&root->val<root->lchild->val)return false;return isbst(root->rchild)&&isbst(root->lchild);
}
int main(){node*root;while(cin>>s){index=0;node*root=cr();if(isbst(root))cout<<"YES"<<endl;else cout<<"NO"<<endl;}return 0;
}主要是建树的细节 以及处理到文件尾的操作
采用输入string,然后对string做处理从而完成建树
这里需要注意,index表示跟踪现在这个字符串建树建到哪了,每建一个结点,index就往后移一位,表示此时的结点已经被建立了,由于给的是先序的字符串,所以是先建,再递归左右,
递归依旧是,判断是否为空,然后是否为底层,是否满足条件,然后递归处理,本层处理
在每次时,都要把index游标重新置0
至于BST的判断逻辑,就是是否为空,是否为底层,
再就是每层的判断以及向下递归的部分
每层判断,如果有右孩子且比它大就是错的;有左孩子比他小就是错的,其它都是正确的,就递归向下,保证子树也都是BST即可
7-18 整型关键字的散列映射 分数 25
#include<iostream>
using namespace std;
int n,p,arr[11000],num;
int main(){cin>>n>>p;for(int i=1;i<=n;i++){cin>>num;int index=num%p;if(!arr[index]){arr[index]=num;cout<<index;}else{while(arr[index]&&arr[index]!=num){index=(index+1)%p;}arr[index]=num;cout<<index;}if(i!=n)cout<<" ";}return 0;
}就是先计算一下对应的下标,然后计算一下对应的哈希值,如果对应位置没有,就插入,不然的话就进行冲突处理,进行线性冲突处理,然后注意存储范围是模p,即0~p-1,所以就是需要注意一下处理后的坐标在这个范围内,所以index=(index+1)%p;
还有需要注意的一点是,要加入的元素可能有重复的,这也就是说哈希表里不能存重复相同的元素,而arr[index]只能够判断当前格子有没有被占用,不能判断是否和此时要插入的元素相同,所以就是要新增一个判断arr[index]!=num才行,如果不满足这个的话,也会退出循环
即这个while出来的时候,要么是第一个还没被占用的格子,要么是第一个已经存储过的相同元素
7-19 数据结构实验三 图的深度优先搜索 分数 50
#include<iostream>
using namespace std;
int n,m,u,v,g[25][25],cnt=0;
bool vis[25]={0};
void dfs(int u){cout<<u<<" ";for(int i=0;i<n;i++){if(vis[i])continue;if(g[u][i]){vis[i]=1;dfs(i);}}
}
int main(){cin>>n>>m;for(int i=1;i<=m;i++){cin>>u>>v;g[u][v]=g[v][u]=1;}for(int i=0;i<n;i++){if(!vis[i]){vis[i]=1;cnt++;dfs(i);}}cout<<endl<<cnt<<endl<<m;return 0;
}用bool类型的vis记录每个结点的访问情况,如果访问过就不继续访问,不然的话就dfs它,下一层在它的基础上进行访问,邻接矩阵可以保证是字典序的访问顺序
在外层,用cnt去记录联通分支数
7-20 抓住那头牛 分数 25
#include<iostream>
#include<queue>
using namespace std;
int n,k,t;
bool vis[100005]={0};
queue<pair<int,int>>q;
int main(){cin>>n>>k;vis[n]=1;q.push({n,0});while(!q.empty()){int cur=q.front().first;t=q.front().second;q.pop();if(cur==k)break;if(cur*2<=100000&&!vis[cur*2]){q.push({cur*2,t+1});vis[cur*2]=1;}if(cur-1>=0&&!vis[cur-1]){q.push({cur-1,t+1});vis[cur-1]=1;}if(cur+1<=100000&&!vis[cur+1]){q.push({cur+1,t+1});vis[cur+1]=1;}}cout<<t;return 0;
}为了防止未访问的结点在同一层(上层)中处理后会发生重复入队的情况,所以就是在入队的时候就对vis做操作,而不是在出队处理时再更改vis操作,这样可以保证在上层有多个结点可到达下层同一结点时,会只入队一个结点,从而减少了时间的复杂度
另外就是注意入队时,对下标的控制,即在合法范围内,不会出界,在遍历的时候,即只有下个位置的坐标处于0和1E5之间才会被考虑,否则不入队,直到遍历BFS搜索到目标点
7-21 任务拓扑排序 分数 10
这里就是注意要是字典序
直接层序不行,用邻接矩阵也不行,因为在上层当中,如果有大编号结点的入度比较小,先被减为0了,同时存在小编号结点,同样在上层,但是是后续被减为0的,那么在下一层当中,就会优先去访问那个大编号结点,而不是小编号结点,从而打破了字典序
即建立在层序上的,不能保证为字典序
所以应该是要用优先队列,以小顶堆,编号最小建堆,这样无论是第几层解锁到的结点,都会被优先访问从而保证字典序
#include<iostream>
#include<queue>
using namespace std;
int n,e,in[105],g[105][105],u,v,ans[105],cnt=0;
priority_queue<int,vector<int>,greater<int>>q;
bool vis[105]={0};
int main(){cin>>n>>e;for(int i=0;i<n;i++)in[i]=0;for(int i=1;i<=e;i++){cin>>u>>v;g[u][v]=1;in[v]++;}for(int i=0;i<n;i++){if(!in[i]){q.push(i);vis[i]=1;}}while(!q.empty()){int cur=q.top();ans[++cnt]=cur;q.pop();for(int i=0;i<n;i++){if(g[cur][i]&&!vis[i]){in[i]--;if(!in[i]){vis[i]=1;q.push(i);}}}}if(cnt==n){for(int i=1;i<=n;i++)cout<<ans[i]<<" ";}else{cout<<"unworkable project";}return 0;
}7-22 信使 分数 100
堆优化
#include<iostream>
#include<queue>
using namespace std;
typedef pair<int,int> pii;
priority_queue<pii,vector<pii>,greater<pii>>q;
int n,m,cnt=0,u,v,w,dis[105],ans=-1,head[105];
bool vis[105];
struct edge{int v,next,w;
}e[1000005];
void add(int u,int v,int w){e[++cnt].v=v;e[cnt].w=w;e[cnt].next=head[u];head[u]=cnt;
}
int main(){cin>>n>>m;for(int i=1;i<=n;i++)dis[i]=1e8;for(int i=1;i<=m;i++){cin>>u>>v>>w;add(u,v,w);add(v,u,w);}vis[1]=1;for(int i=head[1];i;i=e[i].next){dis[e[i].v]=e[i].w;q.push({e[i].w,e[i].v});}while(!q.empty()){int tar=q.top().second,d=q.top().first;q.pop();if(vis[tar])continue;vis[tar]=1;for(int i=head[tar];i;i=e[i].next){if(dis[e[i].v]>d+e[i].w){dis[e[i].v]=d+e[i].w;q.push({d+e[i].w,e[i].v});}}}for(int i=1;i<=n;i++){ans=max(ans,dis[i]);}if(ans>=1e8){cout<<-1;}else cout<<ans;return 0;
}
这部分是链式前向星,注意cnt是边的编号,head记录该起点的第一个边的编号,然后每个边记录下一条边的编号![]()
接着是堆的定义,这里定义数对,gretaer优先判断第一个数,然后相同时再判断编号
就是第一个是距离,第二个是编号,记得typedef后面要加;
还有就是边,边的结构体数组要开大点
初始入队,
入队不会确定结点,只有从优先队列中取出元素时才会确定被访问过,也就是说,当一个结点被访问过时,队列中可能还会存在这个元素,
注意注意,这里vis放的位置和之前那个有所不同,之前那个7-20,是严格的层序,因为是要最早遇到,所以就要避免同一层上,重复的访问到某些结点,所以在第一次遇到的时候,就要vis,因为已经确定到可以访问了,即入队时就Vis
而至于这个有优先顺序的,只有在出队时才会被确定真正访问到,这里就是出队时才vis,这也是拓扑排序要字典序时,在出队时vis,而不是入队时Vis,如果是任意的随便都行
dis始终保持为此时最小的距离
7-23 校园最短路径 分数 10
#include<iostream>
#include<queue>
#include<string>
using namespace std;
typedef pair<int,int> pii;
priority_queue<pii,vector<pii>,greater<pii>>q;
int n,m,w,cnt=0,head[100],pre[100],dis[100];
bool vis[100]={0};
string s,s2;
struct node{int v,w,next;
}e[10000];
void add(int u,int v,int w){e[++cnt].v=v;e[cnt].w=w;e[cnt].next=head[u];head[u]=cnt;
}
void path(int index){if(pre[index]==-1){cout<<s[index];return;}path(pre[index]);cout<<"->"<<s[index];
}
int main(){cin>>n>>m>>s;for(int i=0;i<n;i++)dis[i]=1e8;for(int i=1;i<=m;i++){cin>>s2>>w;add(s.find(s2[0]),s.find(s2[1]),w);add(s.find(s2[1]),s.find(s2[0]),w);}vis[0]=1,dis[0]=0,pre[0]=-1;for(int i=head[0];i;i=e[i].next){dis[e[i].v]=e[i].w;q.push({e[i].w,e[i].v});}while(!q.empty()){int tar=q.top().second;q.pop();if(vis[tar])continue;vis[tar]=1;for(int i=head[tar];i;i=e[i].next){if(dis[e[i].v]>dis[tar]+e[i].w){dis[e[i].v]=dis[tar]+e[i].w;q.push({dis[e[i].v],e[i].v});pre[e[i].v]=tar;}}}for(int i=0;i<n;i++){if(dis[i]>=1e8){cout<<"dist[A]["<<s[i]<<"]="<<256<<endl;cout<<s[i]<<endl;}else{cout<<"dist[A]["<<s[i]<<"]="<<dis[i]<<endl;path(i);cout<<endl;}}return 0;
}7-24 最小生成树-kruskal算法 分数 15
#include<iostream>
#include<algorithm>
using namespace std;
struct edge{int u,v,w;
}e[405];
int n,m,fa[25];
int find(int x){if(fa[x]==x){return x;}fa[x]=find(fa[x]);return fa[x];
}
bool cmp(edge a, edge b){return a.w<b.w;
}
int main(){cin>>n>>m;for(int i=1;i<=n;i++)fa[i]=i;for(int i=1;i<=m;i++){cin>>e[i].u>>e[i].v>>e[i].w;}sort(e+1,e+m+1,cmp);for(int i=1;i<=m;i++){if(find(e[i].u)==find(e[i].v))continue;fa[find(e[i].u)]=find(e[i].v);cout<<min(e[i].u,e[i].v)<<","<<max(e[i].u,e[i].v)<<","<<e[i].w<<endl;}return 0;
}用并查集,合并的时候注意是合并根节点,其它就没什么了
7-1 冰雹猜想。 分数 10
#include<iostream>
using namespace std;
int n,cnt=0;
int main(){cin>>n;while(n!=1){cout<<n<<" ";if(!(n%2)){n=n/2;}else{n=n*3+1;}cnt++;}cout<<1<<endl<<"count = "<<cnt+1;return 0;
}这个题目有点问题,变化的次数输出要注意多1次
7-2 输入正整数n,打印图形。 分数 10
#include<iostream>
using namespace std;
int n;
int main(){cin>>n;for(int i=1;i<=n-1;i++){for(int j=1;j<=n-i;j++){cout<<" ";}for(int j=1;j<=2*i-1;j++){cout<<"*";}for(int j=1;j<=n-i;j++){cout<<" ";}cout<<endl;}for(int i=1;i<=2*n-1;i++)cout<<"*";cout<<endl;for(int i=n-1;i>=1;i--){for(int j=1;j<=n-i;j++){cout<<" ";}for(int j=1;j<=2*i-1;j++){cout<<"*";}for(int j=1;j<=n-i;j++){cout<<" ";}cout<<endl;}return 0;
}相关文章:

1.6PTA集练7-5~7-24、7-1、7-2,堆的操作,部落冲突(二分查找)
7-5 大師と仙人との奇遇 分数 20 #include<iostream> #include<queue> using namespace std; int n; long long ans0,num; priority_queue<long long,vector<long long>,greater<long long>>q;//记录之前买的,用小顶堆,最上面就是最…...

uniapp向上拉加载,下拉刷新
目录 大佬1大佬2 大佬1 大佬地址:https://blog.csdn.net/wendy_qx/article/details/135077822 大佬2 大佬2:https://blog.csdn.net/chen__hui/article/details/122497140...

目标检测脚本之mmpose json转yolo txt格式
目标检测脚本之mmpose json转yolo txt格式 一、需求分析 在使用yolopose及yolov8-pose 网络进行人体姿态检测任务时,有时需要标注一些特定场景的中的人型目标数据,用来扩充训练集,提升自己训练模型的效果。因为单纯的人工标注耗时费力&…...
大数据技术在民生资金专项审计中的应用
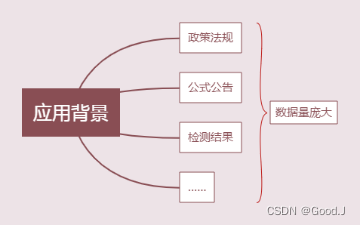
一、应用背景 目前,针对审计行业,关于大数据技术的相关研究与应用一般包括大数据智能采集数据技术、大数据智能分析技术、大数据可视化分析技术以及大数据多数据源综合分析技术。其中,大数据智能采集数据技术是通过网络爬虫或者WebService接口实现跨部门在线数据交互;大数…...

视觉SLAM十四讲|【四】误差Jacobian推导
视觉SLAM十四讲|【四】误差Jacobian推导 预积分误差递推公式 ω 1 2 ( ( ω b k n k g − b k g ) ( w b k 1 n k 1 g − b k 1 g ) ) \omega \frac{1}{2}((\omega_b^kn_k^g-b_k^g)(w_b^{k1}n_{k1}^g-b_{k1}^g)) ω21((ωbknkg−bkg)(wbk1nk1g−bk1g)) …...
「实战应用」如何用DHTMLX Gantt构建类似JIRA式的项目路线图(一)
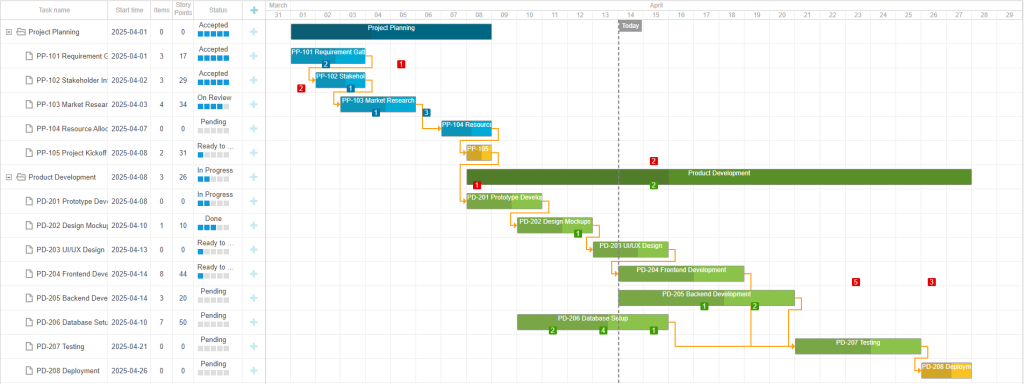
DHTMLX Gantt是用于跨浏览器和跨平台应用程序的功能齐全的Gantt图表。可满足项目管理应用程序的所有需求,是最完善的甘特图图表库。 在web项目中使用DHTMLX Gantt时,开发人员经常需要满足与UI外观相关的各种需求。因此他们必须确定JavaScript甘特图库的…...

【习题】应用程序框架
判断题 1. 一个应用只能有一个UIAbility。错误(False) 正确(True)错误(False) 2. 创建的Empty Ability模板工程,初始会生成一个UIAbility文件。正确(True) 正确(True)错误(False) 3. 每调用一次router.pushUrl()方法,页面路由栈数量均会加1。错误(Fal…...
java基于ssm的线上选课系统的设计与实现论文
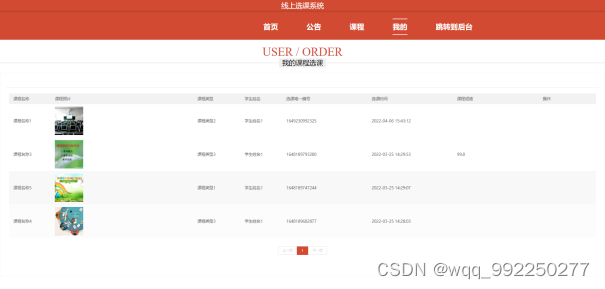
摘 要 在如今社会上,关于信息上面的处理,没有任何一个企业或者个人会忽视,如何让信息急速传递,并且归档储存查询,采用之前的纸张记录模式已经不符合当前使用要求了。所以,对学生选课信息管理的提升&#x…...
汽车雷达:实时SAR成像的实现
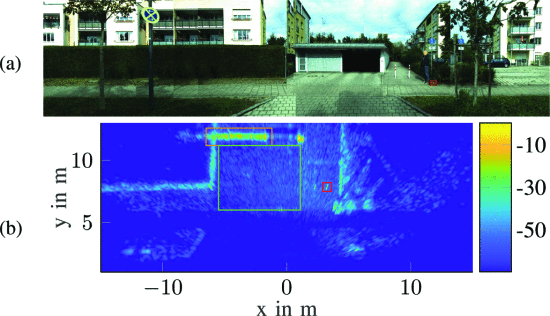
摘要: 众所周知,点云成像是目前实现汽车雷达感知最流行的方案,尤其是采用多级联实现的4D点云成像雷达,这是目前最有希望实现产品落地的技术方案之一。 今天重点分享关于汽车雷达SAR成像相关技术内容,这也证实了4D点云成像雷达并不一定就是汽车雷达成像唯一的方案,在业内…...
《C++语言程序设计(第5版)》(清华大学出版社,郑莉 董渊编著)习题——第2章 C++语言简单程序设计
2-15 编写一个程序,运行时提示输入一个数字,再把这个数字显示出来。 #include <iostream>using namespace std;int main() {// 提示用户输入数字cout << "请输入一个数字: ";// 用于存储用户输入的数字的变量double number;// 从…...

2023年生成式AI全球使用报告
生成式人工智能工具正在迅速改变多个领域,从营销和新闻到教育和艺术。 这些工具使用算法从大量培训材料中获取新的文本、音频或图像。虽然 ChatGPT 和 Midjourney 之类的工具可以用来实现超出人类能力或想象力的艺术效果,但目前它们最常用于比人类更轻松…...

安全防御之漏洞扫描技术
每年都有数以千计的网络安全漏洞被发现和公布,加上攻击者手段的不断变化,网络安全状况也在随着安全漏洞的增加变得日益严峻。寻根溯源,绝大多数用户缺乏一套完整、有效的漏洞管理工作流程,未能落实定期评估与漏洞修补工作。只有比…...
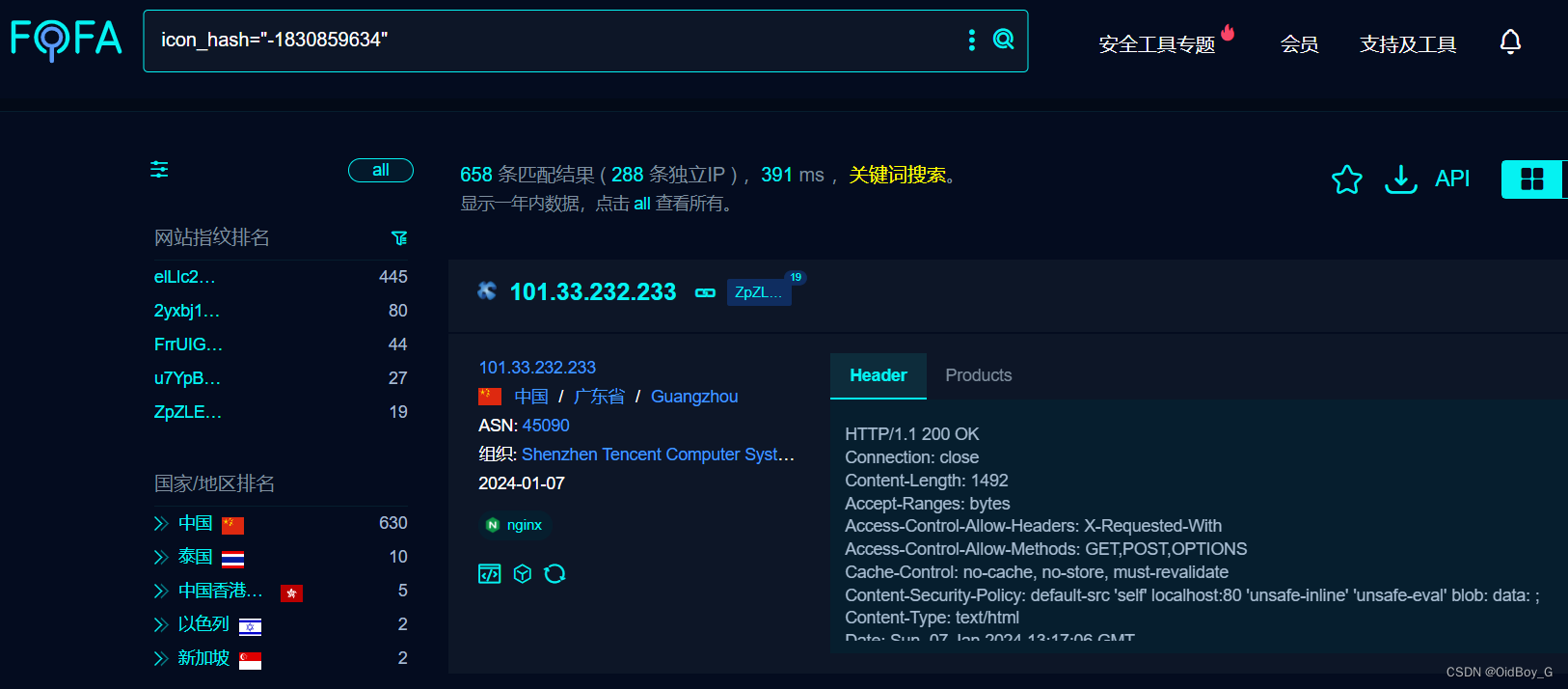
SPON世邦 IP网络对讲广播系统 多处文件上传漏洞复现
0x01 产品简介 SPON世邦IP网络对讲广播系统是一种先进的通信解决方案,旨在提供高效的网络对讲和广播功能。 0x02 漏洞概述 SPON世邦IP网络对讲广播系统 addscenedata.php、uploadjson.php、my_parser.php等接口处存在任意文件上传漏洞,未经身份验证的攻击者可利用此漏洞上…...
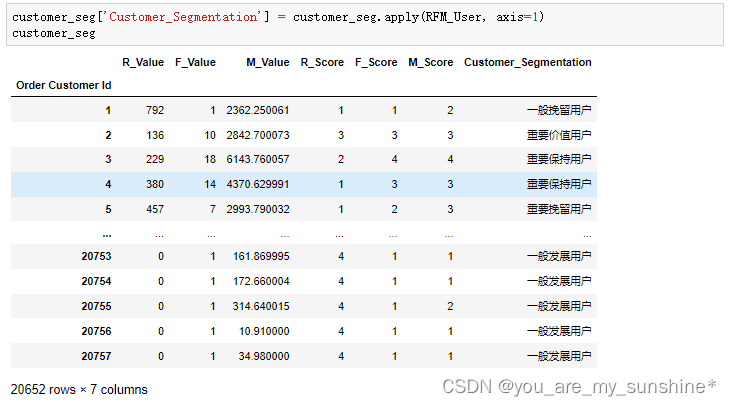
Python综合数据分析_RFM用户分层模型
文章目录 1.数据加载2.查看数据情况3.数据合并及填充4.查看特征字段之间相关性5.聚合操作6.时间维度上看销售额7.计算用户RFM8.数据保存存储(1).to_csv(1).to_pickle 1.数据加载 import pandas as pd dataset pd.read_csv(SupplyChain.csv, encodingunicode_escape) dataset2…...
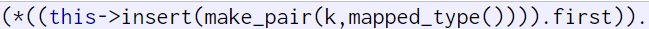
【C++进阶04】STL中map、set、multimap、multiset的介绍及使用
一、关联式容器 vector/list/deque… 这些容器统称为序列式容器 因为其底层为线性序列的数据结构 里面存储的是元素本身 map/set… 这些容器统称为关联式容器 关联式容器也是用来存储数据的 与序列式容器不同的是 其里面存储的是<key, value>结构的键值对 在数据检索时…...

在 Linux 中开启 Flask 项目持续运行
在 Linux 中开启 Flask 项目持续运行 在部署 Flask 项目时,情况往往并不是那么理想。默认情况下,关闭 SSH 终端后,Flask 服务就停止了。这时,您需要找到一种方法在 Linux 服务器上实现持续运行 Flask 项目,并在服务器…...

考研个人经验总结【心理向】
客官你好 首先,不管你是以何种原因来到这篇博客,以下内容或多或少可能带给你一些启发。如果你还是大二or大三学生,有考研的打算,不妨提前了解一些考研必备的心理战术,有时候并不是你知识学得不好,而是思维…...
如何在CentOS安装SQL Server数据库并通过内网穿透工具实现公网访问
文章目录 前言1. 安装sql server2. 局域网测试连接3. 安装cpolar内网穿透4. 将sqlserver映射到公网5. 公网远程连接6.固定连接公网地址7.使用固定公网地址连接 前言 简单几步实现在Linux centos环境下安装部署sql server数据库,并结合cpolar内网穿透工具࿰…...

jupyter内核错误
1、在dos窗口输入以下命令激活环境:anaconda activate 【py环境名,比如py37】(目的是新家你一个虚拟环境) 2、在虚拟环境py37下安装jupyter notebook,命令:pip install jupyter notebook 3、安装ipykerne…...
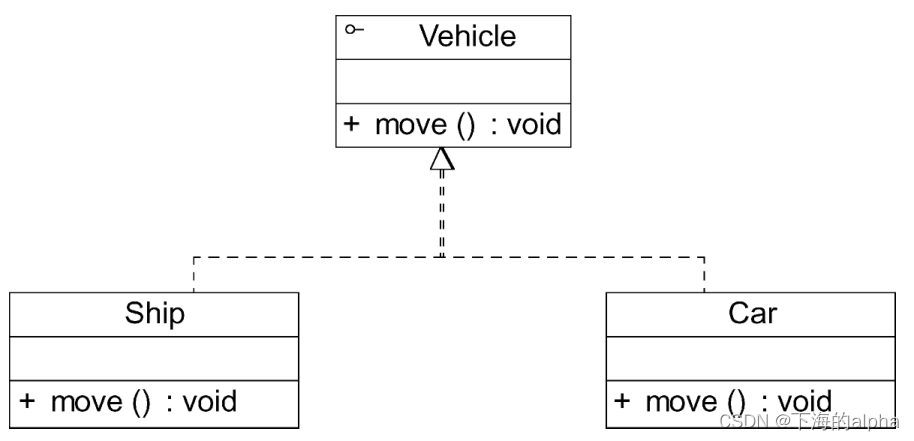
设计模式的艺术P1基础—2.3 类之间的关系
设计模式的艺术P1基础—2.3 类之间的关系 在软件系统中,类并不是孤立存在的,类与类之间存在各种关系。对于不同类型的关系,UML提供了不同的表示方式 1.关联关系 关联(Association)关系是类与类之间最常用…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...
