EM@三角函数诱导公式
文章目录
- 诱导公式
- 单位圆坐标和三角函数
- 记忆口诀
- 符号看象限
- 奇变偶不变
- 例
- 常用诱导公式🎈
- 常用部分(5对)
- 倒数关系
- 六种三角函数间的转换关系
- 小结
- Reflections
- Shifts and periodicity
诱导公式
- 诱导公式 - 维基百科,自由的百科全书 (wikipedia.org)
单位圆坐标和三角函数
-
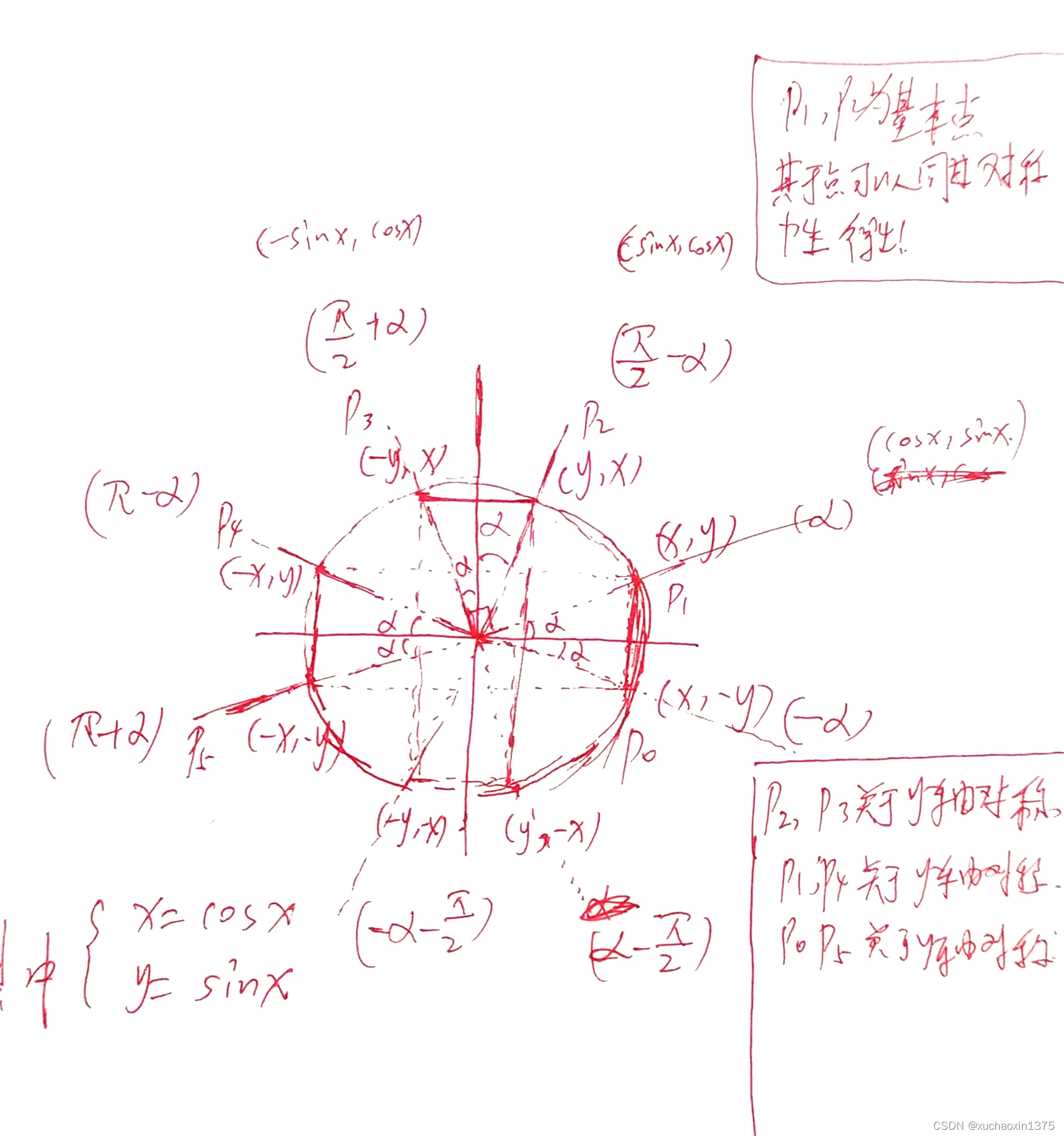
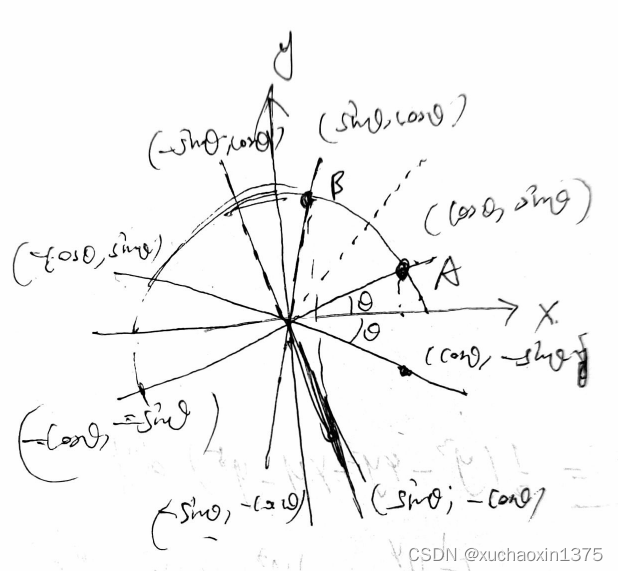

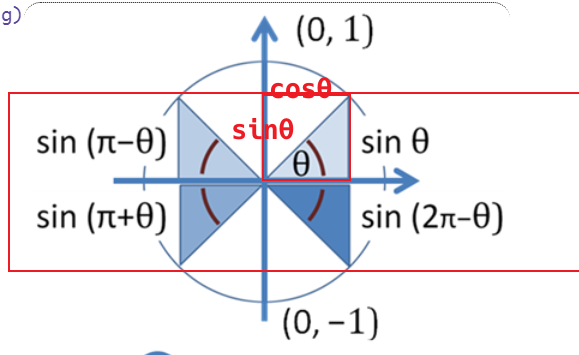
-
例如,sin(θ+π)=−sin(θ);这里ϕ(θ)=π+θsin(\theta+\pi)=- sin(\theta);这里\phi(\theta)=\pi+\thetasin(θ+π)=−sin(θ);这里ϕ(θ)=π+θ
-
途中各个点的横纵坐标分值分别对应p(cox(ϕ(θ)),sin(ϕ(θ)))途中各个点的横纵坐标分值分别对应p(cox(\phi(\theta)),sin(\phi(\theta)))途中各个点的横纵坐标分值分别对应p(cox(ϕ(θ)),sin(ϕ(θ)))
-
途中设定了两个超级点(主超级点为A(cosθ,sinθ),副超级点B(sinθ,cosθ)A(cos\theta,sin\theta),副超级点B(sin\theta,cos\theta)A(cosθ,sinθ),副超级点B(sinθ,cosθ)
- 所有的其他角度都可以由超级点关于x轴或者y轴或者圆心原点(或者θ=π2)对称所有的其他角度都可以由超级点关于x轴或者y轴或者圆心原点(或者\theta=\frac{\pi}{2})对称所有的其他角度都可以由超级点关于x轴或者y轴或者圆心原点(或者θ=2π)对称
- 比如ϕ(θ)=θ−π2;则sin(ϕ(θ))=−cosθ;cos(ϕ(θ))=sinθ\phi(\theta)=\theta-\frac{\pi}{2};则sin(\phi(\theta))=-cos\theta;cos(\phi(\theta))=sin\thetaϕ(θ)=θ−2π;则sin(ϕ(θ))=−cosθ;cos(ϕ(θ))=sinθ
记忆口诀
- 对于kπ2±α(k∈Z)k\frac{\pi}{2}\pm\alpha(k\in \mathbb{Z})k2π±α(k∈Z)的三角函数值,
符号看象限
- 口诀总是把α\alphaα看作锐角,2π−α∈(270°,360°),弧度角2π−α终边落在第4象限,sin(2π−α)<02π-α∈(270°,360°),弧度角2\pi-\alpha终边落在第4象限,sin(2π-α)<02π−α∈(270°,360°),弧度角2π−α终边落在第4象限,sin(2π−α)<0,符号为“-”
奇变偶不变
-
当k是偶数时,得到α的同名函数值,即函数名不改变;
-
当k是奇数时,得到α相应的余函数值,即
- sin→cos;cos→sin;tan→cot,cot→tan
-
然后在前面加上把α看成锐角时原函数值的符号
-
对于tan,sec,csc,cot\tan,\sec,\csc,\cottan,sec,csc,cot可以转化为cos,sin\cos,\sincos,sin处理
例
- sin(2π−α)=sin(4⋅π2−α)sin(2π-α)=sin(4·\frac{\pi}{2}-α)sin(2π−α)=sin(4⋅2π−α),k=4为偶数,所以函数名(绝对值部分)是sinα\sin\alphasinα。
- 所以sin(2π−α)=−sinαsin(2π-α)=-sinαsin(2π−α)=−sinα
常用诱导公式🎈
常用部分(5对)
-
sin(−α)=−sinα\sin(-\alpha)=-\sin{\alpha}sin(−α)=−sinα
-
cos(−α)=cosα\cos(-\alpha)=\cos{\alpha}cos(−α)=cosα
-
sin(π2−α)=cosα\sin(\frac{\pi}{2}-\alpha)=\cos{\alpha}sin(2π−α)=cosα
-
cos(π2−α)=sinα\cos(\frac{\pi}{2}-\alpha)=\sin{\alpha}cos(2π−α)=sinα
-
sin(π2+α)=cosα\sin(\frac{\pi}{2}+\alpha)=\cos{\alpha}sin(2π+α)=cosα
-
cos(π2+α)=−sinα\cos(\frac{\pi}{2}+\alpha)=-\sin{\alpha}cos(2π+α)=−sinα
-
sin(π−α)=sinα\sin{(\pi-\alpha)}=\sin{\alpha}sin(π−α)=sinα
-
cos(π−α)=−cosα\cos{(\pi-\alpha)}=-\cos{\alpha}cos(π−α)=−cosα
-
sin(π+α)=−sinα\sin(\pi+\alpha)=-\sin{\alpha}sin(π+α)=−sinα
-
cos(π+α)=−cosα\cos{(\pi+\alpha)}=-\cos{\alpha}cos(π+α)=−cosα
-
总之,第一象限全是正的,第三象限全是负的
倒数关系
正弦(sine)×余割(co−secant)=1正割(secant)×余弦(co−sine)=1正切(tangent)×余切(co−tangent)=1正弦(sine)\times余割(co-secant)=1 \\正割(secant)\times余弦(co-sine)=1 \\ 正切(tangent)\times余切(co-tangent)=1 正弦(sine)×余割(co−secant)=1正割(secant)×余弦(co−sine)=1正切(tangent)×余切(co−tangent)=1
| tan·gent | co·tan·gent | se·cant | co·se·cant |
|---|---|---|---|
| /ˈtanjənt/ | /kōˈtanjənt/ | /ˈsēˌkant,ˈsēˌkənt/ | /kōˈsēkənt/ |
| 正切 | 余切 | 正割 | 余割 |
六种三角函数间的转换关系
- 正弦余弦&正割余割&正切余切间的转换(π2\frac{\pi}{2}2π)

小结
-
π2−α\frac{\pi}{2}-\alpha2π−α:关于y=xy=xy=x对称
-
关于y=xy=xy=x对称的两点P1=(x1,y1),P2=(x2,y2)P_1=(x_1,y_1),P2=(x_2,y_2)P1=(x1,y1),P2=(x2,y2)坐标关系:
- x1=y2x_1=y_2x1=y2
- x2=y1x_2=y_1x2=y1
Reflections
Shifts and periodicity
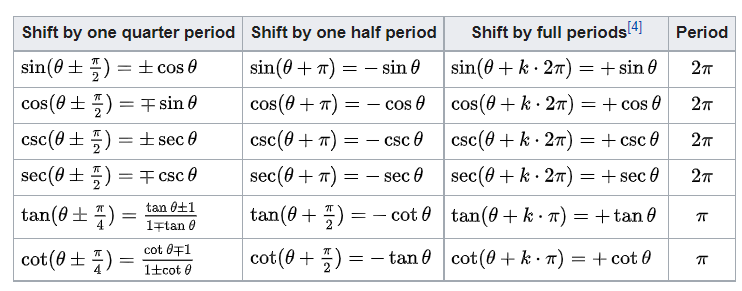
相关文章:
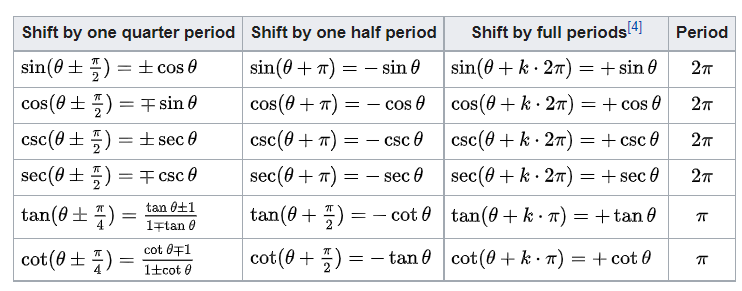
EM@三角函数诱导公式
文章目录诱导公式单位圆坐标和三角函数记忆口诀符号看象限奇变偶不变例常用诱导公式🎈常用部分(5对)倒数关系六种三角函数间的转换关系小结ReflectionsShifts and periodicity诱导公式 诱导公式 - 维基百科,自由的百科全书 (wikipedia.org) 单位圆坐标…...

是不是只能学IT互联网技术才有发展前途?
当然不是,三百六十行,行行出状元。 但我们需要认清一个现实是,我们正处于一个信息爆炸的时代,掌握紧跟潮流的技术,才可以让我们更自信地面对每天的生活,才有多余的精力、财力来享受生活。“人生在世&#…...

Linux 进程:exit和_exit的辨析
目录1.接口与函数2.缓冲区3.exit 与 _exit(1)_exit(2)exit这里来认识exit函数和 _exit接口 ,它们的作用是类似的,都是在调用后退出程序,可以在程序的任何地方调用。 1.接口与函数 exit函数和_exit接口,一个函数,一个…...
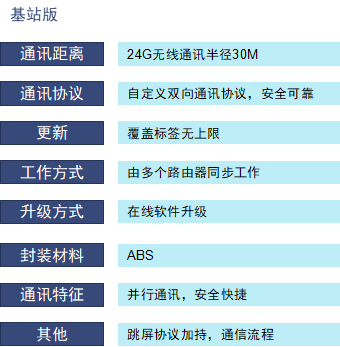
智能电子标签——商超版价签
2.1英寸TFT黑白电子价签 ★ 快速变价,高效运营 ★ 市场实用,布局物联网未来 ★ 更好客户体验 ★ 降低系统成本,具备竞争力 ★ 2.1英寸黑白红电子价签 ★ 电池低能耗,常规使用三年 ★ 穿透力强不慣障碍 ★ 2.4G载波&#x…...
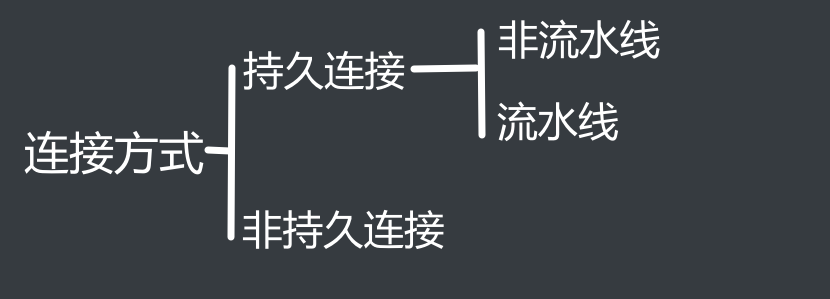
计算机网络自检
1 计网体系结构 因特网结构: 计网三个组成成分: 工作方式-其中2个部分: 功能-两个子网: 5个XAN分别是: 传输技术,两者的主要区别: 4种基本网络拓扑结构: 3种交换技术: 协…...

DC真实数据都有哪些?Filecoin为DC数据存储的解决方案又是什么?
对于生活在数字时代的我们而言,数据或许就和平日呼吸的空气一样,已经不需要我们再去思考其概念。我们的日常生活中无时无刻都有数据的身影,日常的购物消费、出行、学习、记录,当我们每天生活有数字化加持的小区里,工作…...
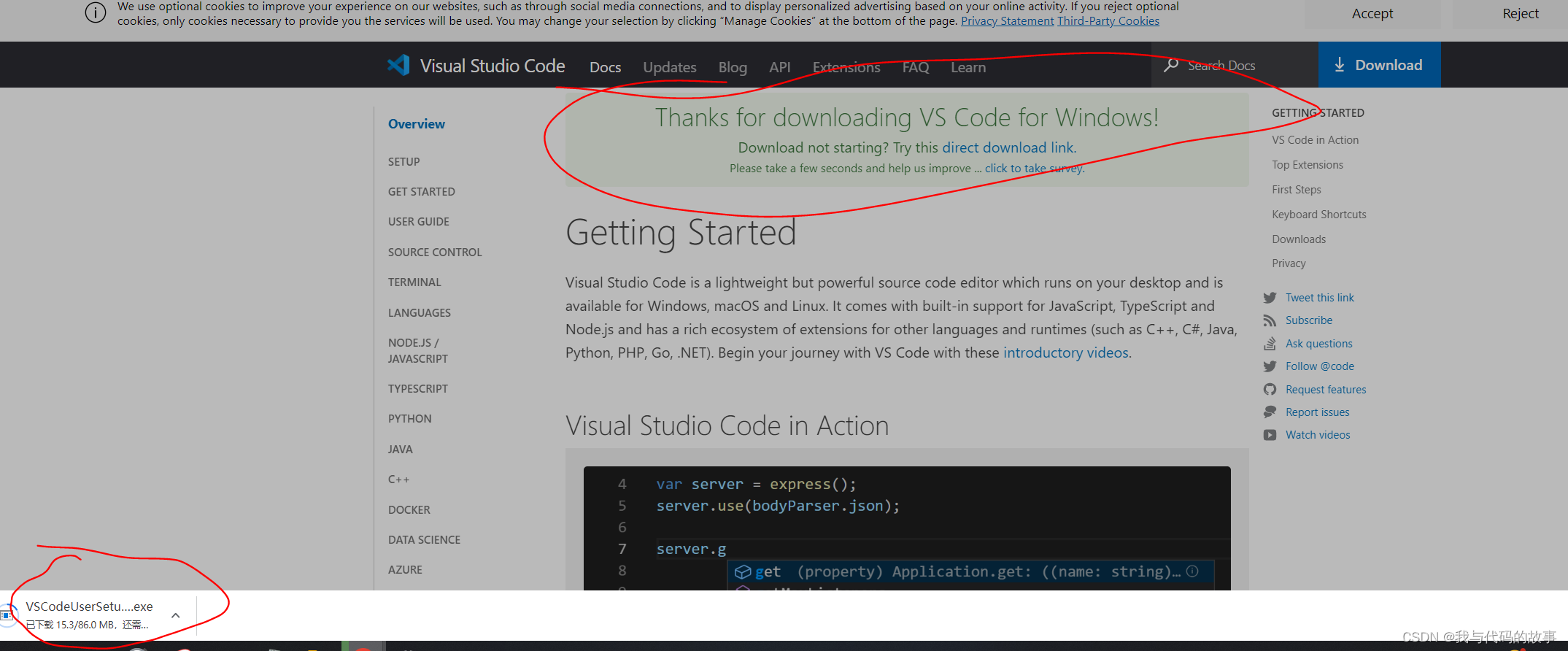
解决vscode无法自动更新
一.前言 要在vscode里面安装插件,被提示版本不匹配,然后得更新,然后我发现我的'帮助'菜单栏下没有检查更新,然后我去&…...

315线上知识竞赛答题活动方案及模板分享
315线上知识竞赛答题活动方案及模板分享在315国际消费者权益日来临之际, 很多单位推出有奖知识竞答, 希望大家在了解专业知识的同时, 还可以拿到自己喜欢的奖品!这是消费者委员会和监管局联合举办的“315消费知识在线有奖竞答”活…...
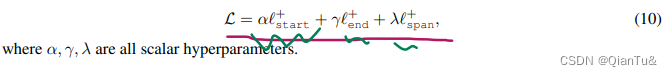
论文复现-2:代码部分
以CONLL03数据集为例 文章目录1 整体框架2 数据结构2.1 原始数据集2.2 处理之后的数据集3 代码部分3.0 模型参数3.1 数据预处理3.2 模型方法3.1.1 定义表示的学习权重项的学习双塔模型3.2.2 forward3.3 损失函数3.4 训练与推理Ablation study训练实例1 整体框架 任务是实体识别…...
Linux开放的端口太多了?教你一招找出所有开放的端口,然后直接干掉!
基于服务器安全性维护的目的,查看所有开放的端口是通常采取的第一步,从中检查出可疑或者不必要的端口并将其关掉。关于查看开放的端口,方法不止一种,比如lsof 命令,还可以使用 ss 命令。 查看开放的端口 今天我们就介…...

mysql集群简介
集群的好处 高可用性:故障检测及迁移,多节点备份。 可伸缩性:新增数据库节点便利,方便扩容。 负载均衡:切换某服务访问某节点,分摊单个节点的数据库压力。 集群要考虑的风险 网络分裂:群集还…...

装饰器模式
概述 当我们编写软件时,有时我们会遇到需要在不修改现有代码的情况下添加新功能的情况。这时,我们可以使用装饰器模式。 装饰器模式是一种结构性设计模式,它允许我们在不改变对象接口的情况下动态地向对象添加功能。装饰器模式通过创建一个…...

21 Nacos客户端本地缓存及故障转移
Nacos客户端本地缓存及故障转移 在Nacos本地缓存的时候有的时候必然会出现一些故障,这些故障就需要进行处理,涉及到的核心类为ServiceInfoHolder和FailoverReactor。 本地缓存有两方面,第一方面是从注册中心获得实例信息会缓存在内存当中&a…...

遍历读取文件夹下的所有文件
遍历读取文件夹下的所有文件 例如,读取文件夹下,子文件夹的所有的jpg文件: import glob path "./database/20230302/night/*/*.jpg"#设置自己的文件夹路径以及文件 image_files glob.glob(path, recursiveTrue)for image_file …...
nexus安装与入门
安装 nexus-3.31.1-01-unix.tar.gz 链接:https://pan.baidu.com/s/1YrJMwpGxmu8N2d7XMl6fSg 提取码:kfeh 上传到服务器,解压 tar -zvxf nexus-3.31.1-01-unix.tar.gz进入bin目录,启动 ./nexus start查看状态 ./nexus status默…...
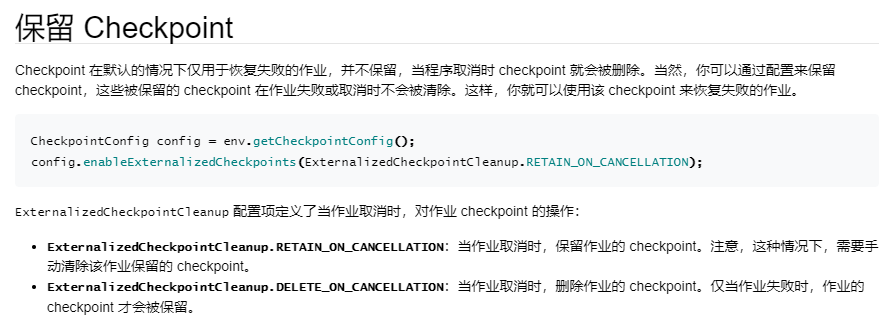
Flink SQL Checkpoint 学习总结
前言 学习总结Flink SQL Checkpoint的使用,主要目的是为了验证Flink SQL流式任务挂掉后,重启时还可以继续从上次的运行状态恢复。 验证方式 Flink SQL流式增量读取Hudi表然后sink MySQL表,任务启动后处于running状态,先查看sin…...
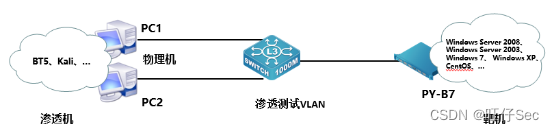
2023年“楚怡杯“湖南省职业院校技能竞赛“网络安全”竞赛任务书
2023年“楚怡杯“湖南省职业院校技能竞赛“网络安全”竞赛任务书 一、竞赛时间 总计:360分钟 竞赛阶段竞赛阶段 任务阶段 竞赛任务 竞赛时间 分值 A模块 A-1 登录安全加固 180分钟 200分 A-2 本地安全策略配置 A-3 流量完整性保护 A-4 事件监控 …...

MyBatis中主键回填的两种实现方式
主键回填其实是一个非常常见的需求,特别是在数据添加的过程中,我们经常需要添加完数据之后,需要获取刚刚添加的数据 id,无论是 Jdbc 还是各种各样的数据库框架都对此提供了相关的支持,本文我就来和和大家分享下数据库主…...

Windows11如何打开ie浏览器
目录1.背景:2.方法一:在 edge 中配置使用 ie 模式3.方法二:通过 Internet 选项 打开1.背景: 昨天电脑自动从win10升级为win11了,突然发现电脑找不到ie浏览器了,打开全都是直接跳转到 edge 浏览器࿰…...

Linux:进程间通信
目录 进程间通信目的 进程间通信分类 管道 System V IPC POSIX IPC 什么是管道 站在文件描述符角度-深度理解管道 管道使用 管道通信的四种情况 管道通信的特点 进程池管理 命名管道 创建一个命名管道 命名管道的打开规则 命名管道通信实例 匿名管道与命名管道的…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

