1.4.1机器学习——梯度下降+α学习率大小判定
1.4.1梯度下降
4.1、梯度下降的概念
※【总结一句话】:系统通过自动的调节参数w和b的值,得到最小的损失函数值J。
如下:是梯度下降的概念图。
-
我们有一个损失函数 J(w,b),包含两个参数w和b(你可以想象成J(w,b) = w*x + b) ,我们想要找到最合适的w和b,尝试最小化损失函数 J(w,b)的值
-
”梯度下降“:梯度下降(gradient descent)在机器学习中应用十分的广泛,不论是在线性回归还是Logistic回归中,它的主要目的是通过迭代找到目标函数的最小值,或者收敛到最小值。
-
它还适用于有多个参数的(如图:w1~ wn,b) :梯度下降的任务是调节w1 ~ wn 和 参数 b 的值,最小化损失函数的值
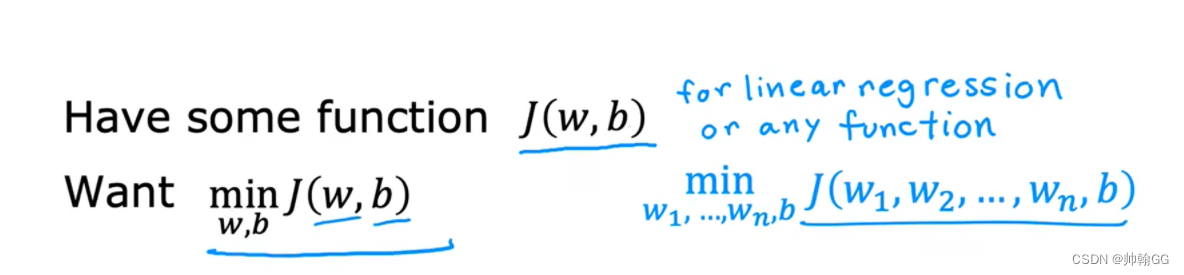
- 梯度下降法是用来计算损失函数最小值的。它的思路很简单,想象在山顶放了一个球,一松手它就会顺着山坡最陡峭的地方滚落到谷底:
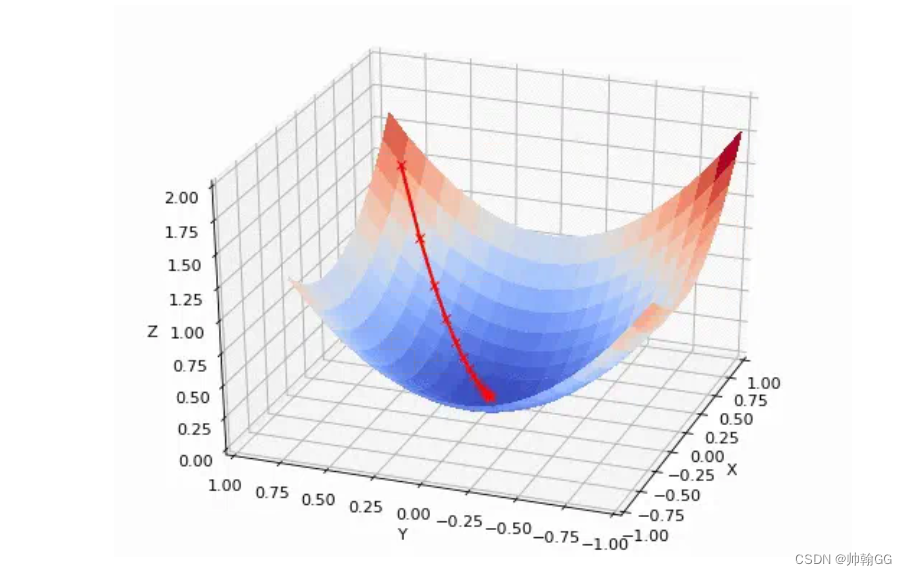
4.2、梯度下降概述

- J(w,b) = wx + b : 我们开始的时候w和b可以设置为任意值。(这里我们设置 w=0 , b = 0)
- “梯度下降”要做的就是:通过迭代不断的调整 w和b 的值,去尽量的降低损失函数J(w,b)
- 直到我们的损失函数J(w,b) 达到/接近 “谷底”/最小值
- 【※注意】 :损失函数可能不仅仅是一个如右图的抛物线,也可能是“高尔夫球场图”,这样的话minimum最小值的个数就不仅仅是一个了
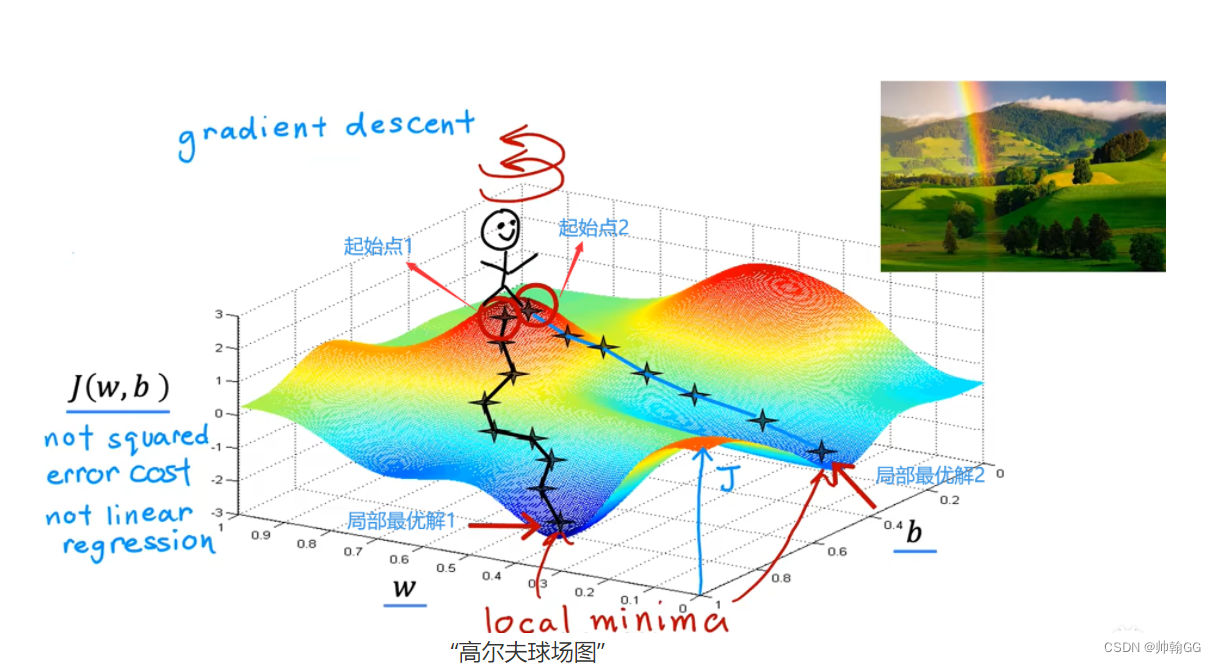
“高尔夫球场图”
-
图中XYZ轴分别代表:W,b , 损失函数 J(w,b)的值
-
他不是一个 “平方误差损失函数”(线性回归使用 平方误差损失函数)图,因为 “平方误差损失函数”常常以抛物线 / 吊床 的形状结束
-
这个小人站在哪的起始点取决于你选择的参数w 和 b的起始值
-
两个谷底最低点都是局部最优解
1.4.2 理解梯度下降+梯度下降偏导的意义+α学习率
- 图解定义:

- 对梯度下降公式算法的解读:
- 其中参数 w和b 是一个同步进行 修改/微调 的。(同步进行,就是计算w和b的更新的两个公式是同步计算 的)
- 重复以上两个公式,直到达到结果收敛为止
- 在收敛重复这个公式的过程中,在计算tmp_w 和tmp_b中 的w是上一次迭代的w的值,只有tmp_w 和tmp_b都计算完成才会进行更新
- 你可能存在疑问:为什么不要用中间值 tmp_w 和wmp_b,直接就是 w = w - α…;b= b - α…不行吗???
- 答:你提问的很好。但是在这个梯度下降w,b迭代执行过程中,w和b同时参与了w,b的计算。
- 简单的说如下图,以W为例,加入在第i次迭代的情况下:
- 在第i次迭代的情况下执行完第一步w = w -0.2 后(假设这时候 J(w,b) = 0.2),
- 执行第二步 b = b - J(w,b) 的时候,你想放 执行w = w -0.2 更新之前的值 or 更新之后的值???
- 每一次迭代,在这第i次中,w 和 b对应的是第i -1次的值,在第i次迭代结束时才一起更新
- 如果不借用中间值 tmp_w 和 tmp_b,那么w 和 b 的最终值 就会受到影响

为了方便理解α(学习率),我们这里把b设置为0,只考虑有w的一维情况
-
其中α:称为学习率(粉色框内容),通常这个值在 0~1 之间,是控制w和b的调参步长
- 合适:
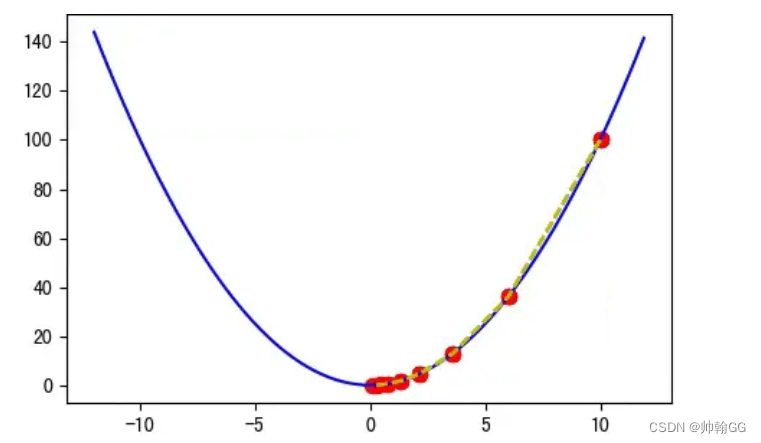
过程解释:
红框中:是求w的偏导,这里求完偏导知道是>0
α永远是 大于0 小于1 的数
然后w = w - α(正数) ====> w变小
所以就实现了微调
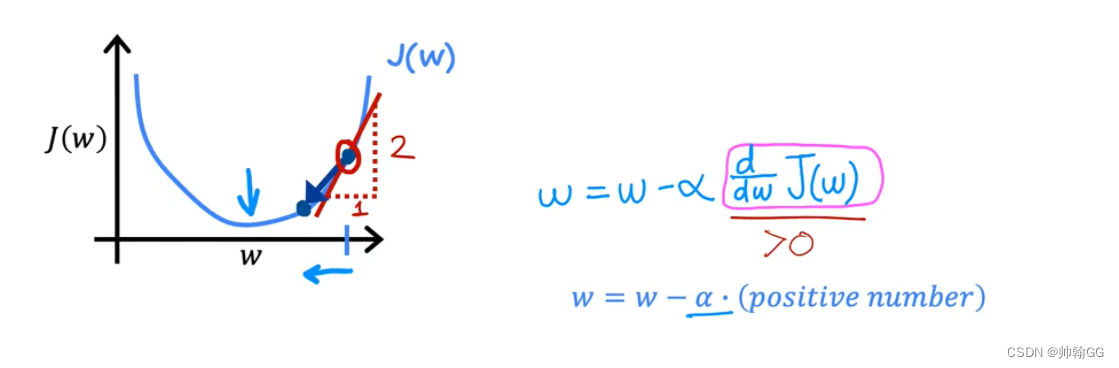
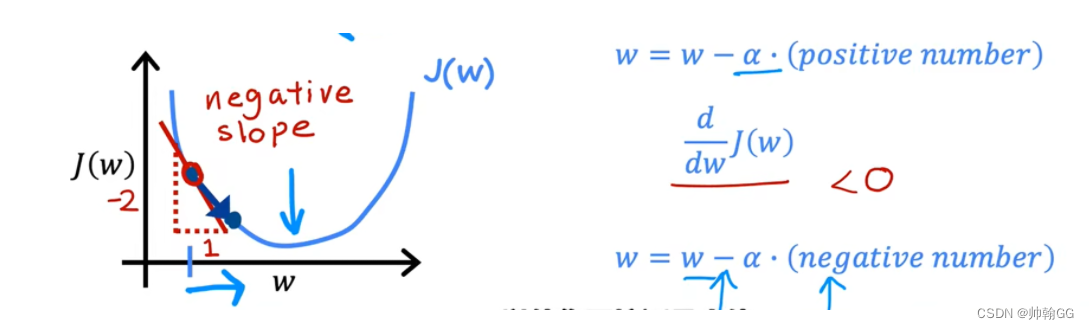
当W的偏导< 0 时:
红框中:是求w的偏导,这里求完偏导知道是<0α永远是 大于0 小于1 的数
然后w = w - α(负数) ====> w变大
所以就实现了微调.
-
如果α非常大:那么这个是一个非常激进的梯度下降的过程,步长会非常大,反而会越过谷底,不断上升:+
-
动图地址
](https://img-blog.csdnimg.cn/direct/c8bcf0eb4eb141909ef1434038f1ce89.png)
吴恩达老师的解释:
如果α过大/过大的步长:
会导致超过 , 并且从来不会达到最小值。
不能直线收敛,甚至是发散
- 合适:

-
如果α非常小:比如 α = 0.0001 就过于小了,迭代 20 次后离谷底还很远,实际上 100 次后都无法到达谷底:
梯度下降会起作用,但是需要很长的时间
-
动图地址
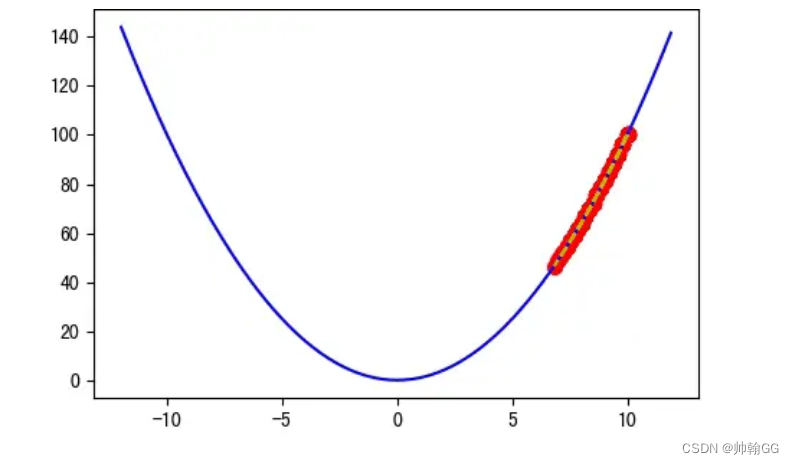
吴恩达的解释:
如果α 步长太小,会实现收敛,但是这个收敛的过程会很慢很慢
- **总结:**不同的步长α ,随着迭代次数的增加,会导致被优化函数f(x) 的值有不同的变化:

关于α选择以及判定的 详细内容看: 2.2.3机器学习—— 判定梯度下降是否收敛 + α学习率的选择
1.4.3 用于线性回归的梯度下降
-
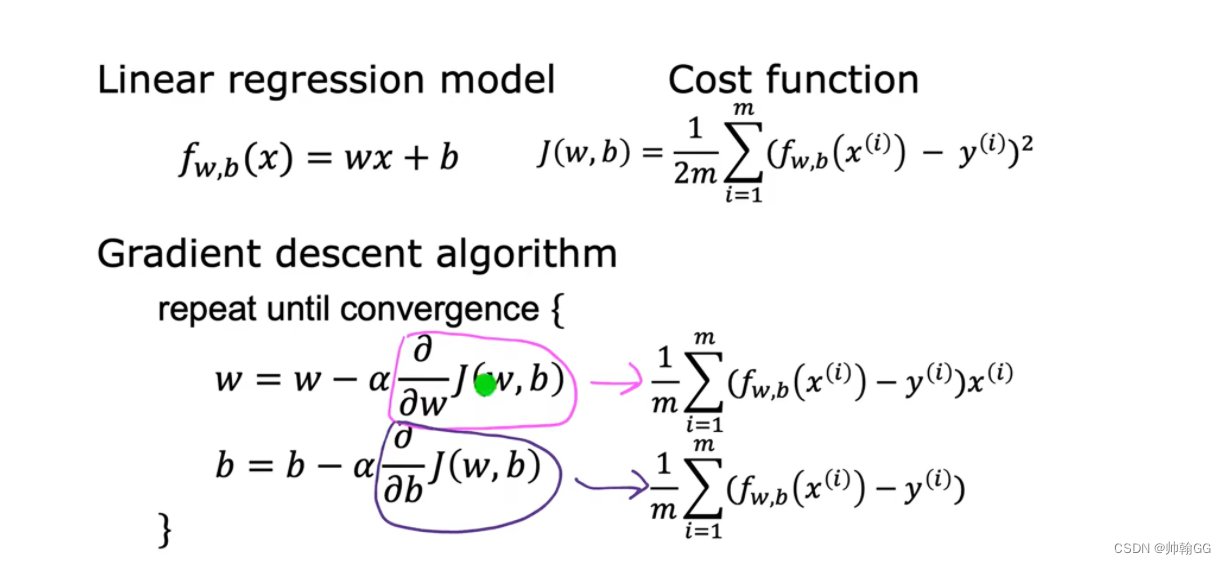
公式推到来源:
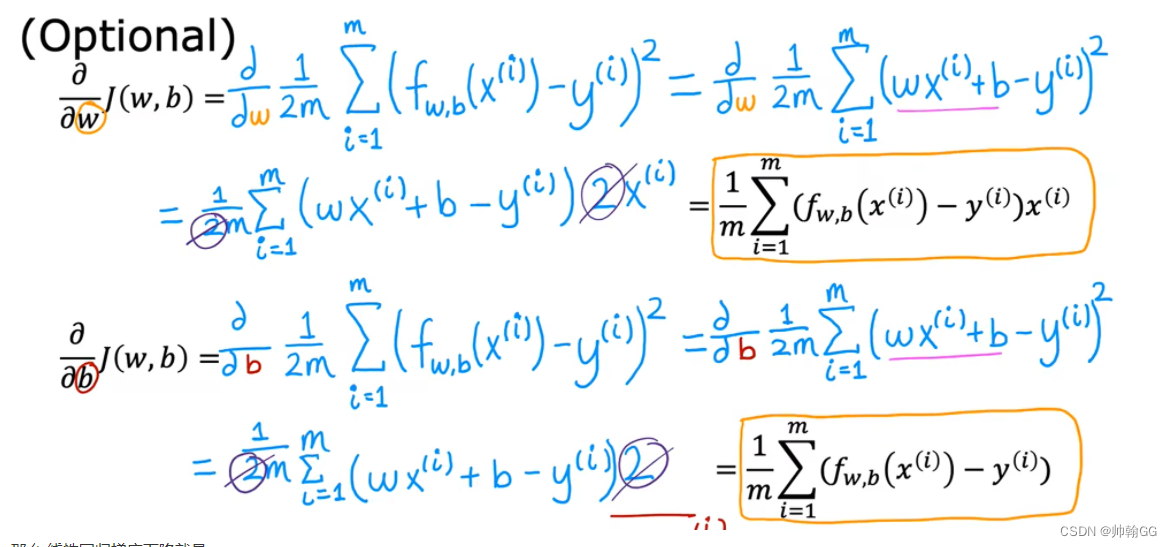
-
那么 线性回归梯度下降就是:
重复对w 和 b 执行更新直到收敛
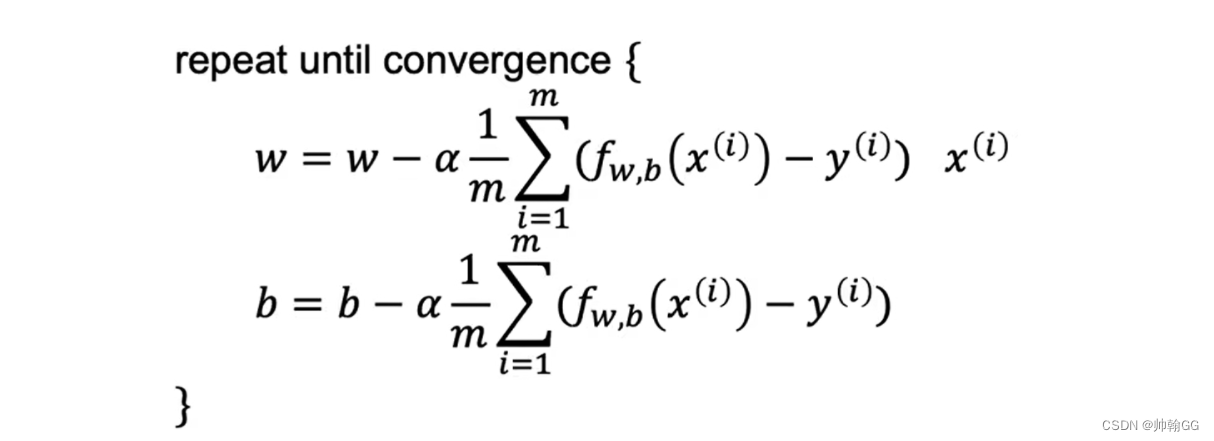
- 当使用线性回归的平方误差损失函数时,全局只有一个最低点
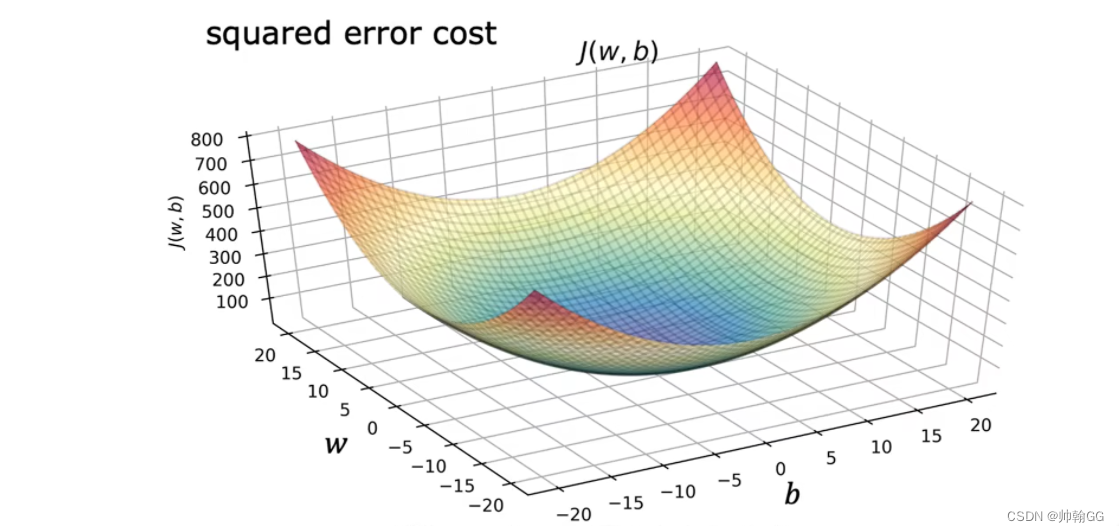
- 当使用非平方误差函数时,就是非线性回归梯度下降的时候就会出现 >=1 的局部最优解
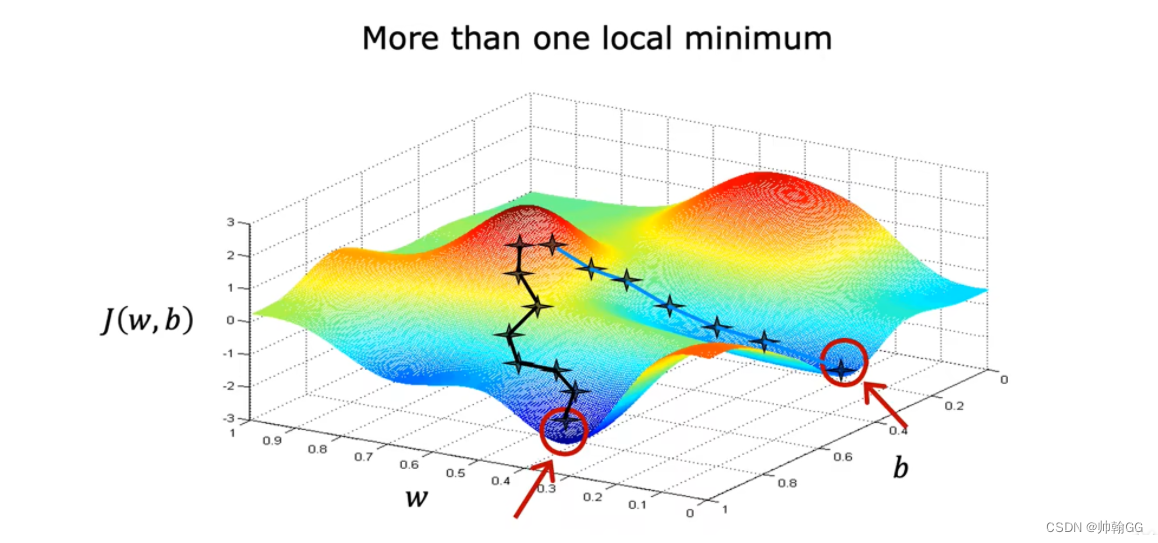
1.4.4 线性回归的梯度下降的应用
- 等高线最中心那个圈是 损失函数值最小的点,Cost值越小,说明线性回归的拟合越好,直到我们达到全局最小值
- 比如当 Size in feet 是1250 ,对应的回归预测值是 250 K
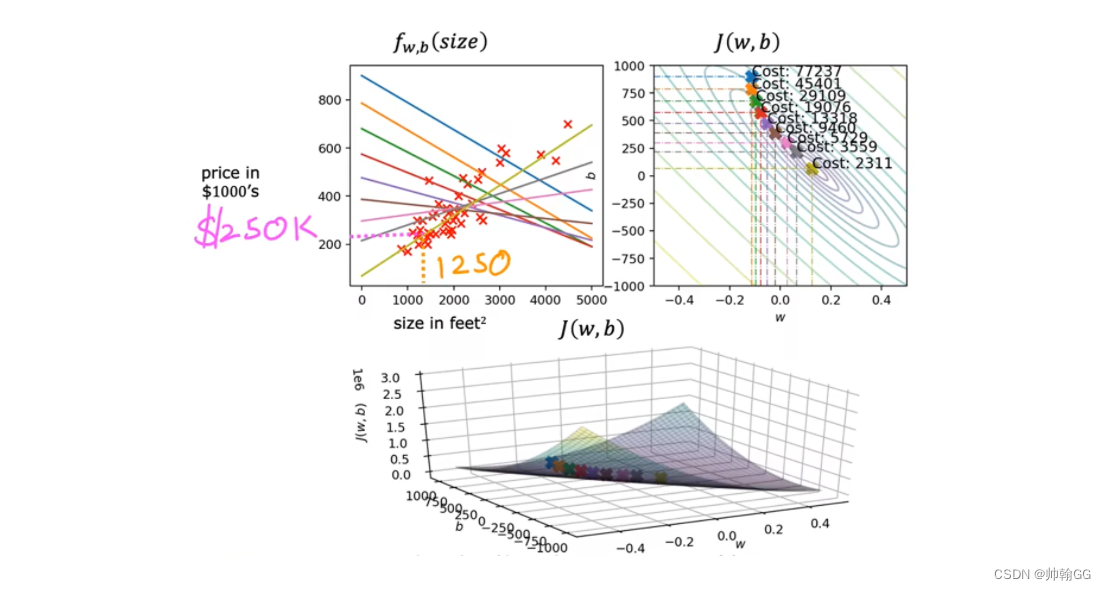
- “批量梯度下降”:每一次的梯度下降使用的是全部的训练的数据:
- 当计算 w 和 b 的偏导时,我们从 1 ~ m 所有的数据都计算上,然后相加求平均

※1.4.5 线性回归的梯度下降函数的代码实现
1、求损失函数
求损失函数代码如下:
def compute_cost(x, y, w, b): """Computes the cost function for linear regression.Args:x (ndarray (m,)): Data, m examples y (ndarray (m,)): target valuesw,b (scalar) : model parameters Returnstotal_cost (float): The cost of using w,b as the parameters for linear regressionto fit the data points in x and y"""# number of training examplesm = x.shape[0] cost_sum = 0 for i in range(m): f_wb = w * x[i] + b cost = (f_wb - y[i]) ** 2 cost_sum = cost_sum + cost total_cost = (1 / (2 * m)) * cost_sum return total_cost
2、求偏导 / 梯度
※求偏导代码如下:
def compute_gradient(x, y, w, b): """Computes the gradient for linear regression Args:x (ndarray (m,)): Data, m examples y (ndarray (m,)): target valuesw,b (scalar) : model parameters Returnsdj_dw (scalar): The gradient of the cost w.r.t. the parameters wdj_db (scalar): The gradient of the cost w.r.t. the parameter b """# Number of training examplesm = x.shape[0] dj_dw = 0dj_db = 0for i in range(m): f_wb = w * x[i] + b dj_dw_i = (f_wb - y[i]) * x[i] dj_db_i = f_wb - y[i] dj_db += dj_db_idj_dw += dj_dw_i dj_dw = dj_dw / m dj_db = dj_db / m return dj_dw, dj_db
3、梯度下降函数
def gradient_descent(x, y, w_in, b_in, alpha, num_iters, cost_function, gradient_function): """Performs gradient descent to fit w,b. Updates w,b by taking num_iters gradient steps with learning rate alphaArgs:x (ndarray (m,)) : Data, m examples y (ndarray (m,)) : target valuesw_in,b_in (scalar): initial values of model parameters alpha (float): Learning ratenum_iters (int): number of iterations to run gradient descentcost_function: function to call to produce costgradient_function: function to call to produce gradientReturns:w (scalar): Updated value of parameter after running gradient descentb (scalar): Updated value of parameter after running gradient descentJ_history (List): History of cost valuesp_history (list): History of parameters [w,b] """w = copy.deepcopy(w_in) # avoid modifying global w_in# An array to store cost J and w's at each iteration primarily for graphing laterJ_history = []p_history = []b = b_inw = w_infor i in range(num_iters):# Calculate the gradient and update the parameters using gradient_functiondj_dw, dj_db = gradient_function(x, y, w , b) # Update Parameters using equation (3) aboveb = b - alpha * dj_db w = w - alpha * dj_dw # Save cost J at each iterationif i<100000: # prevent resource exhaustion J_history.append( cost_function(x, y, w , b))p_history.append([w,b])# Print cost every at intervals 10 times or as many iterations if < 10if i% math.ceil(num_iters/10) == 0:print(f"Iteration {i:4}: Cost {J_history[-1]:0.2e} ",f"dj_dw: {dj_dw: 0.3e}, dj_db: {dj_db: 0.3e} ",f"w: {w: 0.3e}, b:{b: 0.5e}")return w, b, J_history, p_history #return w and J,w history for graphing
※※关于α选择以及判定的 详细内容看: 2.2.3机器学习—— 判定梯度下降是否收敛 + α学习率的选择
相关文章:

1.4.1机器学习——梯度下降+α学习率大小判定
1.4.1梯度下降 4.1、梯度下降的概念 ※【总结一句话】:系统通过自动的调节参数w和b的值,得到最小的损失函数值J。 如下:是梯度下降的概念图。 我们有一个损失函数 J(w,b),包含两个参数w和b(你可以想象成J(w,b) w*x…...

在IntelliJ IDEA中,.idea文件是什么,可以删除吗
相信有很多小伙伴,在用idea写java代码的时候,创建工程总是会出现.idea文件,该文件也从来没去打开使用过,那么它在我们项目里面,扮演什么角色,到底能不能删除它呢? 1、它是什么?有什么…...

【Spring Cloud】Gateway组件的三种使用方式
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是Java方文山,一个在CSDN分享笔记的博主。📚📚 🌟推荐给大家我的专栏《Spring Cloud》。🎯🎯 &am…...

对象的复制
方式一:sv 的new函数 trans tr1,tr2; malbox.get(tr2); tr1 new tr2;//仅用于浅拷贝,拷贝后tr1,tr2为两个独立的对象方式二:uvm 域的自动化常用函数:copy / clone / 使用前提: 1. 函数都可用于uvm_object类型&…...
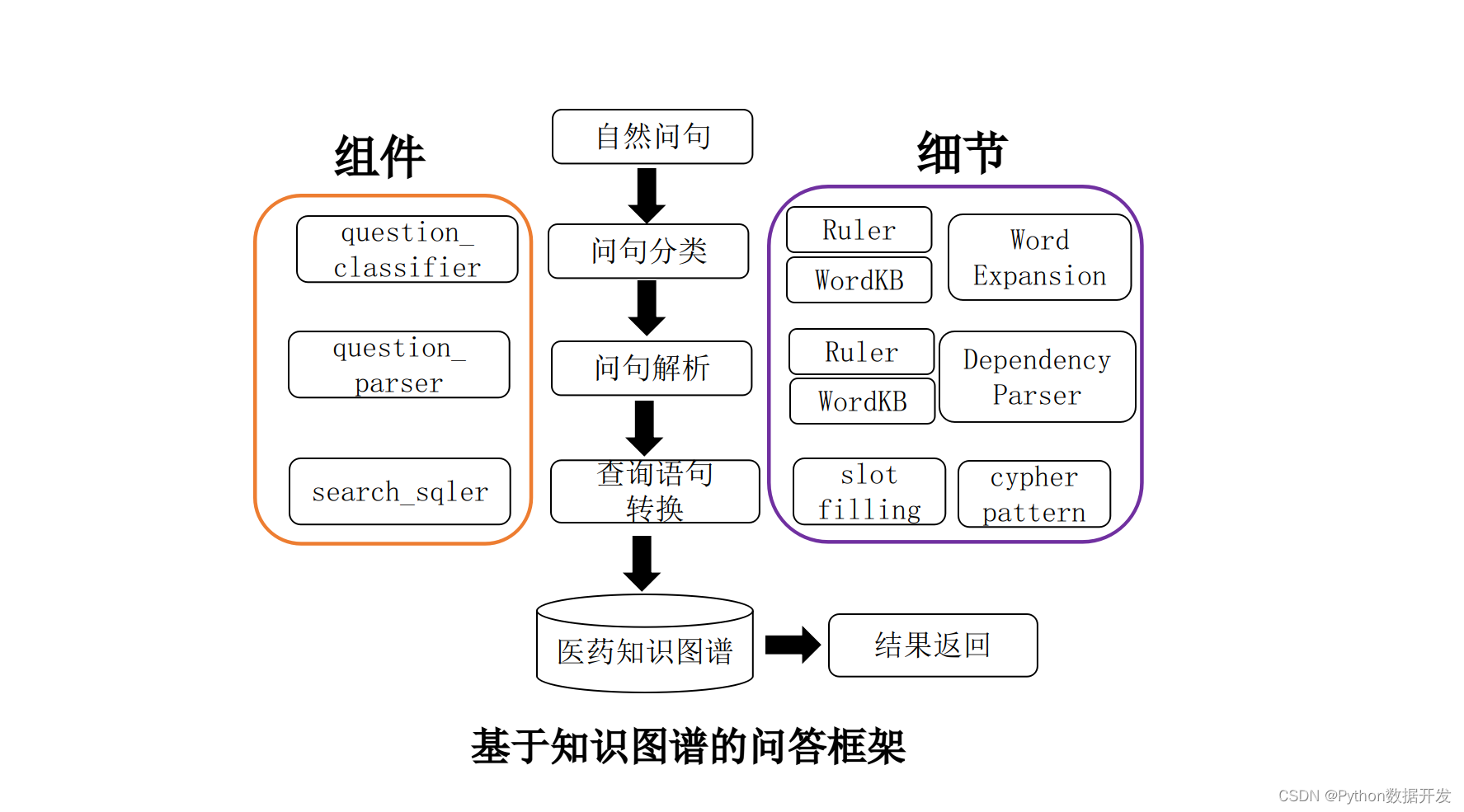
基于 Python+Neo4j+医药数据,构建了一个知识图谱的自动问答系统
知识图谱是目前自然语言处理的一个热门方向。目前知识图谱在各个领域全面开花,如教育、医疗、司法、金融等。 本项目立足医药领域,以垂直型医药网站为数据来源,以疾病为核心,构建起一个包含7类规模为4.4万的知识实体,…...
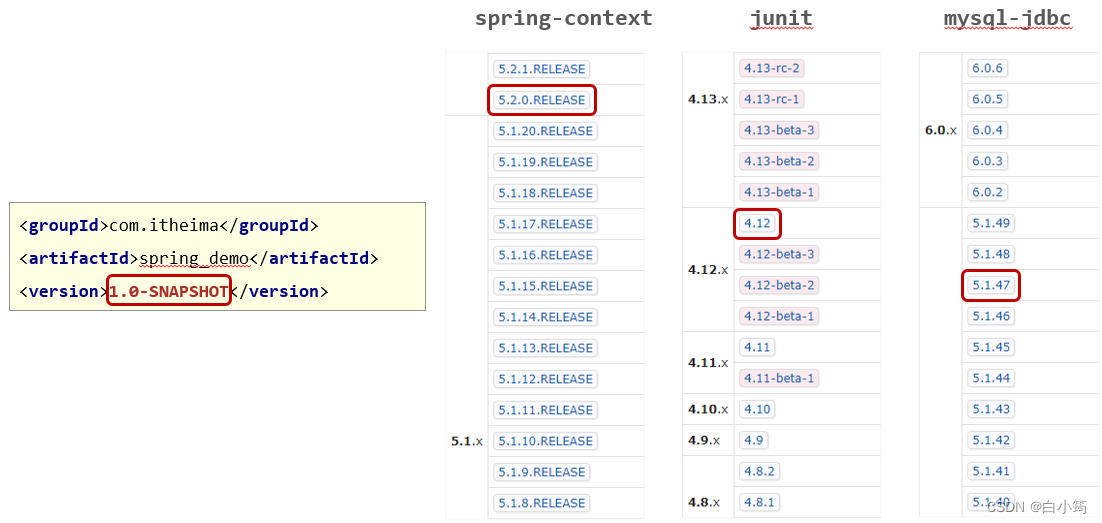
Maven之属性管理
1.属性管理 1.1 属性配置与使用 ①:定义属性 <!--定义自定义属性--> <properties><spring.version>5.2.10.RELEASE</spring.version> </properties>②:引用属性 <dependency><groupId>org.springframewor…...
快乐学Python,数据分析之获取数据方法「公开数据或爬虫」
学习Python数据分析,第一步是先获取数据,为什么说数据获取是数据分析的第一步呢,显而易见:数据分析,得先有数据,才能分析。 作为个人来说,如何获取用于分析的数据集呢? 1、获取现成…...

前端常用的设计模式
设计模式:是一种抽象的编程思想,并不局限于某一特定的编程语言,而是在许多语言之间是相通的;它是软件设计中常见的问题的通用、可反复使用、多少人知晓的一种解决方案或者模板。一般对与从事过面向对象编程的人来说会更熟悉一些。…...

游戏引擎支持脚本编程有啥好处
很多游戏引擎都支持脚本编程。Unity、Unreal Engine、CryEngine等大型游戏引擎都支持使用脚本编写游戏逻辑和功能。脚本编程通常使用C#、Lua或Python等编程语言,并且可以与游戏引擎的API进行交互来控制游戏对象、设置变量、执行行为等。使用脚本编程,游戏…...
)
react中概念性总结(二)
目录 说说你对react的理解?有哪些特性? 说说Real diff算法是怎么运作的,从tree层到component层到element层分别讲解? 调和阶段setState干了什么? 说说redux的工作流程? 为什么react元素有一个$$type属…...
WPF自定义漂亮顶部工具栏 WPF自定义精致最大化关闭工具栏 wpf导航栏自定义 WPF快速开发工具栏
在WPF应用程序开发中,自定义一个漂亮的顶部工具栏具有多重关键作用,它不仅增强了用户体验,还提升了整体应用的专业性和易用性。以下是对这一功能的详细介绍: 首先,自定义顶部工具栏是用户界面设计的重要组成部分&…...
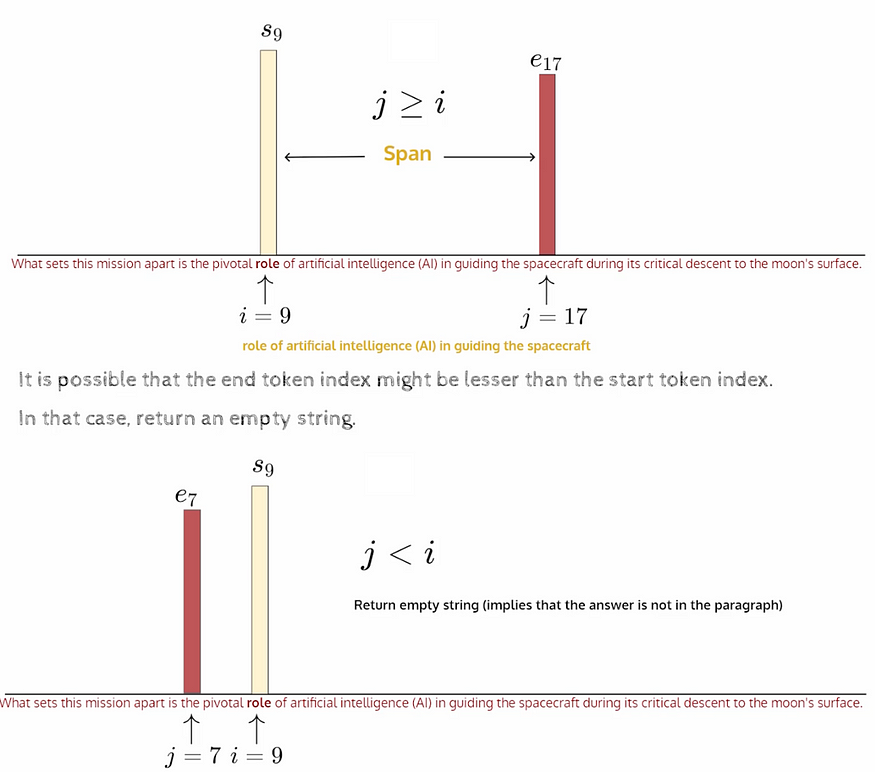
Transformer 的双向编码器表示 (BERT)
一、说明 本文介绍语言句法中,最可能的单词填空在self-attention的表现形式,以及内部原理的介绍。 二、关于本文概述 在我之前的博客中,我们研究了关于生成式预训练 Transformer 的完整概述,关于生成式预训练 Transformer (GPT) 的…...
关于LwRB环形缓冲区开源库的纯C++版本支持原子操作
1、LwRB环形缓冲区开源库: GitHub - MaJerle/lwrb: Lightweight generic ring buffer manager libraryLightweight generic ring buffer manager library. Contribute to MaJerle/lwrb development by creating an account on GitHub.https://github.com/MaJerle/l…...
微信小程序Canvas画布绘制图片、文字、矩形、(椭)圆、直线
获取CanvasRenderingContext2D 对象 .js onReady() {const query = wx.createSelectorQuery()query.select(#myCanvas).fields({ node: true, size: true }).exec((res) => {const canvas = res[0].nodeconst ctx = canvas.getContext(2d)canvas.width = res[0].width * d…...

Unity Editor实用功能:Hierarchy面板的对象上绘制按按钮并响应
目录 需求描述上代码打个赏吧 需求描述 现在有这样一个需求: 在Hierarchy面板的对象上绘制按钮点击按钮,弹出菜单再点击菜单项目响应自定义操作在这里的响应主要是复制对象层级路路径 看具体效果请看动图: 注: 核心是对Edito…...
解决录制的 mp4 视频文件在 windows 无法播放的问题
解决录制的 mp4 视频文件在 windows 无法播放的问题 kazam 默认录制保存下来的 mp4 视频文件在 windows 中是无法直接使用的,这是由于视频编码方式的问题。解决办法: 首先安装 ffmeg 编码工具: sudo apt-get install ffmpeg 然后改变视频的…...

一键与图片对话!LLM实现图片关键信息提取与交互
本期文心开发者说邀请到飞桨开发者技术专家徐嘉祁,主要介绍了如何通过小模型与大模型的结合,解决数据分析中的问题。 项目背景 在智能涌现的大模型时代,越来越多的企业和研究机构开始探索如何利用大模型来提升工作效率,助力业务智…...

洛谷 P8833 [传智杯 #3 决赛] 课程 讲解
前言: 大家好! 我们又见面啦~~~ 对于我20多天没上号,深表歉意!! 希望大家给我的account点一个赞,加一个粉丝,谢谢! 也对CSDN的所有博主们送上衷心的祝福! 如有错误…...

中国IT产经新闻:新能源汽车发展前景与燃油车的利弊之争
随着科技的进步和环保意识的提高,新能源汽车在全球范围内逐渐受到重视。然而,在新能源汽车迅速发展的同时,燃油车仍然占据着主导地位。本文将从新能源与燃油车的利弊、新能源汽车的发展前景两个方面进行分析,以期为读者提供全面的…...

一、数据结构
一、 数组 1.1 数组 定义 遍历 // 遍历数组 传递指针 func traverse() {var b [...]int{1, 2, 3} //长度为3 元素为 1 2 3var ptr &b //ptr是指向数组的指针fmt.Println(b[0], b[1]) // 打印数组的前 2 个元素fmt.Println(ptr[0], ptr[1]) // 通…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...
