leetcode滑动窗口问题总结 Python
目录
一、理论
二、例题
1. 最长无重复字符串
2. 长度最小的子数组
3. 字符串的排列
4. 最小覆盖子串
5. 滑动窗口最大值
一、理论
滑动窗口是一类比较重要的解题思路,一般来说我们面对的都是非定长窗口,所以一般需要定义两个指针 left 和 right,分别用来限制窗口的左边界和右边界。在解题时一般需要设定两个嵌套的循环,外循环不设定条件,完全是遍历模式,驱动右指针的移动;内循环需要设定条件,在满足条件的情况下,驱动左指针的移动。整体实现滑动窗口的向右移动。外循环虽然没有设定条件,但其实存在隐藏的条件就是不满足内循环所设定的条件时运行。在这个框架下,我们可以增加对窗口长度和数据的记录,进而实现丰富的功能。
def fun():left = 0 # 定义左指针right = 0 # 定义右指针length = 0 # 记录窗口长度# 可以定义数据结构记录窗口元素,例如set(), set().add(), set.remove()while right < len(s): # 首先移动右指针length += 1 # 每移动一次右指针,窗口长度加一# 可以做一下数据操作,例如set().add()while check(): # 满足某个条件下移动左指针# 可以做一下数据操作,例如set().remove()left += 1 # 然后移动左指针length -= 1 # 每一定一次左指针,窗口长度减一right += 1 # 真正移动右指针return 二、例题
1. 最长无重复字符串
给定一个字符串 s ,请你找出其中不含有重复字符的最长子串的长度。
示例:
输入: s = "abcabcbb"
输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
该问题可以使用动态规划的思想来解,具体可以看leetcode动态规划问题总结 Python,本题还可以使用变长滑动窗口的思路来解。定义两个指针 left 和 right,以及一个集合 lookup,lookup 表示以右指针 right 为结尾的最长无重复字符串集合,实时更新 left、right 和 lookup。然后向右移动右指针(隐藏条件是 s[right] 不存在于 lookup),直至 s[right] 存在于 lookup,然后固定右指针,右移左指针,直至 s[right] 不存在于 lookup。该双指针移动的结果是完备的,当移动右指针时,可以保证同步左移左指针一定会造成出现重复字符,若同步右移左指针则会造成无重复字符串变短,并小于已找到的无重复字符串,所以右指针右移过程中并没有错过任何有用的无重复字符串。当右指针固定,右移左指针时也是完备的,此时如果左移则不会生成新的无重复字符串,所以没必要,但如果 s[right] 不存在于 lookup 时,还继续右移左指针,会造成无重复字符串变短,并小于已找到的无重复字符串,所以也没有必要继续右移。思路确定好了以后,就可以通过滑动窗口的两个循环嵌套实现编程,外层循环控制右指针递增右移,不用设定判断条件(其实存在隐含判断条件,就是与内层判断条件相反),内层循环需要设定判断条件,内层循环还需要控制左指针的右移。
def lengthOfLongestSubstring(s):if not s: return 0left = 0lookup = set()n = len(s)max_len = 0cur_len = 0for i in range(n):cur_len += 1while s[i] in lookup:lookup.remove(s[left])left += 1cur_len -= 1if cur_len > max_len: max_len = cur_lenlookup.add(s[i])return max_len2. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。找出该数组中满足其总和大于等于 target 的长度最小的连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2 解释:子数组 [4,3] 是该条件下的长度最小的子数组。
该问题属于变长滑动窗口问题,定义两个指针 start 和 end。在子串求和小于 target 时,end 向右移动,直至子串求和大于等于 target,然后固定 end,右移 start,直至子串求和小于 target,然后再次移动 start,循环往复。该种移动方式的解是完备的,只是缩小了解的搜索范围,所以时间复杂度更优。在右移 end 时,子串求和小于 target,如果左移 start,虽然有可能得到求和大于 target 的子串,但是这些子串的长度一定大于已找到的子串,所以并不属于所求解的范围,亦或者根本无法左移 start(=0),此时如果右移 start,那所有子串的和都小于 target,所以也不属于求解的范围。在 end 固定时,如果左移 start,依然不属于求解范围,因为窗口长度会增加,超过了现有解的长度,只能右移 start,右移至子串求和小于 target 后就不能再右移了,因为继续右移不可能找到子串求和大于 target 的解。编程思路是两层循环嵌套,外层循环控制 end 的移动,隐藏条件是子串求和小于 target,内层循环控制 start 的移动,判断条件是子串求和大于等于 target。
def minSubArrayLen(s, nums):if not nums:return 0n = len(nums)ans = n + 1start, end = 0, 0total = 0while end < n:total += nums[end]while total >= s:ans = min(ans, end - start + 1)total -= nums[start]start += 1end += 1return 0 if ans == n + 1 else ans3. 字符串的排列
给你两个字符串 s1 和 s2 ,写一个函数来判断 s2 是否包含 s1 的排列。如果是,返回 true ;否则,返回 false 。换句话说,s1 的排列之一是 s2 的子串 。
示例:
输入:s1 = "ab" s2 = "eidbaooo"
输出:true 解释:s2 包含 s1 的排列之一 ("ba").
该问题属于定长滑动窗口问题,以一个固定长度 len(s1) 进行滑动,所以该问题的核心问题在于,怎么判断一个长度为 len(s1) 的子集是否为 s1 的排列,这里采用的方式是通过字典统计每个字符出现的频率,然后比较两个字典是否相等,如果相等,则两个字符串互为排列。当窗口滑动时,只需要将新加入的字符添加到字典中,同步将剔除的字符从字典中剔除即可。
def checkInclusion(s1, s2):l1 = len(s1)l2 = len(s2)if l2 < l1: # 若字符串s2的长度小于s1,则返回falsereturn Falses = 'abcdefghijklmnopqrstuvwxyz'dict1 = {}dict2 = {}for char in s:dict1[char] = 0 # 初始化字典,key为字母,value为字母出现的次数,都初始化为0dict2[char] = 0for i in range(l1):dict1[s1[i]] += 1 # 首先计算前l1长度的不同字母出现次数dict2[s2[i]] += 1if dict1 == dict2: # 若两个字典相等,则说明字符串的[0:l1]是字符串l1的不同排列return Truefor i in range(l2-l1): # 开始往后查找,每次移动一个位置dict2[s2[i]] -= 1 # 减去滑动比较得前一个字母出现的次数dict2[s2[i+l1]] += 1 # 加上滑动后加进来的字母出现的次数if dict1 == dict2: # 若相等,则返回truereturn Truereturn False4. 最小覆盖子串
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 " " 。注意:对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。如果 s 中存在这样的子串,我们保证它是唯一的答案。
示例:
输入:s = "ADOBECODEBANC", t = "ABC"
输出:"BANC" 解释:最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。
该问题采用滑动窗口的思路来解,定义左右两个指针,均起于 0 位置,右指针在滑动窗口不包含 t 字符串的情况下向右移动,当右指针使得滑动窗口包含 t 时,固定右指针,右移左指针,直至滑动窗口不包含 t 字符串,然后固定左指针,再次右移右指针,循环往复,直至右指针达到最右侧。该逻辑是完备的,当右指针右移时,起初如果不左移左指针,那滑动窗口并不包含 t 字符串,所以没必要检查每个路过的字符以及每个字符对应的所有可能字符串,如果左移左指针,会造成字符串长度增加,也不可能被使用,所以右指针右移时并没有错过满足条件的解。当滑动窗口包含 t 字符串时,左指针右移,也是完备的,左指针没必要左移,因为左移会增加子集的长度,而我们已经有更短的满足条件的解,所以左指针只能右移,当右移至滑动窗口不包含 t 字符串时,停止右移,因为继续右移只会得到一堆不满足条件的子集。所以实际右指针针对大部分字符仅仅只是检查了一次,针对剩余的小批量字符也只是检查了很少一部分对应字符串,整体算下来,左右指针的时间复杂度都是O(N)级别,如果是暴力法,那仅仅获取所有子集的时间复杂度就是O(N^2)。具体编程思路采用嵌套两个循环的方式进行,外循环对应右指针,内循环对应左指针,外循环直接无条件遍历,内循环基于判断条件遍历,其实外循环存在隐藏条件,条件为内循环判断条件的对立面。最后就剩余一个问题,如何判断一个字符串是否存在于另一个字符串中,这里采用的是字典统计法,通过字典统一字符串中每个字符的出现频率,通过比较两个字典进行判断。
def minWindow(s, t):def check(dict1, dict2): # 定义一个函数检查dict2是否为dict1的子集for key, value in dict2.items():if dict1[key] < value:return Falsereturn Trueif len(s) < len(t): return ""key = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJGKLMNOPQRSTUVWXYZ" # 初始化两个字典,分别记录t和s前部分的字符分布dict1 = {} # 如果使用collections.Counter()效率关于更高dict2 = {}for i in range(len(key)):dict1[key[i]] = 0dict2[key[i]] = 0for i in range(len(t)):dict1[s[i]] += 1 # 得到s前len(t)的字符分布dict2[t[i]] += 1 # 得到t的字符分布if check(dict1, dict2): return s[0:len(t)] # 判断右指针为len(t)-1的起始情况min_len = len(s) + 1min_beign = 0min_end = 0left = 0 # 滑动窗口的左指针for right in range(len(t), len(s)): # 滑动窗口的右指针,从len(t)开始,隐藏条件:在dict2不是dict1子集的情况下移动右指针dict1[s[right]] += 1 # 每移动一个右指针必须马上修改其指纹dict1,对dict1的修改必须正在check函数之前while check(dict1, dict2): # 条件:在dict2是dict1子集的情况下移动左指针if min_len > right - left + 1: # 此时得到满足条件的子集min_len = right - left + 1min_beign = leftmin_end = rightdict1[s[left]] -= 1left += 1if min_end == 0:return ""else:return s[min_beign:min_end+1]5. 滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值 。
示例:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
该问题最朴素的想法就是固定窗口长度,向右滑动,直接找每个窗口的最大值即可,但是这样编程的时间复杂度不满足要求。本题需要借助大根堆这个完全二叉树结构(在 python 中 heapq 包对应的是小根堆,所以需要加入负号变大根堆)实现最大值的寻找,具体操作为起初用最左侧的的 k 个数值搭建一颗大根堆的完全二叉树,然后向右滑动窗口,每滑动一次,向大根堆增加一个数值,但此时的问题是如何删除滑动窗口最左侧剔除的数值,或者如何保证大根堆的最大值是在滑动窗口的当前范围内呢?其实这里不需要删除滑动窗口最左侧的值,只要保证大根堆的最大值永远落在滑动窗口内即可,具体操作就是使用 while 循环,在大根堆的最大值的索引不在滑动窗口范围内的情况下,持续将大根堆的主根剔除,在 while 循环终止后,大根堆的最大值一定落在滑动窗口的当前范围内,此时大根堆的最大值就是当前滑动窗口的最大值。此题的关键是想清楚,当滑动窗口右移时,没必要把滑动窗口左侧剔除的数据从大根堆中剔除。
import heapqdef maxSlidingWindow(nums, k):n = len(nums)# 注意 Python 默认的优先队列是小根堆q = [(-nums[i], i) for i in range(k)]heapq.heapify(q)ans = [-q[0][0]]for i in range(k, n):heapq.heappush(q, (-nums[i], i)) # 把新的字符放入大根堆while q[0][1] <= i - k: # 没必要把所有窗口外的数据踢走,只需要让找到的最大值在窗口范围内即可heapq.heappop(q)ans.append(-q[0][0])return ans相关文章:

leetcode滑动窗口问题总结 Python
目录 一、理论 二、例题 1. 最长无重复字符串 2. 长度最小的子数组 3. 字符串的排列 4. 最小覆盖子串 5. 滑动窗口最大值 一、理论 滑动窗口是一类比较重要的解题思路,一般来说我们面对的都是非定长窗口,所以一般需要定义两个指针 left 和 right&…...
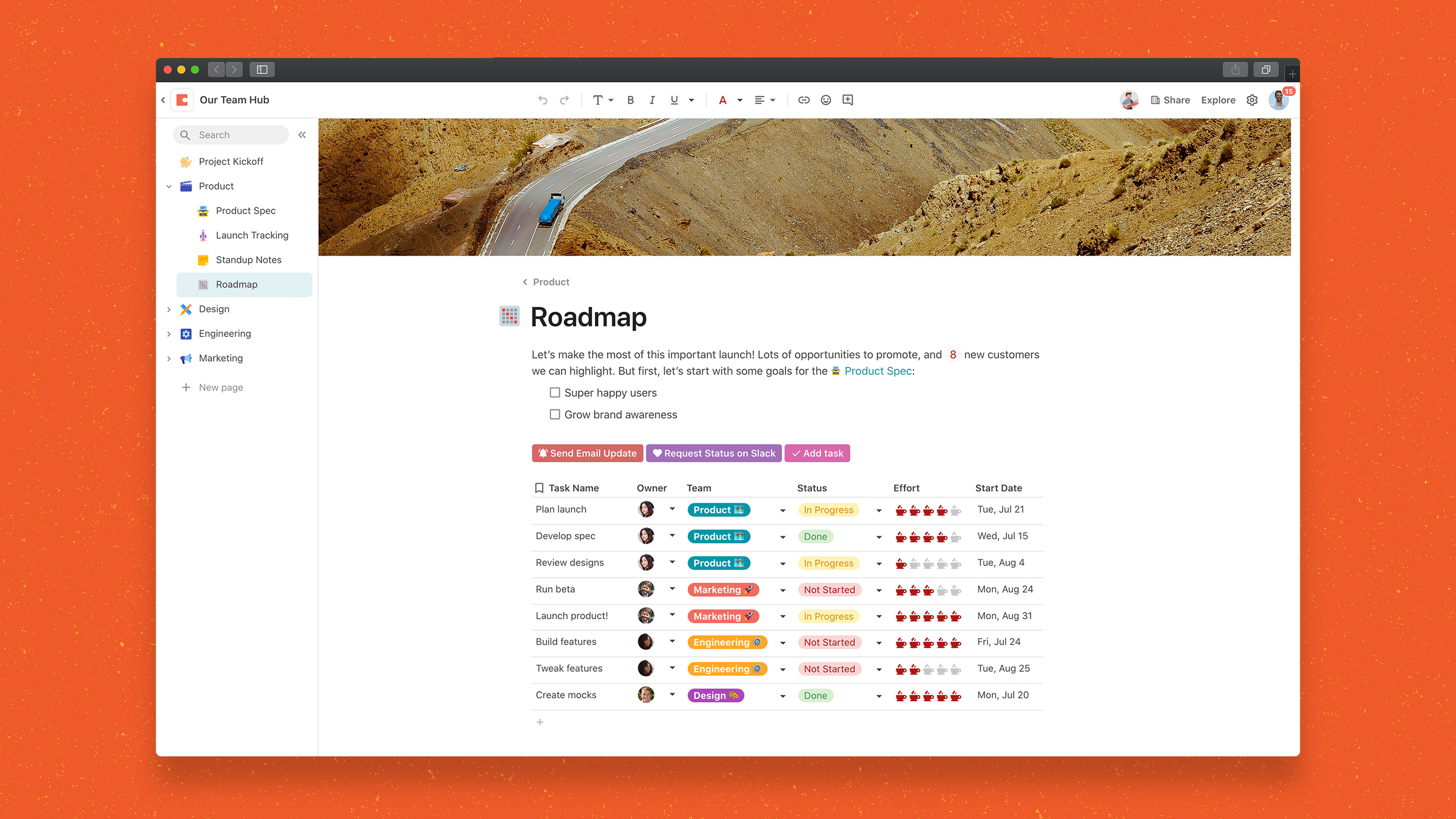
秒变办公达人,只因用了这5款在线协同文档app!
在日常工作中,我们不可避免地需要处理各种文档,有时你可能会为如何高效地管理这些文档而感到烦恼,或是不知道如何挑选合适的在线文档工具? 不用担心!在这篇文章中,我们将介绍5个好用的在线文档工具App&…...

镜头选型和计算
3.5 补充知识 一、单像元分辨率(单像素精度) 单像素精度是表示视觉系统综合精度的指标,表示一个像元对应检测目标的实际物理尺寸,是客户重点关注的 视觉系统参数; 计算公式1:单像素精度视野范围FOV/相机分辨…...
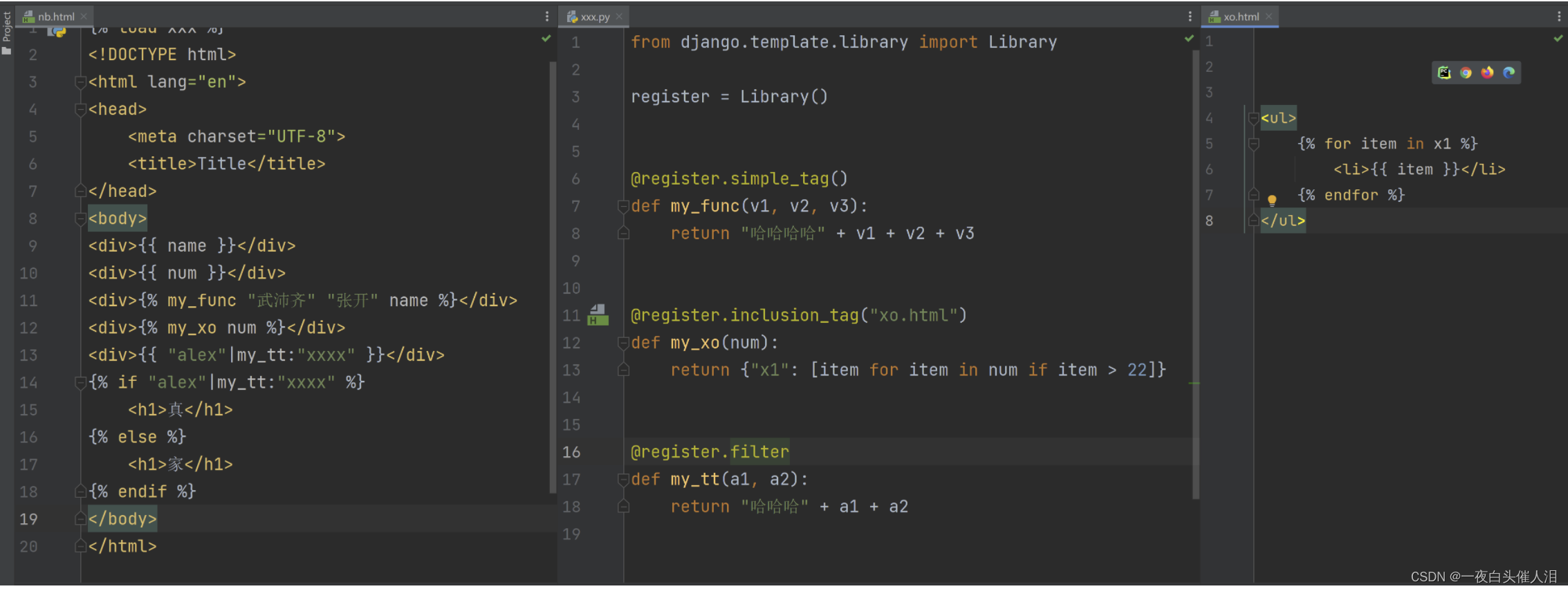
2024--Django平台开发-Django知识点(四)
1.知识回顾 创建项目:新项目、别人项目、新版版、老版本 项目目录(v1.0版本) 路由系统 常见路由编写加粗样式 /index/ 函数 /index/<str:v1> 函数 re_path(ryy/(\d{4})-(\d{2})-(\d{2})/, views.yy), re_path(ryy/(?…...

可狱可囚的爬虫系列课程 09:通过 API 接口抓取数据
前面已经讲解过 Requests 结合 BeautifulSoup4 库抓取数据,这种方式在抓取数据时还是比较方便快捷的,但是这并不意味着所有的网站都适合这种方式,并且这也不是抓取数据的最快方式,今天我们来讲一种更快速的获取数据的方式…...

2. Spring Boot 自动配置 Mybatis 流程
1. Spring Boot 自动配置 Mybatis 自动配置过程中做了3个主要bean的创建及很重要的一些事情。 sqlSessionFactory、sqlSessionTemplate、MapperScannerConfigurer 等配置bean的创建。sqlSessionFactory:解析 xml配置文件,并将MappedStatement放入到Has…...
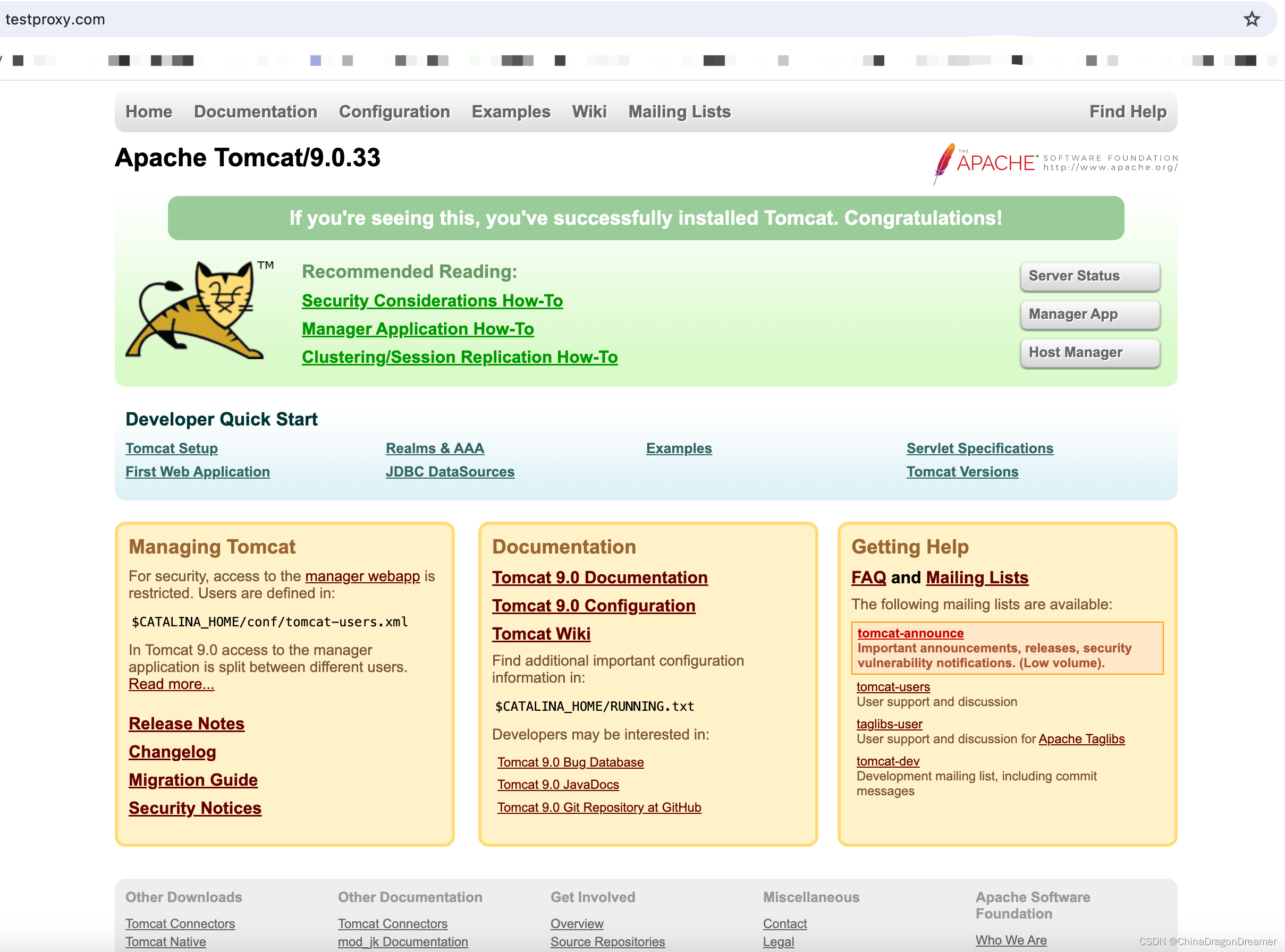
Nginx配置反向代理实例一
Mac 安装Nginx教程 提醒一下:下面实例讲解是在Mac系统演示的; 反向代理实例一实现的效果 在浏览器地址栏输入www.testproxy.com, 跳转到系统Tomcat主页面。 第一步:在系统的 hosts 文件进行ip和域名对应关系的配置。 Mac 系统修改Hosts文…...

训练自己的GPT2
训练自己的GPT2 1.预训练与微调2.准备工作2.在自己的数据上进行微调 1.预训练与微调 所谓的预训练,就是在海量的通用数据上训练大模型。比如,我把全世界所有的网页上的文本内容都整理出来,把全人类所有的书籍、论文都整理出来,然…...
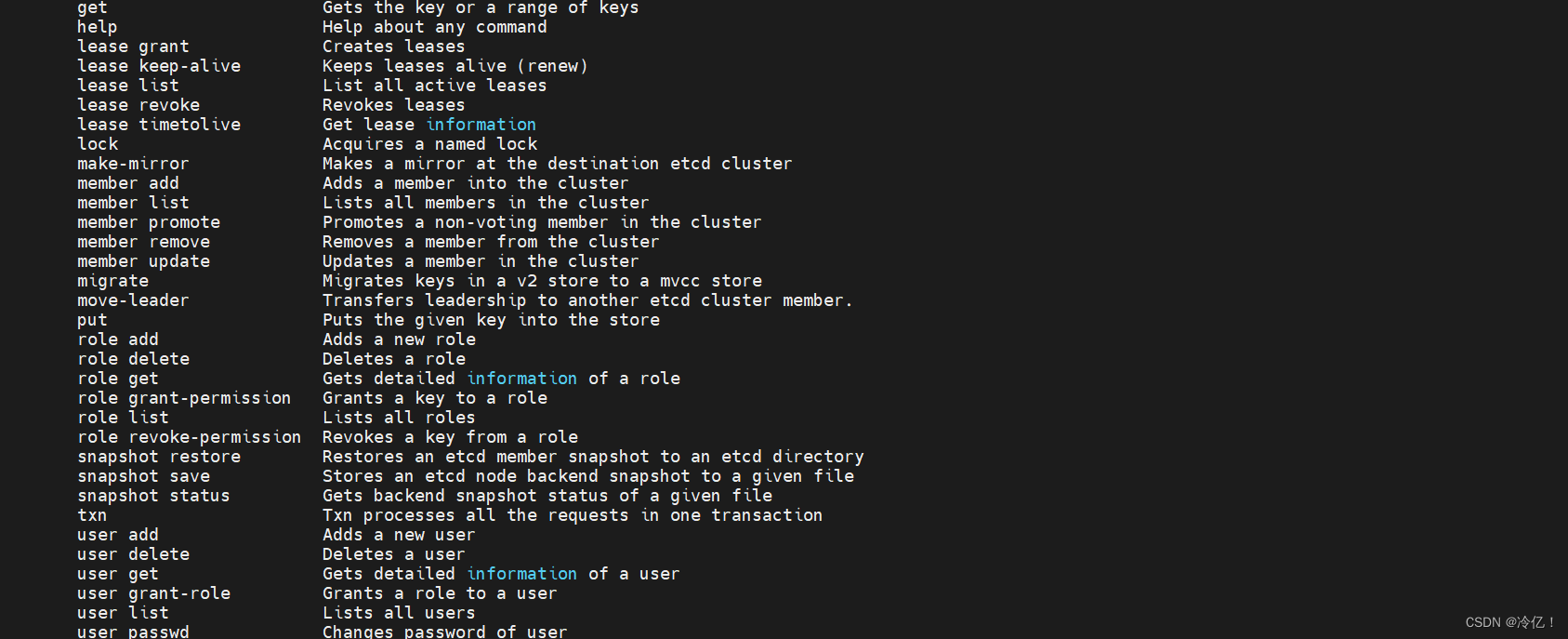
etcd储存安装
目录 etcd介绍: etcd工作原理 选举 复制日志 安全性 etcd工作场景 服务发现 etcd基本术语 etcd安装(centos) 设置:etcd后台运行 etcd 是云原生架构中重要的基础组件,由 CNCF 孵化托管。etcd 在微服务和 Kubernates 集群中不仅可以作为服务注册…...

如何彻底卸载Microsoft Edge浏览器
一、引语 随着微软推出全新的Edge浏览器,许多用户可能想要尝试或完全切换到其他浏览器。在这篇文章中,我们将向您介绍如何彻底卸载Microsoft Edge浏览器,以确保您的系统干净整洁。 二、通过系统设置卸载 1、首先,右键单击桌面上…...
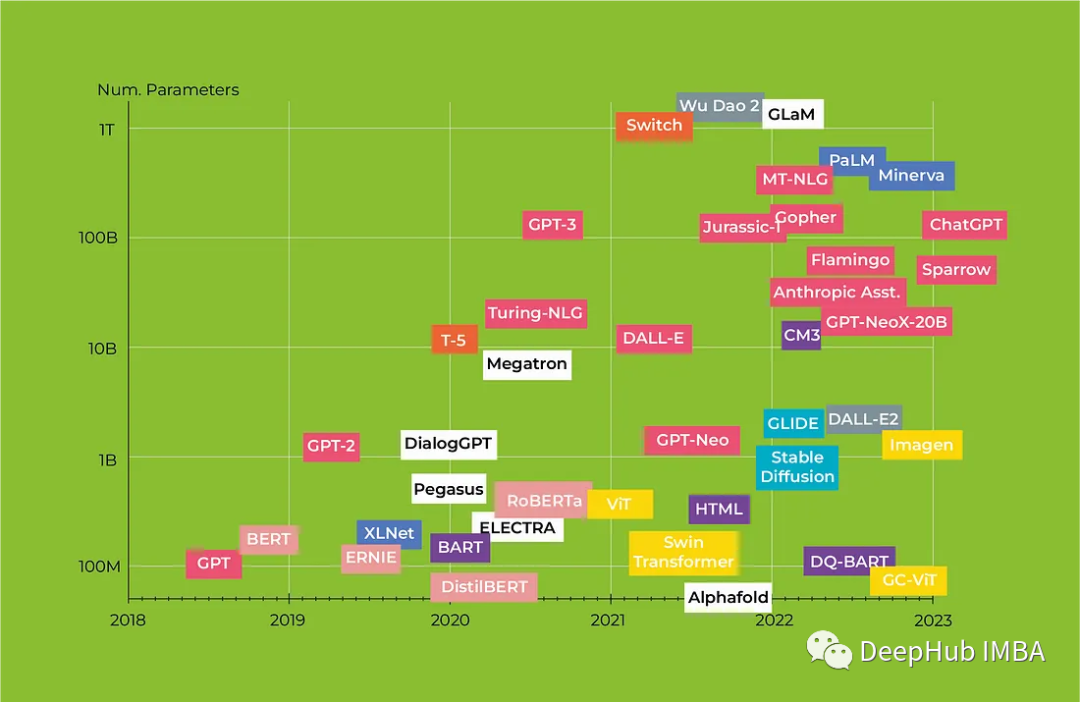
Transformers 2023年度回顾 :从BERT到GPT4
人工智能已成为近年来最受关注的话题之一,由于神经网络的发展,曾经被认为纯粹是科幻小说中的服务现在正在成为现实。从对话代理到媒体内容生成,人工智能正在改变我们与技术互动的方式。特别是机器学习 (ML) 模型在自然语言处理 (NLP) 领域取得…...

判断两个对象某些字段的值是否相同
1、借助mybatis plus的方法 import com.baomidou.mybatisplus.core.toolkit.LambdaUtils; import com.baomidou.mybatisplus.core.toolkit.support.SFunction; import com.baomidou.mybatisplus.core.toolkit.support.SerializedLambda; import lombok.SneakyThrows; import o…...

TYPE-C接口取电芯片介绍和应用场景
随着科技的发展,USB PDTYPE-C已经成为越来越多设备的充电接口。而在这一领域中,LDR6328Q PD取电芯片作为设备端协议IC芯片,扮演着至关重要的角色。本文将详细介绍LDR6328Q PD取电芯片的工作原理、应用场景以及选型要点。 一、工作原理 LDR63…...

基于TI TPSXX系列 Buck电路应用计算-外围器件详细计算过程
TPS54202 Buck电路应用计算 1、电气特性2、内部框图3、典型应用电路4、设计需求5、计算EN引脚电阻6、FB引脚电阻估算7、查看反馈电压电压基准8、输入电容计算10、FB引脚反馈电阻计算11、功率电感计算12、输出电容计算13、前馈电容计算15、Layout布局TPS54202-中文版 1、电气特…...
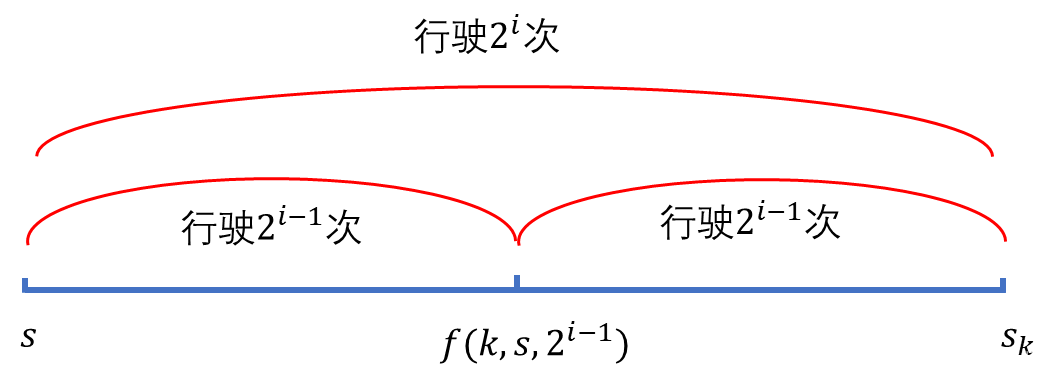
NOIP2012提高组day1-T3:开车旅行
题目链接 [NOIP2012 提高组] 开车旅行 题目描述 小 A \text{A} A 和小 B \text{B} B 决定利用假期外出旅行,他们将想去的城市从 1 1 1 到 n n n 编号,且编号较小的城市在编号较大的城市的西边,已知各个城市的海拔高度互不相同…...

Golang Web框架性能对比
Golang Web框架性能对比 github star排名依次: Gin Beego Iris Echo Revel Buffalo 性能上gin、iris、echo网上是给的数据都是五星,beego三星,revel两星 beego是国产,有中文文档,文档齐全 根据star数,性能,易用程度…...

【OCR】 - Tesseract OCR在mac系统中安装
Tesseract OCR 在Mac环境下安装Tesseract OCR(Optical Character Recognition)通常可以通过Homebrew包管理器进行。以下是安装步骤: 安装Homebrew 如果你还没有安装Homebrew,请访问 https://brew.sh/ 并按照页面上的说明安装。…...
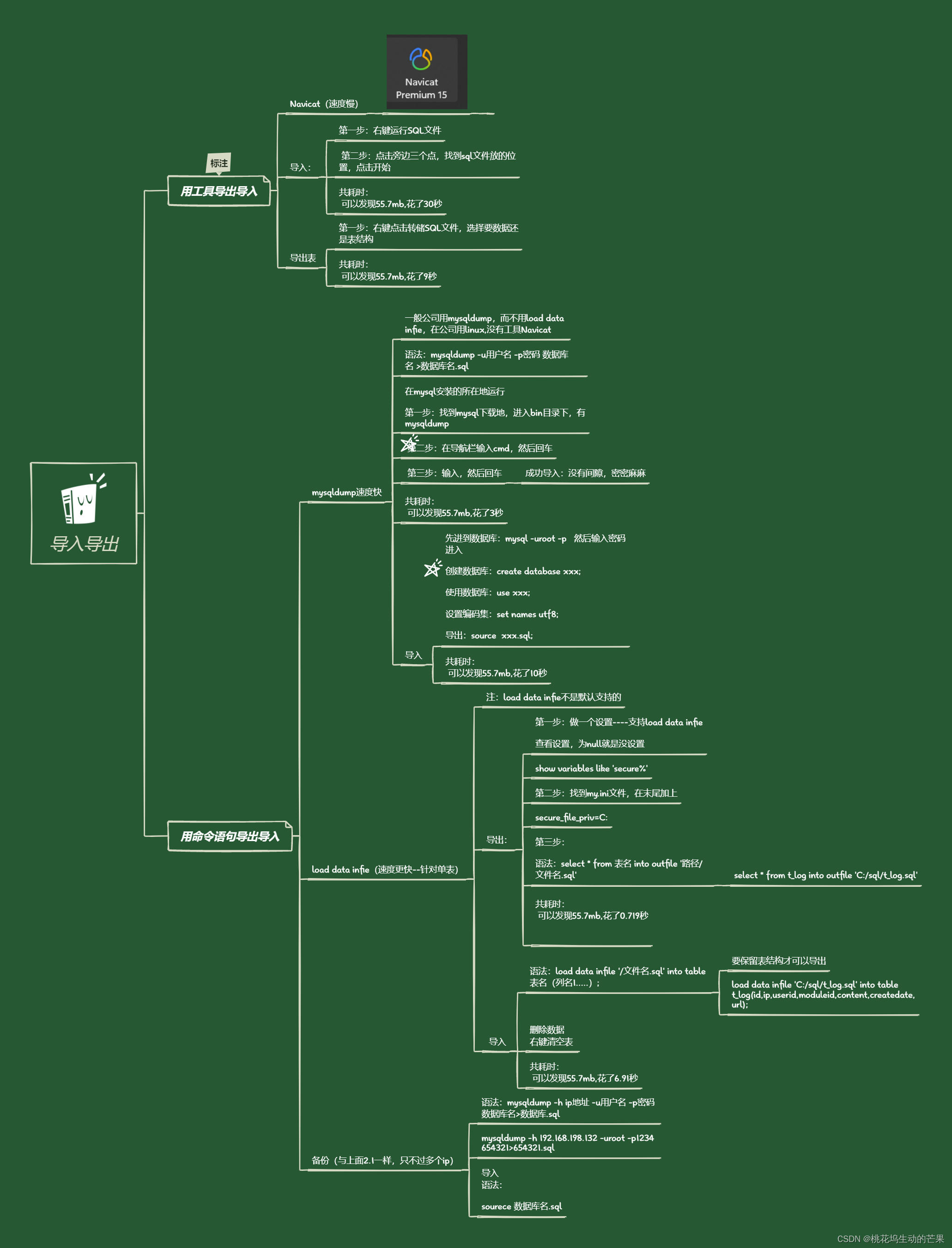
了解不同方式导入导出的速度之快
目录 一、用工具导出导入 Navicat(速度慢) 1.1、导入: 共耗时: 1.2、导出表 共耗时: 二、用命令语句导出导入 2.1、mysqldump速度快 导出表数据和表结构 共耗时: 只导出表结构 导入 共耗时&…...

2024年第九届计算机与通信系统国际会议(ICCCS2024) ,邀您相约西安!
会议官网: ICCCS2024 | Xian China 时间: 2024年4月19-22日 地点: 中国西安 会议简介: 近年来,信息通信在不断发展,为计算机网络的进步与发展提供了先进可靠的技术支持。随着计算机网络与通信技术的深入发展,计算机通信技术、数…...

获取直播间的最新评论 - python 取两个list的差集
python 取两个list的差集 作用:比如我要获取评论区列表,先获取了一遍,这个时候有人评论了几条,我再获取一遍后,找出多的那几条 使用set数据类型来取两个列表的差集。差集表示仅包含在第一个列表中而不在第二个列表中…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...
