Unity中URP下深度图的线性转化
文章目录
- 前言
- 一、_ZBufferParams参数有两组值
- 二、LinearEyeDepth
- 1、使用
- 2、Unity源码推导:
- 3、使用矩阵推导:
- 三、Linear01Depth
- 1、使用
- 2、Unity源码推导
- 3、数学推导:
前言
在之前的文章中,我们实现了对深度图的使用。因为,深度图不是线性的。所以,在使用时,我们使用了 Linear01Depth 函数对其进行了线性转化。
- Unity中URP下开启和使用深度图
但是,对深度图进行线性转化 还有其他函数。
在这篇文章中,我们来看一下深度图线性转化的 Linear01Depth函数 和 LinearEyeDepth 函数 干了什么。
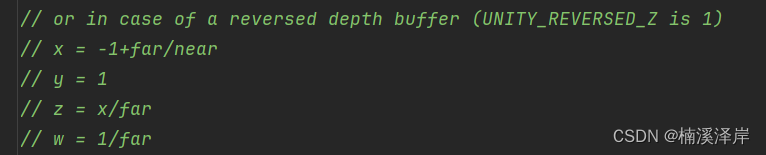
一、_ZBufferParams参数有两组值
-
在OpenGL下

-
在类DirectX下
二、LinearEyeDepth
1、使用
-
对采样的深度图纹理进行线性转化
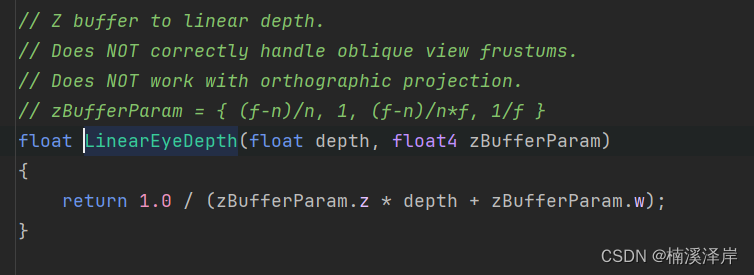
-
转化后的值,就是原来物体的深度 Z 值
float4 cameraDepthTex = SAMPLE_TEXTURE2D(_CameraDepthTexture,sampler_CameraDepthTexture,uv);
float depthTex = LinearEyeDepth(cameraDepthTex,_ZBufferParams);
- 返回结果全白,效果不明显

- 我们对其取小数部分,使其效果明显一点
frac(depthTex)

2、Unity源码推导:
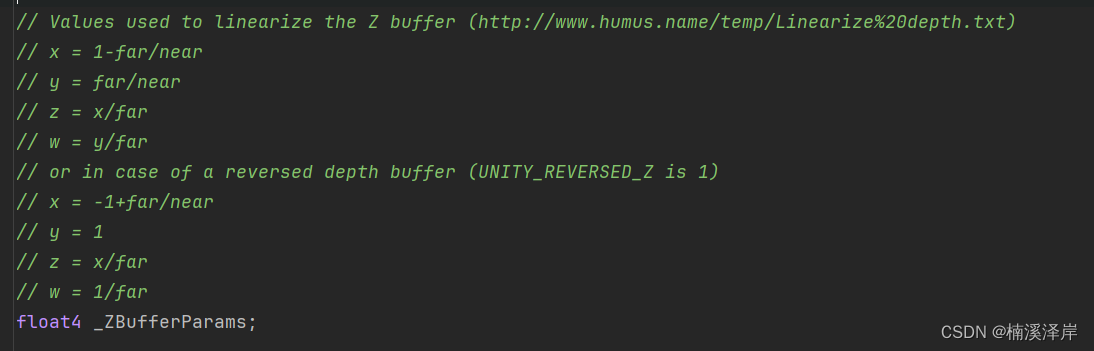
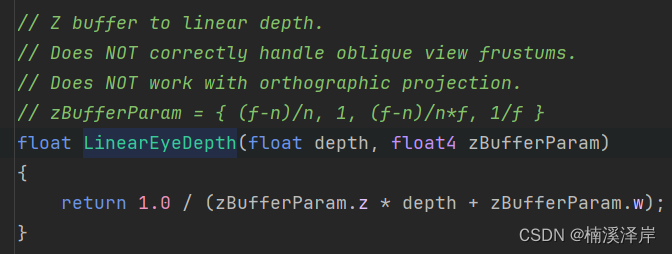
- 这里使用OpenGL下推导
Z v i e w = 1 1 − f n f d + f n f Z_{view}=\frac{1}{\frac{1-\frac{f}{n}}{f}d+\frac{\frac{f}{n}}{f}} Zview=f1−nfd+fnf1
Z v i e w = 1 ( n n − f n ) 1 f d + 1 n Z_{view}=\frac{1}{(\frac{n}{n}-\frac{f}{n})\frac{1}{f}d+\frac{1}{n}} Zview=(nn−nf)f1d+n11
Z v i e w = 1 ( n − f n ) 1 f d + 1 n Z_{view}=\frac{1}{(\frac{n-f}{n})\frac{1}{f}d+\frac{1}{n}} Zview=(nn−f)f1d+n11
Z v i e w = 1 n − f n f d + 1 n Z_{view}=\frac{1}{\frac{n-f}{nf}d+\frac{1}{n}} Zview=nfn−fd+n11
3、使用矩阵推导:
-
OpenGL
[ 2 n w 0 0 0 0 2 n h 0 0 0 0 n + f n − f 2 n f n − f 0 0 − 1 0 ] \begin{bmatrix} \frac{2n}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & \frac{n+f}{n-f} &\frac{2nf}{n-f}\\ 0 & 0 & -1 & 0\\ \end{bmatrix} w2n0000h2n0000n−fn+f−100n−f2nf0 -
DirectX
[ 2 n w 0 0 0 0 2 n h 0 0 0 0 n f − n n f f − n 0 0 − 1 0 ] \begin{bmatrix} \frac{2n}{w} & 0 & 0 & 0 \\ 0 & \frac{2n}{h} & 0 &0\\ 0 & 0 & \frac{n}{f-n} &\frac{nf}{f-n}\\ 0 & 0 & -1 & 0\\ \end{bmatrix} w2n0000h2n0000f−nn−100f−nnf0 -
由观察空间转化到裁剪空间矩阵可得
Z c l i p = n + f n − f Z v i e w + 2 n f n − f W v i e w Z_{clip}=\frac{n+f}{n-f}Z_{view}+\frac{2nf}{n-f}W_{view} Zclip=n−fn+fZview+n−f2nfWview
W c l i p = − Z v i e w W_{clip}=-Z_{view} Wclip=−Zview -
做透视除法可得
Z n d c = Z c l i p W c l i p = n + f n − f Z v i e w + 2 n f n − f − Z v i e w = n + f f − n + 2 n f ( f − n ) Z v i e w Z_{ndc} = \frac{Z_{clip}}{W_{clip}} = \frac{\frac{n+f}{n-f}Z_{view}+\frac{2nf}{n-f}}{-Z_{view}}=\frac{n+f}{f-n}+\frac{2nf}{(f-n)Z_{view}} Zndc=WclipZclip=−Zviewn−fn+fZview+n−f2nf=f−nn+f+(f−n)Zview2nf -
d = 0.5 ⋅ Z n d c + 0.5 d=0.5·Z_{ndc}+0.5 d=0.5⋅Zndc+0.5
d = 0.5 ⋅ ( n + f f − n + 2 n f ( f − n ) Z v i e w ) + 0.5 d = 0.5·(\frac{n+f}{f-n}+\frac{2nf}{(f-n)Z_{view}})+0.5 d=0.5⋅(f−nn+f+(f−n)Zview2nf)+0.5 -
我们由 d d d 公式化简,即可得到 Z v i e w Z_{view} Zview
Z v i e w = 1 f − n n f d − 1 n Z_{view} = \frac{1}{\frac{f-n}{nf}d-\frac{1}{n}} Zview=nff−nd−n11 -
为了得到正的Z值,需要取反
Z v i e w = − 1 f − n n f d − 1 n Z_{view} =- \frac{1}{\frac{f-n}{nf}d-\frac{1}{n}} Zview=−nff−nd−n11
Z v i e w = 1 n − f n f d + 1 n Z_{view}=\frac{1}{\frac{n-f}{nf}d+\frac{1}{n}} Zview=nfn−fd+n11
三、Linear01Depth
1、使用
-
对采样的深度图纹理进行线性转化
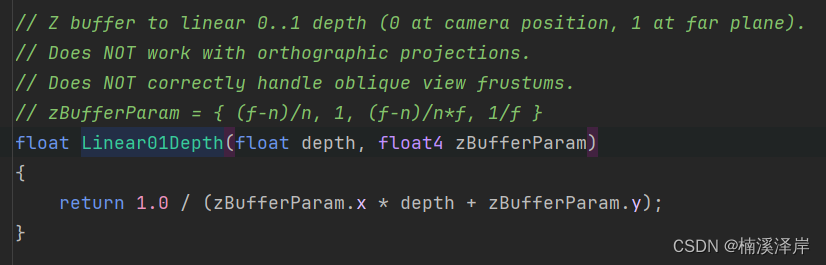
-
转化后的值,是Z值在[0,1]区间的值
float4 cameraDepthTex = SAMPLE_TEXTURE2D(_CameraDepthTexture,sampler_CameraDepthTexture,uv);
float depthTex = Linear01Depth(cameraDepthTex,_ZBufferParams);
- 返回结果

2、Unity源码推导
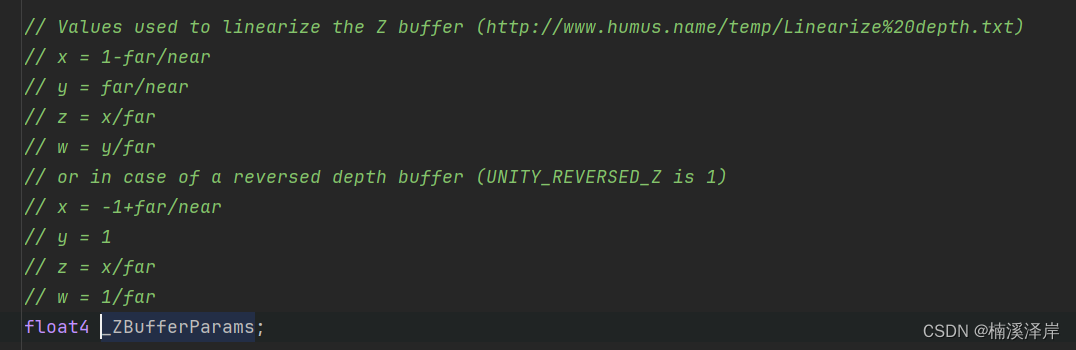
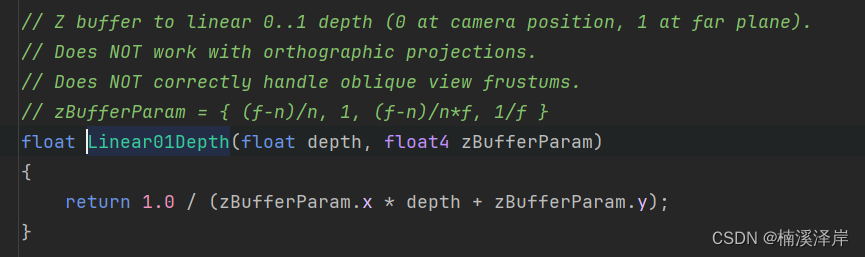
- OpenGL下推导:
Z v i e w = 1 ( 1 − f n ) d + f n Z_{view}= \frac{1}{(1-\frac{f}{n})d+\frac{f}{n}} Zview=(1−nf)d+nf1
3、数学推导:
-
这是LinearEyeDepth下推导出来的
Z v i e w = 1 n − f n f d + 1 n Z_{view}=\frac{1}{\frac{n-f}{nf}d+\frac{1}{n}} Zview=nfn−fd+n11 -
Z v i e w Z_{view} Zview的取值范围 [ n e a r , f a r ] [near,far] [near,far]
-
使其除以一个 f f f得到 Linear01Depth函数的结果
Z v i e w = 1 n − f n f d + 1 n ⋅ 1 f = 1 n − f n f d f + f n = 1 ( 1 − f n ) d + f n Z_{view}=\frac{1}{\frac{n-f}{nf}d+\frac{1}{n}}·\frac{1}{f}=\frac{1}{\frac{n-f}{nf}df+\frac{f}{n}}=\frac{1}{(1-\frac{f}{n})d+\frac{f}{n}} Zview=nfn−fd+n11⋅f1=nfn−fdf+nf1=(1−nf)d+nf1
相关文章:

Unity中URP下深度图的线性转化
文章目录 前言一、_ZBufferParams参数有两组值二、LinearEyeDepth1、使用2、Unity源码推导:3、使用矩阵推导: 三、Linear01Depth1、使用2、Unity源码推导3、数学推导: 前言 在之前的文章中,我们实现了对深度图的使用。因为&#…...

Low Poly Cartoon House Interiors
400个独特的低多边形预制件的集合,可以轻松创建高质量的室内场景。所有模型都已准备好放入场景中,并使用一个纹理创建,以提高性能!包含演示场景! 模型分类: - 墙壁(79件) - 地板(28块) - 浴室(33个) - 厨房(36件) - 厨房道具(68件) - 房间道具(85件) - 灯具(…...
)
[算法与数据结构][c++]:左值、右值、左值引用、右值引用和std::move()
左值、右值、左值引用、右值引用和std::move 1. 什么是左值、右值2. 什么是左值引用、右值引用3. **右值引用和std::move的应用场景**3.1 实现移动语义3.2 **实例:vector::push_back使用std::move提高性能** **4. 完美转发 std::forward**5. Reference 写在前面&…...

【QT】day3
1.登陆界面 2.登陆失败 3.登陆成功弹窗 4.点击OK后跳转 #include "mainwindow.h" #include "ui_mainwindow.h"MainWindow::MainWindow(QWidget *parent): QMainWindow(parent), ui(new Ui::MainWindow) {ui->setupUi(this); }MainWindow::~MainWindow…...

c++ fork, execl 参数 logcat | grep
Linux进程编程(PS: exec族函数、system、popen函数)_linux popen函数会新建进程吗-CSDN博客 execvp函数详解_如何在C / C 中使用execvp()函数-CSDN博客 C语言的多进程fork()、函数exec*()、system()与popen()函数_c语言 多进程-CSDN博客 Linux---fork…...
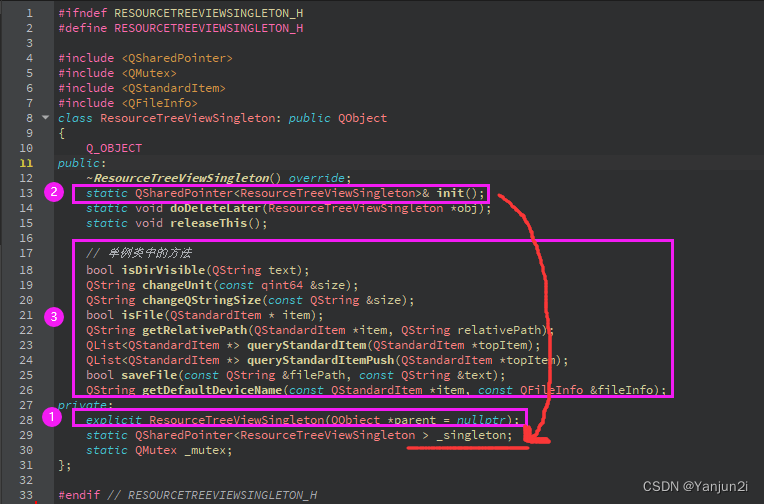
QT:单例
单例的定义 官方定义:单例是指确保一个类在任何情况下都绝对只有一个实例,并提供一个全局访问点。 单例的写法 抓住3点: 构造函数私有化(确保只有一个实例)提供一个可以获取构造实例的接口(提供唯一的实…...

IPv6路由协议---IPv6动态路由(OSPFv3-4)
OSPFv3的链路状态通告LSA类型 链路状态通告是OSPFv3进行路由计算的关键依据,链路状态通告包含链路状态类型、链路状态ID、通告路由器三元组唯一地标识了一个LSA。 OSPFv3的LSA头仍然保持20字节,但是内容变化了。在LSA头中,OSPFv2的LS age、Advertising Router、LS Sequence…...
移动通信原理与关键技术学习(4)
1.小尺度衰落 Small-Scale Fading 由于收到的信号是由通过不同的多径到达的信号的总和,接收信号的增强有一定的减小。 小尺度衰落的特点: 信号强度在很小的传播距离或时间间隔内的快速变化;不同多径信号多普勒频移引起的随机调频ÿ…...

第二百五十八回
文章目录 1. 概念介绍2. 思路与方法2.1 实现思路2.2 实现方法 3. 示例代码4. 内容总结 我们在上一章回中介绍了"模拟对话窗口的页面"相关的内容,本章回中将介绍如何创建一个可以输入内容的对话框.闲话休提,让我们一起Talk Flutter吧。 1. 概念…...

freesurfer-reconall后批量提取TIV(颅内总体积)
#提取TIV #singleline=$(grep Estimated Total Intracranial Volume /usr/local/freesurfer/subjects/bect-3d+bold-wangjingchen-4.9y-2/stats/aseg.sta...

【GO】如何用 Golang 的 os/exec 执行 pipe 替换文件
背景 主要记录一下怎么用 Golang 的 os/exec 去执行一个 cmd 的 pipeline,就是拿 cmdA 的输出作为 cmdB 的输入,这里记录了两种方法去替换文件里面的字符串。 pipe 那个逻辑在 demo1 里。 另外一种是直接读文件做替换,一不小心两个都放进来了…...
基于Spring-boot-websocket的聊天应用开发总结
目录 1.概述 1.1 Websocket 1.2 STOMP 1.3 源码 2.Springboot集成WS 2.1 添加依赖 2.2 ws配置 2.2.1 WebSocketMessageBrokerConfigurer 2.2.2 ChatController 2.2.3 ChatInRoomController 2.2.4 ChatToUserController 2.3 前端聊天配置 2.3.1 index.html和main.j…...

2023年度总结 - 职业生涯第一个十年
2023年只剩下最后一周,又到了一年一度该做年末总结的时候了。 回想起去年,还有人专门建立了一个关于年度总结文章汇总的仓库。读了很多篇别人写的,给了我很多的触动和感想。这里的每篇文章都是关于某个人这一整年的生活和工作的轨迹啊。即使你…...
setup 语法糖
只有vue3.2以上版本可以使用 优点: 更少的样板内容,更简洁的代码 能够使用纯 Typescript 声明props 和抛出事件 更好的运行时性能 更好的IDE类型推断性能 在sciprt标识上加上setup 顶层绑定都可以使用 不需要return ,可以直接使用 使用组件…...
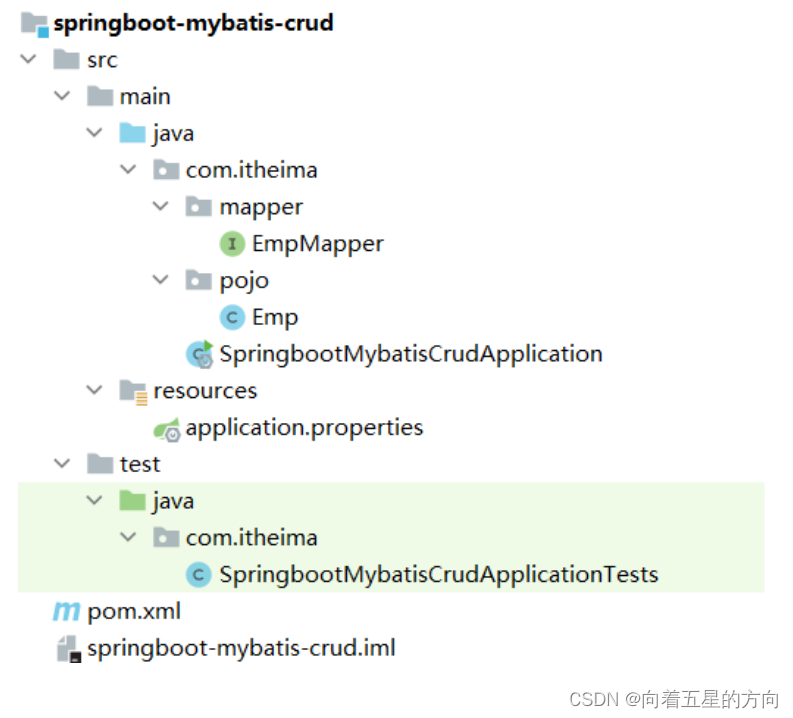
Javaweb之Mybatis的基础操作的详细解析
1. Mybatis基础操作 学习完mybatis入门后,我们继续学习mybatis基础操作。 1.1 需求 需求说明 通过分析以上的页面原型和需求,我们确定了功能列表: 查询 根据主键ID查询 条件查询 新增 更新 删除 根据主键ID删除 根据主键ID批量删除 …...

知名开发者社区Stack Overflow发布《2023 年开发者调查报告》
Stack Overflow成立于2008年,最知名的是它的公共问答平台,每月有超过 1 亿人访问该平台来提问、学习和分享技术知识。是世界上最受欢迎的开发者社区之一。每年都会发布一份关于开发者的调查报告,来了解不断变化的开发人员现状、正在兴起或衰落…...

vue element plus Form 表单
表单包含 输入框, 单选框, 下拉选择, 多选框 等用户输入的组件。 使用表单,您可以收集、验证和提交数据。 TIP Form 组件已经从 2. x 的 Float 布局升级为 Flex 布局。 典型表单# 最基础的表单包括各种输入表单项,比如input、select、radio、checkbo…...

zmq_connect和zmq_poll
文章内容: 介绍函数zmq_connect和zmq_poll的使用 zmq_connect zmq_connect函数是ZeroMQ库中的一个函数,用于在C语言中创建一个与指定地址的ZeroMQ套接字的连接。该函数的原型如下: int zmq_connect(void *socket, const char *endpoint);其…...
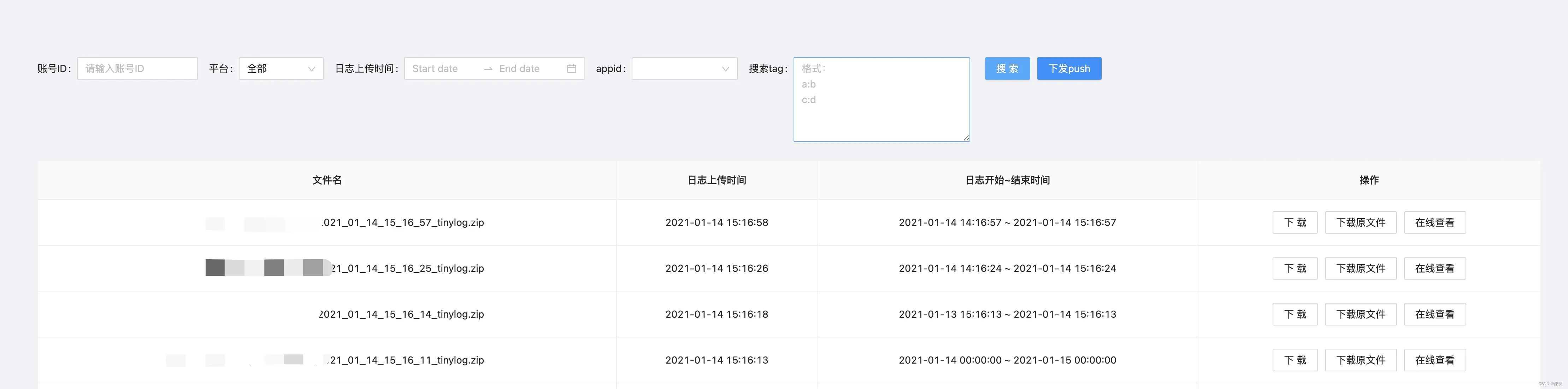
TinyLog iOS v3.0接入文档
1.背景 为在线教育部提供高效、安全、易用的日志组件。 2.功能介绍 2.1 日志格式化 目前输出的日志格式如下: 日志级别/[YYYY-MM-DD HH:MM:SS MS] TinyLog-Tag: |线程| 代码文件名:行数|函数名|日志输出内容触发flush到文件的时机: 每15分钟定时触发…...

react-native 配置@符号绝对路径配置和绝对路径没有提示的问题
这里需要用到vscode的包 yarn add babel-plugin-module-resolver 找到根目录里的babel.config.js 在页面添加plugins配置 直接替换 module.exports {presets: [module:metro-react-native-babel-preset],plugins: [[module-resolver,{root: [./src],alias: {/utils: ./src/…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
