[足式机器人]Part2 Dr. CAN学习笔记 - Ch03 傅里叶级数与变换
本文仅供学习使用
本文参考:
B站:DR_CAN
Dr. CAN学习笔记-Ch03 傅里叶级数与变换
- 1. 三角函数的正交性
- 2. 周期为 2 π 2\pi 2π的函数展开为傅里叶级数
- 3. 周期为 2 L 2L 2L的函数展开
- 4. 傅里叶级数的复数形式
- 5. 从傅里叶级数推导傅里叶变换FT
- 6. 总结
1. 三角函数的正交性
三角函数系 : 集合 { sin n x , cos n x } n = 0 , 1 , 2 , ⋯ \left\{ \sin nx,\cos nx \right\} n=0,1,2,\cdots {sinnx,cosnx}n=0,1,2,⋯
正交:
∫ − π π sin n x sin m x d x = 0 , n ≠ m ∫ − π π sin n x cos m x d x = 0 , n ≠ m ∫ − π π cos n x sin m x d x = 0 , n ≠ m \int_{-\pi}^{\pi}{\sin nx\sin mx}\mathrm{d}x=0,n\ne m \\ \int_{-\pi}^{\pi}{\sin nx\cos mx}\mathrm{d}x=0,n\ne m \\ \int_{-\pi}^{\pi}{\cos nx\sin mx}\mathrm{d}x=0,n\ne m ∫−ππsinnxsinmxdx=0,n=m∫−ππsinnxcosmxdx=0,n=m∫−ππcosnxsinmxdx=0,n=m
积化和差: ⇒ ∫ − π π 1 2 [ cos ( n − m ) x + cos ( n + m ) x ] d x = 1 2 1 ( n − m ) sin ( n − m ) x ∣ − π π + 1 2 1 ( n + m ) sin ( n + m ) x ∣ − π π \Rightarrow \int_{-\pi}^{\pi}{\frac{1}{2}\left[ \cos \left( n-m \right) x+\cos \left( n+m \right) x \right]}\mathrm{d}x=\frac{1}{2}\frac{1}{\left( n-m \right)}\sin \left( n-m \right) x\mid_{-\pi}^{\pi}+\frac{1}{2}\frac{1}{\left( n+m \right)}\sin \left( n+m \right) x\mid_{-\pi}^{\pi} ⇒∫−ππ21[cos(n−m)x+cos(n+m)x]dx=21(n−m)1sin(n−m)x∣−ππ+21(n+m)1sin(n+m)x∣−ππ
∫ − π π cos m x cos m x d x = π \int_{-\pi}^{\pi}{\cos mx\cos mx}\mathrm{d}x=\pi ∫−ππcosmxcosmxdx=π
2. 周期为 2 π 2\pi 2π的函数展开为傅里叶级数
T = 2 π : f ( x ) = f ( x + 2 π ) T=2\pi :f\left( x \right) =f\left( x+2\pi \right) T=2π:f(x)=f(x+2π)
f ( x ) = ∑ n = 0 ∞ a n cos n x + ∑ n = 0 ∞ b n sin n x = a 0 cos o x + ∑ n = 1 ∞ a n cos n x + b 0 sin 0 x + ∑ n = 1 ∞ b n sin n x = a 0 + ∑ n = 1 ∞ a n cos n x + ∑ n = 1 ∞ b n sin n x f\left( x \right) =\sum_{n=0}^{\infty}{a_{\mathrm{n}}\cos nx}+\sum_{n=0}^{\infty}{b_{\mathrm{n}}\sin nx}=a_0\cos ox+\sum_{n=1}^{\infty}{a_{\mathrm{n}}\cos nx}+b_0\sin 0x+\sum_{n=1}^{\infty}{b_{\mathrm{n}}\sin nx}=a_0+\sum_{n=1}^{\infty}{a_{\mathrm{n}}\cos nx}+\sum_{n=1}^{\infty}{b_{\mathrm{n}}\sin nx} f(x)=n=0∑∞ancosnx+n=0∑∞bnsinnx=a0cosox+n=1∑∞ancosnx+b0sin0x+n=1∑∞bnsinnx=a0+n=1∑∞ancosnx+n=1∑∞bnsinnx
- 找 a 0 a_0 a0:
∫ − π π f ( x ) d x = ∫ − π π a 0 d x + ∫ − π π 1 ⋅ ∑ n = 1 ∞ a n cos n x d x + ∫ − π π 1 ⋅ ∑ n = 1 ∞ b n sin n x d x = a 0 ∫ − π π d x + 0 + 0 = a 0 ⋅ 2 π \int_{-\pi}^{\pi}{f\left( x \right)}\mathrm{d}x=\int_{-\pi}^{\pi}{a_0}\mathrm{d}x+\int_{-\pi}^{\pi}{1\cdot \sum_{n=1}^{\infty}{a_{\mathrm{n}}\cos nx}}\mathrm{d}x+\int_{-\pi}^{\pi}{1\cdot \sum_{n=1}^{\infty}{b_{\mathrm{n}}\sin nx}}\mathrm{d}x \\ =a_0\int_{-\pi}^{\pi}{}\mathrm{d}x+0+0=a_0\cdot 2\pi ∫−ππf(x)dx=∫−ππa0dx+∫−ππ1⋅n=1∑∞ancosnxdx+∫−ππ1⋅n=1∑∞bnsinnxdx=a0∫−ππdx+0+0=a0⋅2π
⇒ a 0 = 1 2 π ∫ − π π f ( x ) d x \Rightarrow a_0=\frac{1}{2\pi}\int_{-\pi}^{\pi}{f\left( x \right)}\mathrm{d}x ⇒a0=2π1∫−ππf(x)dx - 找 a n a_n an:
∫ − π π f ( x ) cos m x d x = ∫ − π π a 0 cos m x ⋅ 1 d x + ∫ − π π ∑ n = 1 ∞ a n cos n x cos m x d x + ∫ − π π ∑ n = 1 ∞ b n sin n x cos m x d x = ∫ − π π a n cos n x cos n x d x = a n π \int_{-\pi}^{\pi}{f\left( x \right) \cos mx}\mathrm{d}x=\int_{-\pi}^{\pi}{a_0}\cos mx\cdot 1\mathrm{d}x+\int_{-\pi}^{\pi}{\sum_{n=1}^{\infty}{a_{\mathrm{n}}\cos nx\cos mx}}\mathrm{d}x+\int_{-\pi}^{\pi}{\sum_{n=1}^{\infty}{b_{\mathrm{n}}\sin nx\cos mx}}\mathrm{d}x=\int_{-\pi}^{\pi}{a_{\mathrm{n}}\cos nx\cos nx}\mathrm{d}x=a_{\mathrm{n}}\pi ∫−ππf(x)cosmxdx=∫−ππa0cosmx⋅1dx+∫−ππn=1∑∞ancosnxcosmxdx+∫−ππn=1∑∞bnsinnxcosmxdx=∫−ππancosnxcosnxdx=anπ
⇒ a n = 1 π ∫ − π π f ( x ) cos n x d x \Rightarrow a_{\mathrm{n}}=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \cos nx}\mathrm{d}x ⇒an=π1∫−ππf(x)cosnxdx - 找 b n b_n bn:
∫ − π π f ( x ) sin . m x d x ⇒ b n = 1 π ∫ − π π f ( x ) sin n x d x \int_{-\pi}^{\pi}{f\left( x \right) \sin .mx}\mathrm{d}x\Rightarrow b_{\mathrm{n}}=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \sin nx}\mathrm{d}x ∫−ππf(x)sin.mxdx⇒bn=π1∫−ππf(x)sinnxdx
⇒ f ( x ) = f ( x + 2 π ) , T = 2 π { f ( x ) = a 0 2 + ∑ n = 0 ∞ a n cos n x + ∑ n = 0 ∞ b n sin n x a 0 = 1 2 π ∫ − π π f ( x ) d x a n = 1 π ∫ − π π f ( x ) cos n x d x b n = 1 π ∫ − π π f ( x ) sin n x d x \Rightarrow f\left( x \right) =f\left( x+2\pi \right) ,T=2\pi \begin{cases} f\left( x \right) =\frac{a_0}{2}+\sum_{n=0}^{\infty}{a_{\mathrm{n}}\cos nx}+\sum_{n=0}^{\infty}{b_{\mathrm{n}}\sin nx}\\ a_0=\frac{1}{2\pi}\int_{-\pi}^{\pi}{f\left( x \right)}\mathrm{d}x\\ a_{\mathrm{n}}=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \cos nx}\mathrm{d}x\\ b_{\mathrm{n}}=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \sin nx}\mathrm{d}x\\ \end{cases} ⇒f(x)=f(x+2π),T=2π⎩ ⎨ ⎧f(x)=2a0+∑n=0∞ancosnx+∑n=0∞bnsinnxa0=2π1∫−ππf(x)dxan=π1∫−ππf(x)cosnxdxbn=π1∫−ππf(x)sinnxdx
3. 周期为 2 L 2L 2L的函数展开
f ( t ) = f ( t + 2 L ) f\left( t \right) =f\left( t+2L \right) f(t)=f(t+2L) , 换元: x = π L t , t = L π x x=\frac{\pi}{L}t,t=\frac{L}{\pi}x x=Lπt,t=πLx
f ( t ) = f ( L π x ) = g ( x ) , g ( x + 2 π ) = f ( L π ( x + 2 π ) ) = f ( L π x + 2 L ) = f ( L π x ) = g ( x ) f\left( t \right) =f\left( \frac{L}{\pi}x \right) =g\left( x \right) ,g\left( x+2\pi \right) =f\left( \frac{L}{\pi}\left( x+2\pi \right) \right) =f\left( \frac{L}{\pi}x+2L \right) =f\left( \frac{L}{\pi}x \right) =g\left( x \right) f(t)=f(πLx)=g(x),g(x+2π)=f(πL(x+2π))=f(πLx+2L)=f(πLx)=g(x)
g ( x ) = a 0 2 + ∑ n = 1 ∞ [ a n cos n x + b n sin n x ] a 0 = 1 2 π ∫ − π π f ( x ) d x , a n = 1 π ∫ − π π f ( x ) cos n x d x , b n = 1 π ∫ − π π f ( x ) sin n x d x g\left( x \right) =\frac{a_0}{2}+\sum_{n=1}^{\infty}{\left[ a_{\mathrm{n}}\cos nx+b_{\mathrm{n}}\sin nx \right]} \\ a_0=\frac{1}{2\pi}\int_{-\pi}^{\pi}{f\left( x \right)}\mathrm{d}x,a_{\mathrm{n}}=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \cos nx}\mathrm{d}x,b_{\mathrm{n}}=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \sin nx}\mathrm{d}x g(x)=2a0+n=1∑∞[ancosnx+bnsinnx]a0=2π1∫−ππf(x)dx,an=π1∫−ππf(x)cosnxdx,bn=π1∫−ππf(x)sinnxdx
→ x = π L t ⇒ cos n x = cos n π L t , sin n x = sin n π L t , g ( x ) = f ( t ) ∫ − π π d x = ∫ − π π d π L t ⇒ 1 π ∫ − π π d x = 1 L ∫ − L L d t \rightarrow x=\frac{\pi}{L}t\Rightarrow \cos nx=\cos \frac{n\pi}{L}t,\sin nx=\sin \frac{n\pi}{L}t,g\left( x \right) =f\left( t \right) \\ \int_{-\pi}^{\pi}{}\mathrm{d}x=\int_{-\pi}^{\pi}{}\mathrm{d}\frac{\pi}{L}t\Rightarrow \frac{1}{\pi}\int_{-\pi}^{\pi}{}\mathrm{d}x=\frac{1}{L}\int_{-L}^L{}\mathrm{d}t →x=Lπt⇒cosnx=cosLnπt,sinnx=sinLnπt,g(x)=f(t)∫−ππdx=∫−ππdLπt⇒π1∫−ππdx=L1∫−LLdt
⇒ f ( t ) = a 0 2 + ∑ n = 1 ∞ [ a n cos n π L t + b n sin n π L t ] , a 0 = 1 L ∫ − L L f ( t ) d t , a n = 1 L ∫ − L L f ( t ) cos n π L t d t , b n = 1 L ∫ − L L f ( t ) sin n π L t d t \Rightarrow f\left( t \right) =\frac{a_0}{2}+\sum_{n=1}^{\infty}{\left[ a_{\mathrm{n}}\cos \frac{n\pi}{L}t+b_{\mathrm{n}}\sin \frac{n\pi}{L}t \right]},a_0=\frac{1}{L}\int_{-L}^L{f\left( t \right)}\mathrm{d}t,a_{\mathrm{n}}=\frac{1}{L}\int_{-L}^L{f\left( t \right)}\cos \frac{n\pi}{L}t\mathrm{d}t,b_{\mathrm{n}}=\frac{1}{L}\int_{-L}^L{f\left( t \right)}\sin \frac{n\pi}{L}t\mathrm{d}t ⇒f(t)=2a0+n=1∑∞[ancosLnπt+bnsinLnπt],a0=L1∫−LLf(t)dt,an=L1∫−LLf(t)cosLnπtdt,bn=L1∫−LLf(t)sinLnπtdt

4. 傅里叶级数的复数形式
f ( t ) = a 0 2 + ∑ n = 1 ∞ [ a n 1 2 ( e i n w t + e − i n w t ) − b n 1 2 ( e i n w t − e − i n w t ) ] = a 0 2 + ∑ n = 1 ∞ [ a n − i b n 2 e i n w t + a n + i b n 2 e − i n w t ] = ∑ n = 0 0 a 0 2 e i n w t + ∑ n = 1 ∞ a n − i b n 2 e i n w t + ∑ n = − ∞ − 1 a n + i b n 2 e i n w t = ∑ n = − ∞ ∞ C n e i n w t , C n = { a 0 2 n = 0 a n − i b n 2 n = 1 , 2 , 3 , ⋯ a n + i b n 2 n = − 1 , − 2 , − 3 , ⋯ → 1 T ∫ 0 T f ( t ) d t → 1 T ∫ 0 T f ( t ) ( cos n w t − i sin n w t ) d t = 1 T ∫ 0 T f ( t ) ( cos ( − n w t ) + i sin ( − n w t ) ) d t = 1 T ∫ 0 T f ( t ) e − i n w t d t → 1 T ∫ 0 T f ( t ) e − i n w t d t ⇒ f ( t ) = ∑ − ∞ ∞ C n e i n w t , C n = 1 T ∫ 0 T f ( t ) e − i n w t d t f\left( t \right) =\frac{a_0}{2}+\sum_{n=1}^{\infty}{\left[ a_{\mathrm{n}}\frac{1}{2}\left( e^{inwt}+e^{-inwt} \right) -b_{\mathrm{n}}\frac{1}{2}\left( e^{inwt}-e^{-inwt} \right) \right]}=\frac{a_0}{2}+\sum_{n=1}^{\infty}{\left[ \frac{a_{\mathrm{n}}-ib_{\mathrm{n}}}{2}e^{inwt}+\frac{a_{\mathrm{n}}+ib_{\mathrm{n}}}{2}e^{-inwt} \right]} \\ =\sum_{n=0}^0{\frac{a_0}{2}e^{inwt}}+\sum_{n=1}^{\infty}{\frac{a_{\mathrm{n}}-ib_{\mathrm{n}}}{2}e^{inwt}}+\sum_{n=-\infty}^{-1}{\frac{a_{\mathrm{n}}+ib_{\mathrm{n}}}{2}e^{inwt}} \\ =\sum_{n=-\infty}^{\infty}{C_{\mathrm{n}}e^{inwt}},C_{\mathrm{n}}=\begin{cases} \frac{a_0}{2}\,\,n=0\\ \frac{a_{\mathrm{n}}-ib_{\mathrm{n}}}{2}\,\,n=1,2,3,\cdots\\ \frac{a_{\mathrm{n}}+ib_{\mathrm{n}}}{2}\,\,n=-1,-2,-3,\cdots\\ \end{cases}\begin{array}{c} \rightarrow \frac{1}{T}\int_0^T{f\left( t \right)}\mathrm{d}t\\ \rightarrow \frac{1}{T}\int_0^T{f\left( t \right)}\left( \cos nwt-i\sin nwt \right) \mathrm{d}t=\frac{1}{T}\int_0^T{f\left( t \right)}\left( \cos \left( -nwt \right) +i\sin \left( -nwt \right) \right) \mathrm{d}t=\frac{1}{T}\int_0^T{f\left( t \right)}e^{-inwt}\mathrm{d}t\\ \rightarrow \frac{1}{T}\int_0^T{f\left( t \right) e^{-inwt}}\mathrm{d}t\\ \end{array} \\ \Rightarrow f\left( t \right) =\sum_{-\infty}^{\infty}{C_{\mathrm{n}}e^{inwt}},C_{\mathrm{n}}=\frac{1}{T}\int_0^T{f\left( t \right) e^{-inwt}}\mathrm{d}t f(t)=2a0+n=1∑∞[an21(einwt+e−inwt)−bn21(einwt−e−inwt)]=2a0+n=1∑∞[2an−ibneinwt+2an+ibne−inwt]=n=0∑02a0einwt+n=1∑∞2an−ibneinwt+n=−∞∑−12an+ibneinwt=n=−∞∑∞Cneinwt,Cn=⎩ ⎨ ⎧2a0n=02an−ibnn=1,2,3,⋯2an+ibnn=−1,−2,−3,⋯→T1∫0Tf(t)dt→T1∫0Tf(t)(cosnwt−isinnwt)dt=T1∫0Tf(t)(cos(−nwt)+isin(−nwt))dt=T1∫0Tf(t)e−inwtdt→T1∫0Tf(t)e−inwtdt⇒f(t)=−∞∑∞Cneinwt,Cn=T1∫0Tf(t)e−inwtdt
- Euler’s Formula
5. 从傅里叶级数推导傅里叶变换FT
f T ( t ) = f ( t + T ) f_{\mathrm{T}}\left( t \right) =f\left( t+T \right) fT(t)=f(t+T)
f T ( t ) = ∑ − ∞ ∞ C n e i n w 0 t f_{\mathrm{T}}\left( t \right) =\sum_{-\infty}^{\infty}{C_{\mathrm{n}}e^{inw_0t}} fT(t)=∑−∞∞Cneinw0t, 基频率: w 0 = 2 π T w_0=\frac{2\pi}{T} w0=T2π, 定义函数: C n = 1 T ∫ − T 2 T 2 f T ( t ) e − i n w t d t C_{\mathrm{n}}=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{f_{\mathrm{T}}\left( t \right) e^{-inwt}}\mathrm{d}t Cn=T1∫−2T2TfT(t)e−inwtdt
非周期,一般形式: T → ∞ T\rightarrow \infty T→∞
lim T → ∞ f T ( t ) = f ( t ) , Δ w = ( n + 1 ) w 0 − n w 0 = w 0 = 2 π T T ↗ Δ w ↘ \underset{T\rightarrow \infty}{\lim}f_{\mathrm{T}}\left( t \right) =f\left( t \right) ,\varDelta w=\left( n+1 \right) w_0-nw_0=w_0=\frac{2\pi}{T}\,\,T\nearrow \varDelta w\searrow T→∞limfT(t)=f(t),Δw=(n+1)w0−nw0=w0=T2πT↗Δw↘
f T ( t ) = ∑ − ∞ ∞ ( 1 T ∫ − T 2 T 2 f T ( t ) e − i n w 0 t d t ) e i n w 0 t , 1 T = Δ w 2 π ⇒ f T ( t ) = ∑ − ∞ ∞ ( Δ w 2 π ∫ − T 2 T 2 f T ( t ) e − i n w 0 t d t ) e i n w 0 t , T → ∞ : { ∫ − T 2 T 2 d t → ∫ − ∞ ∞ d t n w 0 → w ∑ − ∞ ∞ Δ w → ∫ − ∞ ∞ d w ⇒ f ( t ) = 1 2 π ∫ − ∞ ∞ ( ∫ − ∞ ∞ f ( t ) e − i w t d t ) e i w t d w , ∫ − ∞ ∞ f ( t ) e − i w t d t = F ( w ) ⇒ f ( t ) = 1 2 π ∫ − ∞ ∞ F ( w ) e i w t d w f_{\mathrm{T}}\left( t \right) =\sum_{-\infty}^{\infty}{\left( \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{f_{\mathrm{T}}\left( t \right) e^{-inw_0t}}\mathrm{d}t \right) e^{inw_0t}},\frac{1}{T}=\frac{\varDelta w}{2\pi} \\ \Rightarrow f_{\mathrm{T}}\left( t \right) =\sum_{-\infty}^{\infty}{\left( \frac{\varDelta w}{2\pi}\int_{-\frac{T}{2}}^{\frac{T}{2}}{f_{\mathrm{T}}\left( t \right) e^{-inw_0t}}\mathrm{d}t \right) e^{inw_0t}},T\rightarrow \infty :\begin{cases} \int_{-\frac{T}{2}}^{\frac{T}{2}}{}\mathrm{d}t\rightarrow \int_{-\infty}^{\infty}{}\mathrm{d}t\\ nw_0\rightarrow w\\ \sum_{-\infty}^{\infty}{\varDelta w}\rightarrow \int_{-\infty}^{\infty}{}\mathrm{d}w\\ \end{cases} \\ \Rightarrow f\left( t \right) =\frac{1}{2\pi}\int_{-\infty}^{\infty}{\left( \int_{-\infty}^{\infty}{f\left( t \right) e^{-iwt}}\mathrm{d}t \right)}e^{iwt}\mathrm{d}w,\int_{-\infty}^{\infty}{f\left( t \right) e^{-iwt}}\mathrm{d}t=F\left( w \right) \\ \Rightarrow f\left( t \right) =\frac{1}{2\pi}\int_{-\infty}^{\infty}{F\left( w \right)}e^{iwt}\mathrm{d}w fT(t)=−∞∑∞(T1∫−2T2TfT(t)e−inw0tdt)einw0t,T1=2πΔw⇒fT(t)=−∞∑∞(2πΔw∫−2T2TfT(t)e−inw0tdt)einw0t,T→∞:⎩ ⎨ ⎧∫−2T2Tdt→∫−∞∞dtnw0→w∑−∞∞Δw→∫−∞∞dw⇒f(t)=2π1∫−∞∞(∫−∞∞f(t)e−iwtdt)eiwtdw,∫−∞∞f(t)e−iwtdt=F(w)⇒f(t)=2π1∫−∞∞F(w)eiwtdw
F ( w ) = ∫ − ∞ ∞ f ( t ) e − i w t d t F\left( w \right) =\int_{-\infty}^{\infty}{f\left( t \right) e^{-iwt}}\mathrm{d}t F(w)=∫−∞∞f(t)e−iwtdt : FT 傅里叶变换
f ( t ) = 1 2 π ∫ − ∞ ∞ F ( w ) e i w t d w f\left( t \right) =\frac{1}{2\pi}\int_{-\infty}^{\infty}{F\left( w \right)}e^{iwt}\mathrm{d}w f(t)=2π1∫−∞∞F(w)eiwtdw : 逆变换
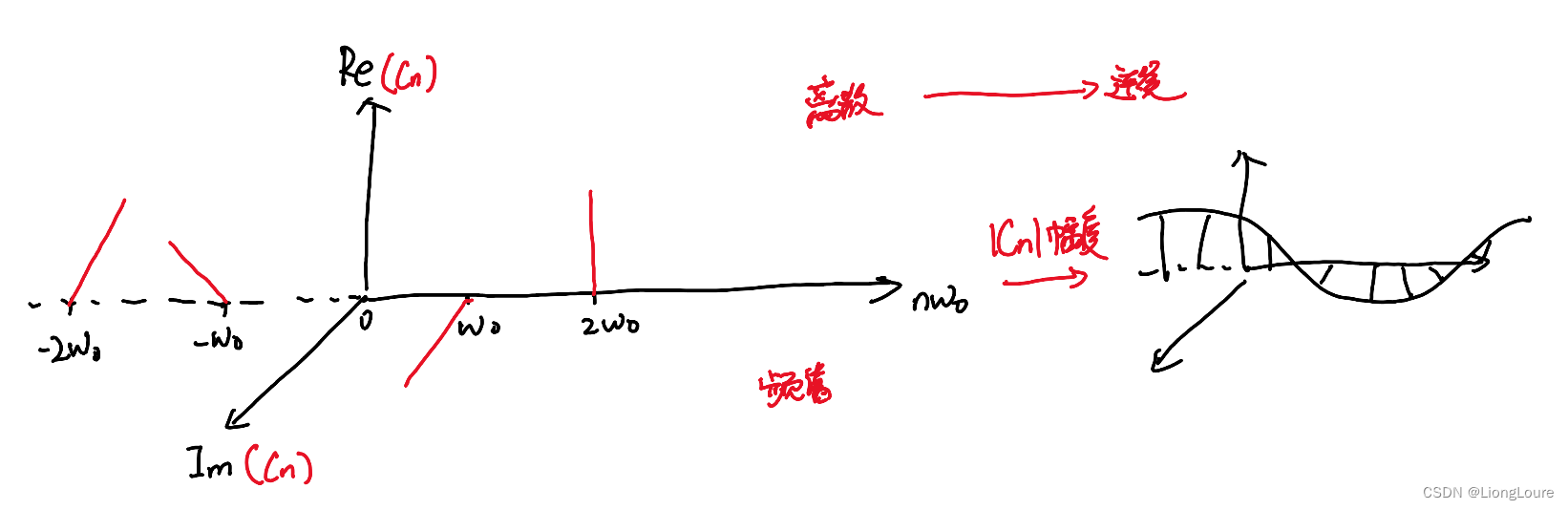
6. 总结
三角函数的正交性:
[ 0 , 1 , sin x , cos x , sin 2 x , cos 2 x , ⋯ , sin n x , cos n x ] , n = 0 , 1 , 2 , ⋯ \left[ 0,1,\sin x,\cos x,\sin 2x,\cos 2x,\cdots ,\sin nx,\cos nx \right] ,n=0,1,2,\cdots [0,1,sinx,cosx,sin2x,cos2x,⋯,sinnx,cosnx],n=0,1,2,⋯
∫ − π π sin n x sin m x d x = 0 , n ≠ m ∫ − π π sin n x sin m x d x = 0 , n ≠ m ∫ − π π sin n x cos m x d x = 0 , n ≠ m \int_{-\pi}^{\pi}{\sin nx\sin mx}\mathrm{d}x=0,n\ne m \\ \int_{-\pi}^{\pi}{\sin nx\sin mx}\mathrm{d}x=0,n\ne m \\ \int_{-\pi}^{\pi}{\sin nx\cos mx}\mathrm{d}x=0,n\ne m ∫−ππsinnxsinmxdx=0,n=m∫−ππsinnxsinmxdx=0,n=m∫−ππsinnxcosmxdx=0,n=m
周期 2 π 2\pi 2π :
f ( x ) = f ( x + 2 π ) f\left( x \right) =f\left( x+2\pi \right) f(x)=f(x+2π)
f ( x ) = ∑ n = 0 ∞ a n cos n x + ∑ n = 0 ∞ b n sin n x ← f ( x ) = a 0 2 + ∑ n = 0 ∞ a n cos n x + ∑ n = 0 ∞ b n sin n x f\left( x \right) =\sum_{n=0}^{\infty}{a_{\mathrm{n}}\cos nx}+\sum_{n=0}^{\infty}{b_{\mathrm{n}}\sin nx}\gets f\left( x \right) =\frac{a_0}{2}+\sum_{n=0}^{\infty}{a_{\mathrm{n}}\cos nx}+\sum_{n=0}^{\infty}{b_{\mathrm{n}}\sin nx} f(x)=n=0∑∞ancosnx+n=0∑∞bnsinnx←f(x)=2a0+n=0∑∞ancosnx+n=0∑∞bnsinnx
a 0 = 1 2 π ∫ − π π f ( x ) d x , a n = 1 π ∫ − π π f ( x ) cos n x d x , b n = 1 π ∫ − π π f ( x ) sin n x d x a_0=\frac{1}{2\pi}\int_{-\pi}^{\pi}{f\left( x \right)}\mathrm{d}x,a_{\mathrm{n}}=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \cos nx}\mathrm{d}x,b_{\mathrm{n}}=\frac{1}{\pi}\int_{-\pi}^{\pi}{f\left( x \right) \sin nx}\mathrm{d}x a0=2π1∫−ππf(x)dx,an=π1∫−ππf(x)cosnxdx,bn=π1∫−ππf(x)sinnxdx
周期 2 L 2L 2L :
T = 2 L , f ( t ) = f ( t + 2 L ) , x = π L t T=2L,f\left( t \right) =f\left( t+2L \right) ,x=\frac{\pi}{L}t T=2L,f(t)=f(t+2L),x=Lπt
f ( t ) = a 0 2 + ∑ n = 1 ∞ [ a n cos n π L t + b n sin n π L t ] f\left( t \right) =\frac{a_0}{2}+\sum_{n=1}^{\infty}{\left[ a_{\mathrm{n}}\cos \frac{n\pi}{L}t+b_{\mathrm{n}}\sin \frac{n\pi}{L}t \right]} f(t)=2a0+n=1∑∞[ancosLnπt+bnsinLnπt]
a 0 = 1 L ∫ − L L f ( t ) d t , a n = 1 L ∫ − L L f ( t ) cos n π L t d t , b n = 1 L ∫ − L L f ( t ) sin n π L t d t a_0=\frac{1}{L}\int_{-L}^L{f\left( t \right)}\mathrm{d}t,a_{\mathrm{n}}=\frac{1}{L}\int_{-L}^L{f\left( t \right)}\cos \frac{n\pi}{L}t\mathrm{d}t,b_{\mathrm{n}}=\frac{1}{L}\int_{-L}^L{f\left( t \right)}\sin \frac{n\pi}{L}t\mathrm{d}t a0=L1∫−LLf(t)dt,an=L1∫−LLf(t)cosLnπtdt,bn=L1∫−LLf(t)sinLnπtdt
复指数:
f ( t ) = ∑ − ∞ ∞ C n e i n w 0 t , w 0 = 2 π T , C n = 1 T ∫ 0 T f ( t ) e − i n w 0 t d t f\left( t \right) =\sum_{-\infty}^{\infty}{C_{\mathrm{n}}e^{inw_0t}},w_0=\frac{2\pi}{T},C_{\mathrm{n}}=\frac{1}{T}\int_0^T{f\left( t \right) e^{-inw_0t}}\mathrm{d}t f(t)=−∞∑∞Cneinw0t,w0=T2π,Cn=T1∫0Tf(t)e−inw0tdt
FT :
f ( t ) = f ( t + T ) , T → ∞ f\left( t \right) =f\left( t+T \right) ,T\rightarrow \infty f(t)=f(t+T),T→∞ , f ( t ) = 1 2 π ∫ − ∞ ∞ ( ∫ − ∞ ∞ f ( t ) e − i w t d t ) e i w t d w f\left( t \right) =\frac{1}{2\pi}\int_{-\infty}^{\infty}{\left( \int_{-\infty}^{\infty}{f\left( t \right) e^{-iwt}}\mathrm{d}t \right)}e^{iwt}\mathrm{d}w f(t)=2π1∫−∞∞(∫−∞∞f(t)e−iwtdt)eiwtdw
F T → F ( w ) = ∫ − ∞ ∞ f ( t ) e − i w t d t I F T → ( t ) = 1 2 π ∫ − ∞ ∞ F ( w ) e i w t d w \begin{array}{c} FT\rightarrow F\left( w \right) =\int_{-\infty}^{\infty}{f\left( t \right) e^{-iwt}}\mathrm{d}t\\ IFT\rightarrow \left( t \right) =\frac{1}{2\pi}\int_{-\infty}^{\infty}{F\left( w \right)}e^{iwt}\mathrm{d}w\\ \end{array} FT→F(w)=∫−∞∞f(t)e−iwtdtIFT→(t)=2π1∫−∞∞F(w)eiwtdw
Laplace : F ( s ) : ∫ − ∞ ∞ f ( t ) e − s t d t F\left( s \right) :\int_{-\infty}^{\infty}{f\left( t \right) e^{-st}}\mathrm{d}t F(s):∫−∞∞f(t)e−stdt
相关文章:

[足式机器人]Part2 Dr. CAN学习笔记 - Ch03 傅里叶级数与变换
本文仅供学习使用 本文参考: B站:DR_CAN Dr. CAN学习笔记-Ch03 傅里叶级数与变换 1. 三角函数的正交性2. 周期为 2 π 2\pi 2π的函数展开为傅里叶级数3. 周期为 2 L 2L 2L的函数展开4. 傅里叶级数的复数形式5. 从傅里叶级数推导傅里叶变换FT6. 总结 1. …...

你想使用域名访问一个ip的网页,你应该怎么办呢?
你想使用域名访问一个ip的网页,你应该怎么办呢? eg:你想用https://test.com/访问http://1.1.1.1/方法: eg:你想用https://test.com/访问http://1.1.1.1/ 方法: 1.首先,如果你是服务器的管理者,你需要在服务器的官网申请一个test.com的域名,然后在官网将域名映射到1.1.1.1上. …...
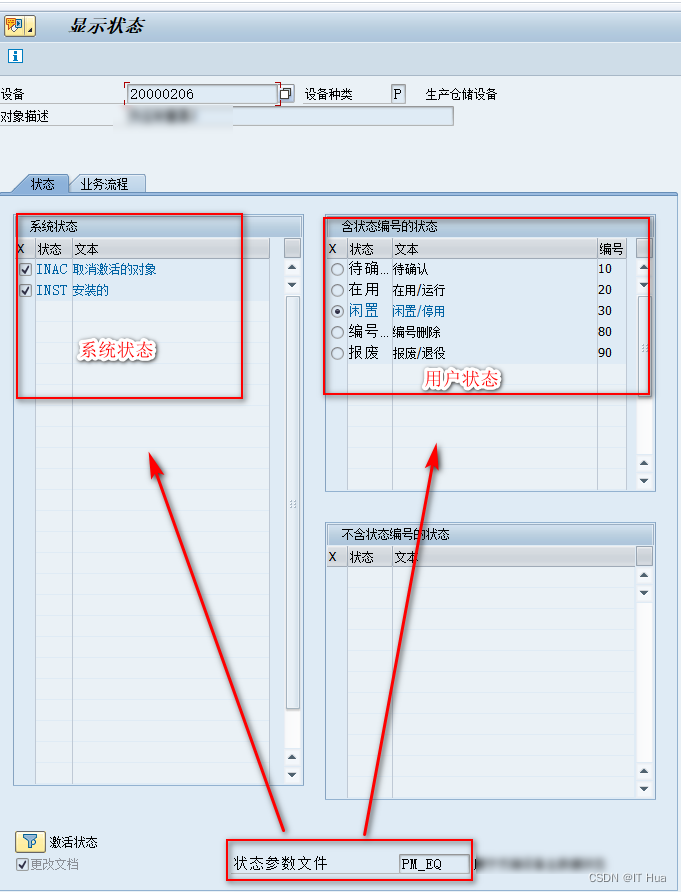
SAP存放状态的几个常用表
SAP存放状态的几个常用表 在sap中,包括订单、项目、计划、设备主数据等,存在审批流程的业务单据,这些业务对象都会有状态的属性,用来控制和约束该业务当前的操作。 主要的表 JEST:存放了该对象编号的当前状态 JCDS…...

AUTO SEG-LOSS SEARCHING METRIC SURROGATES FOR SEMANTIC SEGMENTATION
AUTO SEG-LOSS: 搜索度量替代语义分割 论文链接:https://arxiv.org/abs/2010.07930 项目链接:https://github.com/fundamentalvision/Auto-Seg-Loss ABSTRACT 设计合适的损失函数是训练深度网络的关键。特别是在语义分割领域,针对不同的场…...

openssl3.2 - 官方demo学习 - 索引贴
文章目录 openssl3.2 - 官方demo学习 - 索引贴概述笔记工程的搭建和调试环境BIOBIO - client-arg.cBIO - client-conf.cBIO - saccept.cBIO - sconnect.cBIO - server-arg.cBIO - server-cmod.cBIO - server-conf.cBIO - 总结certsciphercipher - aesccm.ccipher - aesgcm.ccip…...

textarea文本框根据输入内容自动适应高度
第一种: <el-input auto-completeoff typetextarea :autosize"{minRows:3,maxRows:10}" class"no-scroll"> </el-input> /* 页面的样式表 */ .no-scroll textarea {overflow: hidden; /* 禁用滚动条 */resize: none; /* 禁止用户…...
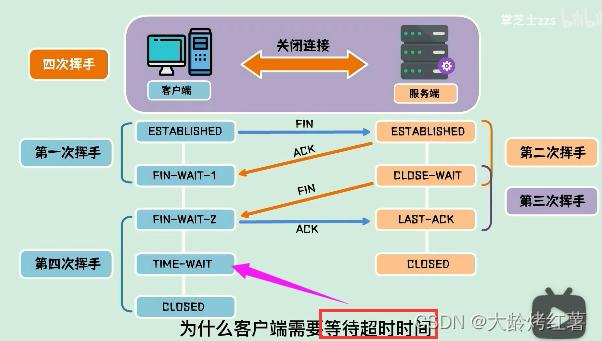
【JAVA基础--计算机网络】--TCP三次握手+四次挥手
三次握手四次挥手 写在前面1. 三次握手1.1 作用: 为了在不可靠的信道上建立起可靠的连接;1.2 建立过程1.3 面试提问 2. 四次挥手2.1 作用:为了在不可靠的网络信道中进行可靠的连接断开确认2.2 断开过程2.3 面试提问 写在前面 三次握手建立连…...
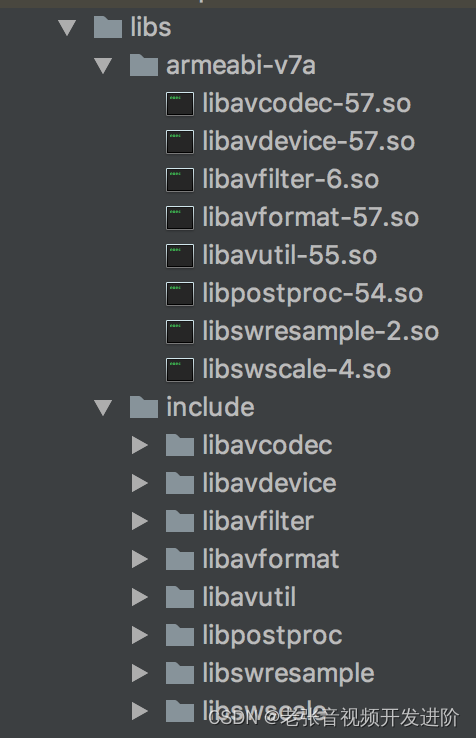
最新靠谱可用的-Mac-环境下-FFmpeg-环境搭建
最近在尝试搭建 FFmpeg 开发环境时遇到一个蛋疼的事,Google 了 N 篇文章竟然没有一篇是可以跑起来的! 少部分教程是给出了自我矛盾的配置(是的,按照贴出来的代码和配置,他自己都跑不起来),大部…...

【漏洞复现】Hikvision SPON IP网络对讲广播系统存在命令执行漏洞CVE-2023-6895
漏洞描述 Hikvision Intercom Broadcasting System是中国海康威视(Hikvision)公司的一个对讲广播系统。 Hikvision Intercom Broadcasting System是中国海康威视(Hikvision)公司的一个对讲广播系统。Hikvision Intercom Broadcasting System 3.0.3_20201113_RELEASE(HIK)版…...

微软为Windows内置记事本应用开发AI功能;2024年15个 AI 语音生成器
🦉 AI新闻 🚀 微软为Windows内置记事本应用开发AI功能 摘要:微软正在开发一个新的生成式AI功能,名为"Cowriter",用于Windows内置的记事本应用。该功能类似于画图应用中的"Cocreator"功能&#x…...
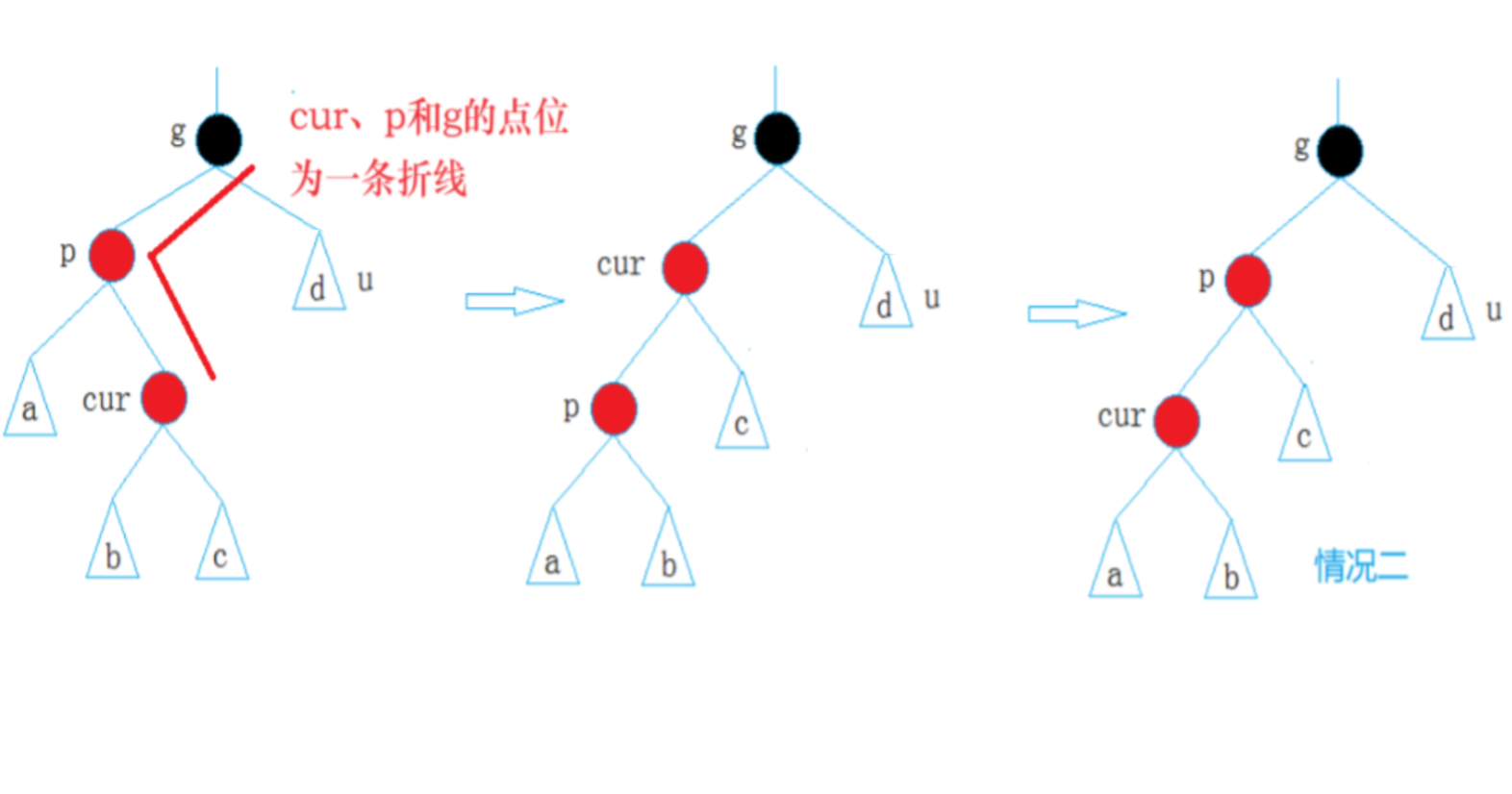
【C++进阶06】红黑树图文详解及C++模拟实现红黑树
一、红黑树的概念及性质 1.1 红黑树的概念 AVL树用平衡因子让树达到高度平衡 红黑树可以认为是AVL树的改良 通过给每个节点标记颜色让树接近平衡 以减少树在插入节点的旋转 在每个结点新增一个存储位表示结点颜色 可以是Red或Black 通过对任何一条从根到叶子的路径上 各个结点…...

2023年最严重的10起0Day漏洞攻击事件
根据谷歌公司威胁分析小组去年 7 月发布的报告显示,2022 年全球共有 41 个 0day 漏洞被利用和披露。而研究人员普遍认为,2023 年被利用的 0Day 漏洞数量会比 2022 年更高,这些危险的漏洞被广泛用于商业间谍活动、网络攻击活动以及数据勒索攻击…...

Linux之Iptables简易应用
文档形成时期:2009-2024年 和iptables打交道有15年了,经过无数实践后,形成一个简易应用文档。 文档主题是简易应用,所以其原理不详述了。 因软件世界之复杂和个人能力之限,难免疏漏和错误,欢迎指正。 文章目…...

树状结构查询 - 华为OD统一考试
OD统一考试 分值: 200分 题解: Java / Python / C++ 题目描述 通常使用多行的节点、父节点表示一棵树,比如: 西安 陕西 陕西 中国 江西 中国 中国 亚洲 泰国 亚洲 输入一个节点之后,请打印出来树中他的所有下层节点。 输入描述 第一行输入行数,下面是多行数据,每行以…...
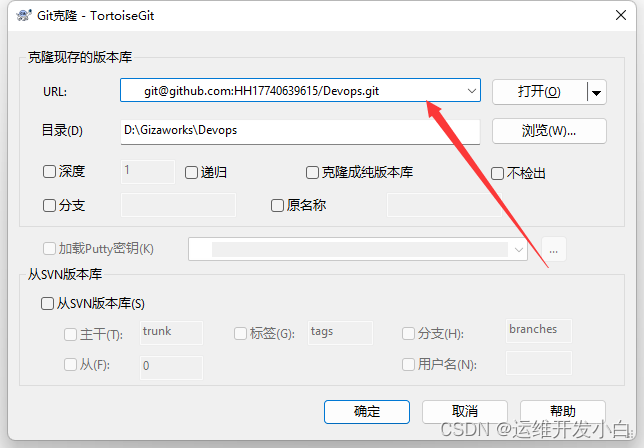
版本控制系统教程
1.Git的基本介绍 1.1 Git的概念 Git是一个开源的分布式版本控制系统,用于敏捷高效地处理任何或小或大的项目.Git是Linus Torvalds为了帮助管理Linux内核开发而开发的一个开放源码的版本控制软件.Git与常用的版本控制工具CVS,Subversion等不同ÿ…...

Java多线程并发篇----第十篇
系列文章目录 文章目录 系列文章目录前言一、start 与 run 区别二、JAVA 后台线程三、什么是乐观锁前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站,这篇文章男女通用,看懂了就去分享给你的码吧。 一、start 与 r…...

模型\视图一般步骤:为什么经常要用“选择模型”QItemSelectionModel?
一、“使用视图”一般的步骤: //1.创建 模型(这里是数据模型!) tabModelnew QSqlTableModel(this,DB);//数据表 //2.设置 视图的模型(这里是数据模型!) ui->tableView->setModel(tabModel); 模型种类: QStringListModel…...
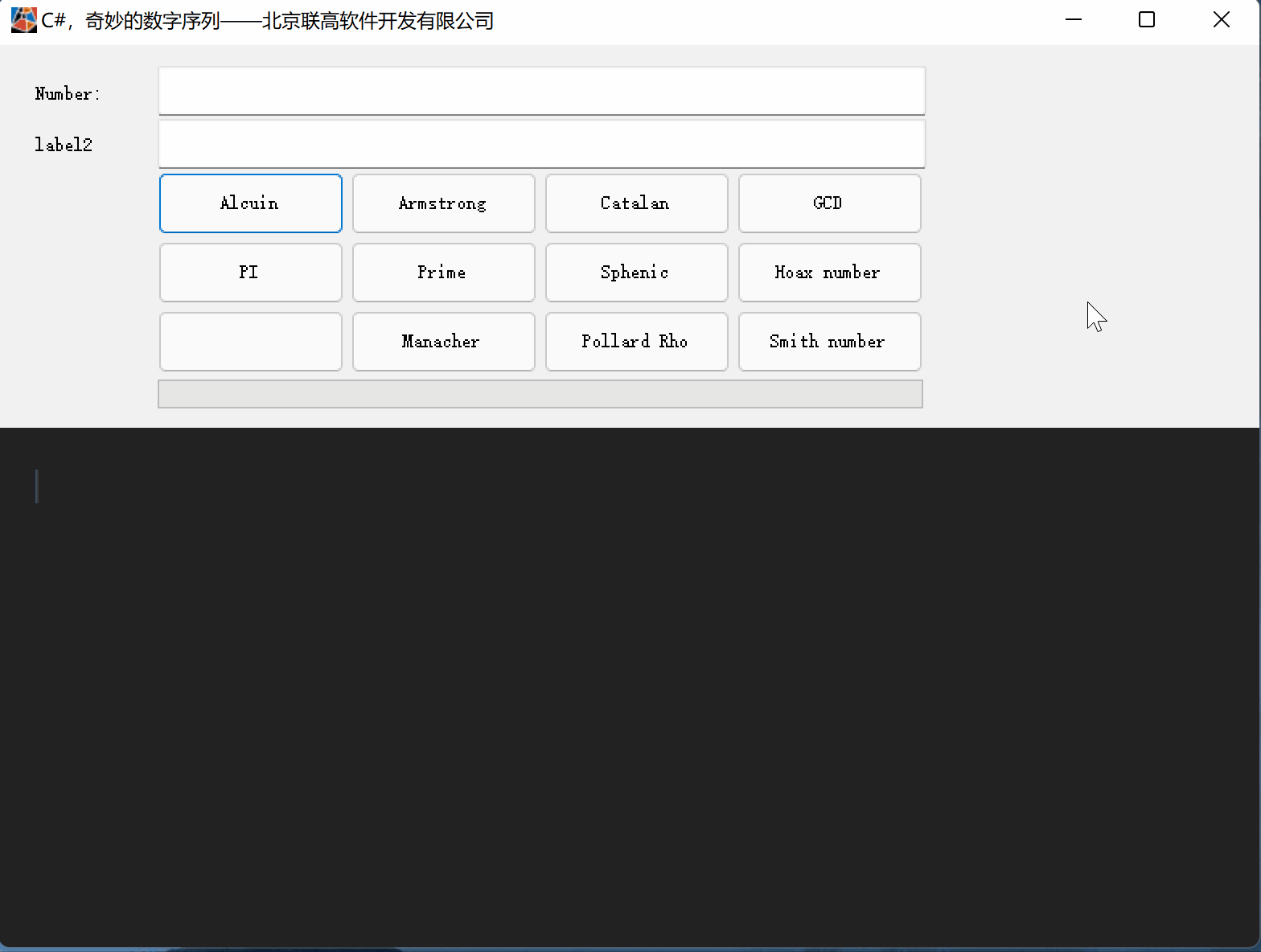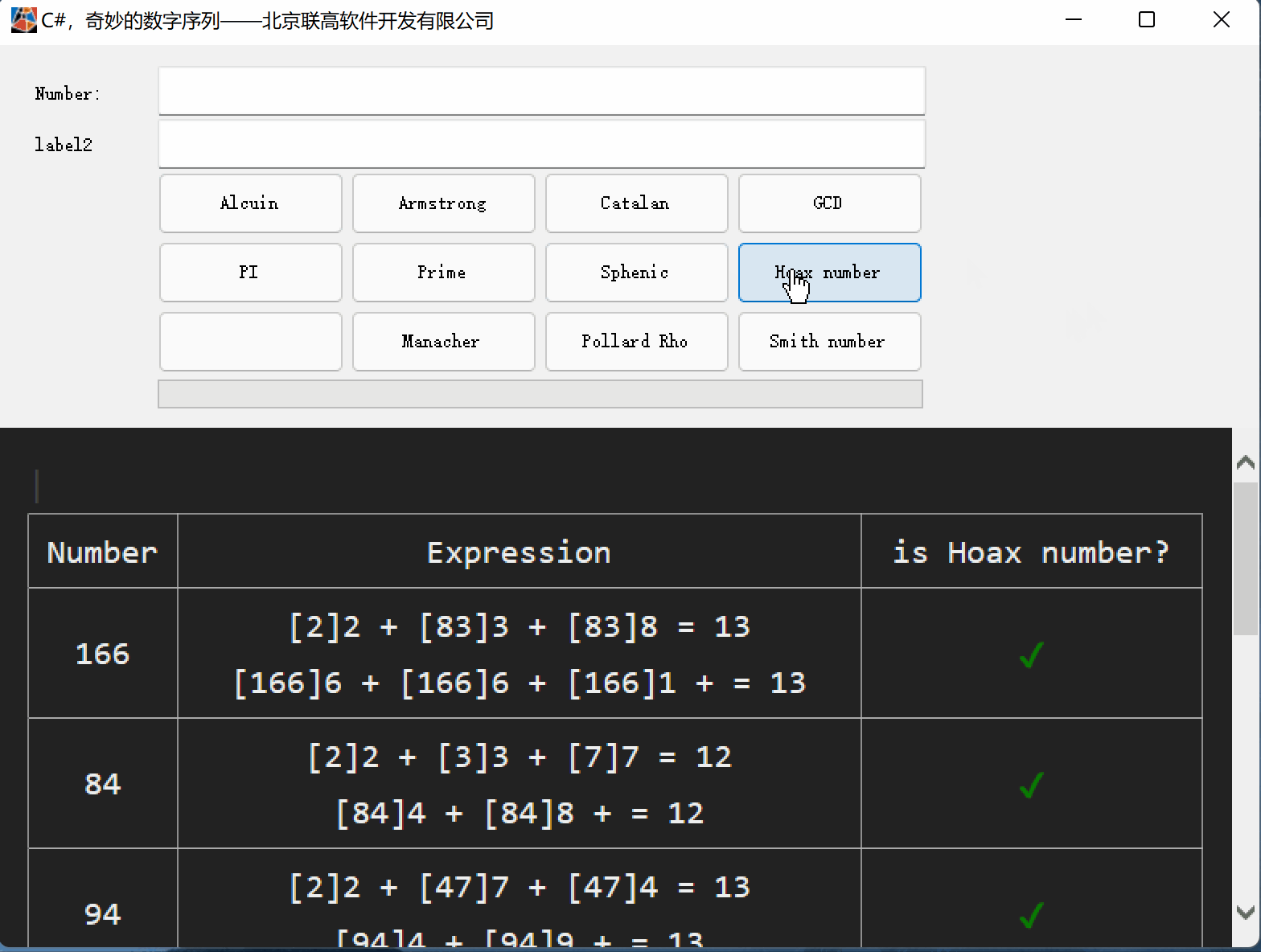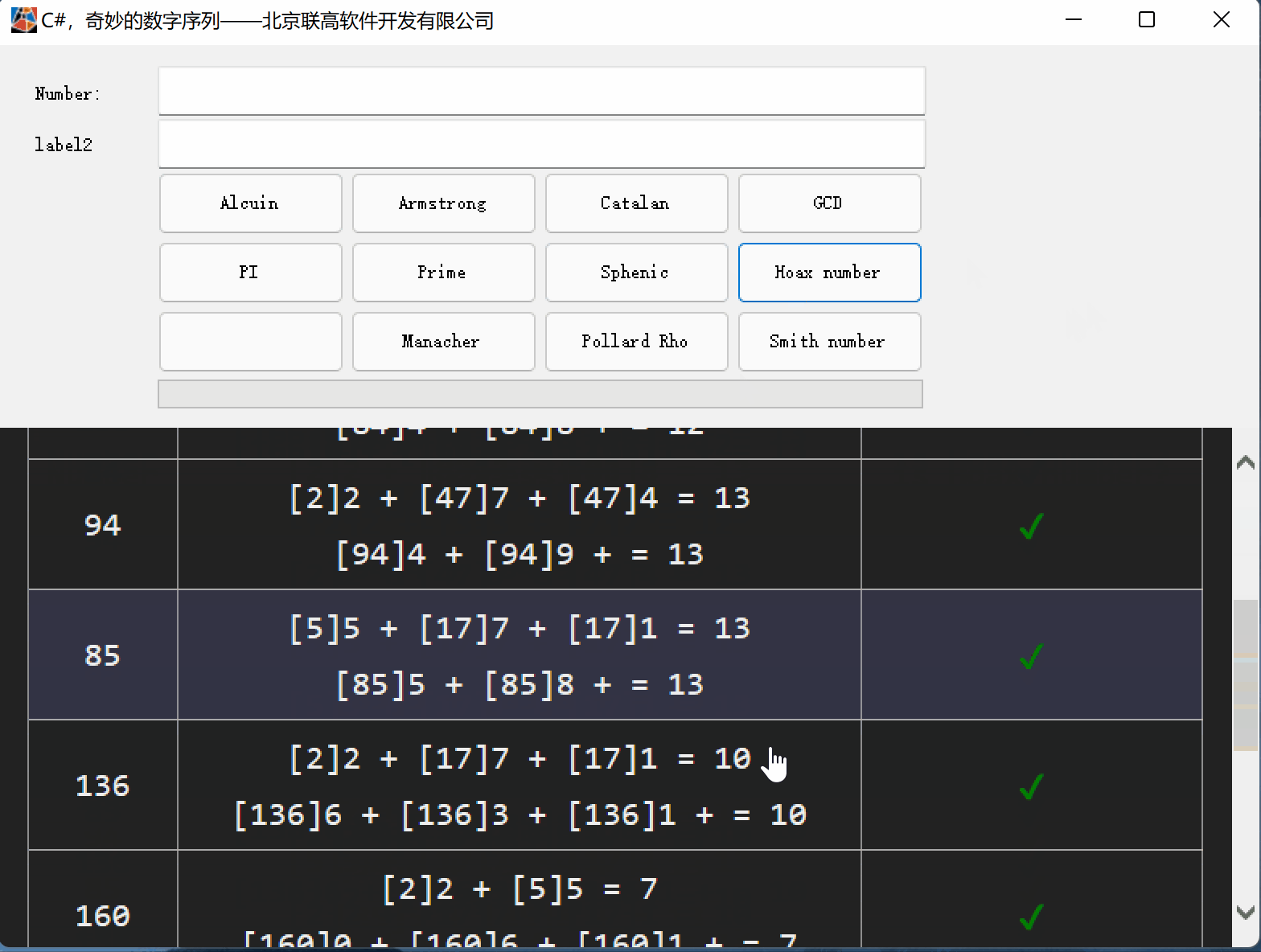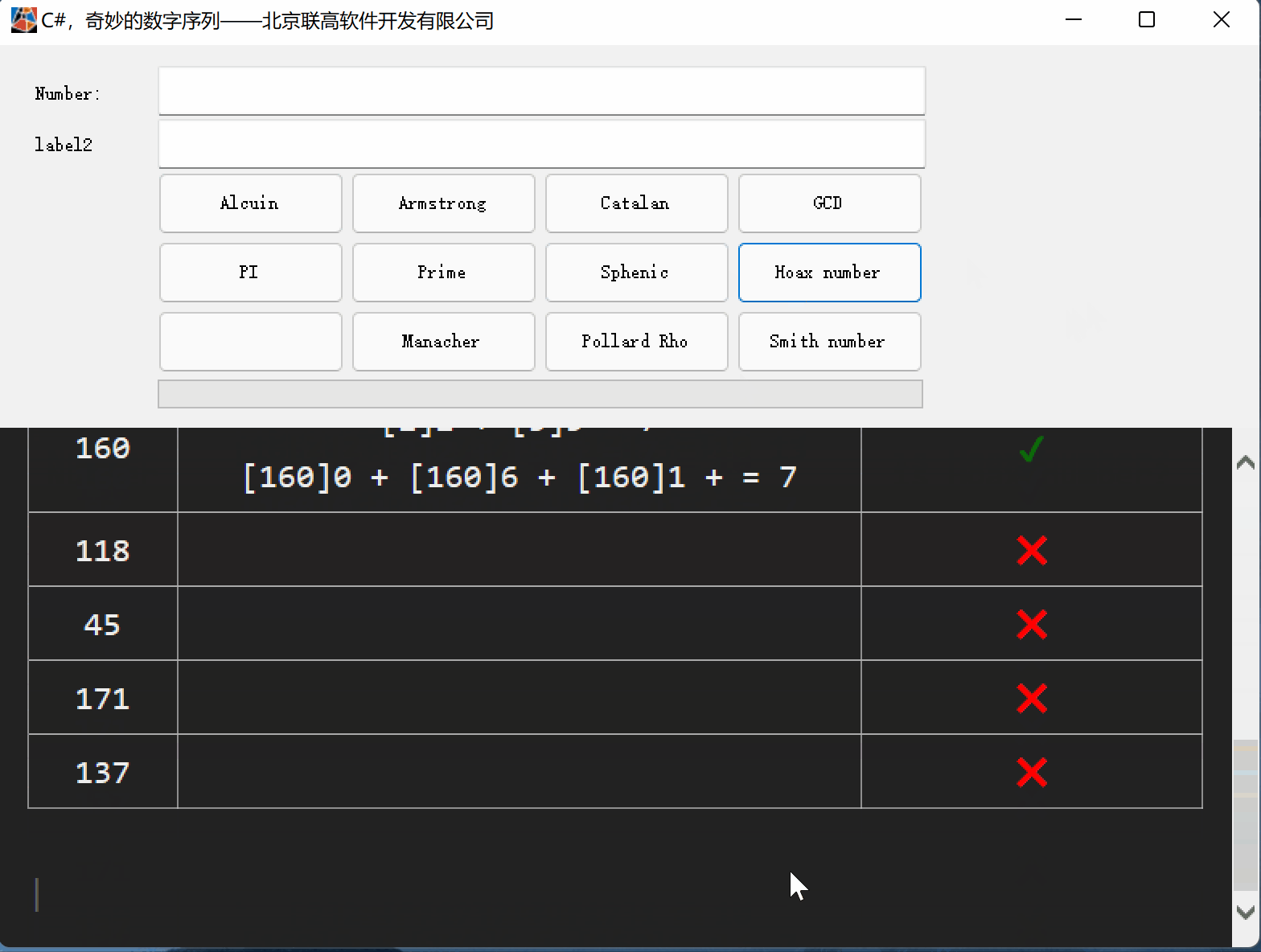
C#,愚弄数(Hoax Number)的计算方法与源代码
一、愚弄数(Hoax Number) 愚弄数(Hoax Number)是一种组合数字, 其数字总和等于其不同质因数的数字总和。 注:1不被视为质数, 因此它不包含在不同质因数的总和中。 有些愚弄数(Hoax Number)数字也…...

c JPEG编码,此程序没有处现MCU中亮度分量的排序
#include <stdio.h> #include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> #include <stdlib.h> #include <unistd.h> #include <sys/ioctl.h> #include <linux/videodev2.h> //v4l2 头文件 #include <strin…...
前端规范扩展
前端编程规范是基于原有vue2基础上那套《编码风格及标准》上,应用于vue3、typescript、vite2基础上延伸出来的扩展补充,持续完善 一、编码规范 ESLint 代码检测工具 Pretter 代码格式化工具配合双校验代码 Git 规范 - 编码工具 vscode 同步参考文档中…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...
