计算机图形学:改进的中点BH算法

作者:非妃是公主
专栏:《计算机图形学》
博客地址:https://blog.csdn.net/myf_666
个性签:顺境不惰,逆境不馁,以心制境,万事可成。——曾国藩
文章目录
- 专栏推荐
- 专栏系列文章
- 序
- 一、改进缘由
- 二、算法原理
- 三、OpenGL代码实现
- 四、实现效果图
- the end……
专栏推荐
| 专栏名称 | 专栏地址 |
|---|---|
| 软件工程 | 专栏——软件工程 |
| 计算机图形学 | 专栏——计算机图形学 |
| 操作系统 | 专栏——操作系统 |
| 软件测试 | 专栏——软件测试 |
| 机器学习 | 专栏——机器学习 |
| 数据库 | 专栏——数据库 |
| 算法 | 专栏——算法 |
专栏系列文章
| 文章名称 | 文章地址 |
|---|---|
| 直线生成算法(DDA算法) | 计算机图形学01——DDA算法 |
| 中点BH算法绘制直线 | 计算机图形学02——中点BH算法 |
| 改进的中点BH算法 | 计算机图形学03——改进的中点BH算法 |
| 中点Bresenham画椭圆 | 计算机图形学04——中点BH绘制椭圆 |
| 中点BH算法绘制任意斜率直线 | 计算机图形学05——中点BH算法绘制任意斜率的直线 |
| 中点Bresenham画圆 | 计算机图形学06——中点BH算法画圆 |
| 有效边表法的多边形扫描转换 | 计算机图形学07——有效边表法绘制填充多边形 |
| 中点BH算法绘制抛物线 100x=y2100x = y^2100x=y2 | 计算机图形学08——中点BH绘制抛物线 |
| 二维观察之点的裁剪 | 计算机图形学09——二维观察之点裁剪 |
| 二维观察之线的裁剪 | 计算机图形学10——二维观察之线裁剪 |
| 二维观察之多边形的裁剪 | 计算机图形学11——二维观察之多边形裁剪 |
| 二维图形的几何变换 | 计算机图形学12——二维图形几何变换 |
| 三维图形的几何变换 | 计算机图形学13——三维图形几何变换 |
| 三维图形的投影变换 | 计算机图形学14——三维图形投影变换 |
序
计算机图形学(英语:computer graphics,缩写为CG)是研究计算机在硬件和软件的帮助下创建计算机图形的科学学科,是计算机科学的一个分支领域,主要关注数字合成与操作视觉的图形内容。虽然这个词通常被认为是指三维图形,事实上同时包括了二维图形以及影像处理。
一、改进缘由
为什么需要改进中点BH算法呢?因为上一篇(计算机图形学02:中点BH算法绘制直线)已经提到,中点BH算法会带来浮点数的问题,而浮点数对于硬件的运算不仅实现复杂,而且运行起来效率低下。因此,我们需要对其进行改进,也就诞生了改进的中点BH算法。
二、算法原理
d的含义发生了改变,不再是中点了




改进点1将右半部分的0.5去掉了

这样通过改进的BH算法,去掉了小数,这是一种改进方法。上一篇中也存在着去整改进,为什么有两种改进方法呢?(上一篇文章地址:计算机图形学02:中点BH算法绘制直线)
我并不清楚,也没有进一步检索,知道的小伙伴可以把答案放在评论区!我会补上。
但我猜测,最初的BH算法应该是没有进行化整的,后面在实际硬件运算中发现了问题,因而出现了2种改进方法,一种是上文提到的(叫做中点BH算法的化整改进),另一种就是本文提到的,叫做改进的中点BH算法= =。(不过这只是一种猜测……)
三、OpenGL代码实现
// 改进的Bresenham算法绘制直线段(0≤k≤1)
void Bhline(int x0, int y0, int x1, int y1) {int x, y, dx, dy, e;if (x0 > x1) { // x0为起始点,x1为终止点x = x1; x1 = x0; x0 = x; y = y1; y1 = y0; y0 = y;}dx = x1 - x0; dy = y1 - y0; x = x0; y = y0;e = -dx;glBegin(GL_POINTS);while (x <= x1) {glVertex2i(x, y);x++;e = e + 2 * dy; // e = e + 2dx * kif (e > 0) {y++;e = e - 2 * dx; // e = e - 1}}glEnd();
}
四、实现效果图
运行代码后,调用函数,效果如下:

the end……
改进的中点BH算法到这里就要结束啦~~到此既是缘分,欢迎您的点赞、评论、收藏!关注我,不迷路,我们下期再见!!
😘😘😘 我是Cherries,一位计算机科班在校大学生,写博客用来记录自己平时的所思所想!
💞💞💞 内容繁杂,又才疏学浅,难免存在错误,欢迎各位大佬的批评指正!
👋👋👋 我们相互交流,共同进步!
注:本文由
非妃是公主发布于https://blog.csdn.net/myf_666,转载请务必标明原文链接:https://blog.csdn.net/myf_666/article/details/128164331
相关文章:

计算机图形学:改进的中点BH算法
作者:非妃是公主 专栏:《计算机图形学》 博客地址:https://blog.csdn.net/myf_666 个性签:顺境不惰,逆境不馁,以心制境,万事可成。——曾国藩 文章目录专栏推荐专栏系列文章序一、改进缘由二、…...
:从执行计划看NOT IN、NOT EXISTS 和 LEFT JOIN效率,记住内外关联条件不要乱放)
【SQL开发实战技巧】系列(六):从执行计划看NOT IN、NOT EXISTS 和 LEFT JOIN效率,记住内外关联条件不要乱放
系列文章目录 【SQL开发实战技巧】系列(一):关于SQL不得不说的那些事 【SQL开发实战技巧】系列(二):简单单表查询 【SQL开发实战技巧】系列(三):SQL排序的那些事 【SQL开发实战技巧…...

十分钟利用环信WebIM-vue3-Demo,打包上线一个即时通讯项目【含音视频通话】
这篇文章无废话,只教你如果接到即时通讯功能需求,十分钟利用环信WebIM-vue3-Demo,打包上线一个即时通讯项目【包含音视频通话功能】。 写这篇文章是因为,结合自身情况,以及所遇到的有同样情况的开发者在接到即时通讯&a…...
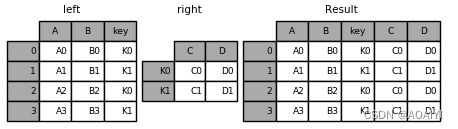
pandas——DataFrame基本操作(二)【建议收藏】
pandas——DataFrame基本操作(二) 文章目录pandas——DataFrame基本操作(二)一、实验目的二、实验原理三、实验环境四、实验内容五、实验步骤1.修改数据2.缺失值3.合并1.concat合并2.使用append方法合并3.使用merge进行合并4.使用…...

PostgreSQL查询引擎——General Expressions Grammar之restricted expression
General expressions语法规则定义在src/backend/parser/gram.y文件中,其是表达式语法的核心。有两种表达式类型:a_expr是不受限制的类型,b_expr是必须在某些地方使用的子集,以避免移位/减少冲突。例如,我们不能将BETWE…...

从某种程度上来看,产业互联网是一次对于互联网的弥补和修正
如果对当下我们正在经历的这样一个时代进行一次定义的话,我更加愿意将其划归到产业互联网的范畴里。可能有人会说,这与产业互联网并无联系,因为从本质上来看,当下我们所经历的这样一个时代,其实是与互联网并没有太多联…...

【C#Unity题】1.委托和事件在使用上的区别是什么?2.C#中 == 和 Equals 的区别是什么?
1.委托和事件在使用上的区别是什么? 委托和事件是C#中的重要概念,通俗来讲,委托是一个可以指向特定方法的指针,可以将委托分配给不同的脚本,使它们能够完成不同的任务。而事件则是一种使用委托实现的通知机制ÿ…...

FFmpeg5.0源码阅读——内存池AVBufferPool
摘要:FFmpeg中大多数数据存储比如AVFrame,AVPacket都是通过AVBufferRef管理的,而承载数据的结构为AVBuffer。本文主要通过FFmpeg源码来分析下FFmpeg中AVBuffer相关的实现。 关键字:AVBuffer、AVBufferPool、AVBufferPool 1. AVBufferRef 1.…...

Python学习------起步7(字符串的连接、删除、修改、查询与统计、类型判断及字符串字母大小写转换)
目录 前言: 1.字符串的连接 join() 函数 2.字符串的删除&取代 replace()函数 3.字符串的修改&切割 (1)strip() 函数 (2)lstrip()函数 和 rstrip()函数 (3)split()函数-->…...
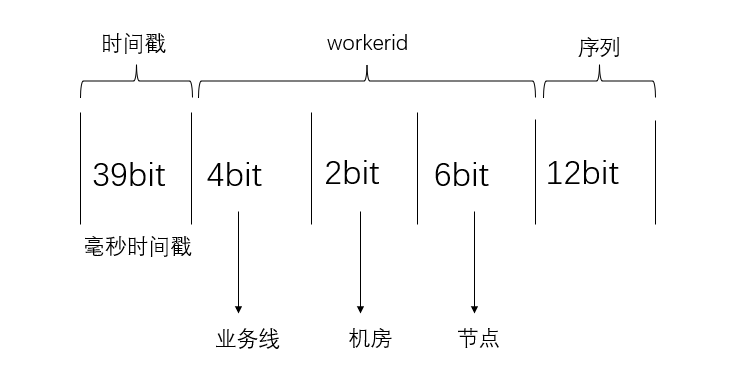
雪花算法snowflake
snowflake中文的意思是 雪花,雪片,所以翻译成雪花算法。它最早是twitter内部使用的分布式环境下的唯一ID生成算法。在2014年开源。雪花算法产生的背景当然是twitter高并发环境下对唯一ID生成的需求,得益于twitter内部高超的技术,雪…...

Part 4 描述性统计分析(占比 10%)——上
文章目录【后续会持续更新CDA Level I&II备考相关内容,敬请期待】【考试大纲】【考试内容】【备考资料】1、统计基本概念1.1、统计学的含义及应用1.1.1、统计学的含义1.2.1、统计学的应用1.2、统计学的基本概念1.2.1、数据及数据的分类1.2.2、总体和样本1.2.3、…...
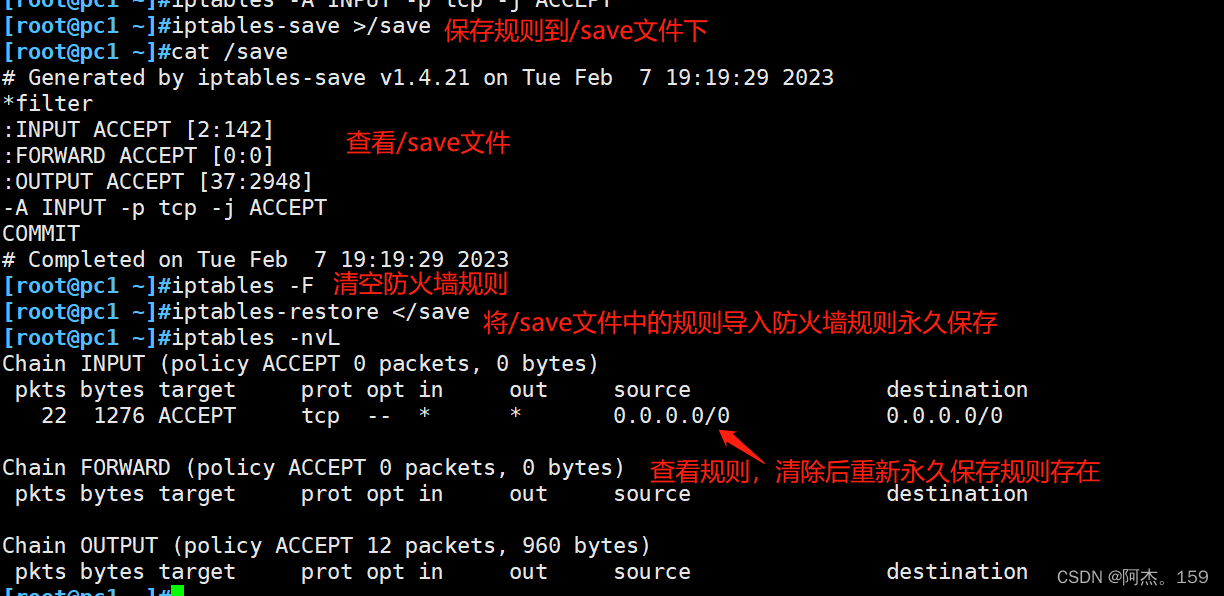
Linux系统安全:安全技术和防火墙
目录 一、安全技术 1、安全技术 2、防火墙分类 二、防火墙 1、iptables五表五链 2、黑白名单 3、iptables基本语法 4、iptables选项 5、控制类型 6、隐藏扩展模块 7、显示扩展模块 8、iptables规则保存 9、自定义链使用 一、安全技术 1、安全技术 ①入侵检测系统…...

【干货】Python:turtle库的用法
【干货】Python:turtle库的用法1. turtle库概述2. turtle库与基本绘图2.1 导入库的三种方式2.1.12.1.22.1.32.2 窗体函数2.2 画笔状态函数2.2.1 seed(s)2.2.2 random()2.2.3 randint(a, b)2.2.4 getrandbits(k)2.2.5 randrange(start, stop[ , step])2.2.6 uniform(…...

信息安全与网络安全有什么区别?
生活中我们经常会听到要保障自己的或者企业的信息安全。那到底什么是信息安全呢?信息安全包含哪些内容?与网络安全又有什么区别呢?今天我们就一起来详细了解一下。什么叫做信息安全?信息安全定义如下:为数据处理系统建…...

花了5年时间,用过市面上95%的工具,终于找到这款万能报表工具
经常有粉丝问我有“哪个报表工具好用易上手?”或者是“有哪些适合绝大多数普通职场人的万能报表工具?” 从这里我大概总结出了大家选择报表工具最期望满足的3点: (1)简单易上手:也就是所谓的学习门槛要低…...

ESP32S3系列--SPI主机驱动详解(一)
一、目的SPI是一种串行同步接口,可用于与外围设备进行通信。ESP32S3自带4个SPI控制器外设,其中SPI0/SPI1内部专用,共用一组信号线,通过一个仲裁器访问外部Flash和PSRAM;SPI2/3各自使用一组信号线;开发者可以使用SPI2/3控制外部SPI…...

2023开工开学火热!远行的人们,把淘特箱包送上顶流
春暖花开,被疫情偷走的三年在今年开学季找补回来了。多个数据反馈,居民消费意愿大幅提升。在淘特上,开工开学节点就很是明显:1月30日以来,淘特箱包品类甚至远超2022年双11,成为开年“第一爆品”。与此同时&…...
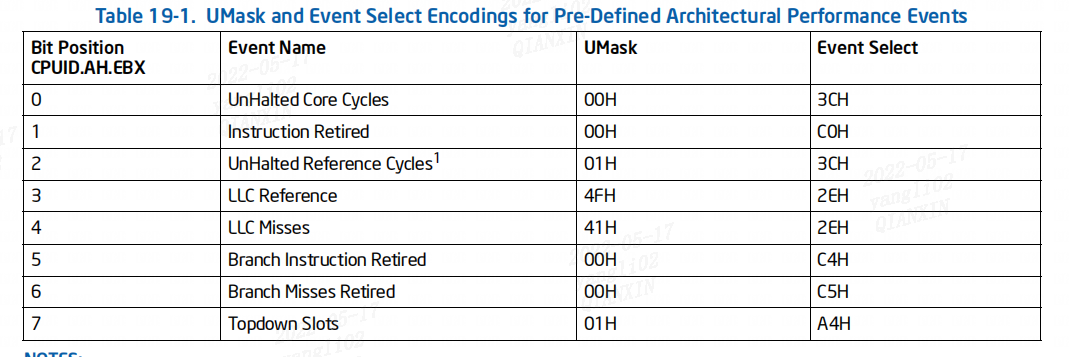
Intel x86_64 PMU简介
文章目录前言一、性能监控概述二、CPUID information三、架构性能监控3.1 架构性能监控 Version 13.1.1 架构性能监控 Version 1 Facilities3.1.2 预定义的体系结构性能事件3.1.3 cmask demo测试参考资料前言 Intel 64 和 IA-32 架构提供了 PMU(Performance Monito…...
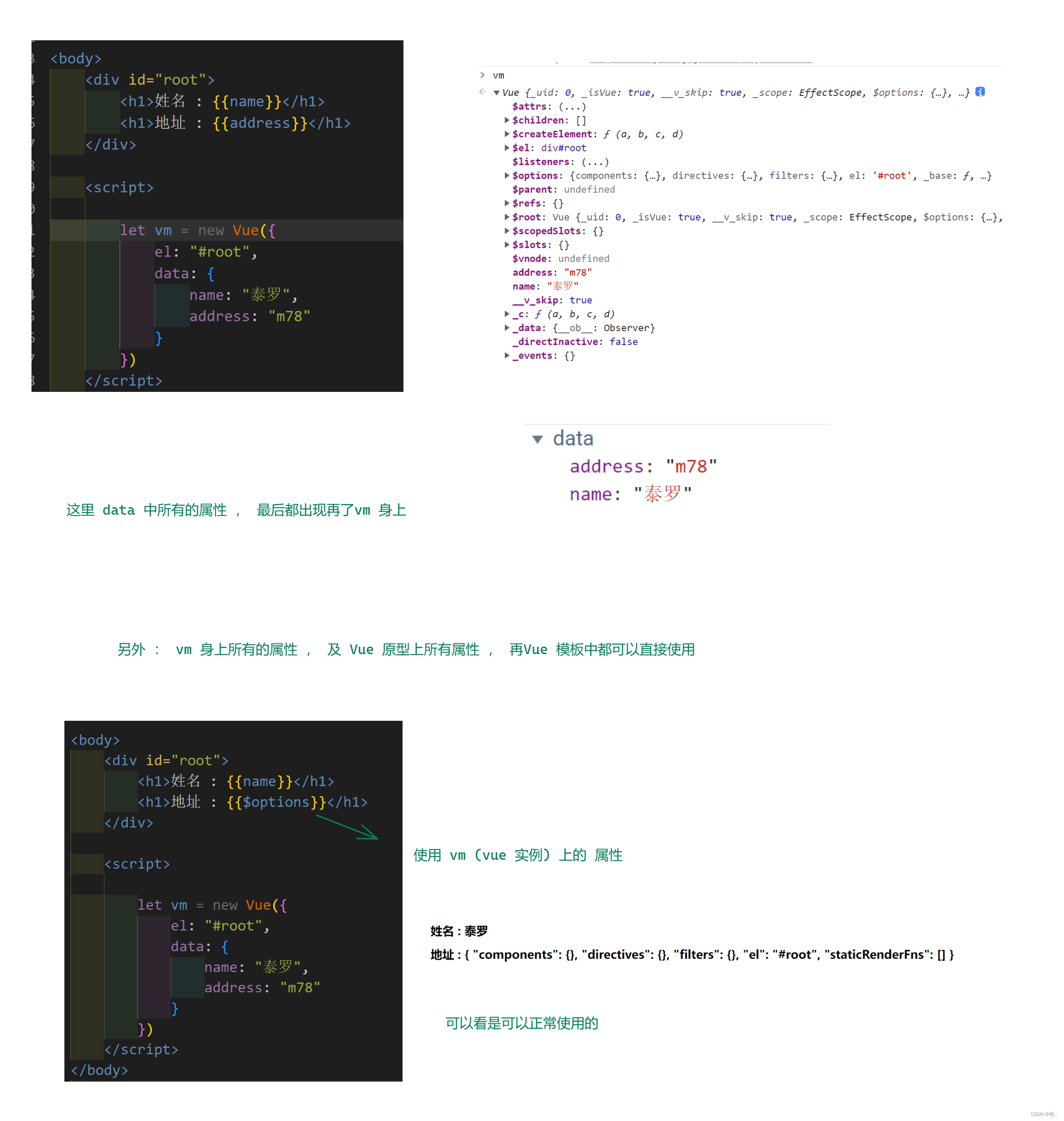
Vue (2)
文章目录1. 模板语法1.1 插值语法1.2 指令语法2. 数据绑定3. 穿插 el 和 data 的两种写法4. MVVM 模型1. 模板语法 root 容器中的代码称为 vue 模板 1.1 插值语法 1.2 指令语法 图一 : 简写 : v-bind: 是可以简写成 : 的 总结 : …...

ESP8266 + STC15基于AT指令通过TCP通讯协议获取时间
ESP8266 + STC15基于AT指令通过TCP通讯协议获取时间 如果纯粹拿32位的ESP8266模块给8位的单片机仅供授时工具使用,有点大材小用了。这里不讨论这个拿esp8266来单独开发使用。本案例只是通过学习esp8266 AT指令功能来验证方案的可行性。 🔖STC15 单片机采用的是:STC15F2K60S…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

Linux基础开发工具——vim工具
文章目录 vim工具什么是vimvim的多模式和使用vim的基础模式vim的三种基础模式三种模式的初步了解 常用模式的详细讲解插入模式命令模式模式转化光标的移动文本的编辑 底行模式替换模式视图模式总结 使用vim的小技巧vim的配置(了解) vim工具 本文章仍然是继续讲解Linux系统下的…...

