《程序员面试金典(第6版)》面试题 02.01. 移除重复节点
题目描述
编写代码,移除未排序链表中的重复节点。保留最开始出现的节点。
示例1:
- 输入:[1, 2, 3, 3, 2, 1]
输出:[1, 2, 3]
-示例2:
输入:[1, 1, 1, 1, 2]
输出:[1, 2]
提示:
- 链表长度在[0, 20000]范围内。
链表元素在[0, 20000]范围内。
进阶:
- 如果不得使用临时缓冲区,该怎么解决?
解题思路与代码
首先,这道题于本质上是要让你删除一些重复的节点。那么删除一个节点需要做哪些操作呢?
首先本题给的是单链表。如果要删除某个节点,则要找到当前节点的前驱节点,使前驱节点的next指针指向当前节点的下一个节点,最后将当前节点的内存释放掉,至此,删除某个节点的操作才算正式完成。
哈希法
因为要删除一个节点,我们就要用该节点的前驱节点去指向该节点的下一个节点。所以,我们就先设立一个要被处理元素的前驱节点,然后依次遍历被处理元素这个节点。如果被处理元素需要被删除,那我们直接用前驱节点删除好了。
为什么要叫哈希法呢?这是因为用到了unordered_set这种无序的关联容器。当我们为在这个集合中找到这个未处理元素时,我们就将这个元素添加到这个集合中去。如果找到了呢?就直接那被处理元素的前驱节点去删除这个节点就好了。这就是这道题的完整思想,剩下的请看代码:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode* removeDuplicateNodes(ListNode* head) {if(head == nullptr) return head;unordered_set<int> set = {head->val};ListNode* pos = head;while(pos->next != nullptr){ListNode* cur = pos->next; //即将要删除的节点if(set.find(cur->val) == set.end()){set.insert(cur->val);pos = cur;}else{pos->next = cur->next;delete cur;}}return head;}
};
复杂度分析:
-
时间复杂度O(N),因为只用了一个while循环,其中N是给定链表的节点数目。
-
空间复杂度O(N),因为最坏情况下,集合中的元素都不相同,我们要存储所有的元素到集合中。
进阶:不使用临时缓冲区
说到不使用临时缓冲区,其实它的意思就是让我直接对链表进行操作。那么如果想象成删除一个string中重复出现的字符了话,这道题其实用两个for循环暴力破解了就行。但这道题是在链表上进行操作,我们就要将双层for循环,去改成双层while循环。
这解题思路还是与哈希法类似,一共需要设立3个节点。
第一个节点作为外层循环遍历节点与被处理元素的对照组,初始值:head。
第二个节点作为被处理元素的前驱节点,初始值也:第一个节点。
第三个节点作为被处理元素,初始值为:第二个节点->next。
具体实现的看代码细节:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode* removeDuplicateNodes(ListNode* head) {if(head == nullptr) return head;ListNode* pos = head; //对照节点while(pos != nullptr){ListNode* pre = pos; //被处理元素的前驱节点ListNode* cur = pre->next; //被处理元素while(cur != nullptr){if(pos->val != cur->val){pre = cur;}else{pre->next = cur->next;}cur = cur->next;}pos = pos->next;}return head;}
};
复杂度分析:
时间复杂度O(N^2),其中N代表所给链表的节点数。用了两个while循环。
空间复杂度O(1),因为只用到了几个临时变量。
优化:双层遍历法
这次代码对应上次的优化是只设置了两个节点用来变量。我们将pos作为外层遍历节点与对照组节点,将cur作为前驱节点,将cur->next作为被处理节点。
减少了一个临时变量的设置,优化了一行代码,但是代码的易读性变差,并且代码易错性增强。
具体实现看代码:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode* removeDuplicateNodes(ListNode* head) {if(head == nullptr) return head;ListNode* pos = head; while(pos != nullptr){ListNode* cur = pos; while(cur->next != nullptr){ if(cur->next->val == pos->val)cur->next = cur->next->next; elsecur = cur->next;}pos = pos->next;}return head;}
};
复杂度分析:
时间复杂度O(N^2),其中N代表所给链表的节点数。用了两个while循环。
空间复杂度O(1),因为只用到了几个临时变量。
相关文章:
》面试题 02.01. 移除重复节点)
《程序员面试金典(第6版)》面试题 02.01. 移除重复节点
题目描述 编写代码,移除未排序链表中的重复节点。保留最开始出现的节点。 示例1: 输入:[1, 2, 3, 3, 2, 1] 输出:[1, 2, 3] -示例2: 输入:[1, 1, 1, 1, 2] 输出:[1, 2] 提示: 链表长度在[0, 20000]范…...
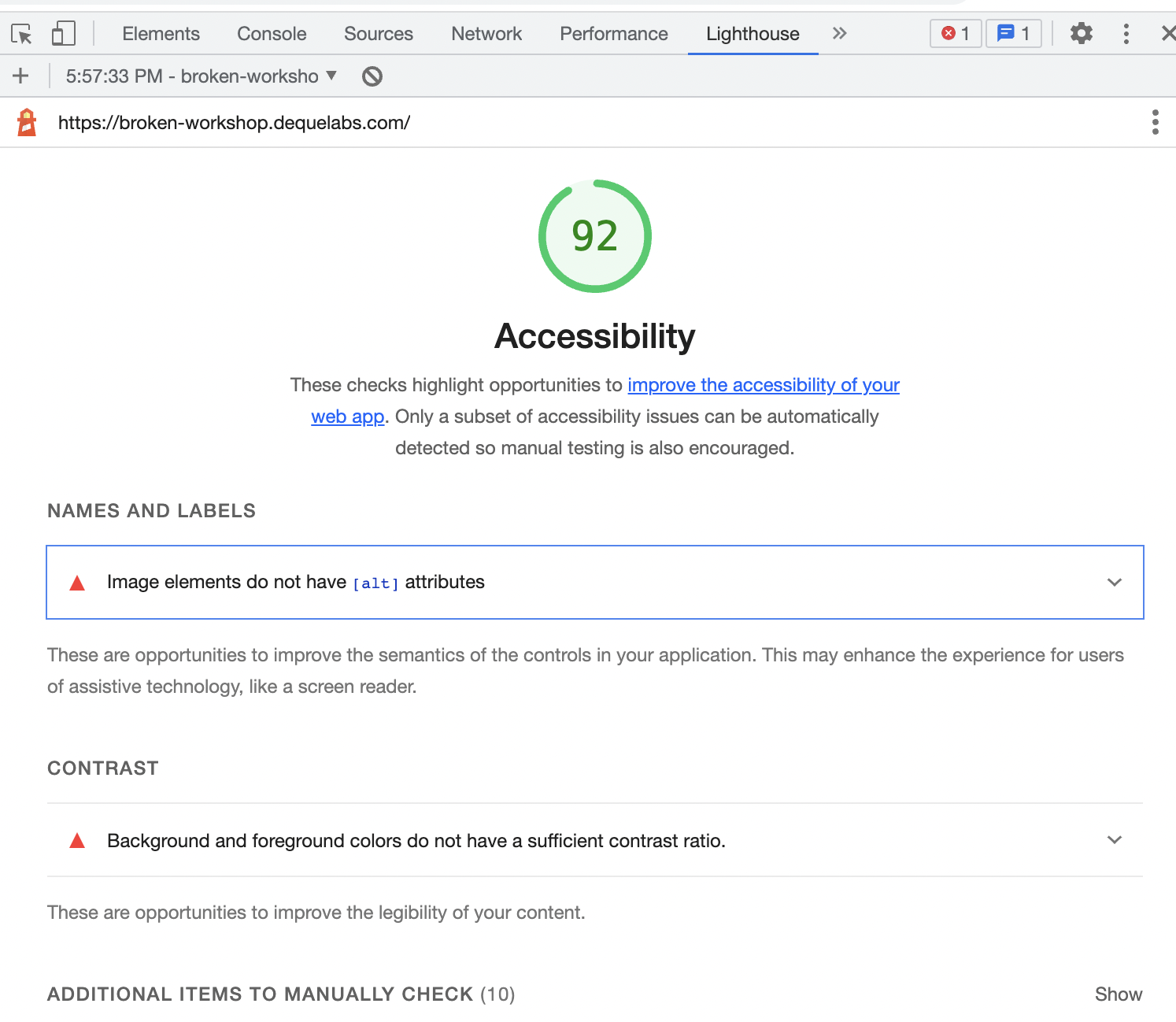
如何对web系统开展无障碍测试
Accessibility test(无障碍测试)是一种测试方法,旨在评估软件、网站或其他数字产品的可访问性,以确保它们能够被身体残障或其他特殊需求的用户使用。这些测试通常包括使用辅助技术,如屏幕阅读器和放大器,以…...

使用vite+vue3.0 创建一个cesium基础应用 ----01 项目搭建
使用vitevue3.0 创建一个cesium基础应用 ----01 项目搭建 1.使用yarn创建一个vite项目 我们可以在vite官网找到vite创建项目的命令 https://cn.vitejs.dev/ 可以使用yarn创建项目选择使用vue3.0框架,语言使用js 创建完成后结构如下: 2.找到vite社区中的…...
【Python学习笔记】第二十七节 Python 多线程
一、进程和线程进程:是程序的一次执行,每个进程都有自己的地址空间、内存、数据栈及其他记录运行轨迹的辅助数据。线程:所有的线程都运行在同一个进程当中,共享相同的运行环境。线程有开始、顺序执行和结束三个部分, …...

【id:18】【20分】B. DS顺序表--连续操作
题目描述建立顺序表的类,属性包括:数组、实际长度、最大长度(设定为1000)该类具有以下成员函数:构造函数:实现顺序表的初始化。插入多个数据的multiinsert(int i, int n, int item[])函数,实现在…...
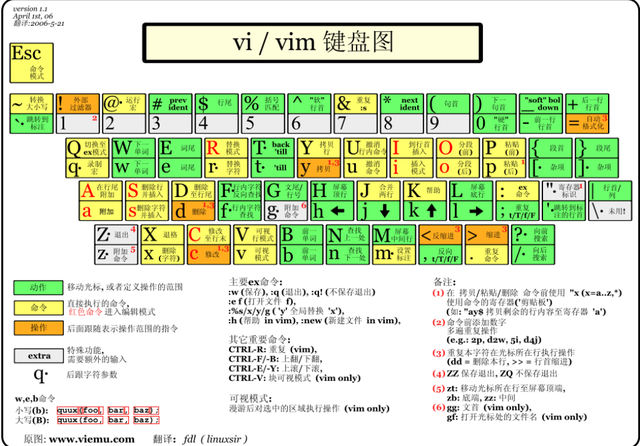
vi编辑器操作指令分享
vi编辑器是所有Unix及Linux系统下标准的编辑器,它的强大不逊色于任何最新的文本编辑器,这里只是简单地介绍一下它的用法和一小部分指令。由于对Unix及Linux系统的任何版本,vi编辑器是完全相同的,因此您可以在其他任何介绍vi的地方…...

OSPF与BFD联动配置
13.1.1BFD概念 BFD提供了一个通用的、标准化的、介质无关的、协议无关的快速故障检测机制,有以下两大优点: 对相邻转发引擎之间的通道提供轻负荷、快速故障检测。 用单一的机制对任何介质、任何协议层进行实时检测。 BFD是一个简单的“Hello”协议。两个系统之间建立BFD会…...

jQuery基础
> 🥲 🥸 🤌 🫀 🫁 🥷 🐻❄️🦤 🪶 🦭 🪲 🪳 🪰 🪱 🪴 🫐 🫒 …...

day39|139.单词拆分 背包问题ending
139.单词拆分 给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。 注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。 示例 1: 输入: s "leetcode",…...

Shell脚本编程
Shell编程 视频地址https://www.bilibili.com/video/BV1hW41167NW/?p1&vd_source977d52a6b92ce8b6ae67c16fc61f0428 第一章 Shell概述 大数据程序员为什么要学习Shell呢? 需要看懂运维人员编写的Shell程序偶尔会编写一些简单的Shell程序来管理集群…...
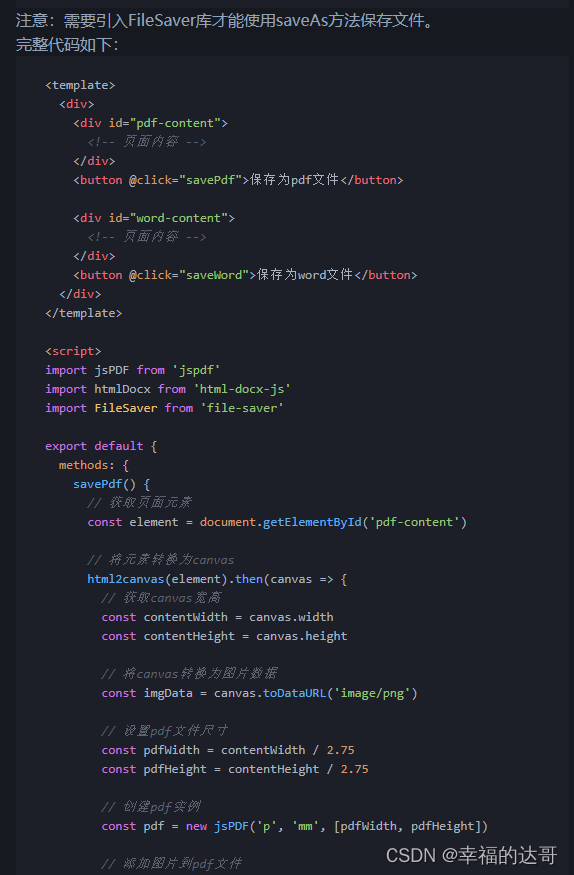
ChatGPT解答:JavaScript保存当前网页页面图片为pdf文件或者word文件,前端用vue2,给出详细的方案和代码
ChatGPT解答:JavaScript保存当前网页页面图片为pdf文件或者word文件,前端用vue2,给出详细的方案和代码 ChatGPTDemo Based on OpenAI API (gpt-3.5-turbo). JavaScript保存当前网页页面图片为pdf文件或者word文件,前端用vue2&am…...

Python基础学习11——文件
我们可以利用python对本电脑文件夹里的文件进行处理,python中提供了一系列相关的方法和函数供我们使用。 读取文件 我们现在在本python文件中有一个txt文件名为Lego,那么我们就可以利用python打开该文件 with open(Lego.txt) as file_text:contents …...
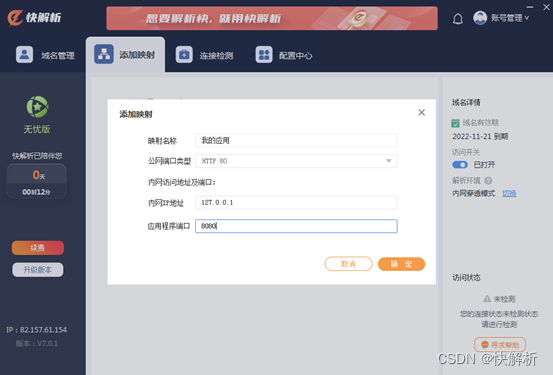
外网用户打不开公司的网站?web服务器端口映射到公网
我们经常会遇到这样的情景,在公司内部可以打开公司的网站,在家里或者外网却打不开,按照网上的做法,重新启动了服务器和iis,还是不行。许多用户设置了路由器端口映射功能,但是端口映射不成功怎么办ÿ…...

【CS224W】(task9)图神经网络的表示能力(更新中!!)
note 基于图同构网络(GIN)的图表征网络。为了得到图表征首先需要做节点表征,然后做图读出。GIN中节点表征的计算遵循WL Test算法中节点标签的更新方法,因此它的上界是WL Test算法。 在图读出中,我们对所有的节点表征&…...
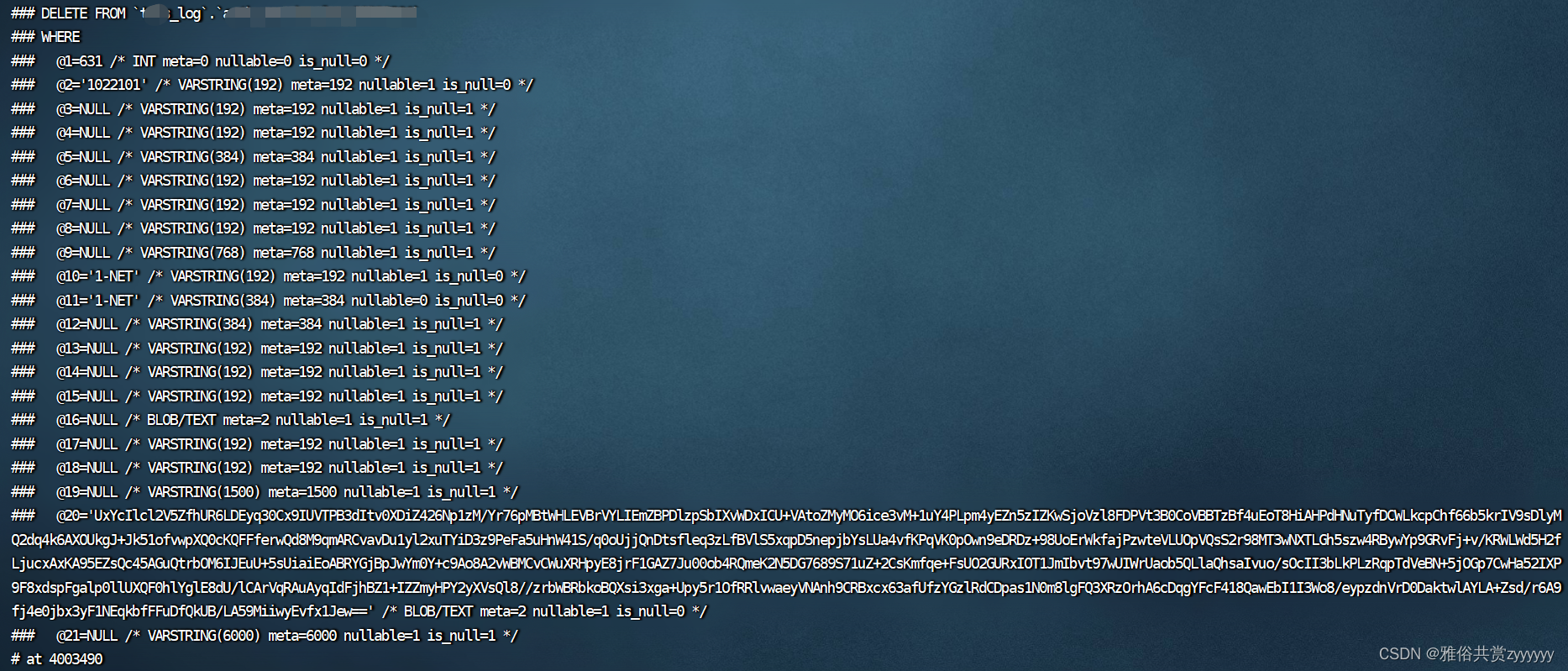
binlog找回误删数据
1、检查当前是否开启binlog存储 输入命令show variables like %log_bin%;,结果如下 可以看到log_bin的值是ON,说明binlog开启了。 2、查找binlog的存储位置 这个去到数据库的my.cnf配置文件中寻找,有一个log_bin的配置 切换到log_bin的目…...
》面试题 02.03. 删除中间节点)
《程序员面试金典(第6版)》面试题 02.03. 删除中间节点
题目描述 若链表中的某个节点,既不是链表头节点,也不是链表尾节点,则称其为该链表的「中间节点」。 假定已知链表的某一个中间节点,请实现一种算法,将该节点从链表中删除。 例如: 传入节点 c(…...
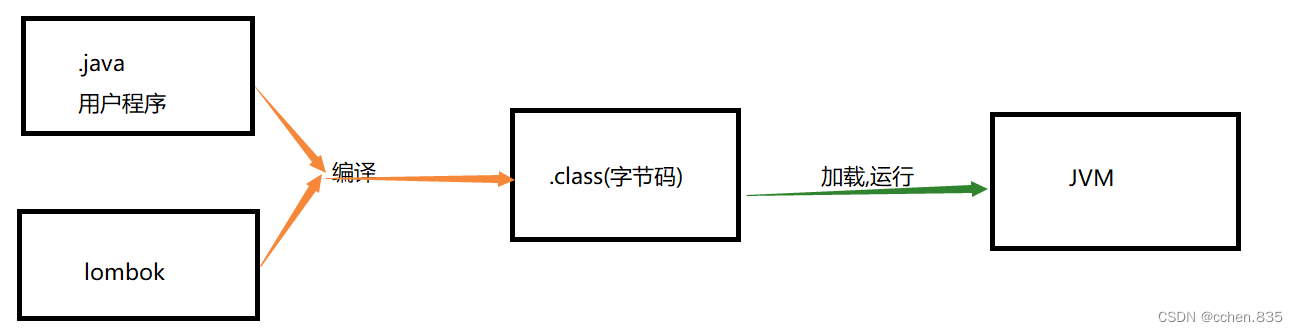
Spring Boot
目录 SpringBoot SpringBoot创建和使用 什么是Spring Boot Spring Boot优点 Spring Boot项目的创建 项目目录介绍和运行 目录介绍 项目运行 SpringBoot核心设计思想 SpringBoot的配置文件 配置文件的作用 配置文件的格式 注意事项 properties配置文件 propertie…...
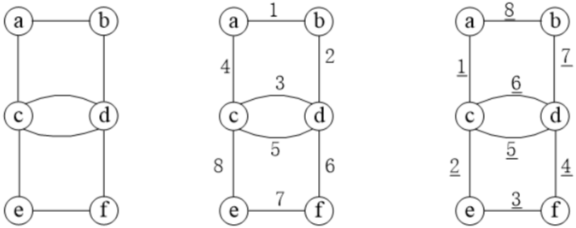
图论初入门
目录 一、前言 二、图的概念 三、例题及相关概念 1、全球变暖(2018年省赛,lanqiao0J题号178) 2、欧拉路径 3、小例题 4、例题(洛谷P7771) 一、前言 本文主要讲了树与图的基本概念,图的存储、DFS遍历…...

02-Oracle数据库的启动与关闭
本文章主要讲解Oracle数据库的启动与关闭方法,详细讲解启动Oracle的命令,三种启动数据库的方法及区别;关闭数据库的4种方法及他们的区别。 启动和关闭数据库 •数据库没启动前,只有拥有DBA权限或者以sysoper或sysdba身份才能连接到…...

网络营销培训完能达到什么水平?学完能创业吗?
网络营销本身就是一门创业的技术,很多人学习网络营销,往往担心学完以后技术达不到,再工作几年才可以创业,实际这是错误的理解,那么,网络营销培训完能达到什么水平?新手学员参加网络营销培训&…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...
