传感数据分析中的小波滤波:理论与公式
传感数据分析中的小波滤波:理论与公式
引言
在传感数据分析领域,小波滤波作为一种强大的信号处理工具,广泛应用于噪声去除、信号压缩、特征提取以及频谱分析等方面。本文将深入介绍小波滤波的理论基础和相关数学公式,以更全面地理解和应用这一先进的数据分析技术。
一、小波变换基础
小波变换是一种多尺度分析方法,它能够提供信号在时间和频率上的局部信息。小波叶滤波的核心是小波变换,其中包括连续小波变换(CWT)和离散小波变换(DWT)。
1. 连续小波变换(CWT)
连续小波变换的基本公式为:
W ( a , b ) = ∫ − ∞ ∞ x ( t ) ⋅ ψ ( t − b a ) d t \begin{equation}W(a, b) = \int_{-\infty}^{\infty} x(t) \cdot \psi\left(\frac{t - b}{a}\right) \, dt \end{equation} W(a,b)=∫−∞∞x(t)⋅ψ(at−b)dt
其中, W ( a , b ) W(a, b) W(a,b)是小波系数, x ( t ) x(t) x(t)是原始信号, ψ ( t ) \psi(t) ψ(t) 是小波基函数, a a a是尺度参数, b b b 是平移参数。
2. 离散小波变换(DWT)
离散小波变换通过迭代地进行信号分解和重构,是实际应用中更为常见的形式。DWT的基本公式为:
W ( j , k ) = ⟨ x , ψ j , k ⟩ = ∫ − ∞ ∞ x ( t ) ⋅ ψ j , k ( t ) d t \begin{equation}W(j, k) = \langle x, \psi_{j, k} \rangle = \int_{-\infty}^{\infty} x(t) \cdot \psi_{j, k}(t) \, dt \end{equation} W(j,k)=⟨x,ψj,k⟩=∫−∞∞x(t)⋅ψj,k(t)dt
其中, W ( j , k ) W(j, k) W(j,k)是离散小波系数, ψ j , k ( t ) \psi_{j, k}(t) ψj,k(t)是小波基函数。
二、小波滤波原理
小波通过选择适当的小波基函数和尺度参数,实现对信号的多尺度分解和重构。常见的小波基函数有 Haar、Daubechies、Symlet 等,它们具有不同的频率特性和支持范围。
小波滤波的级数分解和重构公式为:
x ( t ) = ∑ j = 0 J − 1 ∑ k W j , k ⋅ ψ j , k ( t ) \begin{equation} x(t) = \sum_{j=0}^{J-1} \sum_{k} W_{j, k} \cdot \psi_{j, k}(t) \end{equation} x(t)=j=0∑J−1k∑Wj,k⋅ψj,k(t)
其中, J J J是分解的级数, W j , k W_{j, k} Wj,k是第 j j j级、第 k k k个小波系数。
三、小波叶滤波的应用
小波滤波在传感数据分析中有着广泛的应用,具有以下特点:
- 多尺度分析: 小波滤波能够捕捉信号在不同尺度上的变化,适用于非平稳信号的分析。
- 局部特征提取: 小波滤波可以突出信号的局部特征,有助于精确提取信号中的重要信息。
- 时频局部性: 与傅里叶变换不同,小波滤波具有时频局部性,更适用于分析具有瞬时频率变化的信号。
四、小波叶滤波的具体例子
让我们通过一个具体的例子来演示小波叶滤波的应用。考虑一个包含高频和低频成分的信号,我们将使用小波叶滤波进行分解和重构,观察其效果。
import pywt
import numpy as np
import matplotlib.pyplot as plt# 生成信号
t = np.linspace(0, 1, 1000, endpoint=False)
signal = np.sin(2 * np.pi * 20 * t) + 0.5 * np.sin(2 * np.pi * 5 * t)# 进行小波分解
coeffs = pywt.wavedec(signal, 'db1', level=4)# 设置部分小波系数为零,实现信号压缩
coeffs[1:] = (pywt.threshold(c, 0.1, mode='soft') for c in coeffs[1:])# 进行小波重构
reconstructed_signal = pywt.waverec(coeffs, 'db1')# 可视化结果
plt.figure(figsize=(10, 6))plt.subplot(2, 1, 1)
plt.plot(t, signal, label='Original Signal')
plt.legend()plt.subplot(2, 1, 2)
plt.plot(t, reconstructed_signal, label='Reconstructed Signal', color='red')
plt.legend()plt.show()
结论
小波滤波作为传感数据分析中的重要工具,通过灵活选择小波基函数和尺度参数,实现了对非平稳信号的高效分解和重构。本文介绍了小波变换的基础理论和小波滤波的相关公式,希望读者通过学习和实践能够更好地应用这一强大的数据分析技术,提升对传感数据的处理能力。
后续将持续对传感数据分析领域的各种理论进行分析。
相关文章:

传感数据分析中的小波滤波:理论与公式
传感数据分析中的小波滤波:理论与公式 引言 在传感数据分析领域,小波滤波作为一种强大的信号处理工具,广泛应用于噪声去除、信号压缩、特征提取以及频谱分析等方面。本文将深入介绍小波滤波的理论基础和相关数学公式,以更全面地…...

iOS 按钮添加点击震动
1. 方法说明: iOS10后系统提供了一套API来简单实现震动: init时传入一个style定义好的枚举就可以实现不同的震动 typedef NS_ENUM(NSInteger, UIImpactFeedbackStyle) {UIImpactFeedbackStyleLight,UIImpactFeedbackStyleMedium,UIImpactFeedbackStyle…...
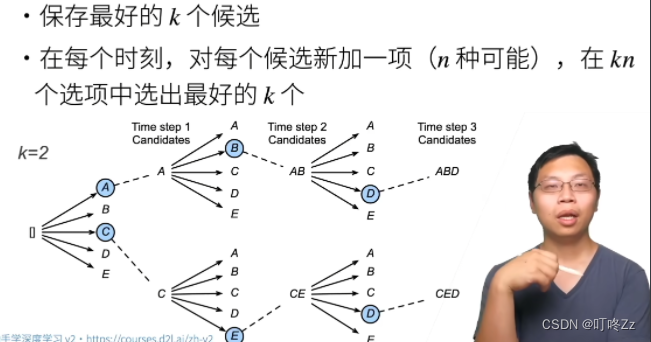
李沐-《动手学深度学习》--02-目标检测
一 、目标检测算法 1. R-CNN a . 算法步骤 使用启发式搜索算法来选择锚框(选出多个锚框大小可能不一,需要使用Rol pooling)使用预训练好的模型(去掉分类层)对每个锚框进行特征抽取(如VGG,AlexNet…)训练…...
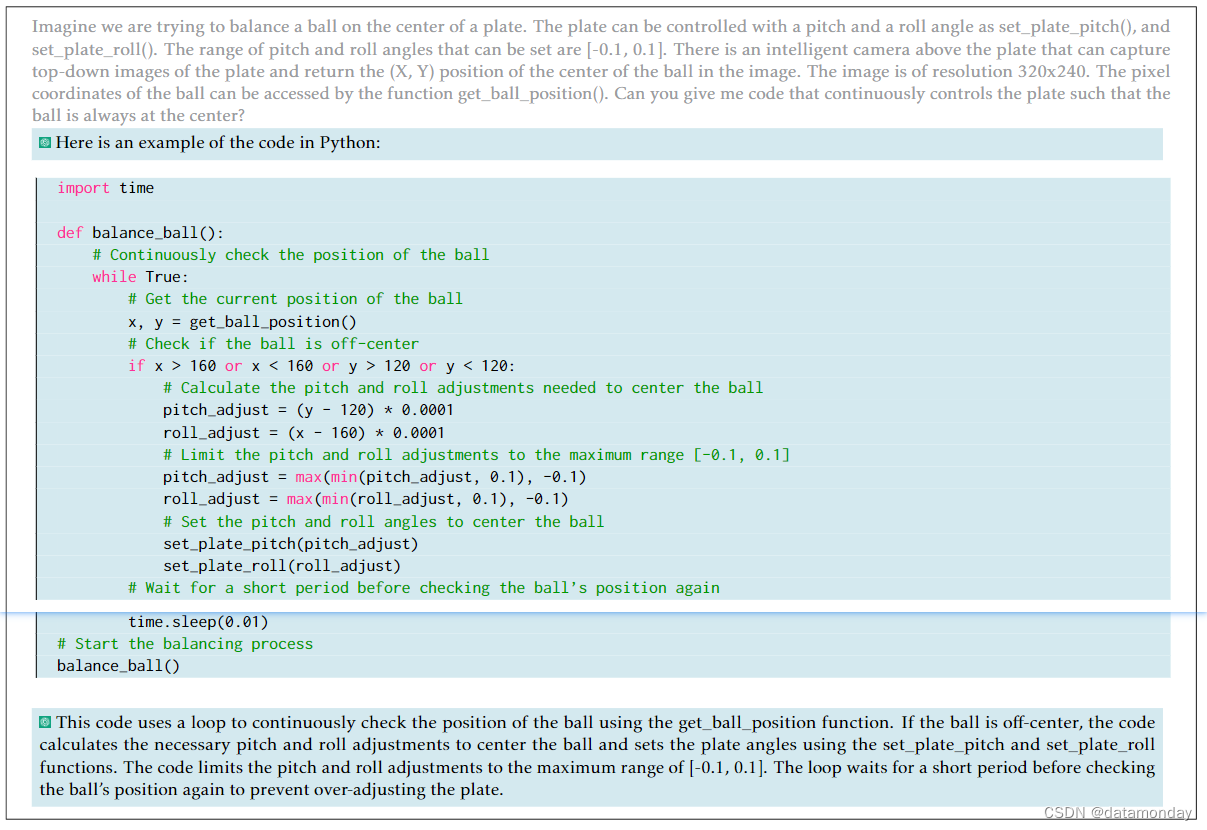
【EAI 006】ChatGPT for Robotics:将 ChatGPT 应用于机器人任务的提示词工程研究
论文标题:ChatGPT for Robotics: Design Principles and Model Abilities 论文作者:Sai Vemprala, Rogerio Bonatti, Arthur Bucker, Ashish Kapoor 作者单位:Scaled Foundations, Microsoft Autonomous Systems and Robotics Research 论文原…...

.pings勒索病毒的威胁:如何应对.pings勒索病毒的突袭?
引言: 在网络安全领域,.pings勒索病毒一直是不断演变的威胁之一。其变种的不断出现使得对抗这一数字威胁变得更加复杂。本节将深入剖析.pings勒索病毒变种的出现,以更好地理解其威胁性质和对策。如果受感染的数据确实有恢复的价值与必要性&a…...
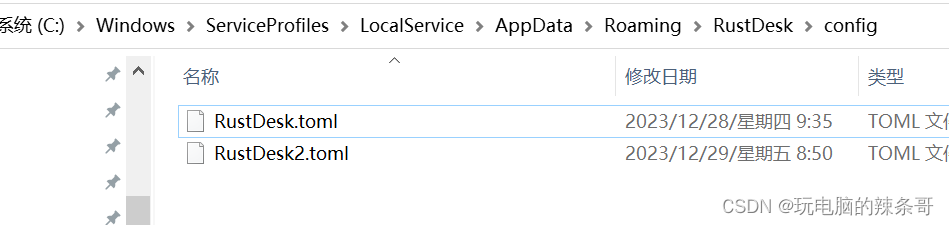
Rustdesk本地配置文件存在什么地方?
环境: rustdesk1.1.9 Win10 专业版 问题描述: Rustdesk本地配置文件存在什么地方? 解决方案: RustDesk 是一款功能齐全的远程桌面应用。 支持 Windows、macOS、Linux、iOS、Android、Web 等多个平台。 支持 VP8 / VP9 / AV1 …...
36-javascript输出方式,弹框:普通,confirm弹框,prompt弹框,控制台输出:普通,warm,error
1.页面打印 <body><p>你真是一个小机灵鬼</p><script>// 页面打印document.write("打印内容");</script> </body> 2.覆盖文档 <body><p>你真是一个小机灵鬼</p><script>// 覆盖文档window.onload f…...

自动执行 Active Directory 清理
Active Directory (AD) 可帮助 IT 管理员分层存储组织的资源,包括用户、组以及计算机和打印机等设备,这有助于管理员集中创建基于帐户和组的规则,并通过创建不合规的自动日志来强制执行和确保合规性。 不时清理AD是保…...
DICE模型的原理与推导、碳循环与气候变化、政策评估、不确定性分析与代码分析
目录 专题一:DICE模型的原理与推导 专题二:碳循环与气候变化 专题三:政策评估 专题四:不确定性分析与代码分析 更多应用 随着温室气体排放量的增大和温室效应的增强,全球气候变化问题受到日益的关注。我国政府庄严…...

【机器学习前置知识】狄利克雷分布
在阅读本文前,建议先食用以下几篇文章以能更好地理解狄利克雷分布: 二项分布 Beta分布 多项分布 共轭分布 狄利克雷分布 狄利克雷分布(Dirichlet distribution)是Beta分布的扩展,把Beta分布从二元扩展到多元形式就是狄利克雷分布&#…...
)
Spring Retry(方法重试、方法重新调用)
Spring Retry——方法重试、方法重新调用 简介:使用1. 配置2.使用 总结注意 简介: Spring Retry 是一个 Spring Boot 官方提供的支持重试机制的库。它提供了一种简单而灵活的方式来处理方法调用可能失败的情况,通过自动重试失败的操作&#…...

JavaScript音视频,使用JavaScript如何在浏览器录制电脑摄像头画面为MP4视频文件并下载视频文件到本地
前言 本章介绍使用JavaScript如何在浏览器录制电脑摄像头画面为MP4视频文件并下载视频文件到本地。 实现功能 1、使用navigator.mediaDevices.getUserMedia获取摄像头画面 2、将获取到的摄像头画面渲染到canvas画板上 3、将canvas转换为blob对象 4、通过document.createElem…...

IaC基础设施即代码:使用Terraform 连接 alicloud阿里云
目录 一、实验 1.环境 2.alicloud阿里云创建用户 3.Linux使用Terraform 连接 alicloud 4.Windows使用Terraform 连接 alicloud 二、问题 1.Windows如何申明RAM 相关变量 2.Linux如何申明RAM 相关变量 3. Linux terraform 初始化失败 4.Linux terraform 计划与预览失败…...

Vue3 如何使用移动端调试工具vConsole
1、安装 pnpm i vconsole2、在src/utils下新建vconsole.ts,写入以下代码 // 这是移动端控制台调试工具,需要调试就打开,不用就注释 import vConsole from vconsole const vconsole new vConsole()3、src/main.ts 引入,需要调试就打开,&…...

【物流管理系统-Python简易版】
前端设计-后端开发(DJango项目Demo) 参考资料:【一文到底】【0基础】【快速上手】Django基本使用 创建项目 Pycharm专业版新建DJango项目 项目文件介绍: django_study_demo │─ manage.py 【项目管理的脚本,不要修…...

Vue学习笔记六--Vue3学习
1、Vue3的优势 2、创建Vue3工程 前提:node -v 查看node版本,需要在16.0及以上 创建命令 npm init vuelatest,先安装create-vue然后创建项目 然后执行npm run dev 提示 sh: vite: command not found,需要执行npm i重新安装依赖,之后再执行np…...

21.在线与离线MC强化学习简介
文章目录 1. 什么是在线MC强化学习2. 什么是离线MC强化学习3. 在线MC强化学习有何缺点 1. 什么是在线MC强化学习 在线强化学习(on-policy MC RL),是指:智能体在策略评估时为获取完整轨迹所采用的采样策略 π s a m p l e ( a ∣ …...

控制网页的灰度显示
1.代码: 普通网页 <style>html {filter: grayscale(100%);}</style> 或是:webkit内核浏览器写法 <style>html {-webkit-filter: grayscale(100%)}</style> 2.说明: grayscale(amount) :进行灰度转换。 amount转换值的大小&…...
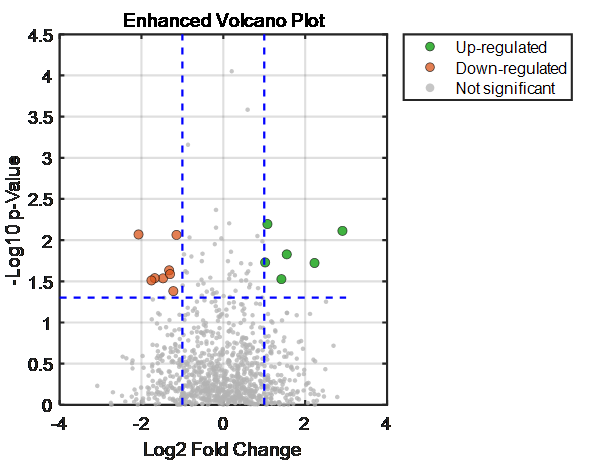
科研绘图(四)火山图
火山图是生物信息学中常用的一种图表,用来显示基因表达数据的变化。它通常将每个点表示为一个基因,x轴显示对数比率(log ratio),表示基因表达的变化大小;y轴显示-log10(p-value),表示变化的统计…...
超强站群系统v9.0:最新蜘蛛池优化技术,一键安装,内容无缓存刷新,高效安全
安全、高效,化的优化利用php性能,使得运行流畅稳定 独创内容无缓存刷新不变,节省硬盘。防止搜索引擎识别蜘蛛池 蜘蛛池算法,轻松构建站点(电影、资讯、图片、论坛等等) 可以个性化每个网站的风格、内容、…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...
