蓝桥杯AcWing学习笔记 8-2数论的学习(下)
蓝桥杯
我的AcWing
题目及图片来自蓝桥杯C++ AB组辅导课
数论(下)
蓝桥杯省赛中考的数论不是很多,这里讲几个蓝桥杯常考的知识点。
约数个数定理
我们如何去求一个数的约数个数呢?
N N N分解质因数的结果: N = P 1 α 1 × P 2 α 2 × . . . × P k α k N=P_{1}^{α_{1}}×P_{2}^{α_{2}}×...×P_{k}^{α_{k}} N=P1α1×P2α2×...×Pkαk
约数个数是: ( α 1 + 1 ) ( α 2 + 1 ) . . . ( α k + 1 ) (α_{1}+1)(α_{2}+1)...(α_{k}+1) (α1+1)(α2+1)...(αk+1)
假设 N N N的一个约数 d = P 1 β 1 × P 2 β 2 × . . . × P k β k ( 0 ≤ β i ≤ α i ) d=P_{1}^{β_{1}}×P_{2}^{β_{2}}×...×P_{k}^{β_{k}}(0 \leq β_{i}\leq α_{i}) d=P1β1×P2β2×...×Pkβk(0≤βi≤αi),每一个约数都可以表示为这样的形式,这种约数的个数也就等于 k k k 元组的个数: ( β 1 , β 2 . . . β k ) (β_{1},β_{2}...β_{k}) (β1,β2...βk),这 k k k 元组有多少种选法: ( α 1 + 1 ) ⋅ ( α 2 + 1 ) ⋅ ( α k + 1 ) (α_{1}+1)·(α_{2}+1)·(α_{k}+1) (α1+1)⋅(α2+1)⋅(αk+1)
约数和定理
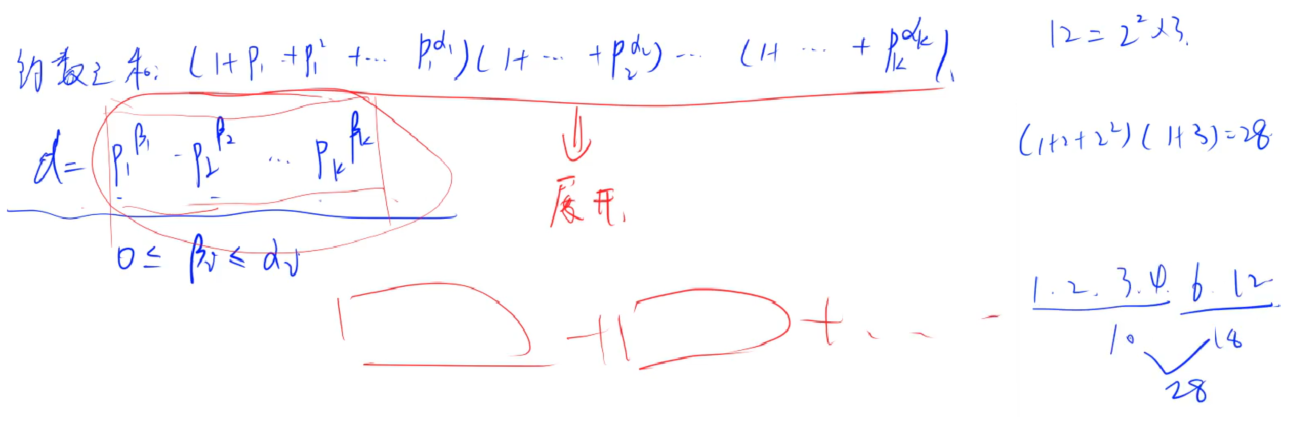
公式: ( 1 + P 1 + P 1 2 + . . + P 1 α 1 ) ( 1 + P 2 + P 2 2 + . . + P 2 α 2 ) . . . ( 1 + P k + P k 2 + . . + P k α k ) (1+P_{1}+P_{1}^2+..+P_{1}^{α_{1}})(1+P_{2}+P_{2}^2+..+P_{2}^{α_{2}})...(1+P_{k}+P_{k}^2+..+P_{k}^{α_{k}}) (1+P1+P12+..+P1α1)(1+P2+P22+..+P2α2)...(1+Pk+Pk2+..+Pkαk)
这个公式展开了就是上面定理的约数 d = P 1 β 1 × P 2 β 2 × . . . × P k β k ( 0 ≤ β i ≤ α i ) d=P_{1}^{β_{1}}×P_{2}^{β_{2}}×...×P_{k}^{β_{k}}(0 \leq β_{i}\leq α_{i}) d=P1β1×P2β2×...×Pkβk(0≤βi≤αi) 之和。
例题
AcWing 1296. 聪明的燕姿
约数个数定理
约数和定理
给我们一个 S S S,问我们有多少个正整数满足它的所有正约数之和等于 S S S。
S S S 满足约数和定理: S = ( 1 + P 1 + P 1 2 + . . + P 1 α 1 ) ( 1 + P 2 + P 2 2 + . . + P 2 α 2 ) . . . ( 1 + P k + P k 2 + . . + P k α k ) S=(1+P_{1}+P_{1}^2+..+P_{1}^{α_{1}})(1+P_{2}+P_{2}^2+..+P_{2}^{α_{2}})...(1+P_{k}+P_{k}^2+..+P_{k}^{α_{k}}) S=(1+P1+P12+..+P1α1)(1+P2+P22+..+P2α2)...(1+Pk+Pk2+..+Pkαk)
因为方案数非常少,我们可以用暴搜dfs求解。
这题太难理解啦,之后的题也没有做了。
相关文章:

蓝桥杯AcWing学习笔记 8-2数论的学习(下)
蓝桥杯 我的AcWing 题目及图片来自蓝桥杯C AB组辅导课 数论(下) 蓝桥杯省赛中考的数论不是很多,这里讲几个蓝桥杯常考的知识点。 约数个数定理 我们如何去求一个数的约数个数呢? N N N分解质因数的结果: N P 1 α…...
vcs makefile
主要参考: VCS使用Makefile教程_vcs makefile-CSDN博客https://blog.csdn.net/weixin_45243340/article/details/129255218?ops_request_misc%257B%2522request%255Fid%2522%253A%2522170524049516800227431373%2522%252C%2522scm%2522%253A%252220140713.1301023…...
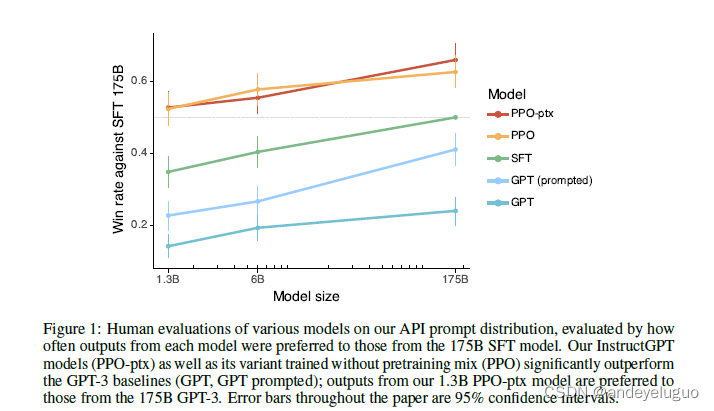
《Training language models to follow instructions》论文解读--训练语言模型遵循人类反馈的指令
目录 1摘要 2介绍 方法及实验细节 3.1高层次方法论 3.2数据集 3.3任务 3.4人体数据收集 3.5模型 3.6评价 4 结果 4.1 API分布结果 4.2公共NLP数据集的结果 4.3定性结果 问题 1.什么是rm分数 更多资料 1摘要 使语言模型更大并不能使它们更好地遵循用户的意图。例…...

Redis的实现二: c、c++的网络通信编程技术,让服务器处理多个client
看过上期的都知道,我是搞java的,所以对这些可能理解不是很清楚,各位看完可以尽情发言。 事件循环和非阻塞IO 在服务器端网络编程中,有三种处理并发连接的方法。 它们是:分叉、多线程和事件循环。分叉为每个客户端连接创建新…...
QT上位机开发(动画效果)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 不管是仿真,还是对真实环境的一比一模拟,动画都是非常好的一种呈现方式。目前在qt上面,实现动画主要有两种方法…...

手写实现 bind 函数
Function.prototype.myBind function(context) {if (typeof this ! function) {return}const args [...arguments].slice(1)const fn thisreturn function Fn() {// 判断函数作为构造函数的情况,这个时候需要传入当前的函数的this给apply调用,其余情况…...

安卓Android Studio读写MifareOne M1 IC卡源码
本示例使用的发卡器:https://item.taobao.com/item.htm?id615391857885&spma1z10.5-c-s.w4002-21818769070.11.3d2f789eOUPJBK <?xml version"1.0" encoding"utf-8"?> <androidx.constraintlayout.widget.ConstraintLayout xm…...
一二三应用开发平台文件处理设计与实现系列之5——MinIO技术预研
背景 上篇介绍了文件读写框架设计与实现,同时顺便说明了本地磁盘存储模式的实现模式。 今天来说下基于文件读写框架,如何集成对象存储组件minio,集成之前,需要对minio进行必要的了解,本篇是minio的技术预研。 minio简…...

Native.js是什么
Native.js 是一个开源项目,旨在通过 JavaScript 调用原生 Android API。它的目标是让 JavaScript 开发者能够使用 Android 原生 API,从而在不编写原生代码的情况下构建 Android 应用。 使用 Native.js,开发者可以使用 JavaScript 调用 Andro…...

Vant-ui图片懒加载
核心代码 在你的全局顶部引入和初始化 Vue.use(vant.Lazyload, {loading: /StaticFile/img/jiazai.jpg,error: /StaticFile/img/jiazai.jpg,lazyComponent: false, });//图片懒加载 <img v-lazy"https://img-blog.csdnimg.cn/direct/3d2c8a7e2c0040488a8128c3e381d58…...
创建EasyCodeMybatisCodeHelperPro模板文件用于将数据库表生成前端json文件
在intellij idea中,通过插件EasyCodeMybatisCodeHelperPro,从现有的模板文件中选择一个复制粘贴,然后稍为修改,即可得到一个合适的模板文件。 现在的前端,越来越像后端。TypeScript替代了JavaScript,引入了…...
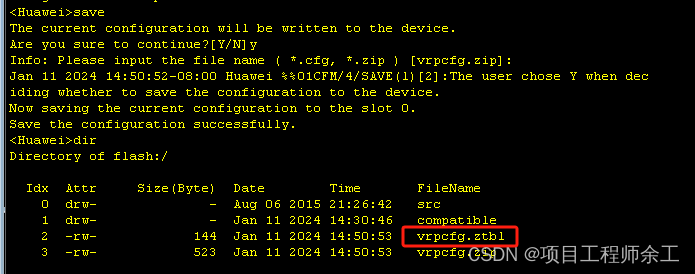
华为端口安全常用3种方法配置案例
安全动态mac地址学习功能 [Huawei]int g0/0/01 interface GigabitEthernet0/0/1 port-security enable //开启安全 port-security max-mac-num 2 //最多为2个mac地址学习 port-security protect-action restrict //丢包带警告 port-security aging-time 1 //mac地址的老化时间…...

RH850P1X芯片学习笔记-Flash Memory
文章目录 FeaturesClock Supply Block DiagramFlash SizeMemory ConfigurationRegistersRegister Base AddressList of RegistersRegister Reset Condition 与Flash Memory相关的操作模式Functional OverviewOption BytesOPBT0 — Option Byte 0OPBT1 — Option Byte 1OPBT2 —…...
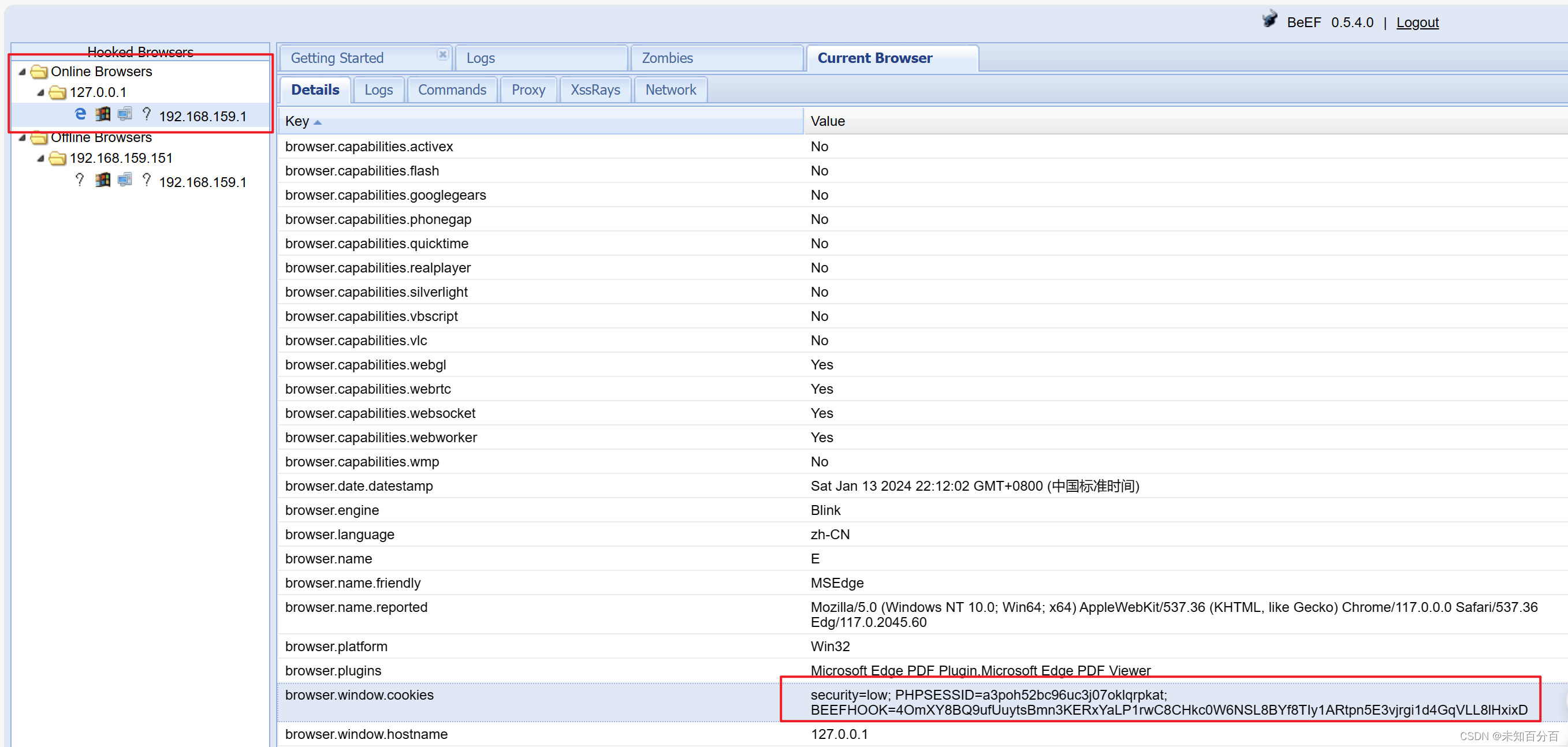
利用XSS漏洞打cookie
目录 1、为什么要打cookie? 2、怎样利用XSS来打cookie? 3、利用Bluelotus_xssReceiver平台来打cookie 4、利用beef-xss平台来打cookie 上一篇给大家介绍了xss漏洞的基础知识,在本篇章将会介绍和演示一下利用xss漏洞打cookie的演示&#x…...

用java写个redis工具类
下面是一个简单的Redis工具类的示例,使用Java语言编写: import redis.clients.jedis.Jedis;public class RedisUtils {private static Jedis jedis;public static void connect(String host, int port) {jedis new Jedis(host, port);}public static v…...

实现防抖函数
// 防抖就是,事件触发 delay 秒后再执行,如果有重新的触发,重新计时 function debounce(func, delay) {if(typeof func ! function) {return}let timer 0return function () {if (timer) {clearTimeout(timer)timer null}timer setTimeout…...

MetaGPT task1学习
基础知识学习了解: 安装环境: 获取MetaGPT 使用pip获取MetaGPT pip install -i https://pypi.tuna.tsinghua.edu.cn/simple metagpt0.5.2 配置MetaGPT 完成MetaGPT后,我们还需要完成一些配置才能开始使用这个强力的框架,包括配…...

关于量子计算机的设想
从CPU架构说起 CISCRISCNISCCCSC CISC是复杂指令集计算机,以x86为代表; RISC是精简指令集计算机,以ARM为代表; NISC是无指令集计算机,CCSC是核-电路分离计算机,这两个是本文要讨论的内容。 如果没有指令…...
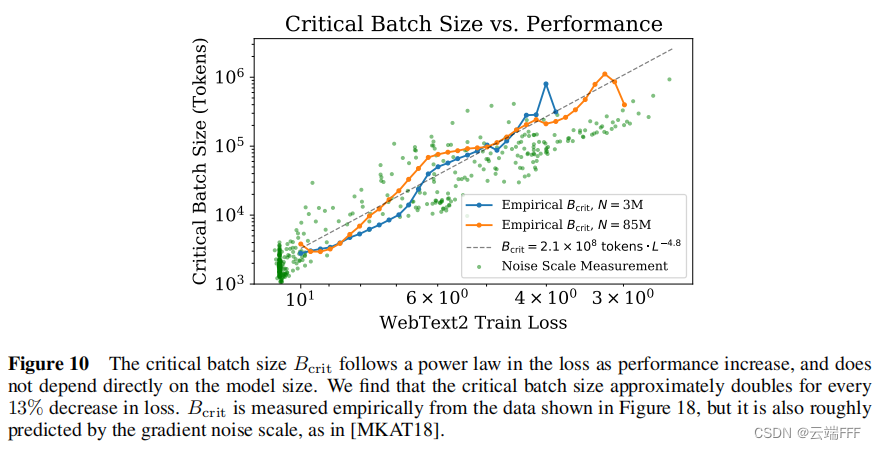
序列模型(4)—— Scaling Laws
本文介绍 LLM 训练过程中重要的 Scaling Laws,这是一个经验规律,指出了固定训练成本(总计算量FLOPs) C C C 时,如何调配模型规模(参数量) N N N 和训练 Token 数据量 D D D,才能实现…...
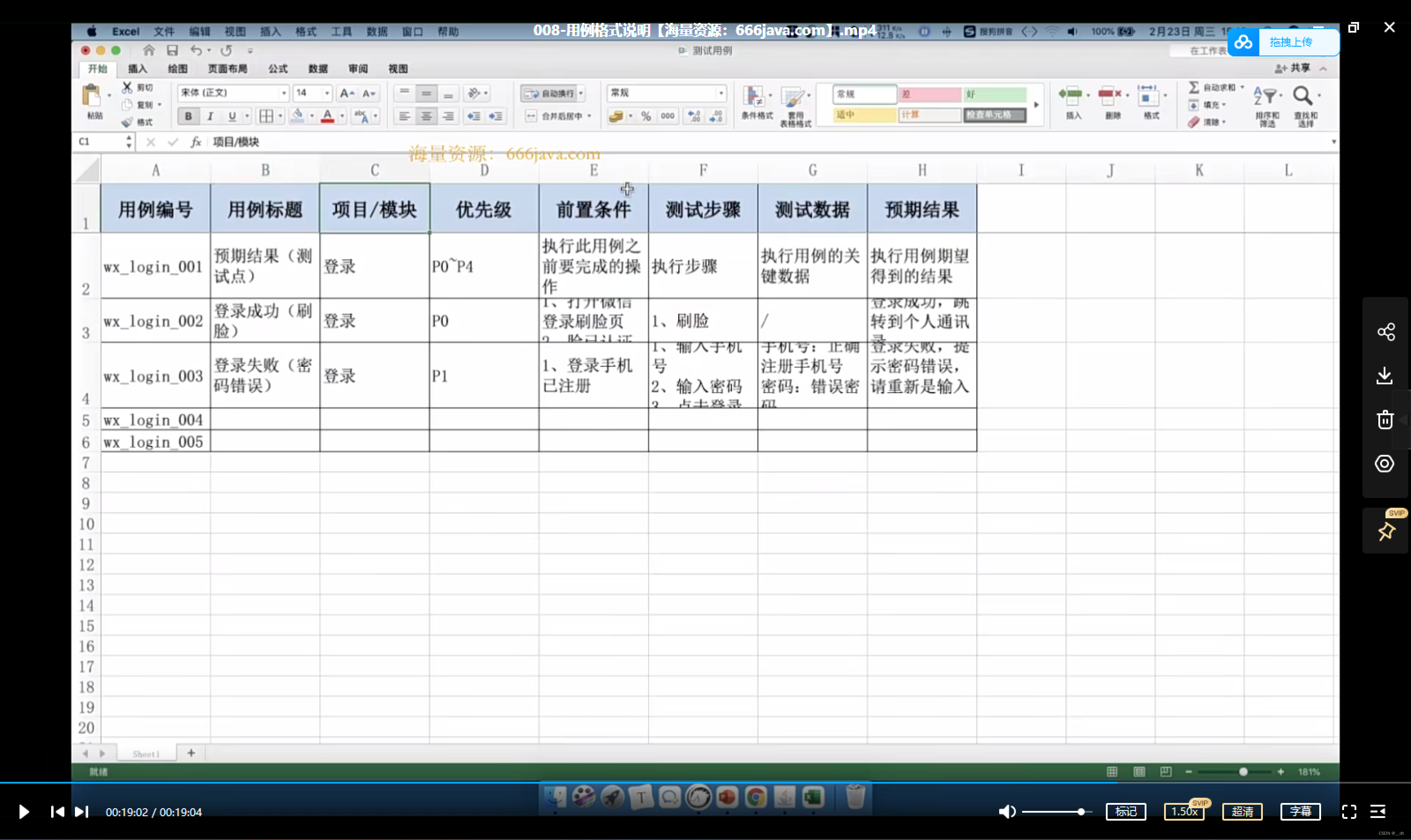
【软件测试学习笔记1】测试基础
1.软件测试的定义 软件的定义:控制计算机硬件工作的工具 软件的基本组成:页面客户端,代码服务器,数据服务器 软件产生的过程:需求产生(产品经理),需求文档,设计效果图…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
