202406读书笔记|《沉睡的线条世界》——翻山越岭，只为与你分享点滴的快乐
《沉睡的线条世界》登登登Dn绘著，简简单单的小画，简简单单的线条，简简单单的语言，温馨又有一点暖心。
怎样的你都好，做最真实的自己。
部分节选如下：
-
愿你我永远有热情，永远能为生活的每一个小惊喜雀跃。
-
我们在夜深人静的时候毫无理由地丧，也许是因为，有一只小可爱在努力。
-
即使是点滴的快乐，我也想跟你分享，哪怕翻山越岭。
-
有期待总是好的
好过你不在出现在我的梦里
想象里
所有的可能不可能的角落。
我总忍不住去期待，
此刻的你是不是也在认真生活，
等待你拥抱我。 -
想送你的人东南西北都顺路！
有人会愿意为你开一艘船，到你的车站接你。 -
我不能保证，明天不会有新的悲伤。我只能给你重新开始的机会，我永远给你重新开始的机会。
对呢，所以要快乐呀
及时行乐！
相关文章：
202406读书笔记|《沉睡的线条世界》——翻山越岭，只为与你分享点滴的快乐
《沉睡的线条世界》登登登Dn绘著，简简单单的小画，简简单单的线条，简简单单的语言，温馨又有一点暖心。 怎样的你都好，做最真实的自己。 部分节选如下： 愿你我永远有热情，永远能为生活的每一个小惊…...
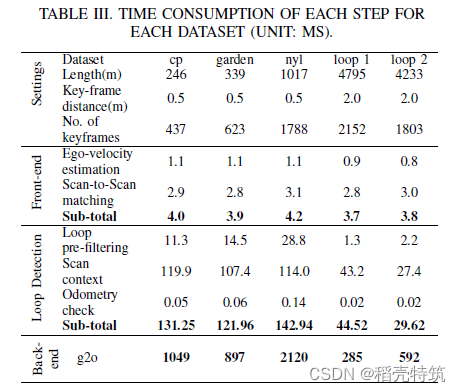
[论文阅读]4DRadarSLAM: A 4D Imaging Radar SLAM System for Large-scale Environments
目录 1.摘要和引言： 2. 系统框架： 2.1 前端： 2.2 回环检测： 2.3 后端： 3.实验和分析： 4.结论 1.摘要和引言： 这篇论文介绍了一种名为“4DRadarSLAM”的新型4D成像雷达SLAM系统࿰…...
Python: vars()详细解释
vars() 是一个内置函数，用于返回一个对象的 __dict__ 属性。它接受一个对象作为参数，如果省略参数，它返回当前局部作用域的字典。 具体而言，vars() 的行为取决于参数的类型： 1. 没有参数： 如果没有提供参…...
2024年1月15日Arxiv最热论文推荐：斯坦福LLM精准微调新框架、GPT不愿承认回答错误、速度快15倍的3D全景分割新突破
本文整理了今日发表在ArXiv上的AI论文中最热门的TOP5。 论文解读、论文热度排序、论文标签、中文标题、推荐理由和论文摘要均由赛博马良平台上的智能体 「AI论文解读达人」提供。 如需查看其他热门论文，欢迎移步赛博马良 ^_^ TOP1 APAR: LLMs Can Do Auto-Paral…...
1.5 面试经典150题 - 轮转数组
轮转数组 给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。 注意：本题需要原地操作 class Solution(object):def rotate(self, nums, k):""":type nums: List[int]:type k: int:rtype: None Do not…...
Linux的基础命令学习
pwd - 显示当前工作目录的路径 cd - 切换工作目录，ls - 列出当前目录的文件和子目录 rm - 删除文件或目录 mkdir - 创建新目录 rm - 删除目录 nano/vi - 编辑文本文件，按Enter键进入 之后按i键就可以进入写入模式 之后输入文字以后按Esc键与:q就不保…...
个人数据备份方案分享（源自一次悲惨经历）
文章目录 1 起源2 备份架构2.1 生活照片2.2 生活录音2.3 微信文件2.4 工作文件2.5 笔记、影视音乐、书籍 3 使用工具介绍3.1 小米云服务3.2 中国移动云盘3.3 小米移动硬盘（1T）3.4 FreeFileSync 4 总结 1 起源 本文的灵感源于我个人的一次不幸遭遇&#…...
 | SpringBoot统一结果封装)
SpringBoot教程(八) | SpringBoot统一结果封装
SpringBoot教程(八) | SpringBoot统一结果封装 经过了前面几篇文章，SpringBoot中MVC相关的配置其实都已经差不多了，接下来就可以完全进入接口开发阶段了。前面我们写过几个接口，虽然都加了RestController注解，相当于统一了我们的…...
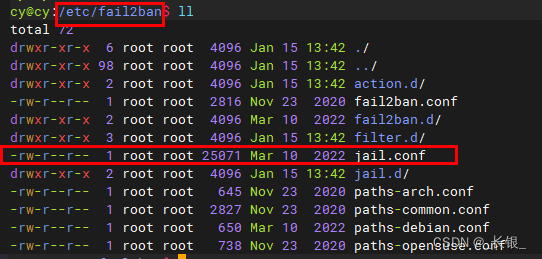
Ubuntu 22.04 安装Fail2Ban
Fail2Ban是一种用来防止暴力破解的工具，一般要和iptables配合使用。其原理是读取系统日志，并通过正则表达式匹配，监控IP在一段时间内的登录尝试、身份验证失败日志等并进行计数。超过阈值则进行IP封禁，过一段时间后再解封。 总的…...
Ubuntu 22.04 编译安装 Qt mysql驱动
参考自 Ubuntu20.04.3 QT5.15.2 MySQL驱动编译 Ubuntu 18.04 编译安装 Qt mysql驱动 下边这篇博客不是主要参考的, 但是似乎解决了我的难题(找不到 libmysqlclient.so) ubuntu18.04.2 LTS 系统关于Qt5.12.3 无法加载mysql驱动，需要重新编译MYSQL数据库驱动的问题以…...
Mindspore 公开课 - CodeGeeX
CodeGeeX: 多语言代码生成模型 CodeGeeX 是一个具有130亿参数的多编程语言代码生成预训练模型。CodeGeeX采用华为MindSpore框架实现，在鹏城实验室“鹏城云脑II”中的192个节点（共1536个国产昇腾910 AI处理器）上训练而成。截至2022年6月22日&…...
说一下mysql的锁
1、全局锁： 影响整个数据库的锁。例如，当执行 FLUSH TABLES WITH READ LOCK; 命令时，会阻止其他用户写入数据库，但可以读取。全局锁简介 全局锁是一种跨所有数据库实例的锁。它可以确保在任何时刻，只有一个事务能够访问共享资源。全局锁通常用于以下场景： 并发性较高的场…...
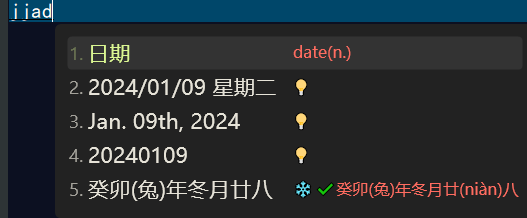
rime中州韵小狼毫 日期/农历 时间 事件 节气 滤镜
教程目录：rime中州韵小狼毫须鼠管安装配置教程 保姆级教程 100增强功能配置教程 网络上但凡提到 rime中州韵小狼毫须鼠管输入法，总少不了智能时间，日期等炫技，可见这个便捷时间/日期输入功能是多么的受欢迎。作者也不落窠臼&…...
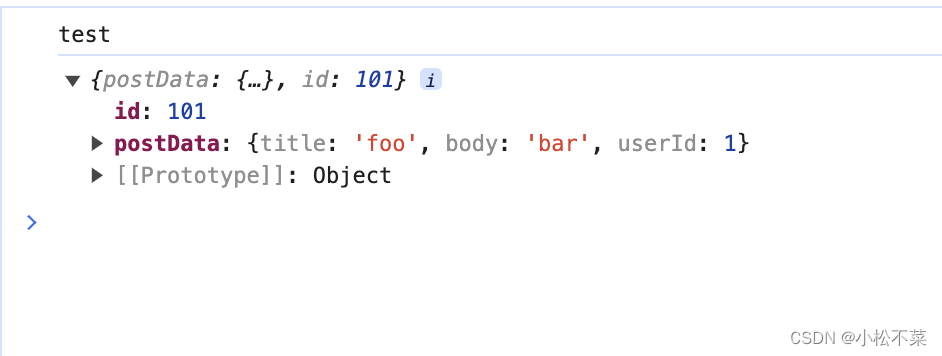
【前端】前后端的网络通信基础操作（原生ajax, axios, fetch）
概述 前后端网络请求工具 原生ajaxfetch apiaxios GET和POST请求 get只能发纯文本 post可以发不同类型的数据，要设置请求头，需要告诉服务器一些额外信息 测试服务器地址 有一些公共的测试 API 可供学习和测试用途。这些 API 允许你发送 HTTP 请求…...
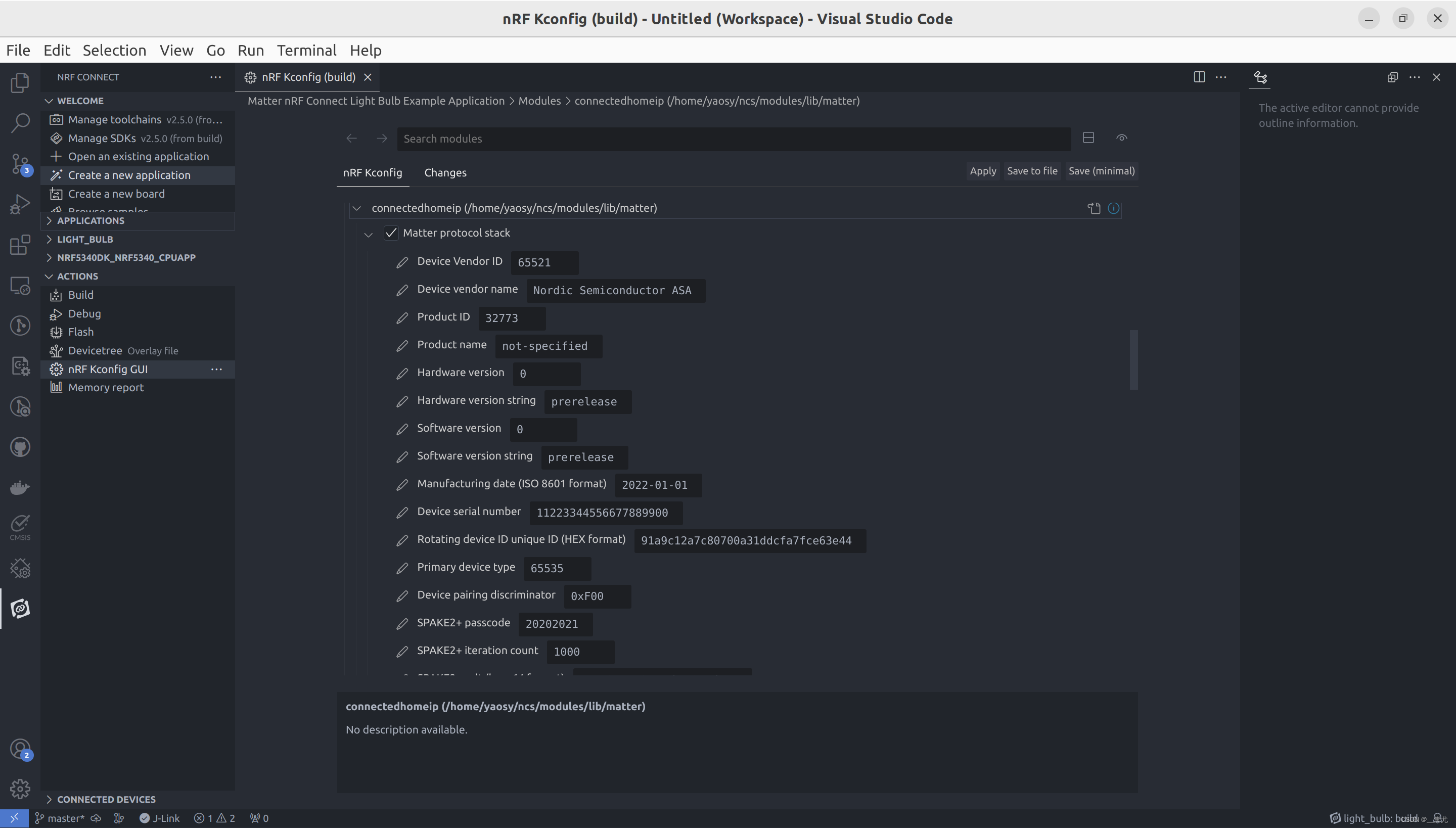
Matter - 配置工厂数据（2）
部分关键名词参数简介 PASE(Passcode-Authenticated Session Establishment): 基于密码认证的会话建立，用于在 Commissioning 的时候 Commissioner 与 Matter Deivce 之间建立安全信道，生成对称加密密钥用于 Commissioning 后续通信消息进行加、解密和完…...
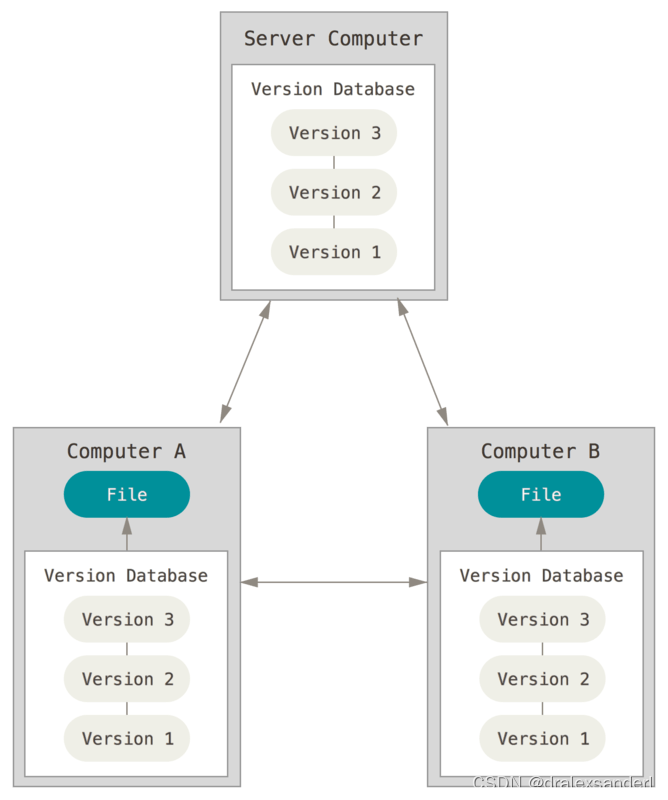
版本控制背景知识
版本控制背景知识 本文是关于 Git 系列文章的导读，我们先介绍一下版本控制的背景知识。 什么是版本控制 版本控制是一种记录一个或若干文件内容变化，以便将来查阅特定版本修订情况的系统。它将什么时候、什么人更改了文件的什么内容等信息如实记录下来…...
tensorflow报错: DNN library is no found
错误描述 如上图在执行程序的时候，会出现 DNN library is no found 的报错 解决办法 这个错误基本上说明你安装的 cudnn有问题，或者没有安装这个工具。 首先检测一下你是否安装了 cudnn 进入CUDA_HOME下，也就是进入你的cuda的驱动的安装目…...
DA14531-高级应用篇-用户如何开启OTA服务
文章目录 1. OTA相关文件2.OTA宏定义列表3.OTA主要函数接口4.OTA具体实施步骤5.总结1. OTA相关文件 1）app_suotar_task.c和app_suotar_task.h 2）app_suotar.c和app_suotar.h 2.OTA宏定义列表 宏定义注解CFG_PRF_SUOTAR用户开启SOTA功能BLE_SUOTA_RECEIVERSOTA功能服务CFG_S…...
国内镜像源配置方法（包括临时和永久方法）
国内镜像源： 阿里云 http://mirrors.aliyun.com/pypi/simple/中国科技大学 https://pypi.mirrors.ustc.edu.cn/simple/豆瓣 http://pypi.douban.com/simplePython官方 https://pypi.python.org/simple/v2ex http://pypi.v2ex.com/simple/中国科学院 http://pypi.mi…...
数据结构二叉树--堆（数据结构实现和堆排序的一种实现）
堆是一个数据结构 逻辑结构：完全二叉树（要求父节点大于孩子节点或者小于孩子节点） 存储结构：顺序存储 typedef int DataType; typedef struct Heap{DataType*data;int size;int capacity; }Heap;void InitHeap(Heap*pH) {asser…...
CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO：支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题：MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者：Yanyuan Chen, Dexuan Xu, Yu Hu…...
突破不可导策略的训练难题：零阶优化与强化学习的深度嵌合
强化学习（Reinforcement Learning, RL）是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程，然后使用强化学习的Actor-Critic机制（中文译作“知行互动”机制），逐步迭代求解…...
AI Agent与Agentic AI：原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例：使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例：使用OpenAI GPT-3进…...
MMaDA: Multimodal Large Diffusion Language Models
CODE ： https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA，它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...
Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库，专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性，并提供了一个通用的框架&…...
JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型（Primitive） 和 对象类型（Object） 两大类，共 8 种（ES11）： 一、原始类型（7种） 1. undefined 定…...
基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发，数据库mysql，前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
医疗AI模型可解释性编程研究：基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践，在这一过程中，模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法（如RandomForest、XGBoost、LightGBM）因其卓越的预测性能和相对良好的解释性…...
小智AI+MCP
什么是小智AI和MCP 如果还不清楚的先看往期文章 手搓小智AI聊天机器人 MCP 深度解析：AI 的USB接口 如何使用小智MCP 1.刷支持mcp的小智固件 2.下载官方MCP的示例代码 Github：https://github.com/78/mcp-calculator 安这个步骤执行 其中MCP_ENDPOI…...
leetcode_69.x的平方根
题目如下 ： 看到题 ，我们最原始的想法就是暴力解决: for(long long i 0;i<INT_MAX;i){if(i*ix){return i;}else if((i*i>x)&&((i-1)*(i-1)<x)){return i-1;}}我们直接开始遍历，我们是整数的平方根，所以我们分两…...