实践学习PaddleScience飞桨科学工具包
实践学习PaddleScience飞桨科学工具包
动手实践,在实践中学习!本项目可以在AIStudio平台一键运行!地址:https://aistudio.baidu.com/projectdetail/4278591 本项目第一次执行会报错,再执行一次即可。若碰到莫名其妙的报错,换成32G显存环境试试。
要平视爱因斯坦和牛顿
爱因斯坦和牛顿也是普通人,也有认识不到的地方,不要盲目崇拜,也不要一味否定前人的实践,而要对前人的成果,尊重客观事实,辩证的一分为二的学习、实践和吸收,要站在牛顿和爱因斯坦的肩膀上,与他们平视。 --张永德(原话记录,有些许异同)
AIStudio和飞桨科学工具包,沟通理论和实践,让我们与顶级科学家站在同一起跑线上!
一、PaddleScience飞桨科学工具包简介
官网github地址:https://github.com/PaddlePaddle/PaddleScience
PaddleScience 使用可重用的软件组件扩展了 PaddlePaddle 框架,用于开发新颖的科学计算应用程序。此类新应用包括基于物理的机器学习、基于神经网络的 PDE 求解器、CFD 机器学习等。PaddleScience 目前正在积极开发中。它的设计不断发展,其 API 可能会发生变化。
1、核心组件
核心功能和组织
PaddleScience 目前专注于 PINNs 模型。核心组件如下。
Geometry几何学,一个用于定义几何域的声明式接口。支持自动离散化
Neural net神经网络,目前支持可自定义大小和深度的全连接层。
PDE偏微分方程,以符号形式描绘偏微分方程。特定 PDE 派生基本 PDE 类。当前包括两个原生 PDE:Laplace2d 和 NavierStokes2d。
Loss损失,定义在训练过程中执行的确切惩罚。默认情况下,应用 L2 损失。在目前的设计中,总损失是方程损失、边界条件损失和初始条件损失三部分的加权和。
Optimizer优化器,指定用于训练的优化器。Adam 是默认选项。未来将提供更多优化器,例如 BFGS。
Solver求解器,以批处理方式管理给定训练数据的训练过程。
Visualization可视化,可轻松访问图形绘制实用程序。
2、物理信息神经网络(PINN)简介
https://blog.csdn.net/jerry_liufeng/article/details/120727393
【PINN】基于物理信息的神经网络 (Physics Informed Neural Network,简称PINN) 是一种科学机器在传统数值领域的应用方法,特别是用于解决与偏微分方程 (PDE) 相关的各种问题,包括方程求解、参数反演、模型发现、控制与优化等。
大多数物理规律都可以表述为偏微分方程(PDE)的形式。偏微分方程,尤其是高阶偏微分方程难以求解析解,通常是采用各种方式逼近从而获得近似解。而神经网络的强大之处就在于其是万能近似器(universal approximator)
PaddlePaddle的神经网络核心是自动微分,其实一个AI框架主要就是完成两部分:1、Tensor张量的存储与计算 2、自动微分。
飞桨的自动微分是通过trace的方式,记录前向OP的执行,并自动创建反向var和添加相应的反向OP,然后来实现反向梯度计算的。

3、Vtk介绍
参见:https://www.cnblogs.com/zhhfan/p/10312170.html
Vtk,(visualization toolkit)是一个开源的免费软件系统,主要用于三维计算机图形学、图像处理和可视化。Vtk是在面向对象原理的基础上设计和实现的,它的内核是用C++构建的,包含有大约250,000行代码,2000多个类,还包含有几个转换界面,因此也可以自由的通过Java,Tcl/Tk和Python各种语言使用vtk。以下介绍VTK对于STL图像的基本操作
基础概念
- 数据源 resource: cone = vtk.vtkConeSource()
- 映射器 mapper:coneMapper = vtk.vtkPolyDataMapper()
- 映射器添加数据源: coneMapper.SetInput( cone.GetOutput() )
- 演员 actor: coneActor = vtk.vtkActor()
- 演员添加映射器:coneActor.SetMapper( coneMapper )
- 绘制器 renderer: vtk.vtkRenderer()
- 绘制器添加演员:renderer.AddActor( coneActor )
- 绘制窗口 win:vtk.vtkRenderWindow()
- 绘制窗口添加绘制器:renWin.AddRenderer( renderer )
- 窗口读取绘制器生成的图形: renWin.Render()
如何打开vtp文件,见“相关问题和技巧”部分。
二、飞桨科学工具包安装
若只需要执行例子里的.py文件,则只要加上环境变量即可%env PYTHONPATH=/home/aistudio/PaddleScience。见实践三部分。
若需要使用Notebook模式,进行代码分块编写和执行,则需要安装飞桨科学包,本项目里采用手写setup.py安装文件的方式,帮着飞桨科学工具包实现安装功能。见实践一和实践二部分。
1、 环境设置
本项目第一个例子以notebook模式展示,因此需要安装飞桨科学包,步骤会略显繁琐。
安装相关库文件
# 大约需要20秒
!pip install numpy scipy sympy matplotlib vtk pyevtk pandas wget visualdl
下载飞桨科学工具包源码。
源码中有例子可以用来研究学习。
%cd ~/
# !pip install pip -U --user
!git clone https://github.com/PaddlePaddle/PaddleScience # 下载代码# 更新软件,可不执行
# !cd ~/PaddleScience/ && git pull
写安装配置文件
因为原配置文件中包含的库较多,在setup安装时会卡住,所以单独写一个只有一个包的配置文件。
命令行运行这步可省略。
%%writefile ~/PaddleScience/requirements_setup.txt
numpy
写飞桨科学包setup.py安装文件
setup安装之后,就可以不局限于执行路径了。
命令行运行这步可省略。
%%writefile ~/PaddleScience/setup.py
import setuptools
import subprocess
import ostry:version = (subprocess.check_output(["git", "describe", "--abbrev=0", "--tags"]).strip().decode("utf-8"))
except Exception as e:print("Could not get version tag. Defaulting to version 0")version = "0"with open("requirements_setup.txt") as f:requirements = f.read().splitlines()if __name__ == "__main__":with open("README.md", "r") as fh:long_description = fh.read()setuptools.setup(name="paddlescience",version=version,author="PaddlePaddle",author_email="xxxx@baidu.com",description="paddlescience",long_description=long_description,long_description_content_type="text/markdown",url=" ",classifiers=["Programming Language :: Python :: 3","Operating System :: POSIX :: Linux","License :: OSI Approved :: MIT License",],packages=setuptools.find_packages(include=["paddlescience*"], exclude=[]),# package_data={"torchmd": ["config.ini", "logging.ini"],},install_requires=requirements,)2、使用setup安装PaddleScience
使用命令python setup.py install , 其中的setup.py文件就是我们前面写的那个文件。
也可以使用开发模式命令是python setup.py develop
命令行运行这步可省略。
!cd /home/aistudio/PaddleScience/ && python setup.py install
验证
测试一下,看飞桨科学工具包是否安装成功。第一次执行可能报错,重启环境(使setup生效)再次运行即可。
没有error报错则证明安装成功!
命令行运行这步可省略。
# 第一次执行可能报错,重启环境(使setup生效)再次运行即可。
import paddlescience
三、实践1、顶盖驱动型腔流
本指南介绍了如何构建 PINN 模型来模拟 PaddleScience 中的 2d Lid Driven Cavity (LDC) 流动。
1、介绍
LDC 问题模拟了一个充满液体的容器,其中盖子以恒定速度沿水平方向移动。目标是计算系统处于稳态时容器中每个内部点的液体速度。
下图显示了训练 100 x 100 网格生成的结果。分别显示速度的垂直和水平分量。

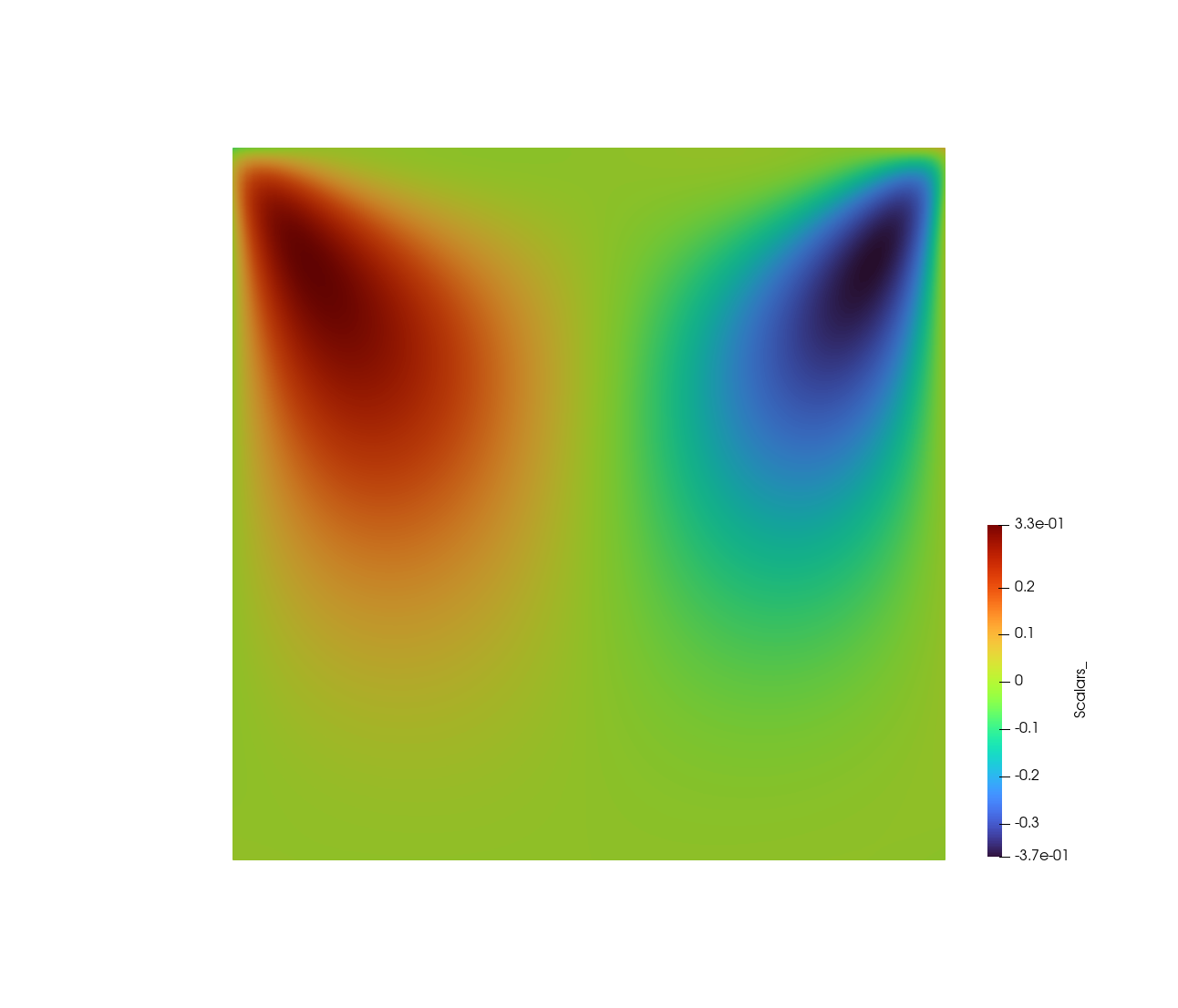
2、如何构建PINN模型
PINN 模型由过去的传统 PDE 设置和近似解的神经网络共同组成。PDE 部分包括执行物理定律的特定微分方程、限定问题域的几何形状以及可以找到解决方案的初始和边界值条件。神经网络部分可以采用深度学习工具包中广泛存在的典型前馈网络的变体。
要获得 PINN 模型,需要训练神经网络。正是在这个阶段,PDE 的信息通过反向传播被灌输到神经网络中。损失函数在控制如何分配这些信息方面起着至关重要的作用,强调 PDE 的不同方面,例如,通过调整方程残差和边界值的权重。
概念明确后,接下来让我们看一下如何将其转换为 ldc2d 示例。
3、构造几何体psci.geometry
首先,使用模块接口定义问题几何体。在此示例中,几何体是一个矩形,其原点位于坐标 (-0.05, -0.05),范围设置为 (0.05, 0.05)。
# %cd ~/PaddleScience/
import paddlescience as psci
import numpy as npgeo = psci.geometry.Rectangular(origin=(-0.05, -0.05), extent=(0.05, 0.05))
接下来,为几何图形添加边界,这些边界将在 PDE 中使用。请注意,该geo.add_boundary函数仅用于具有物理约束的边界。
geo.add_boundary(name="top", criteria=lambda x, y: abs(y - 0.05) < 1e-5)
geo.add_boundary(name="down", criteria=lambda x, y: abs(y + 0.05) < 1e-5)
geo.add_boundary(name="left", criteria=lambda x, y: abs(x + 0.05) < 1e-5)
geo.add_boundary(name="right", criteria=lambda x, y: abs(x - 0.05) < 1e-5)准备好域后,给出离散化方法。
npoints = 10201
geo_disc = geo.discretize(npoints=npoints, method="uniform")4、构建偏微分方程
定义几何部分后,定义要求解的 PDE 方程。在本例中,方程是 2d Navier Stokes。这个方程存在于科学工具包中,只需要创建一个psci.pde.NavierStokes对象来设置方程。
pde = psci.pde.NavierStokes(nu=0.01, rho=1.0, dim=2, time_dependent=False, weight=0.0001)接下来,为 PDE 添加边界方程。PDE 中的边界方程与几何中的边界定义密切相关。使用pde.add_bc设置边界上的物理信息.
weight_top_u = lambda x, y: 1.0 - 20.0 * abs(x)
bc_top_u = psci.bc.Dirichlet('u', rhs=1.0, weight=weight_top_u)
bc_top_v = psci.bc.Dirichlet('v', rhs=0.0)
bc_down_u = psci.bc.Dirichlet('u', rhs=0.0)
bc_down_v = psci.bc.Dirichlet('v', rhs=0.0)
bc_left_u = psci.bc.Dirichlet('u', rhs=0.0)
bc_left_v = psci.bc.Dirichlet('v', rhs=0.0)
bc_right_u = psci.bc.Dirichlet('u', rhs=0.0)
bc_right_v = psci.bc.Dirichlet('v', rhs=0.0)pde.add_bc("top", bc_top_u, bc_top_v)
pde.add_bc("down", bc_down_u, bc_down_v)
pde.add_bc("left", bc_left_u, bc_left_v)
pde.add_bc("right", bc_right_u, bc_right_v)一旦准备好方程和问题域,就应该给出离散化方法。此方法将用于在训练开始之前生成训练数据。目前,可以将二维空间离散化为 N×M 网格,在本例中具体为 101×101。
pde_disc = pde.discretize(geo_disc=geo_disc)5、构建神经网络
现在 PDE 部分几乎完成了,我们继续构建神经网络。通过创建psci.network.FCNet对象来定义完全连接的网络很简单。以下是我们如何创建一个由 10 个隐藏层组成的 FFN,每个隐藏层有 20 个神经元,使用双曲正切作为激活函数。
net = psci.network.FCNet(num_ins=2,num_outs=3,num_layers=10,hidden_size=20,activation='tanh')接下来,最重要的步骤之一是定义损失函数。这里我们使用 L2 损失。
loss = psci.loss.L2(p=2)通过设计,该loss对象传达了 PDE 的完整信息。现在结合神经网络和损失,我们创建psci.algorithm.PINNs模型算法。
algo = psci.algorithm.PINNs(net=net, loss=loss)接下来,通过插入 Adam 优化器,构建求解器,就可以开始训练了。在此示例中,使用了 Adam 优化器,并给出了 0.001 的学习率。
该类将此处psci.solver.Solver调用的 PINNs 模型和优化器捆绑到公开接口 algo的求解器对象中。接受一个关键字参数,指定每个批次的 epoch 数。
# 300epoch 用时40秒。30000估计用时4000秒,约一小时7分钟
opt = psci.optimizer.Adam(learning_rate=0.001, parameters=net.parameters())
solver = psci.solver.Solver(pde=pde_disc, algo=algo, opt=opt)
solution = solver.solve(num_epoch=3000) # 30000最后,solver.solve返回一个函数,该函数计算几何中给定点的解值。将该函数应用于几何,将输出转换为 Numpy,然后您可以验证结果。
psci.visu.save_vtk是一个快速可视化的辅助工具。它将图形保存在 vtp 文件中,可以使用Paraview播放。
psci.visu.save_vtk(geo_disc=pde_disc.geometry, data=solution)
# psci.visu.save_vtk(
# time_array=pde_disc.time_array, geo_disc=pde_disc.geometry, data=solution)
##6、 这样顶盖驱动型腔流训练就完成了
期间碰到过从第435个开始None的问题,新飞桨版本已解决该问题。
epoch/num_epoch: 434 / 30000 batch/num_batch: 1 / 1 loss: 66.1305 eq_loss: 66.13051 bc_loss: 8.132067
epoch/num_epoch: 435 / 30000 batch/num_batch: 1 / 1 loss: nan eq_loss: nan bc_loss: nan四、实践2、多孔介质中的达西流
# %cd ~/PaddleScience
import paddlescience as psci
import numpy as np
import paddle
1、构造几何psci.geometry
首先,使用模块接口定义问题几何。在此示例中,几何图形是一个矩形,其原点位于坐标 (0.0, 0.0),范围设置为 (1.0, 1.0)。
psci.config.set_dtype("float32")# ref solution
ref_sol = lambda x, y: np.sin(2.0 * np.pi * x) * np.cos(2.0 * np.pi * y)# ref rhs
ref_rhs = lambda x, y: 8.0 * np.pi**2 * np.sin(2.0 * np.pi * x) * np.cos(2.0 * np.pi * y)# set geometry and boundary
geo = psci.geometry.Rectangular(origin=(0.0, 0.0), extent=(1.0, 1.0))
接下来,为几何图形添加边界,这些边界将在 PDE 中使用。请注意,该geo.add_boundary函数仅用于具有物理约束的边界。
geo.add_boundary(name="top", criteria=lambda x, y: y == 1.0)
geo.add_boundary(name="down", criteria=lambda x, y: y == 0.0)
geo.add_boundary(name="left", criteria=lambda x, y: x == 0.0)
geo.add_boundary(name="right", criteria=lambda x, y: x == 1.0)
准备好域后,应给出离散化方法。
geo_disc = geo.discretize(npoints=npoints, method="uniform")
2、构建偏微分方程
定义几何部分后,定义要求解的 PDE 方程。在本例中,方程是 2d Poisson。这个方程存在于包中,只需要创建一个psci.pde.Poisson对象来设置方程。
pde = psci.pde.Poisson(dim=2, rhs=ref_rhs)
接下来,为 PDE 添加边界方程。PDE 中的边界方程与几何中的边界定义密切相关。需要设置边界上的物理信息,然后使用pde.add_bc.
bc_top = psci.bc.Dirichlet('u', rhs=ref_sol)
bc_down = psci.bc.Dirichlet('u', rhs=ref_sol)
bc_left = psci.bc.Dirichlet('u', rhs=ref_sol)
bc_right = psci.bc.Dirichlet('u', rhs=ref_sol)pde.add_bc("top", bc_top)
pde.add_bc("down", bc_down)
pde.add_bc("left", bc_left)
pde.add_bc("right", bc_right)
一旦准备好方程和问题域,就应该给出离散化方法。此配方将用于在训练开始之前生成训练数据。
pde_disc = pde.discretize(geo_disc=geo_disc)
3、构建神经网络
现在 PDE 部分几乎完成了,我们继续构建神经网络。通过创建psci.network.FCNet对象来定义完全连接的网络很简单。以下是我们如何使用双曲正切作为激活函数创建一个由 5 个隐藏层组成的 FFN,每个隐藏层有 20 个神经元。
net = psci.network.FCNet(num_ins=2, num_outs=1, num_layers=5, hidden_size=20, activation='tanh')
接下来,最重要的步骤之一是定义损失函数。这里我们使用 L2 损失。
loss = psci.loss.L2()
通过设计,该loss对象传达了 PDE 的完整信息。现在结合神经网络和损失,我们创建psci.algorithm.PINNs模型算法。
algo = psci.algorithm.PINNs(net=net, loss=loss)
接下来,通过插入 Adam 优化器,构建求解器,您就可以开始训练了。在此示例中,使用了 Adam 优化器,并给出了 0.001 的学习率。
该类将此处psci.solver.Solver调用的 PINNs 模型和优化器捆绑到公开接口 algo的求解器对象中。接受一个关键字参数,num_epoch指定每个批次的 epoch 数。
100epoch用时3秒,10000估计用时300秒。
opt = psci.optimizer.Adam(learning_rate=0.001, parameters=net.parameters())
solver = psci.solver.Solver(pde=pde_disc, algo=algo, opt=opt)
solution = solver.solve(num_epoch=10000) # 10000最后,solver.solve返回一个函数,该函数计算几何中给定点的解值。将该函数应用于几何,将输出转换为 Numpy,然后您可以验证结果。
psci.visu.save_vtk是一个快速可视化的辅助工具。它将图形保存在 vtp 文件中,可以使用Paraview播放。
psci.visu.save_vtk(geo_disc=pde_disc.geometry, data=solution)# MSE
# TODO: solution array to dict: interior, bc
cord = pde_disc.geometry.interior
ref = ref_sol(cord[:, 0], cord[:, 1])
mse2 = np.linalg.norm(solution[0][:, 0] - ref, ord=2)**2n = 1
for cord in pde_disc.geometry.boundary.values():ref = ref_sol(cord[:, 0], cord[:, 1])mse2 += np.linalg.norm(solution[n][:, 0] - ref, ord=2)**2n += 1mse = mse2 / npointsprint("MSE is: ", mse)
五、实践3、拉普拉斯方程
在 PaddleScience 中为简单的拉普拉斯方程构建 PINN 模型。
若只需要训练.py文件,则可以省略上面所有的步骤,只需要完成下面三步即可:
-
安装相关软件包
!pip install numpy scipy sympy matplotlib vtk pyevtk pandas wget visualdl -
设置环境变量
%env PYTHONPATH=/home/aistudio/PaddleScience -
执行训练程序
!cd ~/PaddleScience/examples/laplace && python laplace2d.py
# cpu 运行5分钟 新版本gpu下1分40秒。
# !pip install numpy scipy sympy matplotlib vtk pyevtk pandas wget visualdl
%env PYTHONPATH=/home/aistudio/PaddleScience
!cd ~/PaddleScience/examples/laplace && python laplace2d.py输出信息
epoch: 22 loss: 0.084736794 eq loss: 0.00025607698 bc loss: 0.0052932343 ic loss: 0.0 data loss: 0.0
epoch: 23 loss: 0.084736794 eq loss: 0.00025607698 bc loss: 0.0052932343 ic loss: 0.0 data loss: 0.0
epoch: 24 loss: 0.084736794 eq loss: 0.00025607698 bc loss: 0.0052932343 ic loss: 0.0 data loss: 0.0
epoch: 25 loss: 0.084736794 eq loss: 0.00025607698 bc loss: 0.0052932343 ic loss: 0.0 data loss: 0.0
MSE is: 4.461478115287425e-06六、实践4、3D绕柱
# 3d 绕柱 15分钟1300epoch。 2000个epoch预计23分钟 。
!cd ~/PaddleScience/examples/cylinder/3d_steady/ && python cylinder3d_steady.py
# 顶盖驱动型腔流 gpu 52分钟
# !cd ~/PaddleScience/examples/ldc && python ldc2d_steady.py
# 多孔介质中的达西流 gpu 6分38秒
# !cd ~/PaddleScience/examples/darcy/ && python darcy2d.py
七、问题和技巧
如何打开vtp文件
可以使用paraview打开vtp文件。
这里也提供了一个readvtp.py文件,放在work目录下。可以将这个文件和vtp文件都下载到本地,然后执行python readvtp.py rslt_u.vtp即可打开该文件,是3d的哦,可以用鼠标旋转看看。 本机需要安装vtk库(pip install vtk)。
新版本科学工具包的存盘文件为vtu,不能用下面的小程序打开(打开后看不到东西)。需要安装下载paraview来打开。
%%writefile ~/work/readvtp.py
import vtkmodules.vtkInteractionStyle
# noinspection PyUnresolvedReferences
import vtkmodules.vtkRenderingOpenGL2
from vtkmodules.vtkCommonColor import vtkNamedColors
from vtkmodules.vtkIOXML import vtkXMLPolyDataReader
from vtkmodules.vtkRenderingCore import (vtkActor,vtkPolyDataMapper,vtkRenderWindow,vtkRenderWindowInteractor,vtkRenderer
)def get_program_parameters():import argparsedescription = 'Read a VTK XML PolyData file.'epilogue = ''''''parser = argparse.ArgumentParser(description=description, epilog=epilogue,formatter_class=argparse.RawDescriptionHelpFormatter)parser.add_argument('filename', help='horse.vtp.')args = parser.parse_args()return args.filenamedef main():colors = vtkNamedColors()filename = get_program_parameters()reader = vtkXMLPolyDataReader()reader.SetFileName(filename)reader.Update()mapper = vtkPolyDataMapper()mapper.SetInputConnection(reader.GetOutputPort())actor = vtkActor()actor.SetMapper(mapper)actor.GetProperty().SetColor(colors.GetColor3d('Tan'))# Create a rendering window and rendererren = vtkRenderer()renWin = vtkRenderWindow()renWin.AddRenderer(ren)renWin.SetWindowName('ReadVTP')# Create a renderwindowinteractoriren = vtkRenderWindowInteractor()iren.SetRenderWindow(renWin)# Assign actor to the rendererren.AddActor(actor)# Enable user interface interactoriren.Initialize()renWin.Render()ren.SetBackground(colors.GetColor3d('AliceBlue'))ren.GetActiveCamera().SetPosition(-0.5, 0.1, 0.0)ren.GetActiveCamera().SetViewUp(0.1, 0.0, 1.0)renWin.Render()iren.Start()if __name__ == '__main__':main()八、调试纠错
报错cannot import name ‘jacobian’
import paddlescienc报错:15 import paddle16 import paddle.nn.functional as F
---> 17 from paddle.autograd import jacobian, hessian, batch_jacobian, batch_hessian18 from ..pde import first_order_rslts, first_order_derivatives, second_order_derivatives19 from .loss_base import LossBase
ImportError: cannot import name 'jacobian' from 'paddle.autograd' (/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/paddle/autograd/__init__.py)估计应该用最新版本才可以!
安装最新develop版本,问题解决!
没有版本ModuleNotFoundError: No module named ‘paddlescience’
要在科学工具包的根目录执行 ,把文件直接放在科学工具包根目录然后执行。
后期是采用setup安装科学工具包的方式来解决路径依赖问题。
OSError: (External) CUBLAS error(7)
OSError: (External) CUBLAS error(7). [Hint: 'CUBLAS_STATUS_INVALID_VALUE'. An unsupported value or parameter was passed to the function (a negative vector size, for example). To correct: ensure that all the parameters being passed have valid values. ] (at /paddle/paddle/fluid/platform/device/gpu/cuda/cuda_helper.h:87)[operator < uniform_random > error]
飞桨版本出错,因为是切换到gpu环境,安装的时候选了cuda11版本的飞桨,安装后报错。
选择飞桨cuda10.1版本的,就ok了
后期是采用系统自带的飞桨2.3正式版本,就没有安装的烦恼了。
执行python ldc2d.py的时候报错
epoch/num_epoch: 29999 / 30000 batch/num_batch: 1 / 1 loss: 0.83008355 eq_loss: 0.5134626 bc_loss: 0.652223
epoch/num_epoch: 30000 / 30000 batch/num_batch: 1 / 1 loss: 0.7781308 eq_loss: 0.47800368 bc_loss: 0.61400324
Traceback (most recent call last):File "ldc2d.py", line 97, in <module>openfoam_u = np.load("./openfoam/openfoam_u_100.npy")File "/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/numpy/lib/npyio.py", line 417, in loadfid = stack.enter_context(open(os_fspath(file), "rb"))
FileNotFoundError: [Errno 2] No such file or directory: './openfoam/openfoam_u_100.npy'
原来是还有一个目录没有cp到当前目录,使用命令cp -r examples/ldc2d/openfoam . 即可。
后期是采用setup安装科学工具包来解决路径依赖问题。
报错unexpected keyword argument ‘space_steps’
---------------------------------------------------------------------------TypeError Traceback (most recent call last)/tmp/ipykernel_444/2834758931.py in <module>
----> 1 pdes, geo = psci.discretize(pdes, geo, space_steps=(101, 101))
TypeError: discretize() got an unexpected keyword argument 'space_steps'
原因是应该是space_nsteps,命令为pdes, geo = psci.discretize(pdes, geo, space_steps=(101, 101)) ,文档有误。
新版本已经解决该问题。
报错Received [3] in X is not equal to [2] in Y at i:1
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/paddle/fluid/dygraph/math_op_patch.py in __impl__(self, other_var)262 axis = -1263 math_op = getattr(_C_ops, op_type)
--> 264 return math_op(self, other_var, 'axis', axis)265 266 comment = OpProtoHolder.instance().get_op_proto(op_type).comment
ValueError: (InvalidArgument) Broadcast dimension mismatch. Operands could not be broadcast together with the shape of X = [400, 3] and the shape of Y = [400, 2]. Received [3] in X is not equal to [2] in Y at i:1.[Hint: Expected x_dims_array[i] == y_dims_array[i] || x_dims_array[i] <= 1 || y_dims_array[i] <= 1 == true, but received x_dims_array[i] == y_dims_array[i] || x_dims_array[i] <= 1 || y_dims_array[i] <= 1:0 != true:1.] (at /paddle/paddle/pten/kernels/hybird/general/elementwise_base.h:373)[operator < elementwise_sub > error]
解决方法,将pdes.set_bc_value(bc_value=bc_value)修改为:
pdes.set_bc_value(bc_value=bc_value, bc_check_dim=[0, 1])
30000步报None
epoch/num_epoch: 29999 / 30000 batch/num_batch: 1 / 1 loss: nan eq_loss: nan bc_loss: nan
epoch/num_epoch: 30000 / 30000 batch/num_batch: 1 / 1 loss: nan eq_loss: nan bc_loss: nan
MSE_u: nan
MSE_v: nan
MSE_u_400: nan
MSE_v_400: nan
通过报issue得知,换新的飞桨开发版就好了。
最终飞桨2.3正式版之后的都可以。
环境变量设置问题
在AIStudio notebook下环境变量设置有些坑,比如命令行下使用export PYTHONPATH=$PYTHONPATH:/home/aistudio/PaddleScience/,然后就可以正常使用科学包了。而在notebook下,使用%env PYTHONPATH=$PYTHONPATH:/home/aistudio/PaddleScience/或者env PYTHONPATH=/home/aistudio/PaddleScience/都不能正常导入科学工具包,即import paddlescience会报错。
最终解决方法是写setup.py文件,手动安装科学工具包。
报错hijack_call.c:658 cuInit error unknown error
!python laplace2d.py 报错
重启,用飞桨2.3版本
报错No module named ‘sympy’
import sympy
ModuleNotFoundError: No module named 'sympy'
解决方法:使用AIStudio经典版。即不使用BML版本。
结束语
用飞桨,划时代!让我们荡起双桨,在AI的海洋乘风破浪!
飞桨官网:https://www.paddlepaddle.org.cn
因为水平有限,难免有不足之处,还请大家多多帮助。
作者:段春华, 网名skywalk 或 天马行空,济宁市极快软件科技有限公司的AI架构师,百度飞桨PPDE。
我在AI Studio上获得至尊等级,点亮11个徽章,来关注啊~ https://aistudio.baidu.com/aistudio/personalcenter/thirdview/141218
相关文章:

实践学习PaddleScience飞桨科学工具包
实践学习PaddleScience飞桨科学工具包 动手实践,在实践中学习!本项目可以在AIStudio平台一键运行!地址:https://aistudio.baidu.com/projectdetail/4278591 本项目第一次执行会报错,再执行一次即可。若碰到莫名其妙的…...
Vue 中修改 Element 组件的 下拉菜单(Dropdown) 的样式
Vue 中修改 Element 组件的 下拉菜单(Dropdown) 的样式 今天在项目中碰到一个 UI 改造的需求,需要根据设计图把页面升级成 UI 设计师提供的设计图样式。 到最后页面改造完了,但是 UI 提供的下拉菜单样式全部是黑色半透明的,只能硬着头皮改了。…...

达梦数据库主备集群
1:服务器硬件需求 按实际业务需求,选择合适的服务器,准备 3 台服务器,一台主库服务器,一台备库服务器,一台监视器服务器,服务器参数建议如下: 硬件要求物理内存>16 GB交换区Swa…...

Spark Doris Connector 可以支持通过 Spark 读取 Doris 数据类型不兼容报错解决
1、版本介绍: doris版本: 1.2.8Spark Connector for Apache Doris 版本: spark-doris-connector-3.3_2.12-1.3.0.jar:1.3.0-SNAPSHOTspark版本:spark-3.3.1 2、Spark Doris Connector Spark Doris Connector - Apache Doris 目…...

深入理解 go chan
go 里面,在实际程序运行的过程中,往往会有很多协程在执行,通过启动多个协程的方式,我们可以更高效地利用系统资源。 而不同协程之间往往需要进行通信,不同于以往多线程程序的那种通信方式,在 go 里面是通过…...
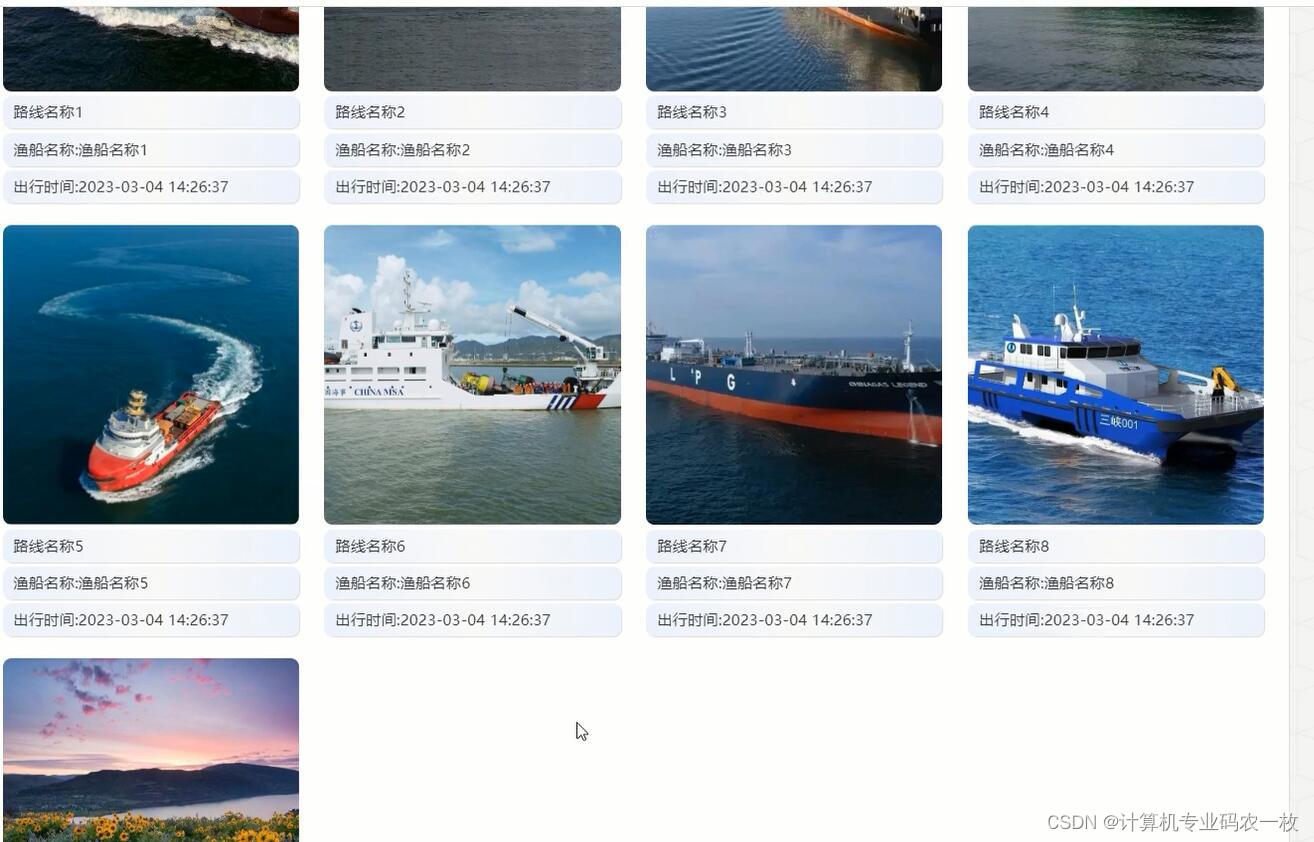
java+vue基于Spring Boot的渔船出海及海货统计系统
该渔船出海及海货统计系统采用B/S架构、前后端分离进行设计,并采用java语言以及springboot框架进行开发。该系统主要设计并完成了管理过程中的用户注册登录、个人信息修改、用户信息、渔船信息、渔船航班、海货价格、渔船海货、非法举报、渔船黑名单等功能。该系统操…...
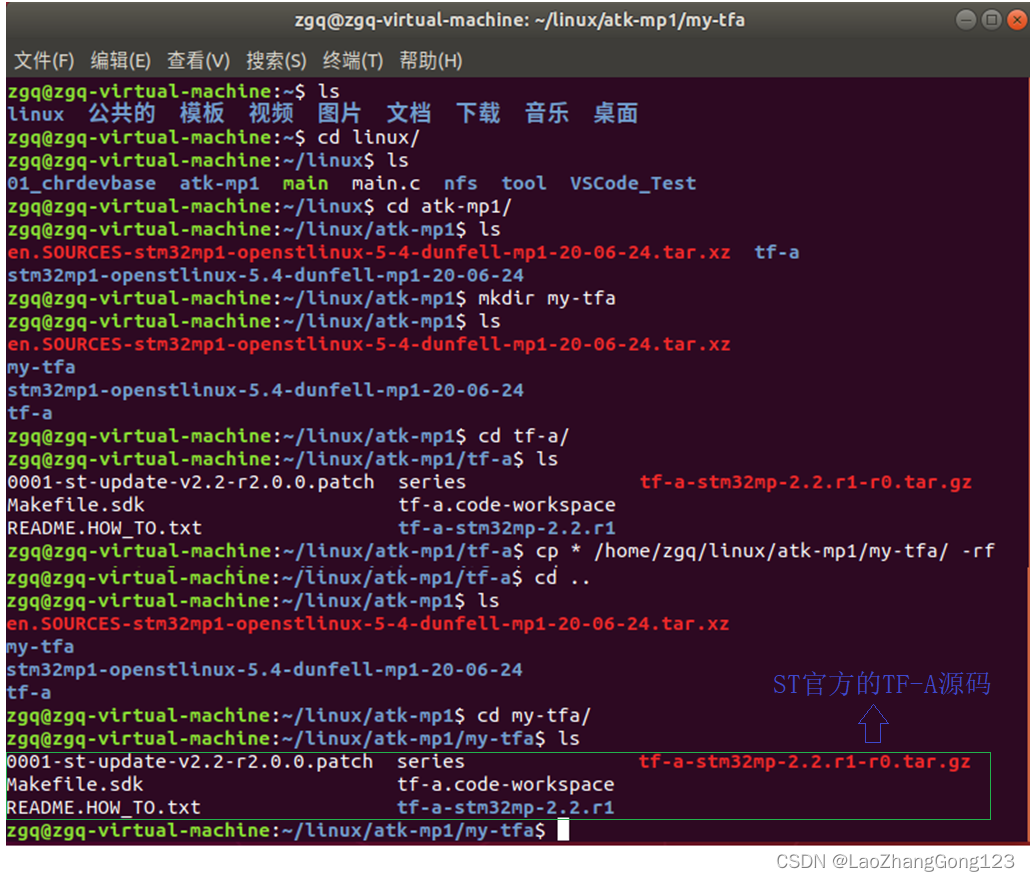
Linux第25步_在虚拟机中备份“ST官方的TF-A源码”
TF-A是ARM公司提供的,ST公司通过修改它,做了一个自己的TF-A代码。因为在后期开发中,若硬件被改变了,我们需要通过修改"ST官方的TF-A源码"就可以自己的TF-A代码了。为了防止源文件被误改了,我们需要将"S…...
统计学-R语言-4.1
文章目录 前言编写R函数图形的控制和布局par函数layout函数 练习 前言 安装完R软件之后就可以对其进行代码的编写了。 编写R函数 如果对数据分析有些特殊需要,已有的R包或函数不能满足,可以在R中编写自己的函数。函数的定义格式如下所示: …...

C++(1) —— 基础语法入门
目录 一、C初识 1.1 第一个C程序 1.2 注释 1.3 变量 1.4 常量 1.5 关键字 1.6 标识符命名规则 二、数据类型 2.1 整型 2.2 sizeof 关键字 2.3 实型(浮点型) 2.4 字符型 2.5 转义字符 2.6 字符串型 2.7 布尔类型 bool 2.8 数据的输入 三…...
构建基于RHEL8系列(CentOS8,AlmaLinux8,RockyLinux8等)的支持63个常见模块的PHP8.1.20的RPM包
本文适用:rhel8系列,或同类系统(CentOS8,AlmaLinux8,RockyLinux8等) 文档形成时期:2023年 因系统版本不同,构建部署应略有差异,但本文未做细分,对稍有经验者应不存在明显障碍。 因软件世界之复杂和个人能力…...
)
Vue-插槽(Slots)
1. 介绍 在Vue.js中,插槽是一种强大的功能,它允许你创建可重用的模板,并在使用该模板的多个地方插入自定义内容。 插槽为你提供了一种方式,可以在父组件中定义一些“插槽”,然后在子组件中使用这些插槽,插…...

新火种AI|GPT-5前瞻!GPT-5将具备哪些新能力?
作者:小岩 编辑:彩云 Sam Altman在整个AI领域,乃至整个科技领域都被看作是极具影响力的存在,而2023年OpenAI无限反转的宫斗事件更是让Sam Altman刷足了存在感,他甚至被《时代》杂志评为“2023年度CEO”。 也正因此&…...
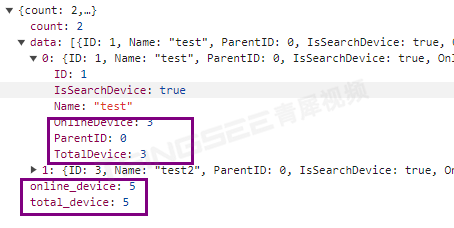
安防视频监控系统EasyCVR设备分组中在线/离线数量统计的开发与实现
安防视频监控EasyCVR系统具备较强的兼容性,它可以支持国标GB28181、RTSP/Onvif、RTMP,以及厂家的私有协议与SDK,如:海康ehome、海康sdk、大华sdk、宇视sdk、华为sdk、萤石云sdk、乐橙sdk等。EasyCVR平台可覆盖多类型的设备接入&am…...

spring cloud之集成sentinel
写在前面 源码 。 本文一起看下spring cloud的sentinel组件的使用。 1:准备 1.1:理论 对于一个系统来说,最重要的就是高可用,那么如何实现高可用呢?你可能会说,集群部署不就可以了,但事实并…...

让车辆做到“耳听八方”,毫米波雷达芯片与系统设计
摘要: 毫米波雷达,是指工作在毫米波波段(一般为30~300GHz频域,波长1~10mm)探测的雷达。毫米波雷达体积小、质量轻、空间分辨率高,穿透“雾烟灰”的能力强,还具备全天候全天时工作的优势。在智能网联汽车体系中,毫米波雷达是系统感知层不可或缺的重要硬件,能让智能驾…...

Python如何实现数据驱动的接口自动化测试
大家在接口测试的过程中,很多时候会用到对CSV的读取操作,本文主要说明Python3对CSV的写入和读取。下面话不多说了,来一起看看详细的介绍吧。 1、需求 某API,GET方法,token,mobile,email三个参数 token为必填项mobil…...

高级分布式系统-第15讲 分布式机器学习--联邦学习
高级分布式系统汇总:高级分布式系统目录汇总-CSDN博客 联邦学习 两种常见的架构:客户-服务器架构和对等网络架构 联邦学习在传统的分布式机器学习基础上的变化。 传统的分布式机器学习:在数据中心或计算集群中使用并行训练,因为…...

小程序基础学习(事件处理)
原理:组件内部设置点击事件,然后冒泡到页面捕获点击事件 在组件内部设置点击事件 处理点击事件,并告诉页面 页面捕获点击事件 页面处理点击事件 组件代码 <!--components/my-info/my-info.wxml--> <view class"title"…...
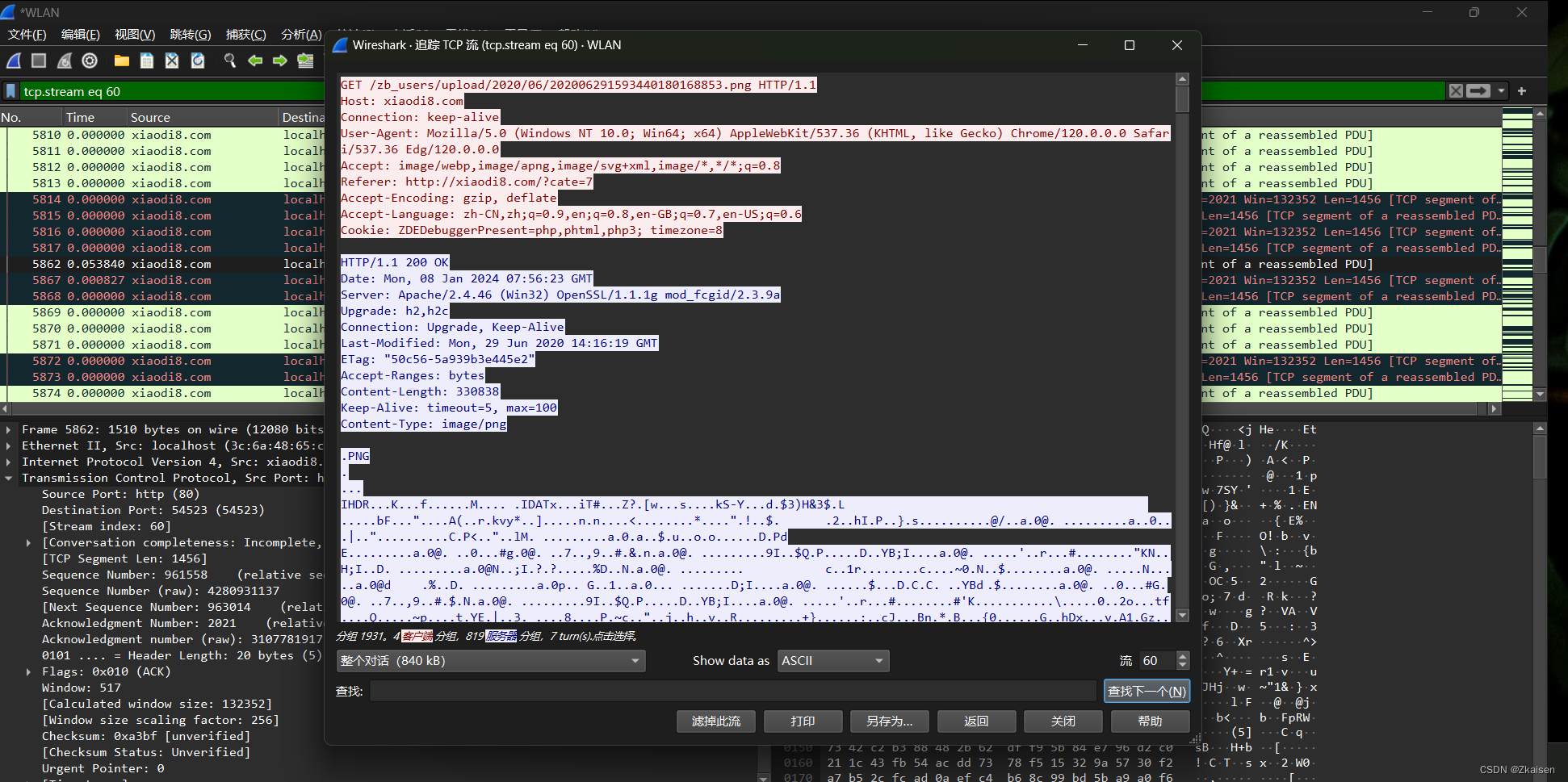
网络协议与攻击模拟_01winshark工具简介
一、TCP/IP协议簇 网络接口层(没有特定的协议) 物理层:PPPOE宽带拨号(应用场景:宽带拨号,运营商切网过来没有固定IP就需要拨号,家庭带宽一般都采用的是拨号方式)数据链路层网络层…...

【linux学习笔记】网络
目录 【linux学习笔记】网络检查、监测网络ping-向网络主机发送特殊数据包traceroute-跟踪网络数据包的传输路径netstat-检查网络设置及相关统计数据 通过网络传输文件ftp 【linux学习笔记】网络 检查、监测网络 ping-向网络主机发送特殊数据包 最基本的网络连接命令就是pin…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...
