数学建模--PageRank算法的Python实现
文章目录
- 1. P a g e R a n k PageRank PageRank算法背景
- 2. P a g e R a n k PageRank PageRank算法基础
- 2.1. P a g e R a n k PageRank PageRank问题描述
- 2.2.有向图模型
- 2.3.随机游走模型
- 3. P a g e R a n k PageRank PageRank算法定义
- 4. P a g e R a n k PageRank PageRank算法计算
- 4.1.幂迭代法
- 4.2.特征值法
- 4.3.代数法
- 5. P a g e R a n k PageRank PageRank算法计算实例
- 6.算法工作源代码
- 7.参考资料
1. P a g e R a n k PageRank PageRank算法背景
P a g e R a n k PageRank PageRank 算法是现代数据科学中用于图链接分析的经典方法,最初由 L a r r y Larry Larry P a g e Page Page 和 S e r g e y Sergey Sergey B r i n Brin Brin 在1996年提出。两位斯坦福大学研究生认为互联网上的链接结构能够反映页面的重要性,与当时基于关键词的搜索方法形成对比。这一独特观点不仅赢得了学术界的认可,也为后来创建的 G o o g l e Google Google搜索引擎奠定了基础。
P a g e R a n k PageRank PageRank的核心思想基于有向图上的随机游走模型,即一阶马尔可夫链。描述了随机游走者如何沿着图的边随机移动,最终收敛到一个平稳分布。在这分布中,每个节点被访问的概率即为其 P a g e R a n k PageRank PageRank 值,代表节点的重要性。 P a g e R a n k PageRank PageRank是递归定义的,计算需要迭代方法,因为一个页面的值部分取决于链接到它的其他页面的值。尽管最初设计用于互联网页面,但 P a g e R a n k PageRank PageRank 已广泛应用于社会影响力、文本摘要等多个领域,展示了其在图数据上的强大实用性。
2. P a g e R a n k PageRank PageRank算法基础
2.1. P a g e R a n k PageRank PageRank问题描述
P a g e R a n k PageRank PageRank 算法是互联网早期用于评估网页重要性的方法。其核心概念是将互联网视为一个有向图,其中每个网页是一个节点,超链接是有向边。通过建立一阶马尔可夫链的随机游走模型,模拟虚拟网页浏览者随机跳转,最终形成一个平稳分布。每个网页的 P a g e R a n k PageRank PageRank 值代表其在这个分布中的概率,即重要性。
举例说明,如下图所示,假设有三个网页 A A A、 B B B 和 C C C, A A A 链接到 B B B 和 C C C, B B B 只链接到 C C C,而 C C C 只链接到 A A A。随机游走模型中,从 A A A 出发的浏览者有 50% 的概率跳转到 B B B 或 C C C;从 B B B 出发的浏览者会 100% 跳转到 C C C;从 C C C 出发的浏览者会 100% 跳转到 A A A。经过多次迭代, C C C 的 P a g e R a n k PageRank PageRank 值可能比 A A A 和 B B B 高,因为它接收到了 A A A 和 B B B 的流量。

P a g e R a n k PageRank PageRank算法直观上认为,一个网页被指向的超链接越多,随机跳转到该网页的概率越高,其 P a g e R a n k PageRank PageRank值越高,表示网页越重要。反之,指向该网页的 P a g e R a n k PageRank PageRank值越高,该网页 P a g e R a n k PageRank PageRank值也越高,表明其重要性增加。PageRank值依赖于网络拓扑结构,一旦确定, P a g e R a n k PageRank PageRank值也确定。计算通过迭代,在互联网有向图上进行。初始假设一个分布,通过迭代计算所有网页的 P a g e R a n k PageRank PageRank值直至收敛。有向图和随机游走模型定义了 P a g e R a n k PageRank PageRank的基本原理,而基本定义对应于理想情况,一般定义则考虑实际网络中的复杂性。
2.2.有向图模型
有向图( D i r e c t e d Directed Directed G r a p h Graph Graph)是图论的基本概念,由节点和有向边组成。每条边有起始节点和终止节点,表示方向性。在互联网中,每个网页可看作有向图中的一个节点,超链接则表示有向边。
以三个网页 A、B 和 C 为例,网页 A 包含指向 B 和 C 的链接,B 包含指向 C 的链接,而 C 包含指向 A 的链接。这构成有向图的边集合,即 E={(A,B),(A,C),(B,C),(C,A)}。
有向图中的周期性结构可通过路径的长度判断,例如,从节点 A 出发返回 A 需要经过长度为 3 的倍数的路径。这样的有向图被称为周期性图。

2.3.随机游走模型
给定一个含有 n n n个结点的有向图,在有向图上定义随机游走( R a n d o m Random Random W a l k Walk Walk)模型,即一阶马尔可夫链,其中结点表示状态,有向边表示状态之间的转移,假设从一个结点到通过有向边相连的所有结点的转移概率相等。具体地,转移矩阵是一个 n n n阶矩阵。
M = [ m i j ] n × n M=[m_{ij}]_{n\times n} M=[mij]n×n
第 i i i行第 j j j列的元素 m i j m_{ij} mij取值规则如下:如果结点 j j j有有 k k k个有向边连出,并且结点 i i i是其连出的一个结点则 m i j = 1 k m_{ij}=\frac{1}{k} mij=k1,否则 m i j = 0 m_{ij}=0 mij=0.
注意转移矩阵 M M M具有如下约束条件:
m i j ≥ 0 m_{ij}\geq0 mij≥0
∑ i = 1 n m i j = 1 \sum_{i=1}^nm_{ij}=1 i=1∑nmij=1
即每个元素非负,每列元素之和为1即矩阵 M M M为随机矩阵( s t o c h a s t i c stochastic stochastic m a t r i x matrix matrix)。
在有向图上的随机游走形成马尔可夫链。也就是说,随机游走者每经过一个单位时间转移一个状态。如果当前时刻在第 i i i 个结点(状态),那么下一个时刻在第 j j j 个结点(状态)的概率是 P i j P_{ij} Pij。这一概率只依赖于当前的状态,与过去无关,具有马尔可夫性。
3. P a g e R a n k PageRank PageRank算法定义
3.1. P a g e R a n k PageRank PageRank算法基本定义
给定一个包含 n n n 个结点的强连通且非周期性的有向图,在其基础上定义随机游走模型。假设转移矩阵为 M M M,在时刻 0 , 1 , 2 , … , t , … 0, 1, 2, \dots, t, \dots 0,1,2,…,t,…,访问各个结点的概率分布为 p 0 , p 1 , p 2 , … , p t , … \mathbf{p}_0, \mathbf{p}_1, \mathbf{p}_2, \dots, \mathbf{p}_t, \dots p0,p1,p2,…,pt,…。其中, v 0 \mathbf{v}_0 v0 是初始概率分布。
p 0 = v 0 , p t + 1 = p t ⋅ M \mathbf{p}_0 = \mathbf{v}_0, \quad \mathbf{p}_{t+1} = \mathbf{p}_t \cdot M p0=v0,pt+1=pt⋅M
则极限为:
lim t → ∞ M t R 0 = R \lim_{t\to\infty}M^tR_0=R t→∞limMtR0=R
存在极限向量 R R R表示马尔可夫链的平稳分布,满足:
M R = R MR=R MR=R
平稳分布 R R R称为这个有向图的 P a g e R a n k PageRank PageRank。 R R R的各个分量称为各个结点的 P a g e R a n k PageRank PageRank值。
R = [ P R ( v 1 ) P R ( v 2 ) ⋮ P R ( v n ) ] \left.R=\left[\begin{array}{c}PR\left(v_1\right)\\PR\left(v_2\right)\\\vdots\\PR\left(v_n\right)\end{array}\right.\right] R= PR(v1)PR(v2)⋮PR(vn)
其中
P R ( v i ) = ∑ v j ∈ M ( v i ) P R ( v j ) L ( v j ) , i = 1 , 2 , ⋯ , n PR\left(v_i\right)=\sum_{v_j\in M\left(v_i\right)}\frac{PR\left(v_j\right)}{L\left(v_j\right)},\quad i=1,2,\cdots,n PR(vi)=vj∈M(vi)∑L(vj)PR(vj),i=1,2,⋯,n
这里 M ( v i ) M(v_i) M(vi) 表示指向结点 v i v_i vi的结点集合, L ( v j ) L(v_j) L(vj) 表示结点 v j v_j vj 连出的有向边的个数。
3.2. P a g e R a n k PageRank PageRank算法一般定义
为了考虑到用户不仅会通过点击链接来浏览网页,还可能随机选择一个网页。因此需要在基本定义的基础上导入平滑项阻尼因子。阻尼因子 d d d 取值由经验决定,例如 d = 0.85 d=0.85 d=0.85。当 d d d 接近1时,随机游走主要依照转移矩阵 M M M 进行;当 d d d 接近0时,随机游走主要以等概率随机访问各个结点。
R = ( d M + 1 − d n E ) R = d M R + 1 − d n 1 \begin{aligned}R&=(dM+\frac{1-d}n\mathbf{E})R\\&=dMR+\frac{1-d}n1\end{aligned} R=(dM+n1−dE)R=dMR+n1−d1
相当于:
P R ( v i ) = d ( ∑ v j ∈ M ( v i ) P R ( v j ) L ( v j ) ) + 1 − d n , i = 1 , 2 , ⋯ , n PR\left(v_i\right)=d\left(\sum_{v_j\in M\left(v_i\right)}\frac{PR\left(v_j\right)}{L\left(v_j\right)}\right)+\frac{1-d}n,\quad i=1,2,\cdots,n PR(vi)=d vj∈M(vi)∑L(vj)PR(vj) +n1−d,i=1,2,⋯,n
4. P a g e R a n k PageRank PageRank算法计算
4.1.幂迭代法
首先给每个页面赋予随机的PR值,然后通过 P n + 1 = A ⋅ P n P_{n+1} = A \cdot P_n Pn+1=A⋅Pn 不断地迭代 P R PR PR值。当满足下面的不等式后迭代结束,获得所有页面的 P R PR PR值:
∣ P n + 1 − P n ∣ < ϵ |P_{n+1}-P_n|<\epsilon ∣Pn+1−Pn∣<ϵ
其中, ϵ \epsilon ϵ是预先定义的小正数。
4.2.特征值法
特征值法是一种用于求解线性代数问题的方法,其中之一就是求解矩阵的特征值和特征向量。在上述描述中,特征值法用于分析 M a r k o v Markov Markov 链的收敛行为。
具体来说,对于一个方阵 A A A,其特征值( e i g e n v a l u e s eigenvalues eigenvalues) λ \lambda λ 和对应的特征向量( e i g e n v e c t o r s eigenvectors eigenvectors) v \mathbf{v} v满足以下方程:
A ⋅ v = λ ⋅ v A \cdot \mathbf{v} = \lambda \cdot \mathbf{v} A⋅v=λ⋅v
这个方程可以重写为 ( A − λ ⋅ I ) ⋅ v = 0 (A - \lambda \cdot I) \cdot \mathbf{v} = \mathbf{0} (A−λ⋅I)⋅v=0,其中 I I I 是单位矩阵。
对于 M a r k o v Markov Markov 链的情况,我们考虑转移矩阵 A A A。特征值法告诉我们,当 A A A 的特征值中存在一个值为 1 时,对应的特征向量可以用来表示 Markov 链的收敛状态。这个特征向量的所有分量均为正,而且是唯一的。
在 P a g e R a n k PageRank PageRank 算法中,我们通过不断迭代
P n + 1 = A ⋅ P n P_{n+1} = A \cdot P_n Pn+1=A⋅Pn
来逼近这个特征向量,直到收敛。这就是特征值法在 P a g e R a n k PageRank PageRank 算法中的应用。
4.3.代数法
相似的,当上面提到的 M a r k o v Markov Markov链收敛时,必有:
P = A P ⇒ P = ( α S + ( 1 − α ) N e e T ) P 方量都为 1 的列向量, P 的所有分量之和为 1 ⇒ P = α S P + ( 1 − α ) N e ⇒ ( e e T − α S ) P = ( 1 − α ) N e ⇒ P = ( e e T − α S ) − 1 ( 1 − α ) N e \begin{gathered} P=AP \\ \Rightarrow P=(\alpha S+\frac{(1-\alpha)}Nee^T)P \\ \text{方量都为}1\text{的列向量,}P\text{的所有分量之和为}1 \\ \Rightarrow P=\alpha SP+\frac{(1-\alpha)}Ne \\ \Rightarrow(ee^T-\alpha S)P=\frac{(1-\alpha)}Ne \\ \Rightarrow P=(ee^T-\alpha S)^{-1}\frac{(1-\alpha)}Ne \end{gathered} P=AP⇒P=(αS+N(1−α)eeT)P方量都为1的列向量,P的所有分量之和为1⇒P=αSP+N(1−α)e⇒(eeT−αS)P=N(1−α)e⇒P=(eeT−αS)−1N(1−α)e
5. P a g e R a n k PageRank PageRank算法计算实例
利用 P a g e R a n k PageRank PageRank算法计算下图每一个结点对应的 P R PR PR:

迭代过程与最后结果如下所示:
| Iteration | A | B | C | D | E |
|---|---|---|---|---|---|
| 1 | 0.2 | 0.087 | 0.087 | 0.1235 | 0.2455 |
| 2 | 0.2387 | 0.09762 | 0.09762 | 0.1391 | 0.2727 |
| 3 | 0.2618 | 0.1042 | 0.1042 | 0.1485 | 0.289 |
| 4 | 0.2757 | 0.1081 | 0.1081 | 0.154 | 0.2988 |
| 5 | 0.28396 | 0.11045 | 0.11045 | 0.1574 | 0.3046 |
| 6 | 0.28892 | 0.11186 | 0.11186 | 0.1594 | 0.3081 |
| 7 | 0.2919 | 0.1127 | 0.1127 | 0.1606 | 0.3102 |
| 8 | 0.29368 | 0.11321 | 0.11321 | 0.1613 | 0.3115 |
| 9 | 0.29475 | 0.11351 | 0.11351 | 0.1618 | 0.3122 |
| 10 | 0.29539 | 0.11369 | 0.11369 | 0.162 | 0.3127 |
| 11 | 0.29577 | 0.1138 | 0.1138 | 0.1622 | 0.3129 |
| 12 | 0.296 | 0.11387 | 0.11387 | 0.1623 | 0.3131 |
| 13 | … | … | … | … | … |
| 21 | 0.296 | 0.113 | 0.113 | 0.162 | 0.313 |
| Final | 0.296 | 0.113 | 0.113 | 0.162 | 0.313 |
6.算法工作源代码
6.1.绘制图网络代码
#绘制有向图
import networkx as nx
import matplotlib.pyplot as plt
G = nx.DiGraph()
nodes = ["A", "B", "C", "D", "E"]
G.add_nodes_from(nodes)
edges = [("A", "B"), ("A", "C"), ("A", "D"), ("B", "D"), ("C", "E"), ("D", "E"), ("B", "E"), ("E", "A")]
G.add_edges_from(edges)
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_size=700, node_color='skyblue', font_size=10, font_color='black',font_weight='bold', arrowsize=20, connectionstyle='arc3,rad=0.1')
#plt.savefig("Graph.png")#随机的图像
plt.show()
6.2. P a g e R a n k PageRank PageRank算法Python代码实现
from pygraph.classes.digraph import digraph
import networkx as nx
import matplotlib.pyplot as plt
class PRIterator:"""计算一张图中的PR值"""def __init__(self, dg):self.damping_factor = 0.85 # 阻尼系数,即αself.max_iterations = 100 # 最大迭代次数self.min_delta = 0.00001 # 确定迭代是否结束的参数,即ϵself.graph = dgdef page_rank(self):# 先将图中没有出链的节点改为对所有节点都有出链for node in self.graph.nodes():if len(self.graph.neighbors(node)) == 0:for node2 in self.graph.nodes():dg.add_edge((node, node2))nodes = self.graph.nodes()graph_size = len(nodes)if graph_size == 0:return {}page_rank = dict.fromkeys(nodes, 1.0 / graph_size) # 给每个节点赋予初始的PR值damping_value = (1.0 - self.damping_factor) / graph_size # 公式中的(1−α)/N部分flag = Falsefor i in range(self.max_iterations):change = 0for node in nodes:rank = 0for incident_page in self.graph.incidents(node): # 遍历所有“入射”的页面rank += self.damping_factor * (page_rank[incident_page] / len(self.graph.neighbors(incident_page)))rank += damping_valuechange += abs(page_rank[node] - rank) # 绝对值page_rank[node] = rankprint("This is NO.%s iteration" % (i + 1))print(page_rank)if change < self.min_delta:flag = Truebreakif flag:print("finished in %s iterations!" % (i + 1))else:print("finished out of 100 iterations!")return page_rank#%%
if __name__ == '__main__':dg = digraph()dg.add_nodes(["A", "B", "C", "D", "E"])dg.add_edge(("A", "B"))dg.add_edge(("A", "C"))dg.add_edge(("A", "D"))dg.add_edge(("B", "D"))dg.add_edge(("C", "E"))dg.add_edge(("D", "E"))dg.add_edge(("B", "E"))dg.add_edge(("E", "A"))pr = PRIterator(dg)page_ranks = pr.page_rank()print("The final page rank is\n", page_ranks)
7.参考资料
[1].https://zhuanlan.zhihu.com/p/137561088
[2].https://zhuanlan.zhihu.com/p/133233438
[3].https://www.mlpod.com/36.html
[4].https://www.cnblogs.com/rubinorth/p/5799848.html
[5].https://zhuanlan.zhihu.com/p/197877312
[6].https://blog.csdn.net/qq_36159768/article/details/108791236
相关文章:

数学建模--PageRank算法的Python实现
文章目录 1. P a g e R a n k PageRank PageRank算法背景2. P a g e R a n k PageRank PageRank算法基础2.1. P a g e R a n k PageRank PageRank问题描述2.2.有向图模型2.3.随机游走模型 3. P a g e R a n k PageRank PageRank算法定义3.1. P a g e R a n k PageRank PageRank…...

samba服务搭建,并将共享目录映射到windows
系统版本:centos7 1、centos 安装samba yum -y install samba 2、查看安装信息 rpm -qa |grep samba 3、设置开机自启动 systemctl enable smb.service systemctl enable nmb.service 4、设置samba服务器配置文件 sudo vi /etc/samba/smb.conf 注意&#…...
golang 中使用 statik 将静态资源编译进二进制文件中
现在的很多程序都会提供一个 Dashboard 类似的页面用于查看程序状态并进行一些管理的功能,通常都不会很复杂,但是其中用到的图片和网页的一些静态资源,如果需要用户额外存放在一个目录,也不是很方便,如果能打包进程序发…...

北京住总集团携手云轴科技ZStack获行业云平台领航者创新实践奖
为进一步促进行业企业上云、用数、赋智发展,落实国家政策,加速云计算应用从互联网拓展至政务、金融、交通、电信等行业,推动以云计算为核心的数字产业创新,1月18日中国信息通信研究院主办的“企业上云用云专项行动会—行业云平台研…...
【漏洞攻击之文件上传条件竞争】
漏洞攻击之文件上传条件竞争 wzsc_文件上传漏洞现象与分析思路编写攻击脚本和重放措施中国蚁剑拿flag wzsc_文件上传 漏洞现象与分析 只有一个upload前端标签元素,并且上传任意文件都会跳转到upload.php页面,判定是一个apache容器,开始扫描…...

Buttton样式设置background属性失效的问题
最近遇到一个之前没有遇见的问题,就是在添加Button控件的时候发现对其设置background时没有效果,原因是AndroidStudio升级后默认按钮就是主题色,一个比较简单的方法是将Button改为android.widget.Button,对比效果如下:…...
使用vue-pdf插件加载pdf
安装: // 安装这个版本,其它版本会有千奇百怪的错,这个版本和4.0.0都是可以的 cnpm install vue-pdf4.2.0// 安装pdfjs-dist cnpm install pdfjs-dist2.5.207 使用: // 我的css样式是pxToRem,友友们使用可能样式会有…...
BP蓝图映射到C++笔记1
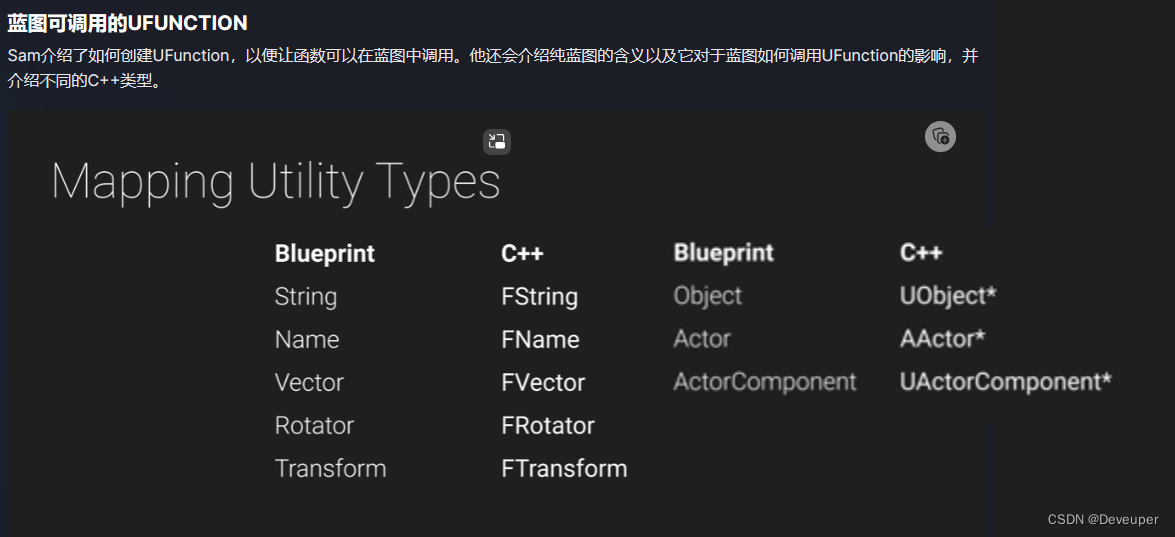
教程链接:示例1:CompleteQuest - 将蓝图转换为C (epicgames.com) 1.常用的引用需要记住,如图所示。 2.蓝图中可以调用C函数,也可以实现C函数 BlueprintImplementableEvent:C只创建,不实现,在蓝图中实现 B…...
——电子琴演奏)
龙芯+RT-Thread+LVGL实战笔记(30)——电子琴演奏
【写在前面】正值期末,笔者工作繁忙,因此本系列教程的更新频率有所放缓,还望订阅本专栏的朋友理解,请勿催更。笔者在此也简要声明几点: 有些硬件模块笔者并没有,如LED点阵、压力传感模块、RFID模块等,因此这些模块的相关任务暂时无法给出经过验证的代码。其实,教程进行…...

Python Process创建进程(2种方法)详解
虽然使用 os.fork() 方法可以启动多个进程,但这种方式显然不适合 Windows,而 Python 是跨平台的语言,所以 Python 绝不能仅仅局限于 Windows 系统,因此 Python 也提供了其他方式在 Windows 下创建新进程。 Python 在 multiproces…...

树莓派4B 使用树莓派官方烧录器烧录ubuntu20.04.5 排坑
问题描述: 使用树莓派官方烧录器烧录ubuntu并且在烧录器中设置了电脑热点,但是无法连接WIFI。重启后也无效。 排坑: 1.首先打开/boot中的network-config,发现烧录器设置的密码是乱码,重新设置; 2.有博主说…...

鸿蒙开发(五)鸿蒙UI开发概览
从用户角度来讲,一个软件拥有好看的UI,那是锦上添花的事情。再精确的算法,再厉害的策略,最终都得通过UI展现给用户并且跟用户交互。那么,本篇一起学习下鸿蒙开发UI基础知识,认识下各种基本控件以及使用方式…...
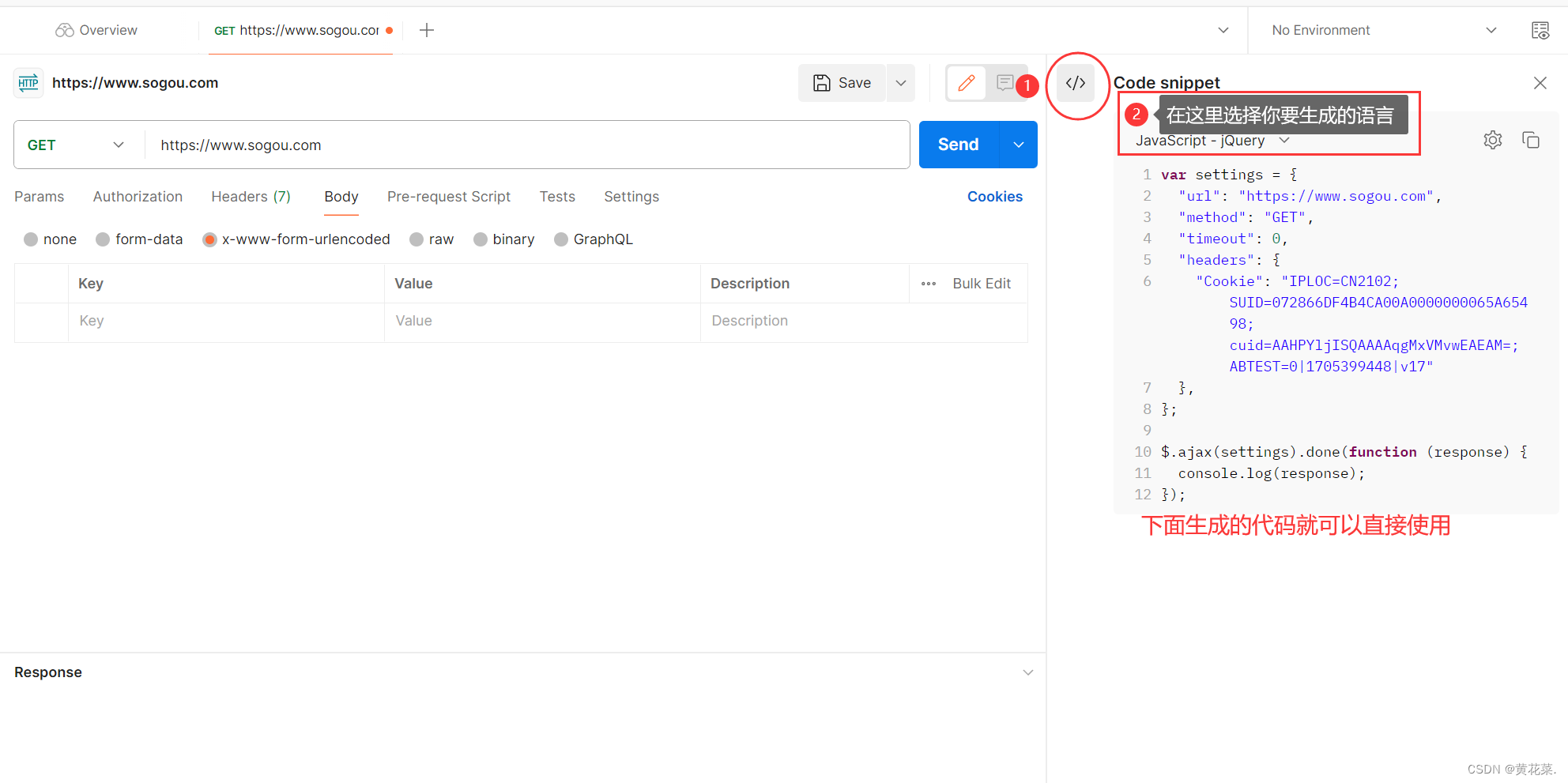
应用层—HTTP详解(抓包工具、报文格式、构造http等……)
文章目录 HTTP1. 抓包工具的使用1.1 配置信息1.2 观察数据 2. 分析 https 抓包结果3. HTTP请求详解3.1 认识 URL3.1.1 URL 基本格式3.1.2 查询字符串 (query string)3.1.3 关于 URL Encode 3.2 认识 http 方法3.2.1 [经典问题] Get 和 Post 主要的区别是什么?&#…...
ISA Server 2006部署网站对比nginx
2024年了,我还是第1次使用ISA Server 。没办法在维护一个非常古老的项目。说到ISA Server可能有小伙们不清楚,但是说到nginx大家应该都知道吧。虽然他们俩定位并不相同,但是本文中提到的需求,他俩是都可以实现。 网上找的到的教程…...

CHAPTER 9: 《DESIGN A WEB CRAWLER》第9章 《设计一个web爬虫》
CHAPTER 9: 《DESIGN A WEB CRAWLER》第九章 设计一个web爬虫 在本章中,我们将重点介绍网络爬虫设计:一种有趣而经典的系统设计 面试问题。 网络爬虫被称为机器人或蜘蛛。它被搜索引擎广泛用于发现网络上的新内容或更新内容。内容可以是网页、图像、视频…...
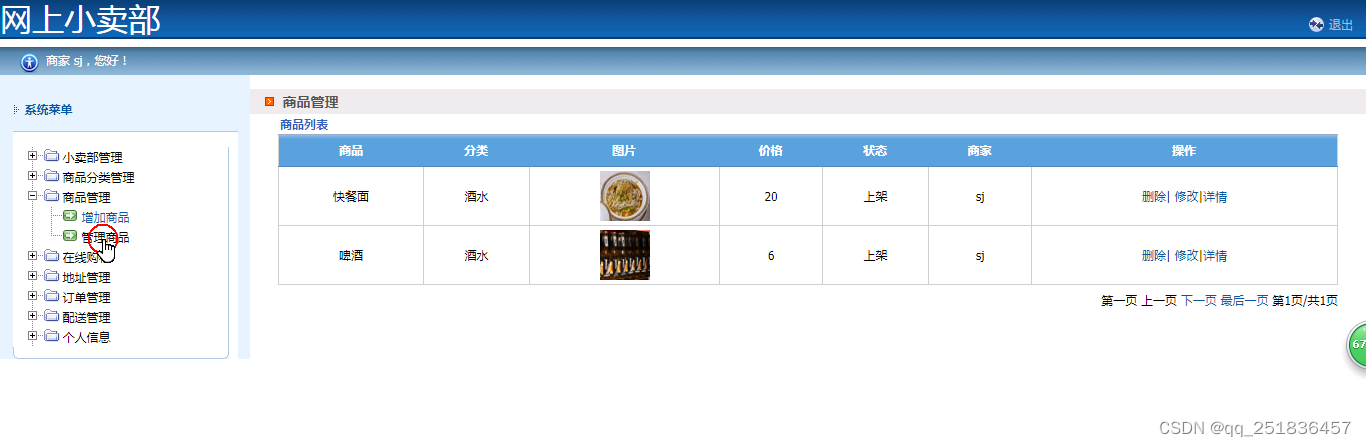
java SSM网上小卖部管理系统myeclipse开发mysql数据库springMVC模式java编程计算机网页设计
一、源码特点 java SSM网上小卖部管理系统是一套完善的web设计系统(系统采用SSM框架进行设计开发,springspringMVCmybatis),对理解JSP java编程开发语言有帮助,系统具有完整的源 代码和数据库,系统主要…...

Java中集合元素的删除
关于集合元素的remove 重点:当集合的结构发生改变时,迭代器必须重新获取,如果还是用以前老的迭代器,会出现异常 java.util.ConcurrentModificationException 重点:在迭代集合元素的过程中,不能调用集合对象…...
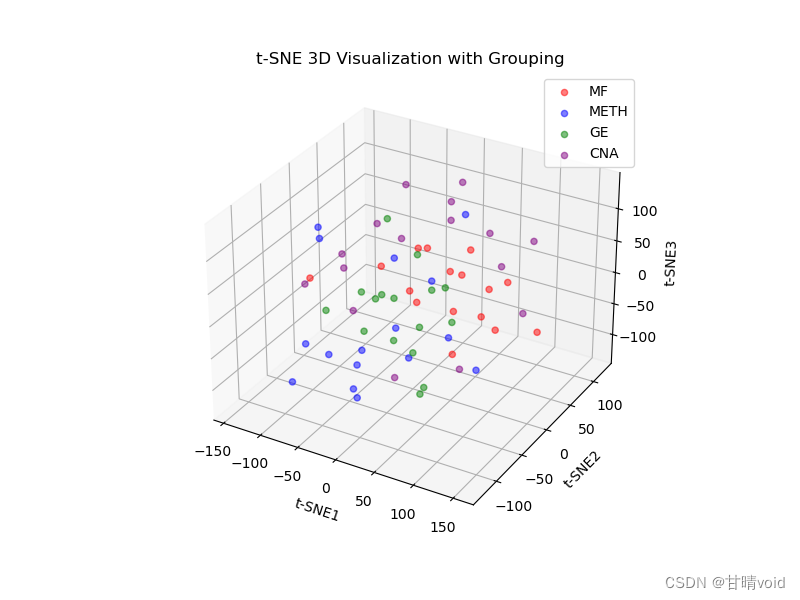
HNU-数据挖掘-实验2-数据降维与可视化
数据挖掘课程实验实验2 数据降维与可视化 计科210X 甘晴void 202108010XXX 文章目录 数据挖掘课程实验<br>实验2 数据降维与可视化实验背景实验目标实验数据集说明实验参考步骤实验过程1.对数据进行初步降维2.使用无监督数据降维方法,比如PCA,I…...

【shell编程入门】正则表达式
正则表达式 特殊字符描述[]方括号表达式,表示匹配的字符集合,例如 [0-9]、[abcde]()标记子表达式起止位置*匹配前面的子表达式零或多次匹配前面的子表达式一或多次?匹配前面的子表达式零或一次\转义字符,除了常用转义外,还有&am…...
高效火情监测,科技助力森林防火【数字地球开放平台】
数字地球开放平台-以卫星遥感为核心的空天信息服务开放平台 (geovisearth.com) 2019年3月30日,四川省凉山州木里县爆发了一场森林火灾,火点位于海拔3800米左右,地形险峻、坡度陡峭、谷深难以抵挡火势。在扑救的过程中,27名森林消防…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
