运行Navicat转储的数据库SQL文件失败
- 报错：1067 - Invalid default value for ‘publish_date’
单独拎出来该建表语句执行，报错一样，都是默认值出错
查看该字段的设计语句
`publish_date` timestamp NOT NULL DEFAULT '0000-00-00 00:00:00' COMMENT '发布时间',
发现该字段的默认值是：‘0000-00-00 00:00:00’，类型为timestamp（时间戳），'0000-00-00 00:00:00’不符合要求，所以更换合适的默认值即可
- 报错：表、视图等does’ not exist
打开运行的sql文件，根据表、视图名查询相关sql，使用该表、视图的sql是不是在创建该表、视图的sql之前，调整一下顺序
相关文章：
运行Navicat转储的数据库SQL文件失败
报错：1067 - Invalid default value for ‘publish_date’ 单独拎出来该建表语句执行，报错一样，都是默认值出错 查看该字段的设计语句 publish_date timestamp NOT NULL DEFAULT 0000-00-00 00:00:00 COMMENT 发布时间, 发现该字段的默认值…...
动静态库的理解、制作、使用。
一.动静态库的理解。 1.什么是库？ 代码是无穷无尽的，当程序猿在写一些项目时，未必所有代码亲历亲为，他们可以在网上寻找大佬写过的一些有关需求的代码，这些代码可以让他们拿过来直接使用，而省去了许多精力…...
【趣味游戏-08】20240123点兵点将点到谁就是谁（列表倒置reverse）
背景需求： 上个月，看到大4班一个孩子在玩“点兵点将点到谁就是谁”的小游戏，他在桌上摆放两排奥特曼卡片，然后点着数“点兵点将点到谁就是谁”，第10次点击的卡片，拿起来与同伴的卡片进行交换。他是从第一排…...
cherry键盘alt+tab无法切换窗口的问题解决
现象： alt 好用， tab好用，tabalt不好用。 原因： 键盘误触了关闭了alttab的功能。 不同的樱桃键盘可能方法不一样，下面是两个方案，本人的键盘是MX6.0 G80 3930红轴，用的方法一解决就了&#…...
「nuxt2配置tailwindcss」nuxt2添加tailwindcss详细步骤！解决版本不对称各种报错～～
运行环境 node和npm使用版本 node v14.21.3 (npm v6.14.18) 1.插件下载 官方文档说明 npm install -D nuxtjs/tailwindcss3.4.3 tailwindcss3.4.1 postcss^8.4.33 autoprefixer10.4.17 2.nuxt.config.js配置 module.exports {// ...buildModules: [nuxtjs/tailwindcss],// …...
1、中级机器学习课程简介
文章目录 1、课程简介2、先决条件 本课程所需数据集夸克网盘下载链接：https://pan.quark.cn/s/9b4e9a1246b2 提取码：uDzP 1、课程简介 欢迎来到机器学习中级课程！ 如果你对机器学习有一些基础，并且希望学习如何快速提高模型质量…...
Mybtisplus对时间字段进行自动填充
一、引入依赖 <!-- mybatis-plus-boot-starter--><dependency><groupId>com.baomidou</groupId><artifactId>mybatis-plus-boot-starter</artifactId><version>3.4.2</version></dependency> 二、配置类 这里我…...
[HTML]Web前端开发技术12（HTML5、CSS3、JavaScript ）——喵喵画网页
希望你开心，希望你健康，希望你幸福，希望你点赞！ 最后的最后，关注喵，关注喵，关注喵，佬佬会看到更多有趣的博客哦！！！ 喵喵喵，你对我真的…...
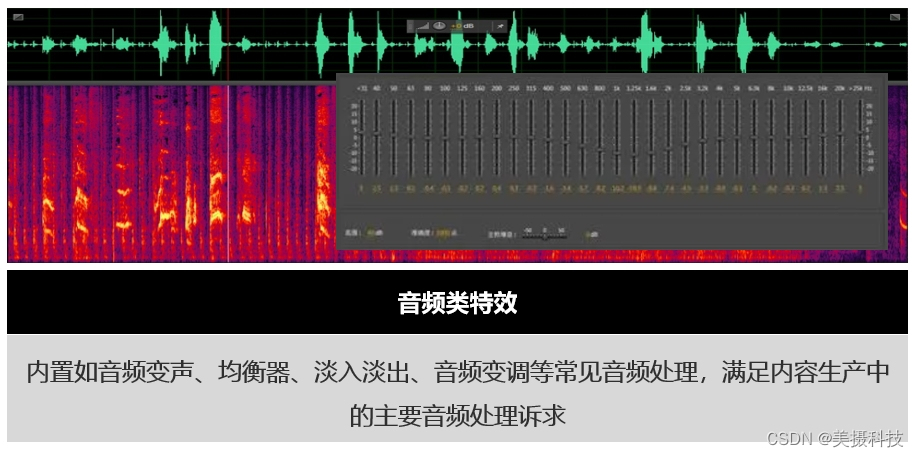
音频特效SDK，满足内容生产的音频处理需求
美摄科技，作为音频处理技术的佼佼者，推出的音频特效SDK，旨在满足企业内容生产中的音频处理需求。这款SDK内置多种常见音频处理功能，如音频变声、均衡器、淡入淡出、音频变调等，帮助企业轻松应对各种音频处理挑战。 一…...
使用vue2写一个太极图，并且点击旋转
下面是我自己写的一个代码，命名有些不规范，大家不要介意。 <template><div class"qq"><div class"app" :style"{ transform: rotateStyle }"><div class"app1"><div class"ap…...
张量计算和操作
一、数据操作 1、基础 import torchx torch.arange(12) # x:tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])x.shape # torch.Size([12])x.numel() # 12x x.reshape(3, 4) # tensor([[ 0, 1, 2, 3], # [ 4, 5, 6, 7], # [ 8, 9, 10, 11]])torch.zeros((2…...
【Spring Boot 3】【JPA】枚举类型持久化
【Spring Boot 3】【JPA】枚举类型持久化 背景介绍开发环境开发步骤及源码工程目录结构总结背景 软件开发是一门实践性科学，对大多数人来说，学习一种新技术不是一开始就去深究其原理，而是先从做出一个可工作的DEMO入手。但在我个人学习和工作经历中，每次学习新技术总是要花…...
SVN 常用命令汇总（2024）
1、前言 1.1、如何检索本文档 使用CSDN自带的“目录”功能进行检索，会更容易查找到自己需要的命令。 1.2、svn常用命令查询：help —— 帮助 在使用过程中，可随时使用help命令查看各常用svn命令： svn help2、检出及更新 2.1、…...
K8S四层代理Service-02
Service的四种类型使用 ClusterIP使用示例Pod里使用service的服务名访问应用 NodePort使用示例 ExternalName使用示例 LoadBalancer K8S支持以下4种Service类型：ClusterIP、NodePort、ExternalName、LoadBalancer 以下是使用4种类型进行Service创建，应对…...
3、非数值型的分类变量
非数值型的分类变量 有很多非数字的数据，这里介绍如何使用它来进行机器学习。 在本教程中，您将了解什么是分类变量，以及处理此类数据的三种方法。 本课程所需数据集夸克网盘下载链接：https://pan.quark.cn/s/9b4e9a1246b2 提取码：uDzP 文章目录 1、简介2、三种方法的使用1…...
国内免费chartGPT网站汇总
https://s.suolj.com - （支持文心、科大讯飞、智谱等国内大语言模型，Midjourney绘画、语音对讲、聊天插件）国内可以直连，响应速度很快 很稳定 https://seboai.github.io - 国内可以直连，响应速度很快 很稳定 http://gp…...
【Alibaba工具型技术系列】「EasyExcel技术专题」实战研究一下 EasyExcel 如何从指定文件位置进行读取数据
实战研究一下 EasyExcel 如何从指定文件位置进行读取数据 EasyExcel的使用背景EasyExcel的时候痛点EasyExcel对比其他框架 EasyExcel的编程模式EasyExcel读取的指定位置导入数据的流程表头校验invokeHeadMap()方法 数据处理invoke()方法 执行中断hasNextdoAfterAllAnalysed()方…...
java.security.InvalidKeyException: Illegal key size错误
出现的问题 最近在对接第三方，涉及获取token鉴权。在本地调试能获取到token，但是在Linux环境上调用就报错：java.security.InvalidKeyException: Illegal key size 与三方沟通 ，排除了是传参和网络的原因；搜索资料发现…...
python脚本，实现监控系统的各项资源
今天的文章涉及到docker的操作和一个python脚本，实现监控网络的流量、CPU使用率、内存使用率和磁盘使用情况。一起先看看效果吧： 这是在控制台中出现的数据，可以很简单的看到我们想要的监控指标。如果实现定时任务和数据的存储、数据的展示&a…...
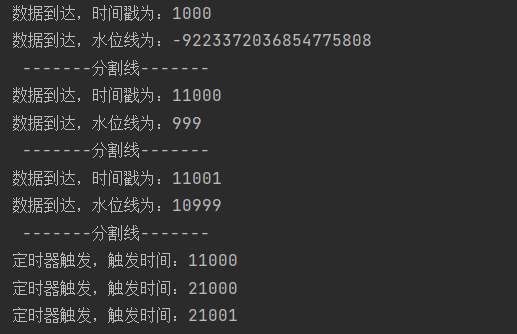
Flink处理函数（2）—— 按键分区处理函数
按键分区处理函数（KeyedProcessFunction）：先进行分区，然后定义处理操作 1.定时器（Timer）和定时服务（TimerService） 定时器（timers）是处理函数中进行时间相关…...
Python｜GIF 解析与构建（5）：手搓截屏和帧率控制
目录 Python｜GIF 解析与构建（5）：手搓截屏和帧率控制 一、引言 二、技术实现：手搓截屏模块 2.1 核心原理 2.2 代码解析：ScreenshotData类 2.2.1 截图函数：capture_screen 三、技术实现&…...
Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块，它提供了一个轻量级的 HTTP 服务器实现，主要用于构建基于 HTTP 的应用程序和服务。 功能介绍： 主要功能 HTTP服务器功能： 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...
12.找到字符串中所有字母异位词
🧠 题目解析 题目描述： 给定两个字符串 s 和 p，找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义： 若两个字符串包含的字符种类和出现次数完全相同，顺序无所谓，则互为…...
图表类系列各种样式PPT模版分享
图标图表系列PPT模版，柱状图PPT模版，线状图PPT模版，折线图PPT模版，饼状图PPT模版，雷达图PPT模版，树状图PPT模版 图表类系列各种样式PPT模版分享：图表系列PPT模板https://pan.quark.cn/s/20d40aa…...
A2A JS SDK 完整教程：快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...
人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
Python 实现 Web 静态服务器（HTTP 协议）
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1）下载安装包2）配置环境变量3）安装镜像4）node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1）使用 http-server2）详解 …...
沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西，但是如果把三者放在一起，它们之间到底什么关系？又有什么联系呢？我不是很明白！！！ 就比如说： 沙箱&#…...
【QT控件】显示类控件
目录 一、Label 二、LCD Number 三、ProgressBar 四、Calendar Widget QT专栏：QT_uyeonashi的博客-CSDN博客 一、Label QLabel 可以用来显示文本和图片. 核心属性如下 代码示例: 显示不同格式的文本 1) 在界面上创建三个 QLabel 尺寸放大一些. objectName 分别…...
ubuntu清理垃圾
windows和ubuntu 双系统，ubuntu 150GB，开发用，基本不装太多软件。但是磁盘基本用完。 1、查看home目录 sudo du -h -d 1 $HOME | grep -v K 上面的命令查看$HOME一级目录大小，发现 .cache 有26GB，.local 有几个GB&am…...