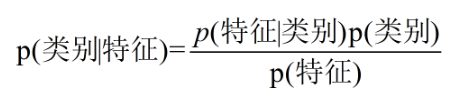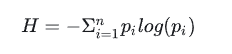人工智能原理实验4(2)——贝叶斯、决策求解汽车评估数据集
🧡🧡实验内容🧡🧡
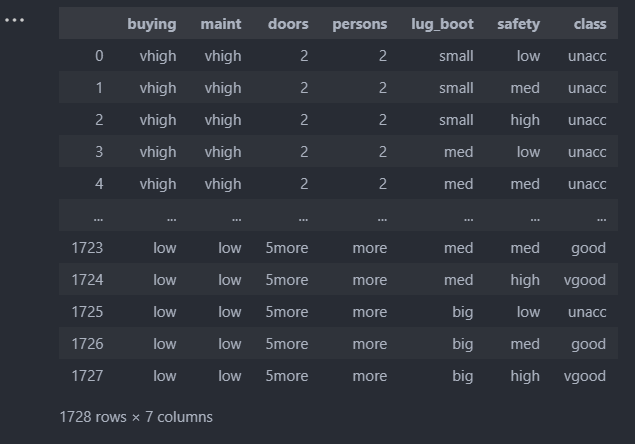
汽车数据集
车子具有 buying,maint,doors,persons,lug_boot and safety六种属性,而车子的好坏分为uncc,ucc,good and vgood四种。
🧡🧡贝叶斯求解🧡🧡
数据预处理
1.转为数字编码
将数据集中的中文分类编码转为数字编码,以便更好地训练。这里采用sklearn的LabelEncoder库进行快速转换。
2.拆分数据集
按7:3的比例拆出训练集和测试集,这里也采用sklearn的train_test_split快速拆分,比手动拆分能更具随机性
3.将dataframe对象转为array
在手动实现的贝叶斯算法类中,通过numpy可以很方便的操纵和计算矩阵格式的数据,因此通过dataframe对象导入数据后,通过df.values将其转为array
朴素贝叶斯原理
- 核心公式:
对于二分类问题,在已知样本特征的情况下,分别求出两个分类的后验概率:P(类别1 | 特征集),P(类别2 | 特征集),选择后验概率最大的分类作为最终预测结果。- 为何需要等式右边?
对于某一特定样本,很难直接计算它的后验概率(左边部分),而根据贝叶斯公式即可转为等式右边的先验概率(P(特征)、P(类别))和条件概率(P(特征 | 类别)),这些可以直接从原有训练样本中求得,其次,由于最后只比较相对大小,因此分母P(特征)在计算过程中可以忽略。- 右边P(特征 | 类别)和P(特征)如何求?
例如,对于car-evalution这个数据集,假设特征只有doors、persons、safety,目标为class。
对于某个样本,它的特征是doors=2、persons=3、safety=low。
则它是unacc的概率是
P(unacc | doors=2、persons=3、safety=low) =
P(doors=2、persons=3、safety=low | unacc) * P(unacc) / P(doors=2、persons=3、safety=low)
对于P(unacc),即原训练样本集中的unacc的频率。
对于P(doors=2、persons=3、safety=low | unacc),并不是直接求原训练样本集中满足unacc条件下,同时为doors=2、persons=3、safety=low的概率,这样由于数据的稀疏性,很容易导致统计频率为0, 因此朴素贝叶斯算法就假设各个特征直接相互独立,即
P(doors=2、persons=3、safety=low | >unacc) = P(doors=2 | unacc)*P(persons=3 |unacc)*P(safety=low | unacc),朴素一词由此而来。
对于P(doors=2、persons=3、safety=low) ,同上述,其等于P(doors=2)*P(persons=3)*P(safety=low)
代码
import pandas as pd
df=pd.read_excel("data/car_data1.xlsx")# ==================数据预处理==================
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
le=LabelEncoder()
for i in df.columns:df[i]=le.fit_transform(df[i])
# df
X=df[df.columns[:-1]]
y=df['class']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=10)#三七开
X_train=X_train.values
X_test=X_test.values
y_train=y_train.values
y_test=y_test.values# ==================朴素贝叶斯==================
import numpy as np
from sklearn.metrics import accuracy_score
class NaiveBayes:def fit(self, X, y):self.X = Xself.y = yself.classes = np.unique(y) # 目标分类名称集:(0 、 1),ex:嫁、不嫁self.prior_probs = {} # 先验概率self.cond_probs = {} # 条件概率# 计算先验概率——分子项 P(类别), ex:P(嫁)、P(不嫁)for c in self.classes:self.prior_probs[c] = np.sum(y == c) / len(y)# 计算条件概率——分子项 P(特征/类别), ex:P(帅、性格好、身高矮、上进 | 嫁)for feature_idx in range(X.shape[1]): # 0....featureNum 表示每一列特征索引,ex:是否帅、是否性格好、身高程度、上不上进self.cond_probs[feature_idx] = {}for c in self.classes:feature_values = np.unique(X[:, feature_idx]) # featureValue1、featureValue2、...ex:帅、不帅self.cond_probs[feature_idx][c] = {}for value in feature_values:idx = (X[:, feature_idx] == value) & (y == c) # [0,1,0,0,0.......]self.cond_probs[feature_idx][c][value] = np.sum(idx) / np.sum(y == c) # ex:P[是否帅][嫁][帅]def predict(self, X_test):pred_label = []pred_scores = []# 对每个测试样本进行预测for x in X_test:posterior_probs = {}# 计算后验概率——P(嫁|帅、性格好、身高矮、上进) 和 P(不嫁|帅、性格好、身高矮、上进)for c in self.classes:posterior_probs[c] = self.prior_probs[c]for feature_idx, value in enumerate(x):if value in self.cond_probs[feature_idx][c]:posterior_probs[c] *= self.cond_probs[feature_idx][c][value]# 选择后验概率最大的类别作为预测结果predicted_class = max(posterior_probs, key=posterior_probs.get) # 获得最大的value对应的keypred_score = posterior_probs[predicted_class] # 获得最大的valuepred_label.append(predicted_class)pred_scores.append(pred_score)return pred_label, pred_scores# ==================训练+预测==================
nb = NaiveBayes()
nb.fit(X_train, y_train)
y_pred, y_scores = nb.predict(X_test)# ==================评估==================
import matplotlib.pyplot as plt
import seaborn as sns# 混淆矩阵
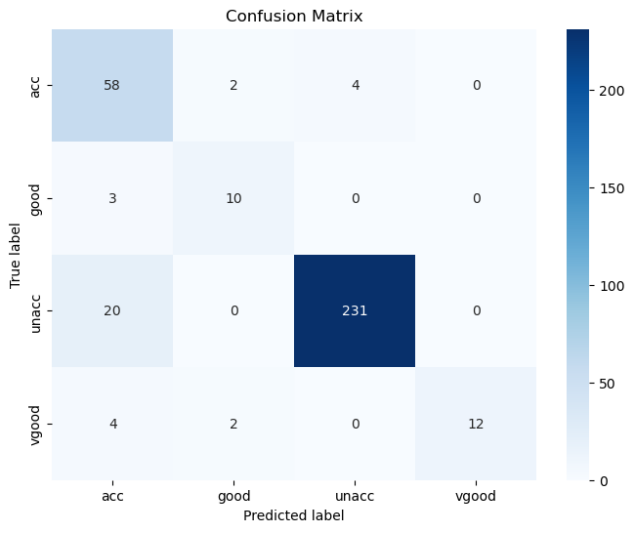
def cal_ConfusialMatrix(y_true_labels, y_pred_labels):cm = np.zeros((4, 4))for i in range(len(y_true_labels)):cm[ y_true_labels[i], y_pred_labels[i] ] += 1plt.figure(figsize=(8, 6))sns.heatmap(cm, annot=True, fmt='g', cmap='Blues', xticklabels=['acc','good','unacc', 'vgood'], yticklabels=['acc','good','unacc', 'vgood'])plt.xlabel('Predicted label')plt.ylabel('True label')plt.title('Confusion Matrix')plt.show()
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("准确率:", accuracy)
y_pred=[int(x) for x in y_pred]
cal_ConfusialMatrix(y_test, y_pred)
结果
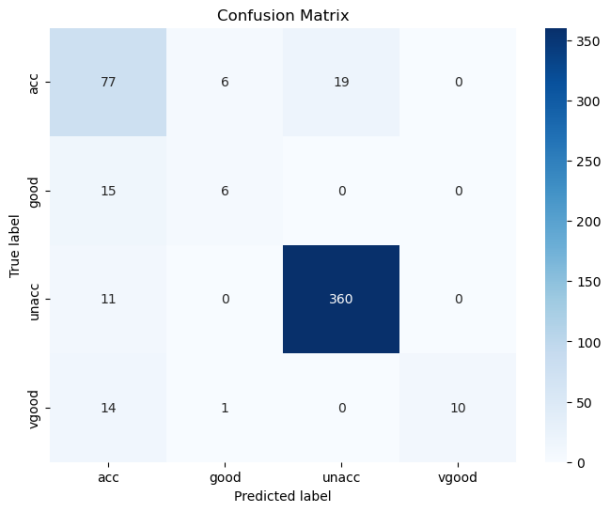
🧡🧡决策树算法求解🧡🧡
数据预处理:
和上述贝叶斯算法中的数据预处理基本一致,这里因为计算信息熵时,要根据信息熵的收敛精度才决定是否跳出递归,经过几次尝试,选择将训练集和测试集8:2的比例拆分,并且random_state=10,避免随机性导致程序死循环。
决策树原理
决策树的决策流程就是从所有输入特征中选择一个特征做为决策的依据,找出一个阈值来决定将其划分到哪一类。
也就是说,创建一个决策树的主要问题在于:
1.决策树中每个节点在哪个维度的特征上面进行划分?
2.被选中的维度的特征具体在哪个值上进行划分?
信息熵的计算公式:
其中n是指数据中一共有n类信息,pi就是指第i类数据所占的比例。
信息熵简单的来说就是表示随机变量不确定度的度量。
熵越大,数据的不确定性就越大。
熵越小,数据的不确定性就越小,也就是越确定。
举个例子
假设我们的数据中一共有三类。每一类所占比例为1/3,那么信息熵就是:
假设我们数据一共有三类,每类所占比例是0,0,1,那么信息熵就是:
(实际上log(0)是不能计算的,定义上不允许,程序中直接置为inf即可)
很显然第二组数据比第一组数据信息熵小,也就是不确定性要少,换句话讲就是更为确定。
我们希望决策树每次划分数据都能让信息熵降低,当划分到最后一个叶子节点里面只有一类数据的时候,信息熵就自然的降为了0,所属的类别就完全确定了。
那么怎样找到一个这样的划分使得划分后的信息熵会降低?对着所有维度的特征来一次搜索就行了。
代码
import pandas as pd
import numpy as np
from collections import Counter
from math import logdf=pd.read_excel("data/car_data1.xlsx")# ==================数据预处理==================
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
le=LabelEncoder()
for i in df.columns:df[i]=le.fit_transform(df[i])
# df
X=df[df.columns[:-1]]
y=df['class']
X = X.astype(float)X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=10) #二八开
X_train=X_train.values
X_test=X_test.values
y_train=y_train.values
y_test=y_test.values# ==================决策树==================
class Node:def __init__(self,x_data, y_label, dimension, value):self.x_data = x_dataself.y_label = y_labelself.dimension = dimensionself.value = valueself.left = Noneself.right = Noneclass DTree:def __init__(self):self.root = Nonedef fit(self,x_train, y_train):def entropy(y_label):counter = Counter(y_label)ent = 0.0for num in counter.values():p = num / len(y_label)ent += -p * log(p)return entdef one_split(x_data, y_label):best_entropy = float('inf')best_dimension = -1best_value = -1for d in range(x_data.shape[1]):sorted_index = np.argsort(x_data[:, d])for i in range(1,len(x_data)):if x_data[sorted_index[i], d] != x_data[sorted_index[i - 1], d]:value = (x_data[sorted_index[i], d] + x_data[sorted_index[i-1], d]) / 2x_left, x_right, y_left, y_right = split(x_data, y_label, d, value)p_left = len(x_left) / len(x_data)p_right = len(x_right) / len(x_data)ent = p_left * entropy(y_left) + p_right * entropy(y_right)if ent < best_entropy:best_entropy = entbest_dimension = dbest_value = valuereturn best_entropy, best_dimension, best_valuedef split(x_data, y_label, dimension, value):"""x_data:输入特征y_label:输入标签类别dimension:选取输入特征的维度索引value:划分特征的数值return 左子树特征,右子树特征,左子树标签,右子树标签"""index_left = (x_data[:,dimension] <= value)index_right = (x_data[:,dimension] > value)return x_data[index_left], x_data[index_right], y_label[index_left], y_label[index_right]def create_tree(x_data, y_label):ent, dim, value = one_split(x_data, y_label)x_left, x_right, y_left, y_right = split(x_data, y_label, dim, value)node = Node(x_data, y_label, dim, value)if ent < 0.3:return nodenode.left = create_tree(x_left, y_left)node.right = create_tree(x_right, y_right)return nodeself.root = create_tree(x_train, y_train)return selfdef predict(self,x_predict):def travel(x_data, node):p = nodeif x_data[p.dimension] <= p.value and p.left:pred = travel(x_data, p.left)elif x_data[p.dimension] > p.value and p.right:pred = travel(x_data, p.right)else:counter = Counter(p.y_label)pred = counter.most_common(1)[0][0]return predy_predict = []for data in x_predict:y_pred = travel(data, self.root)y_predict.append(y_pred)return np.array(y_predict)def score(self,x_test,y_test):y_predict = self.predict(x_test)return np.sum(y_predict == y_test) / len(y_predict), y_predictdef __repr__(self):return "DTree(criterion='entropy')"# =================训练=================
dt = DTree()
dt.fit(X_train, y_train)# ==================评估==================
import matplotlib.pyplot as plt
import seaborn as sns
# 混淆矩阵
def cal_ConfusialMatrix(y_true_labels, y_pred_labels):cm = np.zeros((4, 4))for i in range(len(y_true_labels)):cm[ y_true_labels[i], y_pred_labels[i] ] += 1plt.figure(figsize=(8, 6))sns.heatmap(cm, annot=True, fmt='g', cmap='Blues', xticklabels=['acc','good','unacc', 'vgood'], yticklabels=['acc','good','unacc', 'vgood'])plt.xlabel('Predicted label')plt.ylabel('True label')plt.title('Confusion Matrix')plt.show()
accuracy, y_pred = dt.score(X_test,y_test)
print("准确率:", accuracy)
y_pred=[int(x) for x in y_pred]
cal_ConfusialMatrix(y_test, y_pred)
结果

相关文章:

人工智能原理实验4(2)——贝叶斯、决策求解汽车评估数据集
🧡🧡实验内容🧡🧡 汽车数据集 车子具有 buying,maint,doors,persons,lug_boot and safety六种属性,而车子的好坏分为uncc,ucc,good and vgood四种。 🧡🧡贝叶斯求解🧡🧡…...

算力网络:未来计算资源的驱动力
文章目录 前言一、算力网络的基本概况(一)算力网络的基本概念(二)算力网络研究进展二、运营商的算力网络架构(一)算力网络基础设施构成(二)算力网络编排管理(三)能力开放三、算力网络的优势(一)弹性计算(二)降低成本(三)去中心化四、算力网络的应用场景(一)人…...

java动态导入excel按照表头生成数据库表
1、创建接口接收文件 //controller层 PostMapping("/importExcel1")public void importExcel1(HttpServletRequest request, MultipartFile file) {try {waterMeterService.importExcel1(request,file);} catch (Exception e) {throw new RuntimeException(e);}}//se…...

Java 集合List相关面试题
📕作者简介: 过去日记,致力于Java、GoLang,Rust等多种编程语言,热爱技术,喜欢游戏的博主。 📗本文收录于java面试题系列,大家有兴趣的可以看一看 📘相关专栏Rust初阶教程、go语言基…...
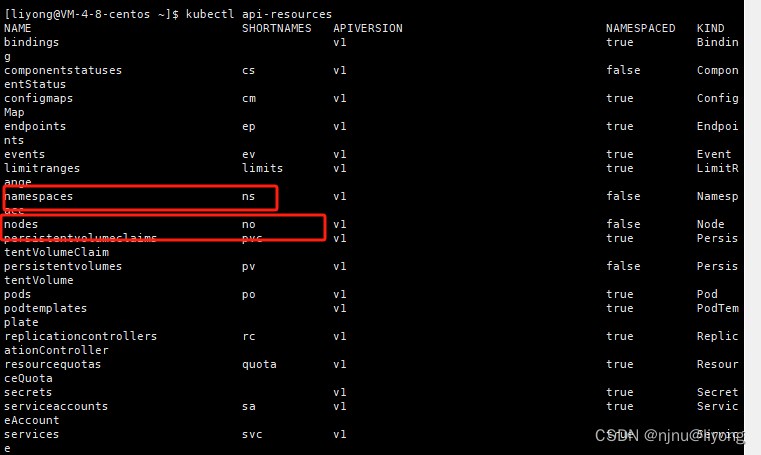
k8s-基础知识(Pod,Deployment,ReplicaSet)
k8s职责 自动化容器部署和复制随时扩展或收缩容器容器分组group,并且提供容器间的负载均衡实时监控,即时故障发现,自动替换 k8s概念及架构 pod pod是容器的容器,可以包含多个container pod是k8s最小可部署单元,容器…...

matlab查看源代码
matlab函数源代码-查看 CtrlD 最简单方便的一种方法,鼠标划中函数名,按CTRLD即可打开函数的m文件...

【数据库学习】PostgreSQL优化
1,思路 2,执行计划 explain sql语句; #查看执行计划。也可以使用navicat的解释功能查看。结果说明: QUERY PLAN Index Scan using tenk1_unique1 on tenk1 (cost0.00..10.01 rows1 width244) --Index 使用索引 --cost&#x…...

微信小程序分页加载功能,结合后端实现上拉底部加载下一页数据,数据加载中和暂无数据提示
🤵 作者:coderYYY 🧑 个人简介:前端程序媛,目前主攻web前端,后端辅助,其他技术知识也会偶尔分享🍀欢迎和我一起交流!🚀(评论和私信一般会回&#…...

idea 打包跳过测试
IDEA操作 点击蓝色的小球 手动命令 mvn clean package -Dmaven.test.skiptrue...

python sqlite3 线程池封装
1. 封装 sqlite3 1.1. 依赖包引入 # -*- coding: utf-8 -*- #import os import sys import datetime import loggingimport sqlite31.2. 封装类 class SqliteTool(object):#def __init__(self, host, port, user, password, database):def __init__(self, host, database):s…...

亚马逊运营:如何通过自养号测评有效防关联,避免砍单
店铺安全对于跨境电商卖家至关重要,它是我们业务稳定运营的基础。一旦店铺遭到亚马逊的封禁,往往意味着巨大的损失。因此,合规运营已经成为了卖家们的共识。然而,许多卖家可能会因为一些看似微小的失误,导致店铺被关联…...

winfrom图像加速渲染时图像不显示
winform中加入这段代码,即使不调用也会起作用;当图像不显示时,可以注释掉这段代码...

Redash 默认key漏洞(CVE-2021-41192)复现
Redash是以色列Redash公司的一套数据整合分析解决方案。该产品支持数据整合、数据可视化、查询编辑和数据共享等。 Redash 10.0.0及之前版本存在安全漏洞,攻击者可利用该漏洞来使用已知的默认值伪造会话。 1.漏洞级别 中危 2.漏洞搜索 fofa "redash"…...

Git学习笔记:3 git tag命令
文章目录 git tag 基本用法1. 创建标签2. 查看标签3. 删除标签4. 推送标签到远程仓库5. 检出标签 普通提交和标签的区别1. 提交(Commit)2. 标签(Tag) git tag 基本用法 git tag 是 Git 中用于管理和操作标签(tag&…...

10年软件测试经验,该有什么新的职业规划?
个人觉得,最关键是识别个人的兴趣和长期目标,以及市场需求,制定符合自己职业发展的规划,列了几个常见的方向: 1. 技术深化 专业领域专长:在某一测试领域(如自动化测试、性能测试、安全测试等&am…...
重构改善既有代码的设计-学习(四):简化条件逻辑
1、分解条件表达式(Decompose Conditional) 可以将大块代码分解为多个独立的函数,根据每个小块代码的用途,为分解而得的新函数命名。对于条件逻辑,将每个分支条件分解成新函数还可以带来更多好处:可以突出条…...

【代码---利用一个小程序,读取文件夹中图片,将其合成为一个视频】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言程序详细说明总结 前言 提示:这里可以添加本文要记录的大概内容: 创建一个程序将图像合成为视频通常需要使用图像处理和视频编码库。 …...

MVC 和 MVVM的区别
MVC: M(model数据)、V(view视图),C(controlle控制器) 缺点是前后端无法独立开发,必须等后端接口做好了才可以往下走; 前端没有自己的数据中心,太…...
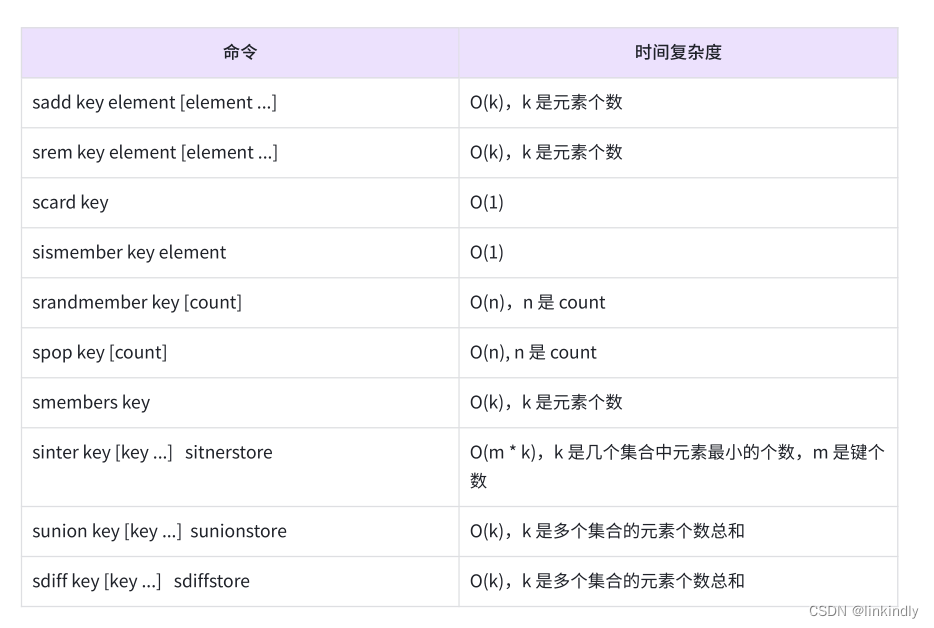
redis—Set集合
目录 前言 1.常见命令 2.使用场景 前言 集合类型也是保存多个字符串类型的元素的,但和列表类型不同的是,集合中1)元素之间是无序的2)元素不允许重复,如图2-24所示。一个集合中最多可以存储22 - 1个元素。Redis 除了支持集合内的增删查改操…...
【jetson笔记】vscode远程调试
vscode安装插件 vscode安装远程插件Remote-SSH 安装完毕点击左侧远程资源管理器 打开SSH配置文件 添加如下内容,Hostname为jetson IP,User为登录用户名需替换为自己的 Host aliasHostName 192.168.219.57User jetson配置好点击连接,控制台输…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...