瑞_数据结构与算法_二叉搜索树
文章目录
- 1 什么是二叉搜索树
- 1.1 二叉搜索树的特征
- 1.2 前驱后继
- 2 二叉搜索树的Java实现
- 2.1 定义二叉搜索树节点类BSTNode
- 泛型key改进
- 2.2 实现查找方法get(int key)
- 递归实现
- 非递归实现 ★
- 非递归实现 泛型key版本
- 2.3 实现查找最小方法min()
- 递归实现
- 非递归实现 ★
- 2.4 实现查找最大方法max()
- 递归实现
- 非递归实现 ★
- 2.5 实现新增方法put(int key, Object value)
- 递归实现
- 非递归实现 ★
- 2.6 实现查找关键字的前任值predecessor(int key)
- 2.7 查找关键字的后任值successor(int key)
- 2.8 根据关键字删除remove(int key)
- 非递归实现 ★
- 递归实现
- 3 二叉搜索树——范围查询
- 3.1 找所有小于索引的值less(int key)
- 3.2 找所有大于索引的值greater(int key)
- 3.3 找范围值between(int key1, int key2)
- 3.3 小结
🙊前言:本文章为瑞_系列专栏之《数据结构与算法》的二叉搜索树篇。由于博主是从B站黑马程序员的《数据结构与算法》学习到的相关知识,所以本系列专栏主要针对该课程进行笔记总结和拓展,文中的部分原理及图解也是来源于黑马提供的资料。本文仅供大家交流、学习及研究使用,禁止用于商业用途,违者必究!

1 什么是二叉搜索树
二叉搜索树最早是由Bernoulli兄弟在18世纪中提出的,但是真正推广和应用该数据结构的是1960年代的D.L. Gries。他的著作《The Science of Programming》中详细介绍了二叉搜索树的实现和应用。
在计算机科学的发展中,二叉搜索树成为了一种非常基础的数据结构,被广泛应用在各种领域,包括搜索、排序、数据库索引等。随着计算机算力的提升和对数据结构的深入研究,二叉搜索树也不断被优化和扩展,例如AVL树、红黑树等。
1.1 二叉搜索树的特征
二叉搜索树(也称二叉排序树)是符合下面特征的二叉树:
- 树节点增加 key 属性,用来比较谁大谁小,key 不可以重复
- 对于任意一个树节点,它的 key 比左子树的 key 都大,同时也比右子树的 key 都小,例如下图所示:

轻易看出要查找 7 (从根开始)自然就可应用二分查找算法,只需三次比较
- 与 4 比,较之大,向右找
- 与 6 比,较之大,继续向右找
- 与 7 比,相等,即找到
查找的时间复杂度与树高相关,插入、删除也是如此。
- 如果这棵树长得还不赖(左右平衡)如上图,那么时间复杂度均是 O ( log N ) O(\log{N}) O(logN)
- 当然,这棵树如果长得丑(左右高度相差过大)如下图,那么这时是最糟的情况(链表),时间复杂度是 O ( N ) O(N) O(N)

注:
- 二叉搜索树 - 英文 binary search tree,简称 BST
- 二叉排序树 - 英文 binary ordered tree 或 binary sorted tree
二叉树的相关知识可以参考博客:《瑞_数据结构与算法_二叉树》
二分查找的相关知识可以参考博客:瑞_数据结构与算法_二分查找
1.2 前驱后继
- 前驱值(前任值):找到一个离该节点最近且比该节点存储值小的值
- 后继值(后任值):找到一个离该节点最近且比该节点存储值大的值
2 二叉搜索树的Java实现
以简单实现为主,主要是学习其思想,和Java中的Map集合实现的思维类似,通过key查找value
内部节点类BSTNode中含有属性:
- 索引
- 存储值
- 左孩子
- 右孩子属性
BSTTree二叉搜索树类含有方法:
- 查找关键字对应的值get(int key)
- 查找最小关键字对应值min()
- 查找最大关键字对应值max()
- 存储关键字和对应值put(int key, Object value)
- 查找关键字的前任值predecessor(int key)
- 查找关键字的后任值successor(int key)
- 根据关键字删除remove(int key)
2.1 定义二叉搜索树节点类BSTNode
BSTNode即二叉搜索树节点类(内部类),含有索引、存储值、左孩子、右孩子属性,由于是简单实现,索引定义基本数据类型(若希望任意类型作为 key,则后续可以将其设计为 Comparable 接口)
/*** Binary Search Tree 二叉搜索树** @author LiaoYuXing-Ray* @version 1.0* @createDate 2024/1/24 19:27**/
public class BSTTree {/*** 根节点*/BSTNode root;static class BSTNode {// 索引,比较值int key;// 该节点的存储值Object value;// 左孩子BSTNode left;// 右孩子BSTNode right;public BSTNode(int key) {this.key = key;}public BSTNode(int key, Object value) {this.key = key;this.value = value;}public BSTNode(int key, Object value, BSTNode left, BSTNode right) {this.key = key;this.value = value;this.left = left;this.right = right;}}}
泛型key改进
使用泛型上限语法,让泛型的Key继承Comparable接口,使其能够进行大小比较。改进后代码如下(含get方法):
/*** 二叉搜索树, 泛型 key 版本*/
public class BSTTree<K extends Comparable<K>, V> {static class BSTNode<K, V> {K key;V value;BSTNode<K, V> left;BSTNode<K, V> right;public BSTNode(K key) {this.key = key;}public BSTNode(K key, V value) {this.key = key;this.value = value;}public BSTNode(K key, V value, BSTNode<K, V> left, BSTNode<K, V> right) {this.key = key;this.value = value;this.left = left;this.right = right;}}BSTNode<K, V> root;public V get(K key) {if (key == null) {return null;}BSTNode<K, V> node = root;while (node != null) {int result = key.compareTo(node.key);if (result < 0) {node = node.left;} else if (result > 0) {node = node.right;} else {return node.value;}}return null;}
}瑞:此处泛型没有定义为T而定义K,是因为K、V迎合map集合中的key,value,容易理解
2.2 实现查找方法get(int key)
get(int key)方法通过关键字查找对应的值
递归实现
get(int key)方法是通过key索引关键字查找对应的值,可以使用递归查找
/*** <h3>查找关键字对应的值</h3>** @param key 关键字* @return 关键字对应的值*/public Object get(int key) {return doGet(root, key);}/*** 私有 - 封装BSTNode参数,外部只需要调用get(int key)方法即可,不用关心具体细节** @param node 根节点* @param key 索引关键字 * @return java.lang.Object 关键字对应的值* @author LiaoYuXing-Ray 2024/1/24 19:53**/private Object doGet(BSTNode node, int key) {if (node == null) {return null; // 没找到}if (key < node.key) {return doGet(node.left, key); // 向左找} else if (node.key < key) {return doGet(node.right, key); // 向右找} else {return node.value; // 找到了}}
瑞:该递归实现是尾递归
尾递归是一种特殊形式的递归,它的特点是在函数的最后一步调用自身,并且不需要保留外层函数的调用记录。
注意区别伪递归,伪递归通常指的是使用迭代实现的递归算法,它们在逻辑上模拟了递归的过程,但实际上并不通过函数调用自身来实现。
尾递归的特点:
- 在函数的最后一步调用自身,不保留外层函数的调用记录。
- 可以仅使用常量级的栈空间,与迭代过程类似。
- 有着与循环同样优秀的计算性能。
伪递归的特点:- 使用迭代来模拟递归的逻辑。
- 不涉及实际的函数自我调用。
- 通常用于那些不支持尾递归优化的编程语言中,以减少内存消耗。
方法测试代码如下:
/*** Binary Search Tree 二叉搜索树** @author LiaoYuXing-Ray* @version 1.0* @createDate 2024/1/24 19:27**/
public class BSTTree {/*** 根节点*/BSTNode root;static class BSTNode {// 索引,比较值int key;// 该节点的存储值Object value;// 左孩子BSTNode left;// 右孩子BSTNode right;public BSTNode(int key) {this.key = key;}public BSTNode(int key, Object value) {this.key = key;this.value = value;}public BSTNode(int key, Object value, BSTNode left, BSTNode right) {this.key = key;this.value = value;this.left = left;this.right = right;}}/*** <h3>查找关键字对应的值</h3>* 递归实现** @param key 关键字* @return 关键字对应的值*/public Object get(int key) {return doGet(root, key);}/*** 私有 - 封装BSTNode参数,外部只需要调用get(int key)方法即可,不用关心具体细节** @param node 根节点* @param key 索引关键字* @return java.lang.Object 关键字对应的值* @author LiaoYuXing-Ray 2024/1/24 19:53**/private Object doGet(BSTNode node, int key) {if (node == null) {return null; // 没找到}if (key < node.key) {return doGet(node.left, key); // 向左找} else if (node.key < key) {return doGet(node.right, key); // 向右找} else {return node.value; // 找到了}}public static void main(String[] args) {/*4/ \2 6/ \ / \1 3 5 7*/BSTNode n1 = new BSTNode(1, "Ray1");BSTNode n3 = new BSTNode(3, "Ray3");BSTNode n2 = new BSTNode(2, "Ray2", n1, n3);BSTNode n5 = new BSTNode(5, "Ray5");BSTNode n7 = new BSTNode(7, "Ray7");BSTNode n6 = new BSTNode(6, "Ray6", n5, n7);BSTNode root = new BSTNode(4, "Ray4", n2, n6);BSTTree tree = new BSTTree();tree.root = root;for (int i = 0; i <= 8; i++) {System.out.println(tree.get(i));}}}
运行结果如下,找不到索引为0和8的元素存储值,而1-7都能找到,符合预期:
nullRay1Ray2Ray3Ray4Ray5Ray6Ray7null
非递归实现 ★
由于之前使用的是尾递归实现,而尾递归转换成迭代法是非常容易的,性能上也能有所提升,所以一般情况下,如果使用尾递归都会转化为迭代法。
/*** <h3>查找关键字对应的值</h3>* 非递归实现** @param key 关键字* @return 关键字对应的值*/public Object get(int key) {BSTNode node = root;while (node != null) {if (key < node.key) {// 向左找node = node.left;} else if (node.key < key) {// 向右找node = node.right;} else {// 找到return node.value;}}// 没找到return null;}
瑞:测试用例可以使用同一个,同样能通过,且性能更佳。
非递归实现 泛型key版本
如果希望让除 int 外更多的类型能够作为 key,一种方式是 key 必须实现 Comparable 接口。
由于compareTo方法返回-1,表示key < node.key,0表示key == node.key,1表示key > node.key,所以改进后代码如下:
public V get(K key) {BSTNode<K, V> node = root;while (node != null) {/*-1 key < p.key0 key == p.key1 key > p.key*/int result = key.compareTo(node.key);if (result < 0) {node = node.left;} else if (result > 0) {node = node.right;} else {return node.value;}}return null;}
还有一种做法不要求 key 实现 Comparable 接口,而是在构造 Tree 时把比较规则作为 Comparator 传入,将来比较 key 大小时都调用此 Comparator 进行比较,这种做法可以参考 Java 中的 java.util.TreeMap
方法测试代码如下:
/*** 二叉搜索树, 泛型 key 版本*/
public class BSTTree<K extends Comparable<K>, V> {static class BSTNode<K, V> {K key;V value;BSTNode<K, V> left;BSTNode<K, V> right;public BSTNode(K key) {this.key = key;}public BSTNode(K key, V value) {this.key = key;this.value = value;}public BSTNode(K key, V value, BSTNode<K, V> left, BSTNode<K, V> right) {this.key = key;this.value = value;this.left = left;this.right = right;}}BSTNode<K, V> root;public V get(K key) {if (key == null) {return null;}BSTNode<K, V> node = root;while (node != null) {/*-1 key < node.key0 key == node.key1 key > node.key*/int result = key.compareTo(node.key);if (result < 0) {node = node.left;} else if (result > 0) {node = node.right;} else {return node.value;}}return null;}public static void main(String[] args) {BSTNode<String,String> n1 = new BSTNode<>("a", "RayA");BSTNode<String,String> n3 = new BSTNode<>("c", "RayC");BSTNode<String,String> n2 = new BSTNode<>("b", "RayB", n1, n3);BSTNode<String,String> n5 = new BSTNode<>("e","RayE");BSTNode<String,String> n7 = new BSTNode<>("g","RayG");BSTNode<String,String> n6 = new BSTNode<>("f", "RayF", n5, n7);BSTNode<String,String> root = new BSTNode<>("d", "RayD", n2, n6);BSTTree<String,String> tree = new BSTTree<>();tree.root = root;System.out.println(tree.get("a"));System.out.println(tree.get("b"));System.out.println(tree.get("c"));System.out.println(tree.get("d"));System.out.println(tree.get("e"));System.out.println(tree.get("f"));System.out.println(tree.get("g"));System.out.println(tree.get("h"));}
}运行结果如下,符合预期:
RayARayBRayCRayDRayERayFRayGnull
2.3 实现查找最小方法min()
min()方法查找最小关键字key的对应存储值
递归实现
根据二叉搜索树的特征,树中最左的节点即为最小索引(关键字),即向左走到头即可,所以只要左孩子为null,即找到最小关键字,使用递归实现的代码就非常简单,如下:
/*** <h3>查找最小关键字对应值</h3>* 递归实现** @return 关键字对应的值*/public Object min() {return doMin(root);}public Object doMin(BSTNode node) {if (node == null) {return null;}// 左边已走到头if (node.left == null) {return node.value;}return doMin(node.left);}
非递归实现 ★
由于之前使用的是尾递归实现,所以下面转化为迭代法,代码如下:
/*** <h3>查找最小关键字对应值</h3>* 非递归实现** @return 关键字对应的值*/public Object min() {return min(root);}private Object min(BSTNode node) {if (node == null) {return null;}BSTNode p = node;// 左边未走到头while (p.left != null) {p = p.left;}return p.value;}
方法测试代码如下:
public static void main(String[] args) {/*4/ \2 6/ \ / \1 3 5 7*/BSTNode n1 = new BSTNode(1, "Ray1");BSTNode n3 = new BSTNode(3, "Ray3");BSTNode n2 = new BSTNode(2, "Ray2", n1, n3);BSTNode n5 = new BSTNode(5, "Ray5");BSTNode n7 = new BSTNode(7, "Ray7");BSTNode n6 = new BSTNode(6, "Ray6", n5, n7);BSTNode root = new BSTNode(4, "Ray4", n2, n6);BSTTree tree = new BSTTree();tree.root = root;System.out.println(tree.min()); }
运行结果如下,查找到最小(最左节点)索引key为1的存储值Ray1,符合预期:
Ray1
2.4 实现查找最大方法max()
max()方法查找最大关键字key的对应存储值
递归实现
与min()方法实现的思想类似,树中最右的节点即为最大索引(关键字),即向右走到头即可,所以只要右孩子为null,即找到最大关键字,使用递归实现的代码如下:
/*** <h3>查找最大关键字对应值</h3>* 递归实现** @return 关键字对应的值*/public Object max() {return doMax(root);}public Object doMax(BSTNode node) {if (node == null) {return null;}// 右边已走到头if (node.right == null) {return node.value;}return doMax(node.right);}
非递归实现 ★
由于之前使用的是尾递归实现,所以下面转化为迭代法,代码如下:
/*** <h3>查找最大关键字对应值</h3>** @return 关键字对应的值*/public Object max() {return max(root);}private Object max(BSTNode node) {if (node == null) {return null;}BSTNode p = node;while (p.right != null) {p = p.right;}return p.value;}方法测试代码如下:
public static void main(String[] args) {BSTNode n1 = new BSTNode(1, "Ray1");BSTNode n3 = new BSTNode(3, "Ray3");BSTNode n2 = new BSTNode(2, "Ray2", n1, n3);BSTNode n5 = new BSTNode(5, "Ray5");BSTNode n7 = new BSTNode(7, "Ray7");BSTNode n6 = new BSTNode(6, "Ray6", n5, n7);BSTNode root = new BSTNode(4, "Ray4", n2, n6);BSTTree tree = new BSTTree();tree.root = root;System.out.println(tree.max());}
运行结果如下,查找到最大(最右节点)索引key为7的存储值Ray7,符合预期:
Ray7
2.5 实现新增方法put(int key, Object value)
新增put(int key, Object value)方法存储关键字和对应值,和Java中的Map的put方法类似,分为两种情况:
1️⃣ key在整个树中已经存在,新增操作变为更新操作,将旧的值替换为新的值
2️⃣ key在整个树中未存在,执行新增操作,将key value添加到树中
递归实现
递归实现思路如下:
- 若找到 key,走 else 更新找到节点的值
- 若没找到 key,走第一个 if,创建并返回新节点
- 返回的新节点,作为上次递归时 node 的左孩子或右孩子
- 缺点是,会有很多不必要的赋值操作
/*** <h3>存储关键字和对应值</h3>* 递归实现** @param key 关键字* @param value 值*/public void put(int key, Object value) {root = doPut(root, key, value);}private BSTNode doPut(BSTNode node, int key, Object value) {if (node == null) {return new BSTNode(key, value);}if (key < node.key) {node.left = doPut(node.left, key, value);} else if (node.key < key) {node.right = doPut(node.right, key, value);} else {node.value = value;}return node;}
非递归实现 ★
查找逻辑和get方法的逻辑基本一样,区别是如果查找到值则更新node.value = value;,没查找到则新增。在新增时为了防止频繁的更新操作,添加parent父节点,判断新增节点是父节点的左孩子还是右孩子,然后再新增,代码如下:
/*** <h3>存储关键字和对应值</h3>* 非递归实现** @param key 关键字* @param value 值*/public void put(int key, Object value) {BSTNode node = root;BSTNode parent = null; // 父节点while (node != null) {parent = node;if (key < node.key) {node = node.left;} else if (node.key < key) {node = node.right;} else {// 1. key 存在则更新node.value = value;return;}}// 2. key 不存在则新增,判断新节点是父节点的左孩子还是右孩子// parent 为空代表树为空的情况,那新增节点就是根节点if (parent == null) {root = new BSTNode(key, value);}// 新增节点为左孩子else if (key < parent.key) {parent.left = new BSTNode(key, value);}// 新增节点为右孩子else {parent.right = new BSTNode(key, value);}}
测试代码:
public static void main(String[] args) {/*4/ \2 6/ \ / \1 3 5 7*/BSTNode n1 = new BSTNode(1, "Ray1");BSTNode n3 = new BSTNode(3, "Ray3");BSTNode n2 = new BSTNode(2, "Ray2", n1, n3);BSTNode n5 = new BSTNode(5, "Ray5");BSTNode n7 = new BSTNode(7, "Ray7");BSTNode n6 = new BSTNode(6, "Ray6", n5, n7);BSTNode root = new BSTNode(4, "Ray4", n2, n6);BSTTree createTree = new BSTTree();createTree.root = root;BSTTree tree = new BSTTree();tree.put(4, new Object());tree.put(2, new Object());tree.put(6, new Object());tree.put(1, new Object());tree.put(3, new Object());tree.put(5, new Object());tree.put(7, new Object());System.out.println(createTree == tree);tree.put(1, "Ray486");System.out.println(tree.get(1).equals("Ray486"));}
两树的key一致但输出false,说明不是同样的树,索引1的存储值被成功替换,均符合预期,测试结果如下:
falsetrue
2.6 实现查找关键字的前任值predecessor(int key)
回顾跳转前驱后继
一个节点的前驱(前任)节点是指:比它小的节点中,最大的那个
一个节点的后继(后任)节点是指:比它大的节点中,最小的那个

例如上图中
- 1 没有前驱,后继是 2
- 2 前驱是 1,后继是 3
- 3 前驱是 2,后继是 4
想要找到二叉搜索树的某节点的前驱后继节点,简单(但不高效)的办法是中序遍历,即可获得排序结果,此时很容易找到前驱后继。因为使用中序遍历后二叉搜索树的值就是升序的,有了升序排序,前驱后继节点就很好找。但是,由于中序遍历的性能不高,所以不推荐使用。
要效率更高,需要研究一下规律,找前驱分成以下 2 种情况:
1️⃣节点 有 左子树,此时前驱节点就是左子树的最大值,图中属于这种情况的有:
- 2 的前驱是1
- 4 的前驱是 3
- 6 的前驱是 5
- 7 的前驱是 6
2️⃣节点 没有 左子树,若离它最近的祖先自从左而来,此祖先即为前驱,如:
- 3 的祖先 2 自左而来,前驱 2
- 5 的祖先 4 自左而来,前驱 4
- 8 的祖先 7 自左而来,前驱 7
- 1 没有这样的祖先,前驱 null
瑞:祖先不止是父节点,也可以是父节点的父节点,父节点的的父节点的父节点…
对于情况2,只需要添加一个指针,记录最近一个自左而来的祖先即可,实现代码如下:
/*** <h3>查找关键字的前任值</h3>** @param key 关键字* @return 前任值*/public Object predecessor(int key) {BSTNode p = root;// 自左而来的祖先BSTNode ancestorFromLeft = null;while (p != null) {if (key < p.key) {p = p.left;} else if (p.key < key) {// 记录自左而来的祖先ancestorFromLeft = p;p = p.right;} else {break;}}// 没找到节点if (p == null) {return null;}// 找到节点 情况1:节点有左子树,此时前任就是左子树的最大值if (p.left != null) {return max(p.left);}// 找到节点 情况2:节点没有左子树,若离它最近的、自左而来的祖先就是前任return ancestorFromLeft != null ?ancestorFromLeft.value : null;}
2.7 查找关键字的后任值successor(int key)
回顾跳转前驱后继
一个节点的前驱(前任)节点是指:比它小的节点中,最大的那个
一个节点的后继(后任)节点是指:比它大的节点中,最小的那个

与前驱类似找后继也分成 2 种情况:
1️⃣节点有右子树,此时后继节点即为右子树的最小值,如:
- 2 的后继 3
- 3 的后继 4
- 5 的后继 6
- 7 的后继 8
2️⃣节点没有右子树,若离它最近的祖先自右而来,此祖先即为后继,如:
- 1 的祖先 2 自右而来,后继 2
- 4 的祖先 5 自右而来,后继 5
- 6 的祖先 7 自右而来,后继 7
- 8 没有这样的祖先,后继 null
代码实现和前任类似,如下:
/*** <h3>查找关键字的后任值</h3>** @param key 关键字* @return 后任值*/public Object successor(int key) {BSTNode p = root;// 自右而来的祖先BSTNode ancestorFromRight = null;while (p != null) {if (key < p.key) {// 记录自右而来的祖先ancestorFromRight = p;p = p.left;} else if (p.key < key) {p = p.right;} else {break;}}// 没找到节点if (p == null) {return null;}// 找到节点 情况1:节点有右子树,此时后任就是右子树的最小值if (p.right != null) {return min(p.right);}// 找到节点 情况2:节点没有右子树,若离它最近的、自右而来的祖先就是后任return ancestorFromRight != null ?ancestorFromRight.value : null;}
2.8 根据关键字删除remove(int key)
删除remove(int key)方法需要考虑的情况较多。要删除某节点(称为 D),必须先找到被删除节点的父节点,这里称为 Parent,具体情况如下:
- 删除节点没有左孩子,将右孩子托孤给 Parent
- 删除节点没有右孩子,将左孩子托孤给 Parent
- 删除节点左右孩子都没有,已经被涵盖在情况1、情况2 当中,把 null 托孤给 Parent
- 删除节点左右孩子都有,可以将它的后继节点(称为 S)托孤给 Parent,设 S 的父亲为 SP,又分两种情况
- SP 就是被删除节点,此时 D 与 S 紧邻,只需将 S 托孤给 Parent
- SP 不是被删除节点,此时 D 与 S 不相邻,此时需要将 S 的后代托孤给 SP,再将 S 托孤给 Parent
删除本身很简单,只要通过索引查找到该节点删除即可,但是,由于需要料理后事,所以想要做好删除操作,需要处理好“托孤”操作。
非递归实现 ★
情况3走情况1或者情况2的逻辑都是可以的,所以不用管,主要是情况4的第二种子情况(删除和后继不相邻),需要处理好该情况下要删除节点的后任的托孤(利用后继节点不会有左孩子,如果有左孩子,那就不会是最小值,所以后继不可能有左孩子),再将后继节点托孤给被删除节点的父节点,代码如下:
/*** <h3>根据关键字删除</h3>* 非递归实现** @param key 关键字* @return 被删除关键字对应值*/
public Object remove(int key) {BSTNode p = root;// 记录待删除节点的父亲BSTNode parent = null;while (p != null) {if (key < p.key) {parent = p;p = p.left;} else if (p.key < key) {parent = p;p = p.right;} else {break;}}if (p == null) {return null;}// 删除操作if (p.left == null) {shift(parent, p, p.right); // 情况1} else if (p.right == null) {shift(parent, p, p.left); // 情况2} else {// 情况4// 4.1 被删除节点找后继BSTNode s = p.right;BSTNode sParent = p; // 后继父亲while (s.left != null) {sParent = s;s = s.left;}// 4.2 删除和后继不相邻, 处理后继的后事if (sParent != p) { shift(sParent, s, s.right); // 不可能有左孩子(否则就不是后继节点)s.right = p.right;}// 4.3 后继取代被删除节点shift(parent, p, s);s.left = p.left;}return p.value;
}/*** 托孤方法** @param parent 被删除节点的父亲* @param deleted 被删除节点* @param child 被顶上去的节点*/
// 只考虑让 n1父亲的左或右孩子指向 n2, n1自己的左或右孩子并未在方法内改变
private void shift(BSTNode parent, BSTNode deleted, BSTNode child) {if (parent == null) {// 根节点(特殊情况)root = child;} else if (deleted == parent.left) {parent.left = child;} else {parent.right = child;}
}
测试代码:
public static void main(String[] args) {/*4/ \2 7/ \ /1 3 6/5*/BSTNode n1 = new BSTNode(1, 1);BSTNode n3 = new BSTNode(3, 3);BSTNode n2 = new BSTNode(2, 2, n1, n3);BSTNode n5 = new BSTNode(5, 5);BSTNode n6 = new BSTNode(6, 6, n5, null);BSTNode n7 = new BSTNode(7, 7, n6, null);BSTNode root1 = new BSTNode(4, 4, n2, n7);BSTTree tree1 = new BSTTree();tree1.root = root1;Object delete = tree1.remove(7);System.out.println(delete + "\t" + 7); // 7 7// 删除后/*4/ \2 6/ \ /1 3 5*/BSTNode x1 = new BSTNode(1, 1);BSTNode x3 = new BSTNode(3, 3);BSTNode x2 = new BSTNode(2, 2, x1, x3);BSTNode x5 = new BSTNode(5, 5);BSTNode x6 = new BSTNode(6, 6, x5, null);BSTNode root2 = new BSTNode(4, 4, x2, x6);BSTTree tree2 = new BSTTree();tree2.root = root2;System.out.println(isSameTree(tree1.root,tree2.root)); // true}// 判断是否为同一树(key对应的value都相等)static boolean isSameTree(BSTNode tree1, BSTNode tree2) {if (tree1 == null && tree2 == null) {return true;}if (tree1 == null || tree2 == null) {return false;}if (tree1.key != tree2.key) {return false;}return isSameTree(tree1.left, tree2.left) && isSameTree(tree1.right, tree2.right);}
测试结果如下,删除的元素符合预期,且删除后的树与预期结果的结构一致
7 7true
递归实现
由于递归实现效率低,且较难理解,主要是为了结合非递归实现提供思路,可以结合注释思考,不过多讲解,代码如下:
/*** <h3>根据关键字删除</h3>* 递归实现** @param key 关键字* @return 被删除关键字对应值*/public Object remove(int key) {ArrayList<Object> result = new ArrayList<>(); // 保存被删除节点的值root = doRemove(root, key, result);return result.isEmpty() ? null : result.get(0);}/*** 私有 递归删除具体实现细节** @param node 起点* @param key 删除索引* @param result 保存被删除节点的值* @return node 删剩下的孩子(找到) 或 null(没找到)* @author LiaoYuXing-Ray 2024/1/25 19:59**/private BSTNode doRemove(BSTNode node, int key, ArrayList<Object> result) {if (node == null) {return null;}if (key < node.key) {node.left = doRemove(node.left, key, result);return node;}if (node.key < key) {node.right = doRemove(node.right, key, result);return node;}result.add(node.value);if (node.left == null) { // 情况1 - 只有右孩子return node.right;}if (node.right == null) { // 情况2 - 只有左孩子return node.left;}BSTNode s = node.right; // 情况3 - 有两个孩子while (s.left != null) {s = s.left;}s.right = doRemove(node.right, s.key, new ArrayList<>());s.left = node.left;return s;}
说明
ArrayList<Object> result用来保存被删除节点的值- 第二、第三个 if 对应没找到的情况,继续递归查找和删除,注意后续的 doRemove返回值代表删剩下的,因此需要更新
- 最后一个 return 对应删除节点只有一个孩子的情况,返回那个不为空的孩子,待删节点自己因没有返回而被删除
- 第四个 if 对应删除节点有两个孩子的情况,此时需要找到后继节点,并在待删除节点的右子树中删掉后继节点,最后用后继节点替代掉待删除节点返回,别忘了改变后继节点的左右指针
3 二叉搜索树——范围查询
4/ \2 6/ \ / \1 3 5 7
3.1 找所有小于索引的值less(int key)
less(int key)方法:找 < key 的所有 value
使用中序遍历
// 找 < key 的所有 valuepublic List<Object> less(int key) {ArrayList<Object> result = new ArrayList<>();BSTNode p = root;LinkedList<BSTNode> stack = new LinkedList<>();while (p != null || !stack.isEmpty()) {if (p != null) {stack.push(p);p = p.left;} else {BSTNode pop = stack.pop();// 处理值if (pop.key < key) {result.add(pop.value);} else {break;}p = pop.right;}}return result;}3.2 找所有大于索引的值greater(int key)
greater(int key)方法:找 > key 的所有 value
使用常规的中序遍历(从左向右的中序遍历)
public List<Object> greater(int key) {ArrayList<Object> result = new ArrayList<>();BSTNode p = root;LinkedList<BSTNode> stack = new LinkedList<>();while (p != null || !stack.isEmpty()) {if (p != null) {stack.push(p);p = p.left;} else {BSTNode pop = stack.pop();if (pop.key > key) {result.add(pop.value);}p = pop.right;}}return result;
}
中序遍历效率不高,可以用 RNL 遍历(中序遍历的逆操作)
注:
- Pre-order, NLR
- In-order, LNR
- Post-order, LRN
- Reverse pre-order, NRL(反向前序遍历,值右左)
- Reverse in-order, RNL(反向中序遍历,右值左)
- Reverse post-order, RLN(反向后续序遍历,右左值)
RNL 遍历代码如下:
// 找 > key 的所有 value
public List<Object> greater(int key) {ArrayList<Object> result = new ArrayList<>();BSTNode p = root;LinkedList<BSTNode> stack = new LinkedList<>();while (p != null || !stack.isEmpty()) {if (p != null) {stack.push(p);p = p.right;} else {BSTNode pop = stack.pop();if (pop.key > key) {result.add(pop.value);} else {break;}p = pop.left;}}return result;
}
3.3 找范围值between(int key1, int key2)
between(int key1, int key2)方法:找 >= key1 且 <= key2 的所有值
// 找 >= key1 且 <= key2 的所有值public List<Object> between(int key1, int key2) {ArrayList<Object> result = new ArrayList<>();BSTNode p = root;LinkedList<BSTNode> stack = new LinkedList<>();while (p != null || !stack.isEmpty()) {if (p != null) {stack.push(p);p = p.left;} else {BSTNode pop = stack.pop();// 处理值if (pop.key >= key1 && pop.key <= key2) {result.add(pop.value);} else if (pop.key > key2) {break;}p = pop.right;}}return result;}
测试:
public static void main(String[] args) {/*4/ \2 6/ \ / \1 3 5 7*/BSTNode n1 = new BSTNode(1, 1);BSTNode n3 = new BSTNode(3, 3);BSTNode n2 = new BSTNode(2, 2, n1, n3);BSTNode n5 = new BSTNode(5, 5);BSTNode n7 = new BSTNode(7, 7);BSTNode n6 = new BSTNode(6, 6, n5, n7);BSTNode root = new BSTNode(4, 4, n2, n6);BSTTree tree = new BSTTree();tree.root = root;System.out.println(tree.less(6));System.out.println(tree.greater(6));System.out.println(tree.between(3,5));}
输出如下,符合预期
[1, 2, 3, 4, 5][7][3, 4, 5]
3.3 小结
优点:
- 如果每个节点的左子树和右子树的大小差距不超过一,可以保证搜索操作的时间复杂度是 O(log n),效率高。
- 插入、删除结点等操作也比较容易实现,效率也比较高。
- 对于有序数据的查询和处理,二叉查找树非常适用,可以使用中序遍历得到有序序列。
缺点:
- 如果输入的数据是有序或者近似有序的,就会出现极度不平衡的情况,可能导致搜索效率下降,时间复杂度退化成O(n)。
- 对于频繁地插入、删除操作,需要维护平衡二叉查找树,例如红黑树、AVL 树等,否则搜索效率也会下降。
- 对于存在大量重复数据的情况,需要做相应的处理,否则会导致树的深度增加,搜索效率下降。
- 对于结点过多的情况,由于树的空间开销较大,可能导致内存消耗过大,不适合对内存要求高的场景。
如果觉得这篇文章对您有所帮助的话,请动动小手点波关注💗,你的点赞👍收藏⭐️转发🔗评论📝都是对博主最好的支持~
相关文章:

瑞_数据结构与算法_二叉搜索树
文章目录 1 什么是二叉搜索树1.1 二叉搜索树的特征1.2 前驱后继 2 二叉搜索树的Java实现2.1 定义二叉搜索树节点类BSTNode泛型key改进 2.2 实现查找方法get(int key)递归实现非递归实现 ★非递归实现 泛型key版本 2.3 实现查找最小方法min()递归实现非递归实现 ★ 2.4 实现查找…...

Linux 命令行访问名字中包含空格的文件或文件夹
Linux 命令行访问名字中包含空格的文件或文件夹 References 在 Windows 下命名文件或文件夹名有空格是可以的,甚至在 Windows 和 Ubuntu 虚拟机共享的文件中也可以这么做,但是在 Ubuntu 中空格要用下划线代替,养成好习惯。Linux 会把空格当成…...

Dart/Flutter工具模块:the_utils
Flutter笔记 Dart/Flutter工具模块:the_utils 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/detail…...
矩阵号:日入100+,八大提示词(Prompt)使用技巧
最近在搞头条矩阵,发现自己的指令写的太烂了,一个指令将会决定你的写作质量。 收益比较拉垮,50个号收益好的,也就这么几个号。 于是我扒了一些提示词的操作技巧,分享一下自己的学习心得。 先说理论知识,实…...

爬虫工作量由小到大的思维转变---<第三十九章 Scrapy-redis 常用的那个RetryMiddleware>
前言: 为什么要讲这个RetryMiddleware呢?因为他很重要~ 至少在你装配代理ip或者一切关于重试的时候需要用到!----最关键的是:大部分的教学视频里面,没有提及这个!!!! 正文: 源代码分析 这个RetryMiddleware是来自: from scrapy.downloadermiddlewares.retry import Retry…...

【MongoDB】mongodb安装及启动踩坑点
mongodb的安装,基本上参考文章[1]。 但是在过程中,有一些踩坑点。 1,高版本mongodb不自带mongo脚本 在文章1中,作者在解压后,直接使用了mongo脚本,而我下载的mongodb版本要更高,在解压后&…...

动态规划——采矿的小奇【集训笔记】
题目描述 假期小奇去采矿场体验生活,工头为每个员工发放了一个最多能装 M 公斤的背包,经过一天的辛苦小奇开采出了 n 块矿石,它们的重量分别是W1,W2,...,Wn,经过预估它们的价值分别为C1,C2,...,Cn,那么请你…...
wpf控件Expander集合下的像素滚动
项目场景:Expander集合滚动 如下图,有一个Expander集合,且设置 ScrollViewer.VerticalScrollBarVisibility "Auto" 每个Expaner下包含有若干元素,当打开Expader(即IsExpanded "true")时&#…...

docker 基础手册
文章目录 docker 基础手册docker 容器技术镜像与容器容器与虚拟机docker 引擎docker 架构docker 底层技术docker 二进制安装docker 镜像加速docker 相关链接docker 生态 docker 基础手册 docker 容器技术 开源的容器项目,使用 Go 语言开发原意“码头工人”&#x…...
记一次SPI机制导致的BUG定位【不支持:http://javax.xml.XMLConstants/property/accessExternalDTD】
1、前因 今天在生产环境启用了某个功能,结果发现有个文件上传华为云OBS失败了,报错如下: Caused by: java.lang.IllegalArgumentException: 不支持:http://javax.xml.XMLConstants/property/accessExternalDTDat org.apache.xal…...
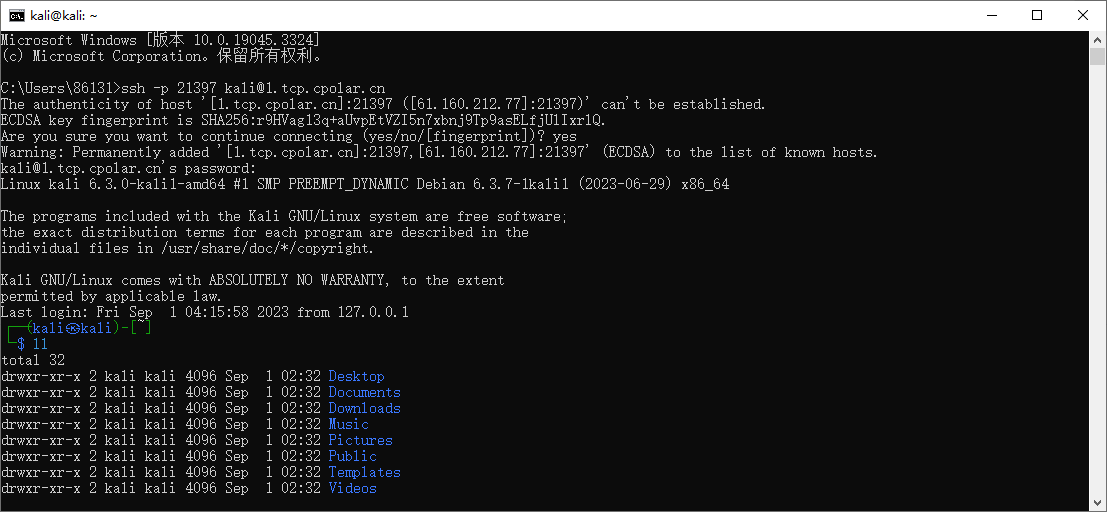
Kali如何启动SSH服务并实现无公网ip环境远程连接
文章目录 1. 启动kali ssh 服务2. kali 安装cpolar 内网穿透3. 配置kali ssh公网地址4. 远程连接5. 固定连接SSH公网地址6. SSH固定地址连接测试 简单几步通过[cpolar 内网穿透](cpolar官网-安全的内网穿透工具 | 无需公网ip | 远程访问 | 搭建网站)软件实现ssh 远程连接kali! …...
谷粒商城配置虚拟机
一、创建虚拟机 之前有在VM里面建一个ubuntu的虚拟机,准备拿来直接用,网络设置为NAT模式,查看我的虚拟机是虚拟机:192.168.248.128 主机: 192.168.2.12。可以互相ping通。 二、linux安装docker Docker docker是虚拟…...
Java中文乱码浅析及解决方案
Java中文乱码浅析及解决方案 一、GBK和UTF-8编码方式二、idea和eclipse的默认编码方式三、解码和编码方法四、代码实现编码解码 五、额外知识扩展 一、GBK和UTF-8编码方式 如果采用的是UTF-8的编码方式,那么1个英文字母 占 1个字节,1个中文占3个字节如果…...

【前端基础--3】
文字样式 1.文字颜色 color 取值方式: 英文单词 red green blue十六进制的颜色值 #000000 也可以写为#000(如aabbcc可以简写为abc)rgb三原色取值 color:rgb(220,32,215) 取值范围都在0~255之间 2.文字大小 font-size …...

Obsidian笔记软件结合cpolar实现安卓移动端远程本地群晖WebDAV数据同步
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

51单片机电子密码锁Proteus仿真+程序+视频+报告
目录 视频 设计分析 系统结构 仿真图 资料内容 资料下载地址:51单片机电子密码锁Proteus仿真程序视频报告 视频 单片机电子密码锁Proteus仿真程序视频 设计分析 (1)能够从键盘中输入密码,并相应地在显示器上显示‘*’; (2)能够判断密码…...
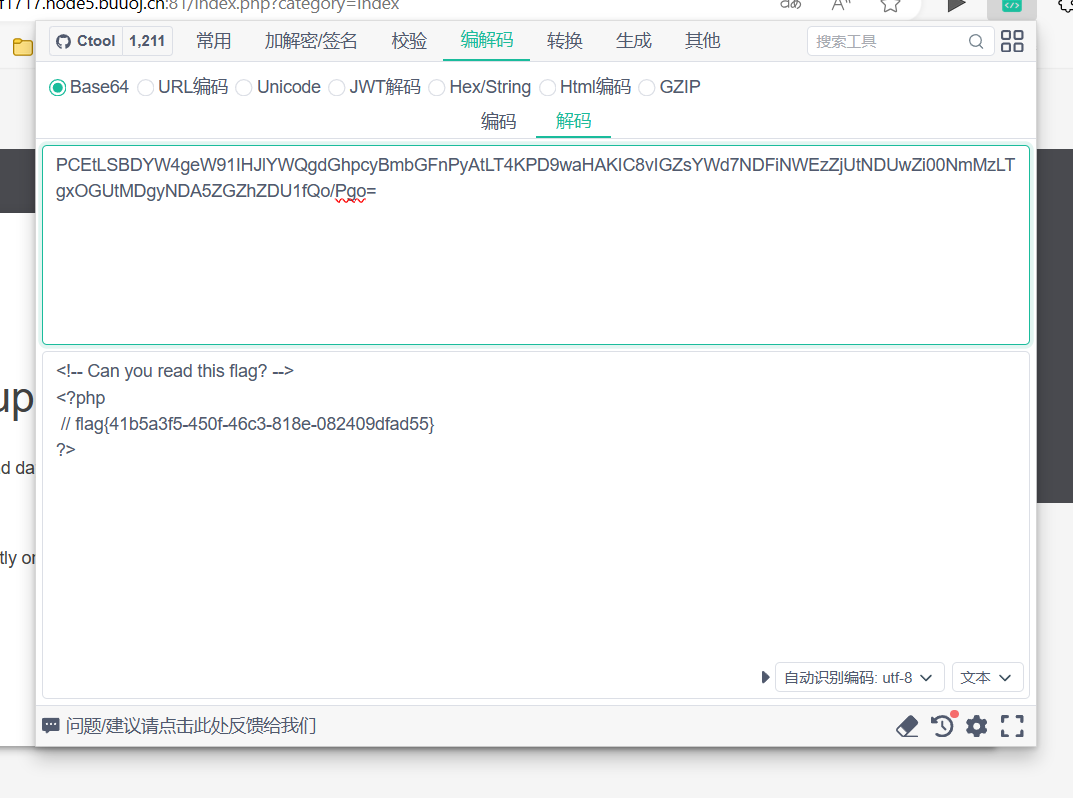
[BSidesCF 2020]Had a bad day
先看url,发现可能有注入 http://655c742e-b427-485c-9e15-20a1e7ef1717.node5.buuoj.cn:81/index.php?categorywoofers 试试能不能查看index.php直接?categoryindex.php不行,试试伪协议 把.php去掉试试 base64解码 <?php$file $_GET[category];…...

[笔记]事务简介-springboot
在Spring Boot中,事务的管理通常通过注解来实现,使得配置变得简单而直观。这种方式与Spring Boot的设计理念一致,即减少显式配置,增加自动配置。以下是如何在Spring Boot项目中应用和管理事务的详细说明: Spring Boot中…...
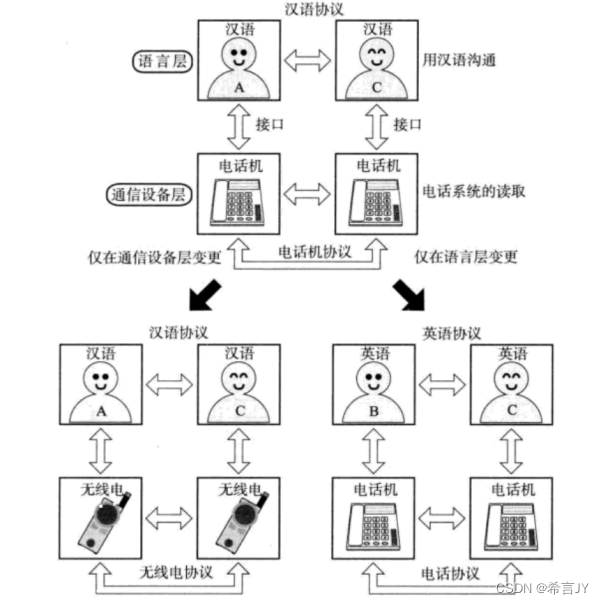
初识计算机网络 | 计算机网络的发展 | 协议初识
1.计算机网络的发展 “矛盾是普遍存在的,矛盾是事物联系的实质内容和事物发展的根本动力!” 计算机在诞生之初,在军事上用来计算导弹的弹道轨迹!在发展的过程中(商业的推动,国家政策推动)&…...
【sgTree】自定义组件:加载el-tree树节点整棵树数据,实现增删改操作。
特性 可以自定义主键、配置选项支持预定义节点图标:folder文件夹|normal普通样式多个提示文本可以自定义支持动态接口增删改节点可以自定义根节点id可以设置最多允许添加的层级深度支持拖拽排序,排序过程还可以针对拖拽的节点深度进行自定义限制支持隐藏…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
