选择排序(堆排序和topK问题)
选择排序
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
如果我们用扑克牌来举例,那么选择排序就像是提前已经把所有牌都摸完了,而再进行牌之间的排序;而插入排序则是边摸边排。
直接选择排序
- 在元素集合array[i]–array[n-1]中选择关键码最大(小)的数据元素
- 若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换
- 在剩余的array[i]–array[n-2](array[i+1]–array[n-1])集合中,重复上述步骤,直到集合剩余1个元素
直接选择排序的特性总结:
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
那么下面我先将代码展示给大家,然后再为大家讲解其中奥妙
void SelectSort(int* a, int n) {int begin = 0;int end = n - 1;while (begin < end) {int min = begin;int max = begin;for (int i = begin + 1; i <= end; i++) {if (a[i] < min) {min = i;}if (a[i] > max) {max = i;}}Swap(&a[begin], &a[min]);if (max == begin){max = min;}Swap(&a[end], &a[max]);begin++;end--;}
}
首先呢,我们先把起始位置的下标和最后位置的下标给记录下来,并将最小值和最大值的下标都初始化为begin,外面再套上一层循环,限制条件为begin<end,当两个下标走到一起或者错开时,就会结束循环,也就排好了。
而while循环里面的才是排序的逻辑部分,for循环从begin的下一个位置开始,到end的位置结束,并在其中进行比较,改变每一次循环中最大值和最小值的下标,并在循环结束后交换最小值和begin下标值的位置,最大值与end下标值的位置,最后begin和end都往中间走,开始下一轮循环
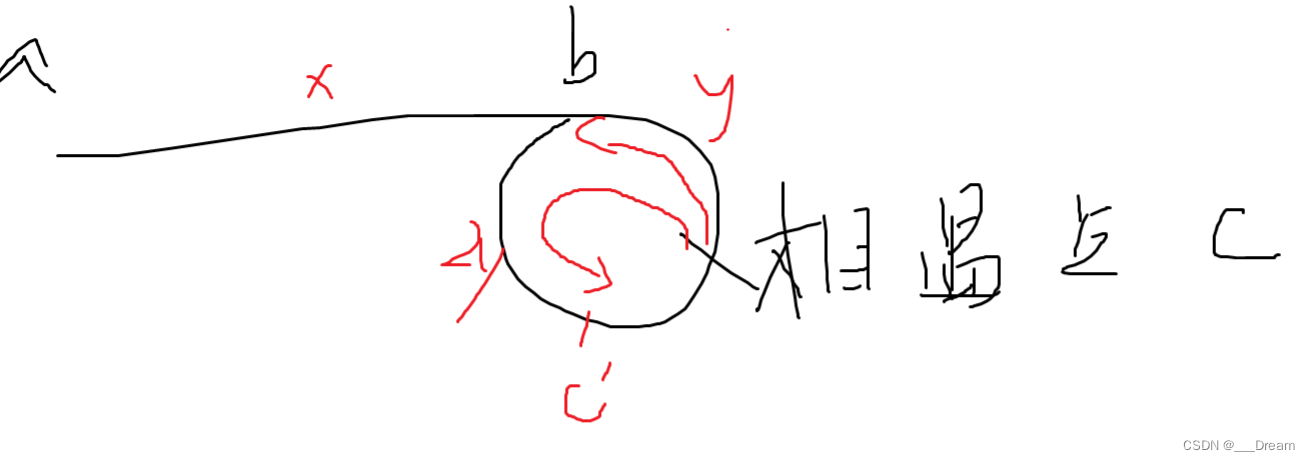
不过需要注意的是,我们加入了一个if判断语句:其实这是为了防止最大值就在begin下标时,原来的最大值会和最小值交换位置,然后最小值会被换到end的位置上成为最大值,那样子的话就会出现错误,排序便失败了;但加上这个之后,在第一次交换过后,max的值到了min的下标,这个时候只需要把max下标也改为min,这个时候替换就不会再把最小值给替换到最后,而是最大值了。这样讲可能也有点绕,给大家画个图便于理解。
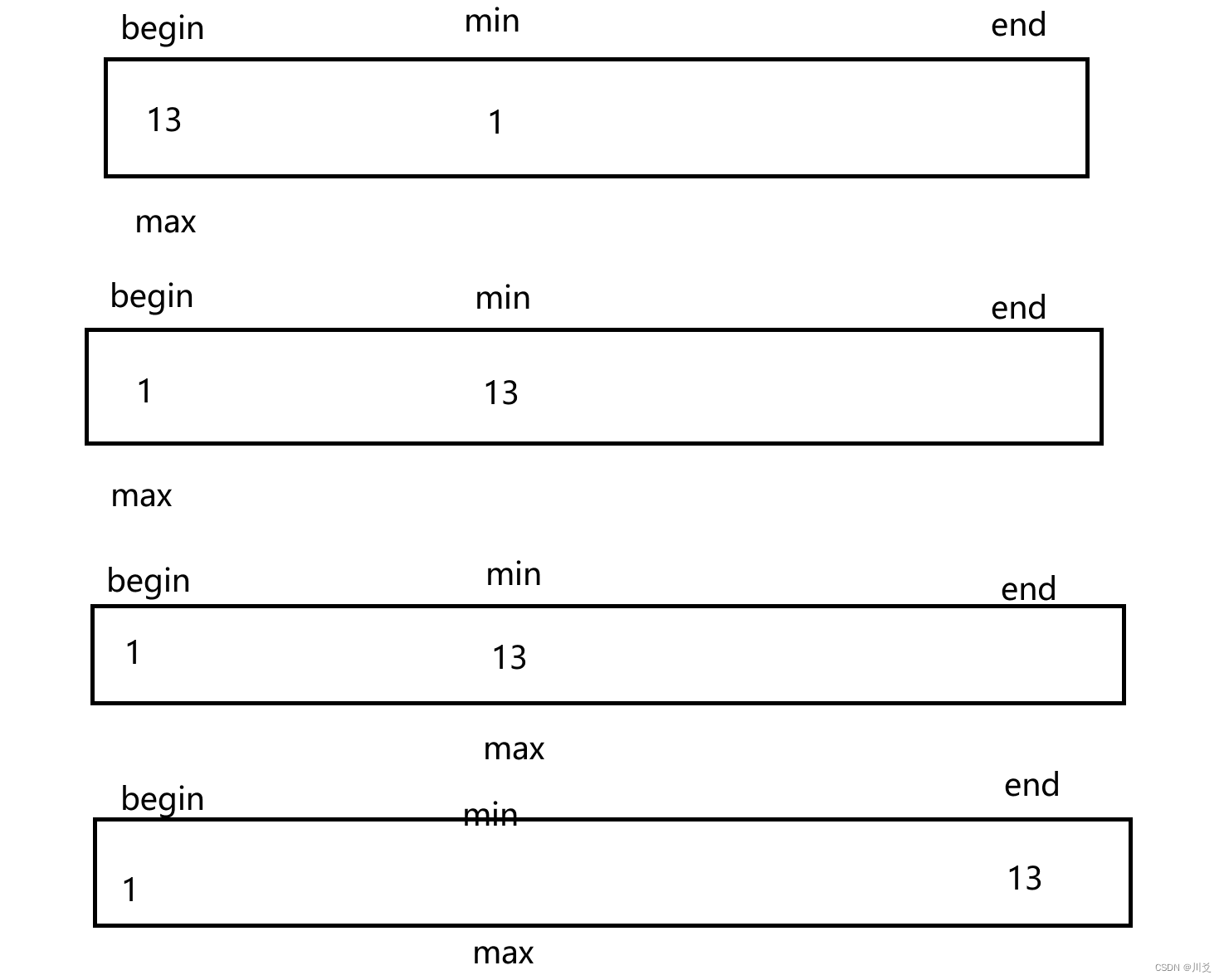
相信大家根据函数看就可以看懂啦!还是很好理解的!
堆排序
相比于刚才的直接选择排序,想必当然还是堆排序更加吸引大家的注意,那就让我们开始学习吧!
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
堆排序的特性总结:
- 堆排序使用堆来选数,效率就高了很多。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
代码如下~
void HeapSort(int* a, int n) {for (int i = 0; i < n; i++) {AdjustUp(a, i);//建大堆}int end = n - 1;while (end > 0) {Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}
虽然堆排序的本体很小,但是千万不能忽视了向上调整算法和向下调整算法,所以还是把这一串代码附在下面
void AdjustUp(int* a, int child) {int parent = (child - 1) / 2;while (child > 0) {if (a[child] > a[parent]) {Swap(&a[child], &a[parent]);}else {break;//这里没必要return}child = parent;parent = (parent - 1) / 2;}
}void AdjustDown(int* a, int size, int parent) {int child = parent * 2 + 1;//假设左子节点小于右子节点//右子节点不一定有,可能会越界while (child < size) {if (child + 1 < size && a[child + 1] > a[child]) {child++;//其实就是左子节点转换到右子节点上}if (a[child] > a[parent]) {Swap(&a[child], &a[parent]);parent = child;//parent移动到原来child的位置上child = child * 2 + 1;//child来寻找自己的下一个左子节点}else {break;}}
}
虽然堆排序中有堆,但是我们不可能真的建一个堆然后再进行排序,毕竟手搓一个堆的函数还是挺麻烦的,所以我们本质上是模拟堆插入的过程建堆,并利用其逻辑对数组中的元素进行排序,我们还是用例子说话。并且在建堆之前还有一个需要注意的,因为现在给的例子是以升序排列,所以我们现在建立的是大堆(需要在向上调整算法和向下调整算法中改变大于小于符号)
建立大堆的原因还有一个,那就是如果建立小堆的话,当删除堆顶元素(最小值)时,剩下的数还看作堆的话,关系就全乱了,需要重新建堆,浪费时间。
第一步:建堆
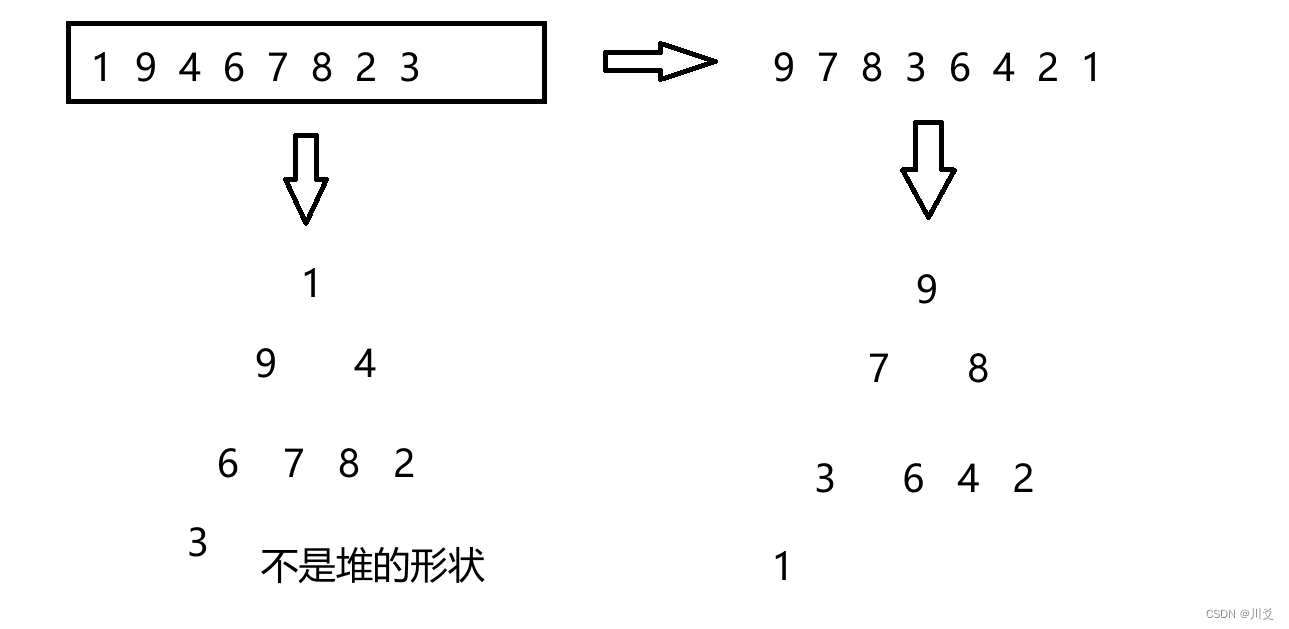
第二步:排序
其实就是将end定为数组的最后一个下标n-1,然后堆顶元素和最后一个元素交换,向下调整之后,删除最后一个元素,最后end走到0下标的时候就结束,写一两步大家看看
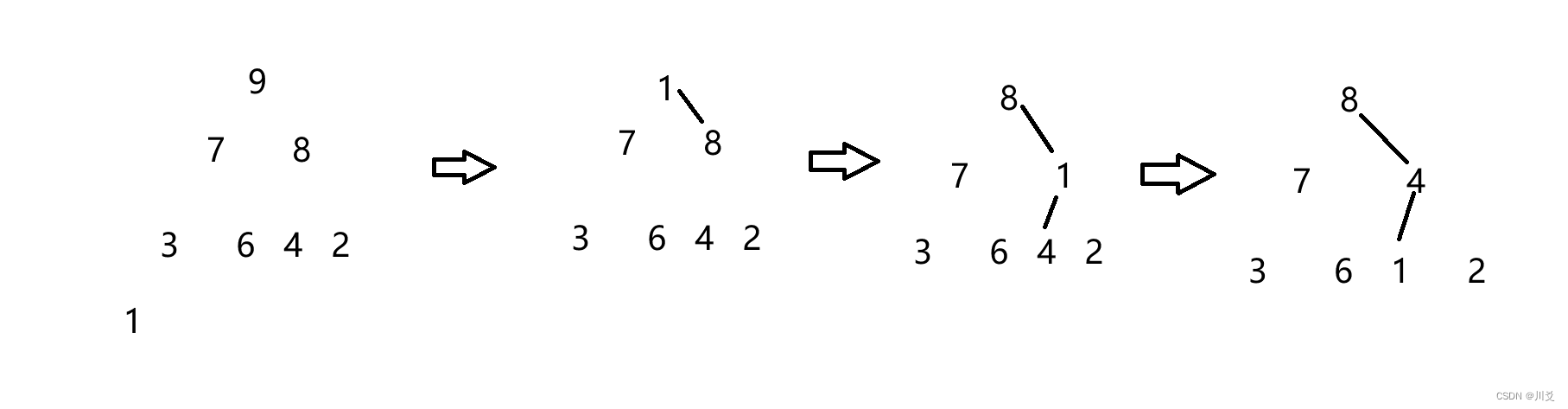
实际上,虽然在堆中删除了,但我们直到此时9已经到了n-1下标的位置,也就是排在了最大值的位置上。而向下调整之后,我们会发现,8又到了最上方,并且也是目前的最大值,也就是下一次,8会与2交换,成为次大的值;2又与7交换,2又与6交换,那么很明显,下一次循环交换的数就是7了,之后就是6,这样,最大值就慢慢的被调节到了end的位置,最后数组中的元素都正序排列。
优化
除了使用向上调整建堆,其实我们还可以使用向下调整建堆,进行讲解后,大家甚至还会发现向下调整更加简洁方便
for (int i = (n-1-1)/2; i >= 0; --i){AdjustDown(a, n, i);}
以上便是将向上调整改为向下调整算法后的函数,为什么从(n-1-1)/2开始呢,是因为n-1是最后一个元素的下标,而(n-1-1)/2则是找到其父节点,然后从底端进行调整。
而至于为什么向下建堆更简洁呢?给大家用数学写写,大家就懂啦!
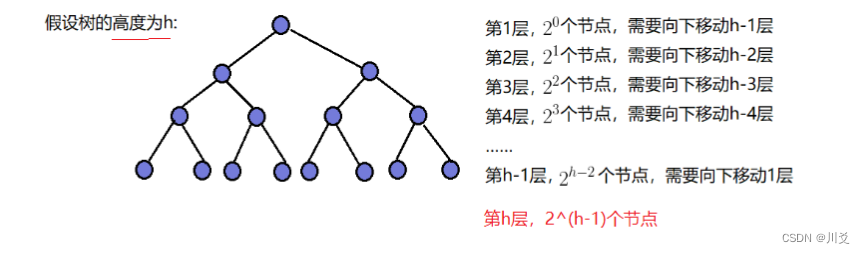
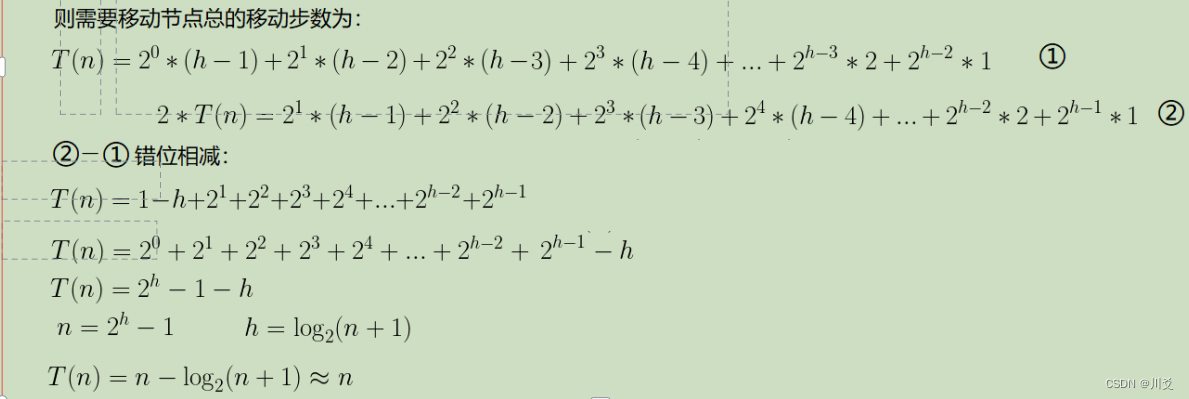
eg.n=2^h-1上面的T(n)都是T(h),到下面才是T(n),写错了QAQ
由此可以看出,向下调整建堆的时间复杂度为O(n),下面我们计算向上调整建堆的时间复杂度

由此可知:向上调整建堆的时间复杂度为O(nlogn),是大于向下调整建堆的,这样子的话,我们以后如果使用堆排序,我们就可以直接忽略向上调整算法,只写向下调整算法,代码量可以更少,时间复杂度也更精简
topK问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
- 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆- 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
void PrintTopK(int* a, int n, int k) {int* heap = (int*)malloc(sizeof(int) * k);if (heap == NULL) {perror("malloc fail");return;}for (int i = 0; i < k; ++i) {heap[i] = a[i];AdjustUp(heap, i);//先用前k个数创建一个小堆}for (int i = k; i < n; ++i) {if (a[i] > heap[0]) {heap[0] = a[i];//从k下标开始遍历数据,如果大于heap[0],就让其成为heap[0]AdjustDown(heap, k, 0);//然后向下调整}}for (int i = 0; i < k; ++i) {printf("%d ", heap[i]);//打印最大的k个数}printf("\n");free(heap);//记住释放heap开辟的内存
}
我们还是照样举一个例子,虽然topK是在n大于k很多的情况下才使用的,但为了看上去简单,我们选择两个相近的n与k
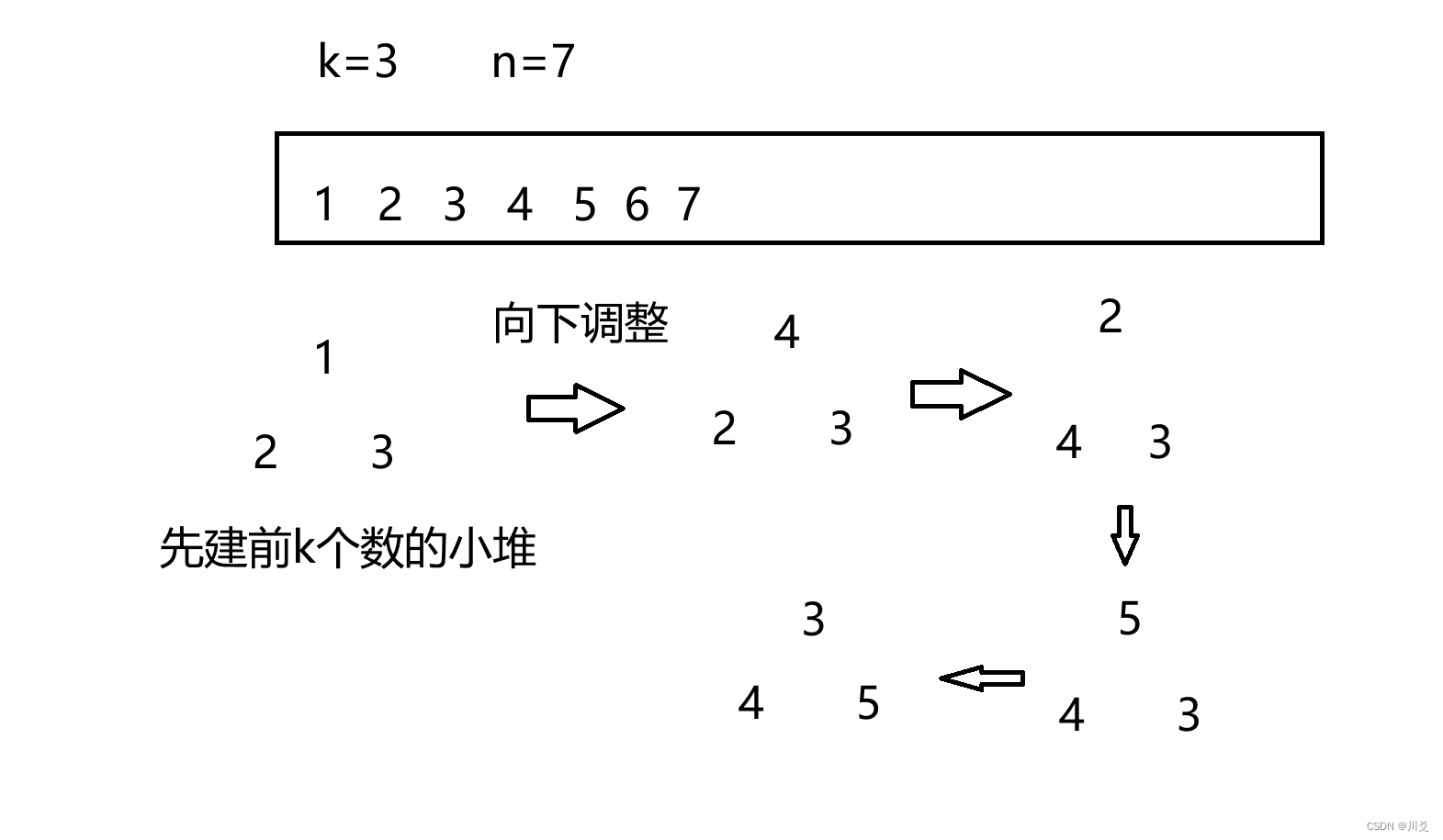
我们在插入后进行了两次向下调整,由此可知,当我们进行完所有的向下调整之后,留在k个元素小堆中的元素一定是最大的几个
当然,除了从数组中取出的方法,我们还可以写出一种从文件中拿出数据并排序的topK函数,大家请看!
void CreateNDate()
{// 造数据int n = 10000000; // 设置要生成的数据数量srand(time(0)); // 使用当前时间作为随机数种子,确保每次运行生成的随机数不同const char* file = "data.txt"; // 指定数据文件的名称FILE* fin = fopen(file, "w"); // 以写模式打开文件if (fin == NULL){perror("fopen error"); // 输出文件打开错误信息return;}// 随机生成n个整数,并将其写入文件for (int i = 0; i < n; ++i){int x = (rand() + i) % 10000000; // 生成0到9999999之间的随机整数,加i是因为随机数最多只可以生成3万多个,会有重复的,这样能保证重复率大大降低fprintf(fin, "%d\n", x); // 将随机数写入文件}fclose(fin); // 关闭文件
}
void PrintTopK(const char* file, int k)
{FILE* fout = fopen(file, "r"); // 以只读模式打开文件if (fout == NULL){perror("fopen error"); // 输出文件打开错误信息return;}// 建一个k个数小堆int* minheap = (int*)malloc(sizeof(int) * k); // 分配大小为k的整型数组内存if (minheap == NULL){perror("malloc error"); // 输出内存分配错误信息return;}// 读取前k个数,构建最小堆for (int i = 0; i < k; i++){fscanf(fout, "%d", &minheap[i]); // 从文件中读取整数,构建最小堆AdjustUp(minheap, i); // 执行向上调整,维护最小堆性质}int x = 0;while (fscanf(fout, "%d", &x) != EOF) // 从文件中读取整数,直到文件结束{if (x > minheap[0]) // 如果当前数字大于堆顶元素{minheap[0] = x; // 将堆顶元素替换为当前数AdjustDown(minheap, k, 0); // 执行向下调整,维护最小堆性质}}for (int i = 0; i < k; i++){printf("%d ", minheap[i]); // 输出最小堆中的前k个元素}printf("\n");free(minheap); // 释放动态分配的堆内存fclose(fout); // 关闭文件
}
以上就是选择排序中的几个问题,下一节排序,我们讲解的是交换排序,欢迎大家持续收看!
相关文章:

选择排序(堆排序和topK问题)
选择排序 每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。 如果我们用扑克牌来举例,那么选择排序就像是提前已经把所有牌都摸完了,而再进行牌…...

webpack tree shaking 摇树原理
Tree-shaking 是指在打包过程中通过静态分析,识别并删除未使用的代码,以减小最终输出文件的大小。Webpack 通过内置的 UglifyJS 插件或者 Terser 插件来实现 Tree-shaking。下面是简要的 webpack Tree-shaking 的原理: 标记未使用的代码&…...
)
开源模型应用落地-业务整合篇(三)
一、前言 在之前的两篇文章中,我们学习了如何构建基本的即时消息(IM)功能。今天,我们将进一步将IM模块与AI服务进行连接,实现用户提问并由模型进行回答,最后将结果展示在用户界面上。 二、术语 2.1. Spring Boot 是一个用于快速构建基于Spring框架的Java应用程序的开源框…...

js打地鼠
文章目录 1实现效果2代码实现 1实现效果 游戏难度:简单,一般,困难,噩梦(控制setInterval的time参数) 按钮功能:结束(可以通过修改gameScore的值来修改判定结束的分数)&am…...

计算机网络体系架构认知--网络协议栈
文章目录 一.计算机网络分层架构各协议层和计算机系统的联系从整体上理解计算机网络通信计算机网络通信的本质 二.Mac地址,IP地址和进程端口号三.局域网通信与跨局域网通信局域网通信跨局域网通信全球互联的通信脉络 四.网络编程概述 一.计算机网络分层架构 实现计算机长距离网…...

Ubuntu 22.04 安装tomcat
tomcat是常用的Java服务容器,这篇文章我们就来讲讲如何安装它。 更新软件包 首先是更新软件包,这是最常规的操作 sudo apt update 然后是开始安装,不多一会就可以安装好了 sudo apt install tomcat9 然后看一下状态 sudo systemctl status tomcat9 发现虽然启动了,但…...

记录:Ubuntu 18.04 X86 上通过CMake 指定编译器工具链交叉编译。
最好是通过 cmake 命令行来设置,要不然你只有在 CMakeFiles.txt 里面自己写判断语句了。 要用 cmake 交叉编译,必须设置连接器,要不然会使用当前系统的 ld,就是 /usr/bin/ld。 但是其它平台是不会ld上的,elf格式都不…...
requests,js逆向练习
自上而下排除jquery源码,点进去utils 发现第一次请求是getTime 再次运行此断点才是登录,这个时候密码已经被加密了 查看上级js页面,发现加密函数 进去看函数加密过程 得到结果RSA python代码 import base64 import jsonimport requests f…...
Chrome 插件调试
http://blog.haoji.me/chrome-plugin-develop.html#te-bie-zhu-yi-background-de-bao-cuo 手把手:Chrome浏览器开发系列(四):调试我们开发的插件 - 掘金...

云轴科技ZStack成为交通运输业上云用云推进中心首批成员单位
近日,中国信息通信研究院、中国交通运输协会信息专业委员会联合发起成立“交通运输业上云用云推进中心”,上海云轴信息科技有限公司(简称云轴科技ZStack)凭借优秀的产品技术创新能力和在交通运输领域的实践经验成为首批成员单位并…...
代码随想录算法训练营31期day4,力扣24+19+02.07+142
24,动指针 class Solution { public:ListNode* swapPairs(ListNode* head) {//建立虚拟头结点auto dummynew ListNode(-1);dummy->nexthead;for(auto pdummy;p->next&&p->next->next;){auto ap->next;auto ba->next;p->nextb;a->n…...

eNSP学习——利用单臂路由实现VLAN间路由
目录 原理概述 实验内容 实验目的 实验步骤 实验拓扑 实验编址 配置步骤 创建VLAN并配置Access、Trunk接口 配置路由器子接口和IP地址 配置路由器子接口封装VLAN 测试结果 原理概述 在以太网中,通常会使用VLAN技术隔离二层广播域来减少广播的影响&#…...

ISO27001认证:企业与个人发展的必备之选
ISO27001认证,对于企业和个人来说,都具有极高的价值和重要性。作为国际权威的信息安全管理体系标准,它为企业提供了保障信息安全、防范风险和提升竞争力的有力工具。 💼对企业的价值: ISO27001认证可以帮助企业满足国家…...
SpringBoot使用druid
SpringBoot使用druid 一、前言二、配置1、pom依赖2、配置文件yml3、配置类 一、前言 Java程序很大一部分要操作数据库,为了提高性能操作数据库的时候,又不得不使用数据库连接池。 Druid 是阿里巴巴开源平台上一个数据库连接池实现,结合了 C…...

TongWeb8交流常见问答集
问题1:今后用到你们TongWeb产品该联系谁? 答复: 1. 商务问题,如:报价、license授权、合同等请联系销售。 2. TongWeb技术问题,未签项目联系售前,已签项目联系售后。有指定项目经理的项目&…...

GBASE南大通用分享-mysql中的load data infile用法
GBASE南大通用分享 mysql中的load data infile用法 LOAD DATA [LOW_PRIORITY] [LOCAL] INFILE file_name.txt [REPLACE | IGNORE] INTO TABLE tbl_name [FIELDS [TERMINATED BY \t] [OPTIONALLY] ENCLOSED BY ] [ESCAPED BY \\ ]] [LINES TERMINATED BY \n] [IGNORE number L…...
Ubuntu18编译jdk8源码
环境 系统 ubuntu18 Linux ubuntu 5.4.0-150-generic #167~18.04.1-Ubuntu SMP Wed May 24 00:51:42 UTC 2023 x86_64 x86_64 x86_64 GNU/Linux jdk源码openjdk-8u41-src-b04-14_jan_2020.zip bootJdk jdk-8u391-linux-x64.tar.gz ps -e|grep ssh sudo apt-get install ssh…...

《开始使用PyQT》 第01章 PyQT入门 02 安装Python3和PyQT6
02 安装Python3和PyQT6 《开始使用PyQT》 第01章 PyQT入门 02 安装Python3和PyQT6 So that all readers are on the same page, let’s begin by installing or updating your version of Python. 为了让所有读者都能理解,让我们从安装或更新 Python 版本开始。 …...
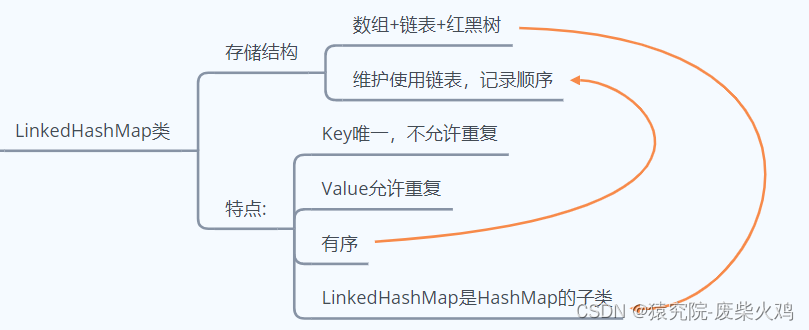
Java集合-Map接口(key-value)
Map接口的特点:①KV键值对方式存储②Key键唯一,Value允许重复③无序。 Map有四个实现类:1.HashMap类2.LinkedHashMap类3.TreeMap类4.Hashtable类 1.HashMap类: 存储结构:哈希表 数组Node[ ] 链表(红黑…...

【操作系统】实验九 写一个设备驱动程序
🕺作者: 主页 我的专栏C语言从0到1探秘C数据结构从0到1探秘Linux 😘欢迎关注:👍点赞🙌收藏✍️留言 🏇码字不易,你的👍点赞🙌收藏❤️关注对我真的很重要&…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
