《动手学深度学习(PyTorch版)》笔记4.4
注:书中对代码的讲解并不详细,本文对很多细节做了详细注释。另外,书上的源代码是在Jupyter Notebook上运行的,较为分散,本文将代码集中起来,并加以完善,全部用vscode在python 3.9.18下测试通过。
Chapter4 Multilayer Perceptron
4.4 Model Selection
作为机器学习科学家,我们的目标是发现模式(pattern)。但是,我们如何才能确定模型是真正发现了一种泛化的模式,而不是简单地记住了数据呢?例如,我们想要在患者的基因数据与痴呆状态之间寻找模式,其中标签是从集合 { 痴呆 , 轻度认知障碍 , 健康 } \{\text{痴呆}, \text{轻度认知障碍}, \text{健康}\} {痴呆,轻度认知障碍,健康}中提取的,因为基因可以唯一确定每个个体(不考虑双胞胎),所以在这个任务中是有可能记住整个数据集的。我们不想让模型只会做这样的事情:“那是鲍勃!我记得他!他有痴呆症!”。原因很简单:当我们将来部署该模型时,模型需要判断从未见过的患者。只有当模型真正发现了一种泛化模式时,才会作出有效的预测。
更正式地说,我们的目标是发现某些模式,这些模式捕捉到了我们训练集潜在总体的规律。如果成功做到了这点,即使是对以前从未遇到过的个体,模型也可以成功地评估风险。如何发现可以泛化的模式是机器学习的根本问题。
困难在于,当我们训练模型时,我们只能访问数据中的小部分样本。最大的公开图像数据集包含大约一百万张图像。而在大部分时候,我们只能从数千或数万个数据样本中学习。在大型医院系统中,我们可能会访问数十万份医疗记录。当我们使用有限的样本时,可能会遇到这样的问题:当收集到更多的数据时,会发现之前找到的明显关系并不成立。
将模型在训练数据上拟合的比在潜在分布中更接近的现象称为过拟合(overfitting),用于对抗过拟合的技术称为正则化(regularization)。在前面的章节中,有些读者可能在用Fashion-MNIST数据集做实验时已经观察到了这种过拟合现象。在实验中调整模型架构或超参数时会发现:如果有足够多的神经元、层数和训练迭代周期,模型最终可以在训练集上达到完美的精度,此时测试集的准确性却下降了。
4.4.1 Training Error and Generalization Error
训练误差(training error)指模型在训练数据集上计算得到的误差。泛化误差(generalization error)指模型应用在同样从原始样本的分布中抽取的无限多数据样本时,模型误差的期望。问题是,我们永远不能准确地计算出泛化误差。这是因为无限多的数据样本是一个虚构的对象。在实际中,我们只能通过将模型应用于一个独立的测试集来估计泛化误差,该测试集由随机选取的、未曾在训练集中出现的数据样本构成。
考虑一个简单地使用查表法来回答问题的模型。如果允许的输入集合是离散的并且相当小,那么也许在查看许多训练样本后,该方法将执行得很好。但当这个模型面对从未见过的例子时,它表现的可能比随机猜测好不到哪去。这是因为输入空间太大了,远远不可能记住每一个可能的输入所对应的答案。例如,考虑 28 × 28 28\times28 28×28的灰度图像。如果每个像素可以取 256 256 256个灰度值中的一个,则有 25 6 784 256^{784} 256784个可能的图像。这意味着指甲大小的低分辨率灰度图像的数量比宇宙中的原子要多得多。即使我们可能遇到这样的数据,我们也不可能存储整个查找表。
最后,考虑对掷硬币的结果(类别0:正面,类别1:反面)进行分类的问题。假设硬币是公平的,无论我们想出什么算法,泛化误差始终是 1 2 \frac{1}{2} 21。然而,对于大多数算法,我们应该期望训练误差会更低(取决于运气)。考虑数据集{0,1,1,1,0,1}。我们的算法不需要额外的特征,将倾向于总是预测多数类,从我们有限的样本来看,它似乎是1占主流。在这种情况下,总是预测类1的模型将产生 1 3 \frac{1}{3} 31的误差,这比我们的泛化误差要好得多。当我们逐渐增加数据量,正面比例明显偏离 1 2 \frac{1}{2} 21的可能性将会降低,我们的训练误差将与泛化误差相匹配。
4.4.1.1 I.I.D. Assumption
在我们目前已探讨、并将在之后继续探讨的监督学习情景中,我们假设训练数据和测试数据都是从相同的分布中独立提取的。这通常被称为独立同分布假设(i.i.d. assumption),这意味着对数据进行采样的过程没有进行“记忆”。换句话说,抽取的第2个样本和第3个样本的相关性,并不比抽取的第2个样本和第200万个样本的相关性更强。
要成为一名优秀的机器学习科学家需要具备批判性思考能力。假设是存在漏洞的,即很容易找出假设失效的情况。如果我们根据从加州大学旧金山分校医学中心的患者数据训练死亡风险预测模型,并将其应用于马萨诸塞州综合医院的患者数据,结果会怎么样?这两个数据的分布可能不完全一样。此外,抽样过程可能与时间有关。比如当我们对微博的主题进行分类时,新闻周期会使得正在讨论的话题产生时间依赖性,从而违反独立性假设。
有时候我们即使轻微违背独立同分布假设,模型仍将继续运行得非常好。比如,我们有许多有用的工具已经应用于现实,如人脸识别、语音识别和语言翻译。毕竟,几乎所有现实的应用都至少涉及到一些违背独立同分布假设的情况。
有些违背独立同分布假设的行为肯定会带来麻烦。比如,我们试图只用来自大学生的人脸数据来训练一个人脸识别系统,然后想要用它来监测疗养院中的老人。这不太可能有效,因为大学生看起来往往与老年人有很大的不同。
在接下来的章节中,我们将讨论因违背独立同分布假设而引起的问题。目前,即使认为独立同分布假设是理所当然的,理解泛化性也是一个困难的问题。此外,能够解释深层神经网络泛化性能的理论基础,也仍在继续困扰着学习理论领域的学者们。当我们训练模型时,我们试图找到一个能够尽可能拟合训练数据的函数。但是如果它执行地“太好了”,而不能对看不见的数据做到很好泛化,就会导致过拟合。这种情况正是我们想要避免或控制的,深度学习中有许多启发式的技术旨在防止过拟合。
4.4.1.2 Model Complexity
当我们有简单的模型和大量的数据时,我们期望泛化误差与训练误差相近。当我们有更复杂的模型和更少的样本时,我们预计训练误差会下降,但泛化误差会增大。模型复杂性由什么构成是一个复杂的问题。一个模型是否能很好地泛化取决于很多因素。例如,具有更多参数的模型可能被认为更复杂,参数有更大取值范围的模型可能更为复杂。通常对于神经网络,我们认为需要更多训练迭代的模型比较复杂,而需要早停(early stopping)的模型(即较少训练迭代周期)就不那么复杂。
本节为了给出一些直观的印象,我们将重点介绍几个倾向于影响模型泛化的因素。
- 可调整参数的数量。当可调整参数的数量(有时称为自由度)很大时,模型往往更容易过拟合。
- 参数采用的值。当权重的取值范围较大时,模型可能更容易过拟合。
- 训练样本的数量。即使模型很简单,也很容易过拟合只包含一两个样本的数据集。而过拟合一个有数百万个样本的数据集则需要一个极其灵活的模型。
4.4.2 Model Selection
在机器学习中,我们通常在评估几个候选模型后选择最终的模型,这个过程叫做模型选择。我们有时需要进行比较的模型在本质上是完全不同的(如决策树与线性模型),有时又需要比较不同的超参数设置下的同一类模型。
4.4.2.1 Validation Dataset
训练多层感知机模型时,我们可能希望比较具有不同数量的隐藏层、不同数量的隐藏单元以及不同的激活函数组合的模型。为了确定候选模型中的最佳模型,我们通常会使用验证集。原则上,在我们确定所有的超参数之前,我们不希望用到测试集。如果我们在模型选择过程中使用测试数据,可能会有过拟合测试数据的风险,那就麻烦大了。如果我们过拟合了训练数据,还可以在测试数据上的评估来判断过拟合。但是如果我们过拟合了测试数据,我们又该怎么知道呢?
因此,我们决不能依靠测试数据进行模型选择。然而,我们也不能仅仅依靠训练数据来选择模型,因为我们无法估计训练数据的泛化误差。在实际应用中,情况变得更加复杂。虽然理想情况下我们只会使用测试数据一次,以评估最好的模型或比较一些模型效果,但现实是测试数据很少在使用一次后被丢弃。我们很少能有充足的数据来对每一轮实验采用全新测试集。
解决此问题的常见做法是将我们的数据分成三份,除了训练和测试数据集之外,还增加一个验证数据集(validation dataset),也叫验证集(validation set)。但现实是验证数据和测试数据之间的边界模糊得令人担忧。除非另有明确说明,否则在这本书的实验中,我们实际上是在使用应该被正确地称为训练数据和验证数据的数据集,并没有真正的测试数据集。因此,书中每次实验报告的准确度都是验证集准确度,而不是测试集准确度。
4.4.2.2 K-Fold Cross Validation
当训练数据稀缺时,我们甚至可能无法提供足够的数据来构成一个合适的验证集。这个问题的一个流行的解决方案是采用 K K K折交叉验证。这里,原始训练数据被分成 K K K个不重叠的子集。然后执行 K K K次模型训练和验证,每次在 K − 1 K-1 K−1个子集上进行训练,并在剩余的一个子集(在该轮中没有用于训练的子集)上进行验证。最后,通过对 K K K次实验的结果取平均来估计训练和验证误差。
4.4.3 Underfitting and Overfitting
当我们比较训练和验证误差时,我们要注意两种常见的情况。首先,我们要注意这样的情况:训练误差和验证误差都很严重,但它们之间仅有一点差距。如果模型不能降低训练误差,这可能意味着模型过于简单(即表达能力不足),无法捕获试图学习的模式。此外,由于我们的训练和验证误差之间的泛化误差很小,我们有理由相信可以用一个更复杂的模型降低训练误差。这种现象被称为欠拟合(underfitting)。
另一方面,当我们的训练误差明显低于验证误差时要小心,这表明严重的过拟合(overfitting)。注意,过拟合并不总是一件坏事。特别是在深度学习领域,众所周知,最好的预测模型在训练数据上的表现往往比在保留(验证)数据上好得多。最终,我们通常更关心验证误差,而不是训练误差和验证误差之间的差距。
是否过拟合或欠拟合可能取决于模型复杂性和可用训练数据集的大小,这两点将在下面进行讨论。
4.4.3.1 Model Complexity
为了说明一些关于过拟合和模型复杂性的经典直觉,我们给出一个多项式的例子。给定由单个特征 x x x和对应实数标签 y y y组成的训练数据,我们试图找到下面的 d d d阶多项式来估计标签 y y y。
y ^ = ∑ i = 0 d x i w i \hat{y}= \sum_{i=0}^d x^i w_i y^=i=0∑dxiwi
这只是一个线性回归问题,我们的特征是 x x x的幂给出的,模型的权重是 w i w_i wi给出的,偏置是 w 0 w_0 w0给出的(因为对于所有的 x x x都有 x 0 = 1 x^0 = 1 x0=1)。由于这只是一个线性回归问题,我们可以使用平方误差作为我们的损失函数。
高阶多项式的参数较多,模型函数的选择范围较广。因此在固定训练数据集的情况下,高阶多项式函数相对于低阶多项式的训练误差应该始终更低(最坏也是相等)。事实上,当数据样本包含了 x x x的不同值时,函数阶数等于数据样本数量的多项式函数可以完美拟合训练集。下图直观地描述了多项式的阶数和欠拟合与过拟合之间的关系。

4.4.3.2 Dataset Size
另一个重要因素是数据集的大小。训练数据集中的样本越少,我们就越有可能(且更严重地)过拟合。随着训练数据量的增加,泛化误差通常会减小。一般来说,更多的数据不会有什么坏处。对于固定的任务和数据分布,模型复杂性和数据集大小之间通常存在关系。给出更多的数据,我们可能会尝试拟合一个更复杂的模型。能够拟合更复杂的模型可能是有益的。如果没有足够的数据,简单的模型可能更有用。对于许多任务,深度学习只有在有数千个训练样本时才优于线性模型。从一定程度上来说,深度学习目前的生机要归功于廉价存储、互联设备以及数字化经济带来的海量数据集。
4.4.4 Polynomial Regression
给定 x x x,我们将使用以下三阶多项式来生成训练和测试数据的标签:
y = 5 + 1.2 x − 3.4 x 2 2 ! + 5.6 x 3 3 ! + ϵ ,where ϵ ∼ N ( 0 , 0. 1 2 ) . y = 5 + 1.2x - 3.4\frac{x^2}{2!} + 5.6 \frac{x^3}{3!} + \epsilon \text{,where } \epsilon \sim \mathcal{N}(0, 0.1^2). y=5+1.2x−3.42!x2+5.63!x3+ϵ,where ϵ∼N(0,0.12).
在优化的过程中,我们通常希望避免非常大的梯度值或损失值,这就是我们将特征从 x i x^i xi调整为 x i i ! \frac{x^i}{i!} i!xi的原因。我们将为训练集和测试集各生成100个样本,具体代码如下:
import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l
import matplotlib.pyplot as pltmax_degree=20 #多项式最大阶数
n_train,n_test=100,100 #训练集和测试集大小
true_w=np.zeros(max_degree)
true_w[0:4]=np.array([5,1.2,-3.4,5.6])#generates n_train + n_test random samples from a normal distribution with mean 0 and standard deviation 1
features=np.random.normal(size=(n_train+n_test,1))
np.random.shuffle(features)
#raises each element in the features vector to the power of the corresponding degrees from 0 to max_degree - 1.
poly_features=np.power(features,np.arange(max_degree).reshape(1,-1))
for i in range(max_degree):poly_features[:,i]/=math.gamma(i+1) #gamma(n)=(n-1)!
#labels的维度:(n_train+n_test,)
labels=np.dot(poly_features,true_w)
labels+=np.random.normal(scale=0.1,size=labels.shape)#Gaussian noise is added to the labels# NumPy ndarray转换为tensor
true_w, features, poly_features, labels = [torch.tensor(x, dtype=torch.float32) for x in [true_w, features, poly_features, labels]]print(features[:2], poly_features[:2, :], labels[:2])def evaluate_loss(net, data_iter, loss): #@save"""评估给定数据集上模型的损失"""metric = d2l.Accumulator(2) # 损失的总和,样本数量for X, y in data_iter:out = net(X)y = y.reshape(out.shape)l = loss(out, y)metric.add(l.sum(), l.numel())return metric[0] / metric[1]#定义训练函数
def train(train_features, test_features, train_labels, test_labels,num_epochs=400):loss = nn.MSELoss(reduction='none')input_shape = train_features.shape[-1]# 不设置偏置,因为我们已经在多项式中实现了它net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))batch_size = min(10, train_labels.shape[0])train_iter = d2l.load_array((train_features, train_labels.reshape(-1,1)),batch_size)test_iter = d2l.load_array((test_features, test_labels.reshape(-1,1)),batch_size, is_train=False)trainer = torch.optim.SGD(net.parameters(), lr=0.01)animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',xlim=[1, num_epochs], ylim=[1e-3, 1e2],legend=['train', 'test'])for epoch in range(num_epochs):d2l.train_epoch_ch3(net, train_iter, loss, trainer)if epoch == 0 or (epoch + 1) % 20 == 0:animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),evaluate_loss(net, test_iter, loss)))print('weight:', net[0].weight.data.numpy())#三阶多项式函数拟合(正常,训练出的参数接近真实值)
# 从多项式特征中选择前4个维度,即1,x,x^2/2!,x^3/3!
train(poly_features[:n_train, :4], poly_features[n_train:, :4],labels[:n_train], labels[n_train:])
plt.show()#线性函数拟合(欠拟合)
# 从多项式特征中选择前2个维度,即1和x
train(poly_features[:n_train, :2], poly_features[n_train:, :2],labels[:n_train], labels[n_train:])
plt.show()#高阶多项式函数拟合(过拟合)
# 从多项式特征中选取所有维度
train(poly_features[:n_train, :], poly_features[n_train:, :],labels[:n_train], labels[n_train:], num_epochs=1500)
plt.show()
正常效果:

欠拟合效果:

过拟合效果:

相关文章:

《动手学深度学习(PyTorch版)》笔记4.4
注:书中对代码的讲解并不详细,本文对很多细节做了详细注释。另外,书上的源代码是在Jupyter Notebook上运行的,较为分散,本文将代码集中起来,并加以完善,全部用vscode在python 3.9.18下测试通过。…...

Linux/Academy
Enumeration nmap 首先扫描目标端口对外开放情况 nmap -p- 10.10.10.215 -T4 发现对外开放了22,80,33060三个端口,端口详细信息如下 结果显示80端口运行着http,且给出了域名academy.htb,现将ip与域名写到/et/hosts中,然后从ht…...
windows .vscode的json文件配置 CMake 构建项目 调试窗口中文设置等
一、CMake 和 mingw64的安装和环境配置 二、tasks.json和launch.json文件配置 tasks.json {"version": "2.0.0","options": {"cwd": "${workspaceFolder}/build"},"tasks": [{"type": "shell&q…...

uniapp canvas做的刮刮乐解决蒙层能自定义图片
最近给湖南中烟做元春活动,一个月要开发4个小活动,这个是其中一个难度一般,最难的是一个类似鲤鱼跃龙门的小游戏,哎,真实为难我这个“拍黄片”的。下面是主要代码。 <canvas :style"{width:widthpx,height:hei…...

利用SPI,结合数据库连接池durid进行数据服务架构灵活设计
接着上一篇文章业务开始围绕原始凭证展开,而展开的基础无疑是围绕着科目展开的。首先我们业务层面以财政部的小企业会计准则的一级科目引入软件中。下面我们来考虑如何将科目切入软件更加灵活,方便业务扩展、维护与升级。 SPI是首先想到的数据服务方式 为什么会想到它呢?首…...

自动驾驶的决策层逻辑
作者 / 阿宝 编辑 / 阿宝 出品 / 阿宝1990 自动驾驶意味着决策责任方的转移 我国2020至2025年将会是向高级自动驾驶跨越的关键5年。自动驾驶等级提高意味着对驾驶员参与度的需求降低,以L3级别为界,低级别自动驾驶环境监测主体和决策责任方仍保留于驾驶…...

排序算法——希尔排序算法详解
希尔排序算法详解 一. 引言1. 背景介绍1.1 数据排序的重要性1.2 希尔排序的由来 2. 排序算法的分类2.1 比较排序和非比较排序2.2 希尔排序的类型 二. 希尔排序基本概念1. 希尔排序的定义1.1 缩小增量排序1.2 插入排序的变种 2. 希尔排序的工作原理2.1 分组2.2 插入排序2.3 逐步…...

Docker 容器内运行 mysqldump 命令来导出 MySQL 数据库,自动化备份
备份容器数据库命令: docker exec 容器名称或ID mysqldump -u用户名 -p密码 数据库名称 > 导出文件.sql请替换以下占位符: 容器名称或ID:您的 MySQL 容器的名称或ID。用户名:您的 MySQL 用户名。密码:您的 MySQL …...

【Java万花筒】数字信号魔法:Java库的魅力解析
从傅立叶到矩阵:数字信号Java库全景剖析 前言 随着数字信号处理在科学、工程和数据分析领域的广泛应用,开发者对高效、灵活的工具的需求日益增长。本文旨在探讨几个与数字信号处理相关的Java库,通过介绍其特点、用途以及与已有库的关系&…...

面试高频知识点:2线程 2.1 线程池 2.1.2 JDK中常见的线程池实现有哪些?
1. Executors类 Executors类是线程池的工厂类,提供了一些静态方法用于创建不同类型的线程池。然而,它的使用并不推荐在生产环境中,因为它存在一些缺点,比如默认使用无界的任务队列,可能导致内存溢出。 2. ThreadPool…...
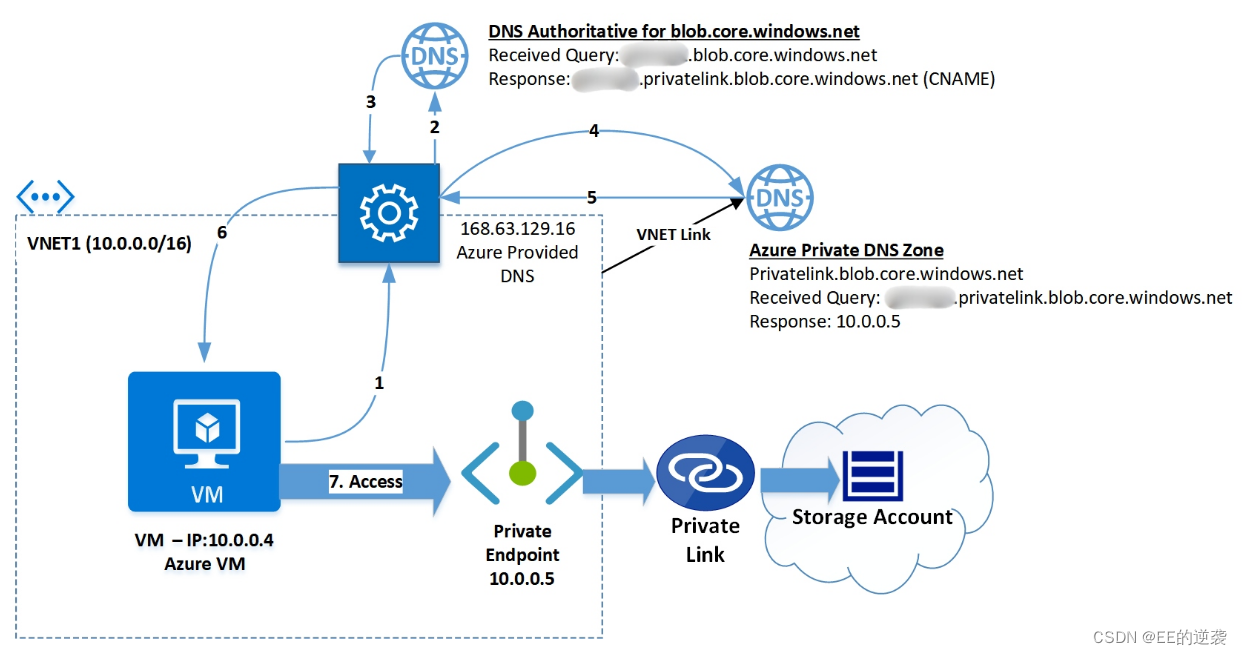
Azure Private endpoint DNS 记录是如何解析的
Private endpoint 从本质上来说是Azure 服务在Azure 虚拟网络中安插的一张带私有地址的网卡。 举例来说如果Storage account在没有绑定private endpoint之前,查询Storage account的DNS记录会是如下情况: Seq Name …...

windows 安装sql server 华为云文档
先安装net3.5,剩下安装sqlserver步骤看下面文档 安装SQL Server_弹性云服务器 ECS_最佳实践_搭建Microsoft SharePoint Server 2016_华为云 (huaweicloud.com)...

相同主题文章竟同时发表在同一个2区期刊 | 孟德尔随机化周报(1.10-1.16)
欢迎报名2024年郑老师团队课程课程! 郑老师科研统计培训,包括临床数据、公共数据分析课程,欢迎报名 孟德尔随机化,Mendilian Randomization,简写为MR,是一种在流行病学领域应用广泛的一种实验设计方法,利用…...

网络安全的使命:守护数字世界的稳定和信任
在数字化时代,网络安全的角色不仅仅是技术系统的守护者,更是数字社会的信任保卫者。网络安全的使命是保护、维护和巩固数字世界的稳定性、可靠性以及人们对互联网的信任。本文将深入探讨网络安全是如何履行这一使命的。 第一部分:信息资产的…...

【七、centos要停止维护了,我选择Almalinux】
搜索镜像 https://developer.aliyun.com/mirror/?serviceTypemirror&tag%E7%B3%BB%E7%BB%9F&keywordalmalinux dvd是有界面操作的,minimal是最小化只有命里行 镜像下载地址 安装和centos基本一样的,操作命令也是一样的,有需要我…...
架构师之路(十六)计算机网络(传输层)
前置知识(了解):计算机基础。 作为架构师,我们所设计的系统很少为单机系统,因此有必要了解计算机和计算机之间是怎么联系的。局域网的集群和混合云的网络有啥区别。系统交互的时候网络会存在什么瓶颈。 既然网络层已经…...

python 调用SumatraPDF 静默打印PDF
SumatraPDF 文档 https://www.sumatrapdfreader.org/docs/Command-line-arguments ⽆边框 noscale/缩⼩到合适⼤⼩(默认)shrink/合适⼤⼩ fit/compat 兼容 # 分为 Portrait (纵向)和 Landscape (横向)两类 https://github.com/sumatrapdfreader/sumatrap…...

nginx部署https域名ssl证书
1、在你服务器nginx文件夹下创建ssl文件夹存放证书文件和秘钥文件 把.crt和.key证书放上 2、在nginx.conf文件中配置 在nginx.conf文件中server下加入listen 443 ssl; server {listen 443 ssl;charset utf-8;index index.html index.htm index.jsp index.do;add_heade…...

Python学习之路-Django基础:HelloDjango
Python学习之路-Django基础:HelloDjango 简介 Django,发音为[dʒŋɡəʊ],是用python语言写的开源web开发框架,并遵循MVC设计。劳伦斯出版集团为了开发以新闻内容为主的网站,而开发出来了这个框架,于2005年7月在BSD…...
完成NAT实验
实验要求: 步骤一:配置vlan vlan b 2 3 interface GigabitEthernet 0/0/2 port link-type access port default vlan 2 interface GigabitEthernet 0/0/3 port link-type access port default vlan 3 interface GigabitEthernet 0/0/1 port link-type…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
