高斯消去法 | LU分解 | PA=LU分解(MatLab)
一、问题描述
利用高斯消去法,LU 分解及PA=LU 分解求解非线性方程组。
二、实验目的
掌握高斯消去法、LU 分解、PA=LU 分解的算法原理;编写代码实现利用高斯消去法、LU 分解、PA=LU 分解来求解线性方程组。
三、实验内容及要求
1. 利用顺序高斯消去法求解如下方程组。
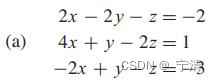
(注意将顺序高斯消去法封装为一个函数,函数名Gauss,该函数对应的文件同样命名为Gauss)。
function x = Gauss(A, b)n = length(b);for k = 1:n-1for i = k+1:nfactor = A(i,k) / A(k,k);A(i,k+1:n) = A(i,k+1:n) - factor * A(k,k+1:n);b(i) = b(i) - factor * b(k);endendx = zeros(n, 1);x(n) = b(n) / A(n,n);for i = n-1:-1:1x(i) = (b(i) - A(i,i+1:n) * x(i+1:n)) / A(i,i);end
end% 使用例子
A = [2 -2 -1; 4 1 -2; -2 1 -1];
b = [-2; 1; -3];
x = Gauss(A, b);
disp(x);
2. 对1 中的线性方程组,利用LU 分解进行求解,并输出L 和U。
(注意将本部分代码封装为一个函数,函数名LU,该函数对应的文件同样命名为LU)。
function [L, U] = LU(A)[n,~] = size(A);L = eye(n);U = A;for k = 1:n-1for i = k+1:nfactor = U(i,k) / U(k,k);L(i,k) = factor;U(i,k:n) = U(i,k:n) - factor * U(k,k:n);endend
end% 使用例子
A = [2 -2 -1; 4 1 -2; -2 1 -1];
[L, U] = LU(A);
disp(L);
disp(U);
3. 对1 中的线性方程组,利用PA=LU 分解进行求解,并输出P、L 和U。
(注意将本部分代码封装为一个函数,函数名PLU,该函数对应的文件同样命名为PLU)。
function [P, L, U] = PLU(A)[n,~] = size(A);P = eye(n);L = zeros(n);U = A;for k = 1:n-1[~, maxindex] = max(abs(U(k:n,k)));maxindex = maxindex + k - 1;U([k,maxindex],:) = U([maxindex,k],:);L([k,maxindex],1:k-1) = L([maxindex,k],1:k-1);P([k,maxindex],:) = P([maxindex,k],:);for i = k+1:nfactor = U(i,k) / U(k,k);L(i,k) = factor;U(i,k:n) = U(i,k:n) - factor * U(k,k:n);endendL = L + eye(n);
end% 使用例子
A = [2 -2 -1; 4 1 -2; -2 1 -1];
[P, L, U] = PLU(A);
disp(P);
disp(L);
disp(U);
四、算法原理
1. 给出高斯消去法、LU 分解、PA=LU 分解的算法原理
-
高斯消去法
高斯消去法是一种用于解线性方程组的算法,它的目标是将给定的系数矩阵转化为上三角矩阵(或更进一步转化为对角矩阵),这样可以直接使用回代法求解未知数。步骤:
- 选取主元(通常是当前列下的最大绝对值元素)。
- 使用主元所在的行减去其他行,从而消去该列下主元以下的所有元素。
- 对下一个列重复以上步骤,直到整个矩阵成为上三角形态。
- 使用回代法求解未知数。
-
LU 分解
LU分解是将系数矩阵A分解为一个下三角矩阵L和一个上三角矩阵U的过程。这样原方程组Ax=b变为LUx=b,先解Ly=b得到y,再解Ux=y得到x。步骤:
- 从第一行开始,将A的当前行元素存储在U的相应位置,将除对角线元素外的当前列元素存储在L的相应位置。
- 使用L的当前列元素与U的当前行元素更新A的剩余部分。
- 对于下一个列重复上述步骤。
-
PA=LU 分解
有时直接的LU分解不可能或者数值上不稳定,这时可以通过行交换获得稳定性。PA=LU分解将A分解为一个置换矩阵P、一个下三角矩阵L和一个上三角矩阵U。步骤:
- 选择一个主元并进行必要的行交换。
- 按照LU分解的方法更新L和U的元素。
- 对下一个列重复以上步骤。
2. 分别给出高斯消去法、LU 分解消去和回代过程的耗费的计算量。
-
高斯消去法
消去过程的计算量大约为(2/3)n3,而回代过程为n2。所以总的计算量大约是O(n^3)。 -
LU 分解
LU分解的计算量和高斯消去法类似,主要来自于消去过程,大约为(2/3)n3。回代过程是O(n2),所以总的计算量仍然是O(n^3)。 -
PA=LU 分解
PA=LU分解的计算量和LU分解相似,因为增加的主要是行交换操作,这不会显著增加计算量。所以总的计算量仍然是O(n^3)。
五、测试数据及结果
-
给出算法输出的方程组的解。

-
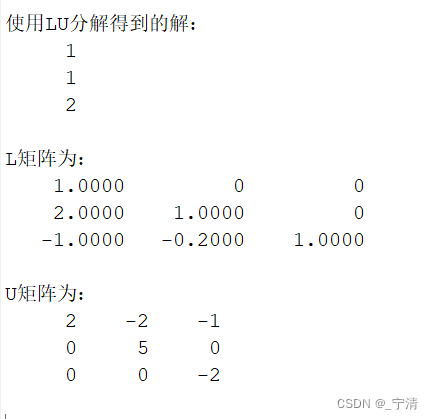
给出算法输出的方程组的解及L 和U。
-
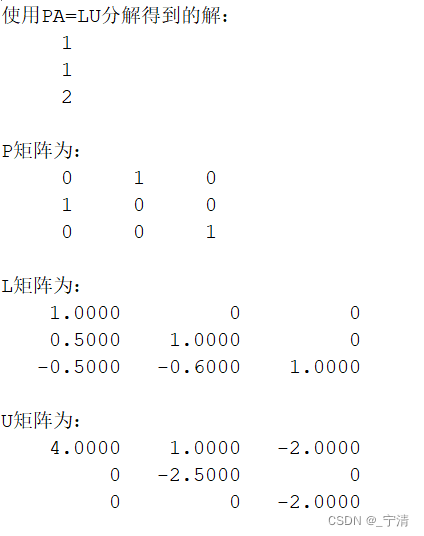
给出算法输出的方程组的解及P、L 和U。
六、总结与思考
-
知识点的理解:
通过本次MATLAB实验,我深化了对线性代数中几个关键算法的理解:高斯消去法、LU分解和PA=LU分解。这些算法是解线性方程组的基石,并且在各种应用领域中都有广泛的使用。
-
代码实现的技巧:
- 使用MATLAB进行矩阵操作相对简单。例如,我们可以轻松地进行矩阵乘法、提取子矩阵和矩阵分解。
- 通过封装代码为函数,可以使整体代码结构更清晰、模块化,并增强代码的可读性和重用性。
- 适当的注释和文档对于理解和后期修改代码非常重要。
思考:
-
算法的应用:
虽然这三种算法在解决线性方程组方面很有用,但它们在处理大型矩阵或具有特定结构的矩阵时可能并不是最优的。例如,对于稀疏矩阵或对称正定矩阵,可能存在更高效的算法。考虑不同的问题背景和矩阵特点来选择合适的算法是很重要的。
-
数值稳定性:
实验中,我们简单地实现了上述算法,但在实际应用中,数值稳定性是一个需要考虑的重要问题。特别是在高斯消去法中,如果不适当地选择主元,可能会导致数值不稳定。这就是为什么PA=LU分解(带有行交换)在某些情况下更受欢迎。
-
优化与进一步学习:
MATLAB提供了一系列的内置函数和工具箱,例如
lu函数,可以直接进行LU分解。通过比较我们自己的实现和MATLAB的内置函数,我们可以进一步了解性能和数值稳定性的问题,并从中学习。
综上,本次MATLAB实验不仅加深了我计算方法的理解,而且让我认识到在实际应用中考虑算法的数值稳定性和选择最适合的算法的重要性。
相关文章:

高斯消去法 | LU分解 | PA=LU分解(MatLab)
一、问题描述 利用高斯消去法,LU 分解及PALU 分解求解非线性方程组。 二、实验目的 掌握高斯消去法、LU 分解、PALU 分解的算法原理;编写代码实现利用高斯消去法、LU 分解、PALU 分解来求解线性方程组。 三、实验内容及要求 1. 利用顺序高斯消去法求…...

Linux笔记之expect和bash脚本监听输出并在匹配到指定字符串时发送中断信号
Linux笔记之expect和bash脚本监听输出并在匹配到指定字符串时发送中断信号 code review! 文章目录 Linux笔记之expect和bash脚本监听输出并在匹配到指定字符串时发送中断信号1.expect2.bash 1.expect 在Expect脚本中,你可以使用expect来监听程序输出,…...

项目02《游戏-12-开发》Unity3D
基于 项目02《游戏-11-开发》Unity3D , 任务:实现场景怪物自动巡航 , 首先在场景中创建小球命名为路径点WayPoint0, 取消小球的碰撞器Collider, 再复制两个改名为WayPoint1 和 WayPoint2 , 在…...

记一次面试题
1.Php 私有化包(composer)的部署 1. 创建你的PHP包 确定你的包的功能和命名空间。 创建一个新的目录并初始化一个Git仓库。 使用composer init命令创建一个composer.json文件,并定义你的包名、版本、依赖等信息。 2. 开发并测试你的包 在本地…...

Rust入门2——随机数
文章目录 一、生成随机数二、比较两个数相等 简单列出两个Rust的小例子 一、生成随机数 在Cargo.toml的dependencies中引入rand,指定rand的版本 [dependencies] rand "^0.3.14"之后在主函数中调用rand函数,生成随机数 use rand::Rng; f…...

c#: 表达式树的简化
环境: .net 6 一、问题? 有下面的表达式: var nums new List<int> { 1, 2, 3 }; Expression<Func<int, bool>> exp i > i > nums.Max();我们知道,它其实就是:exp i > i > 3; 那么…...
13. UE5 RPG限制Attribute的值的范围以及生成结构体
前面几章,我们实现了通过GameplayEffect对Attribute值的修改,比如血量和蓝量,我们都是有一个最大血量和最大蓝量去限制它的最大值,而且血量和蓝量最小值不会小于零。之前我们是没有实现相关限制的,接下来,我…...

UE4运用C++和框架开发坦克大战教程笔记(十九)(第58~60集)完结
UE4运用C和框架开发坦克大战教程笔记(十九)(第58~60集)完结 58. 弹窗显示与隐藏59. UI 面板销毁60. 框架完成与总结 58. 弹窗显示与隐藏 这节课我们先来补全 TransferMask() 里对于 Overlay 布局类型面板的遮罩转移逻辑ÿ…...

ModuleNotFoundError: No module named ‘_ctypes‘报错解决方案
1、须命令安装libbffi-devel软件包: yum install libffi-devel -y2、安装完后再重装python3,无须卸载 找到之前的python3安装包,如果安装包删除了通过 history | grep python命令找到最初安装时的包下载的命令下载,保证版本一样&…...

【服务器数据恢复】服务器RAID模块硬件损坏的数据恢复案例
服务器数据恢复环境&故障: 某品牌服务器中有一组由数块SAS硬盘组建的RAID5磁盘阵列,服务器操作系统是WINDOWS SERVER,服务器中存放企业数据,无数据库文件。 服务器出故障之前出现过几次意外断电的情况,服务器断电…...

spring boot3x登录开发-上(整合jwt)
⛰️个人主页: 蒾酒 🔥系列专栏:《spring boot实战》 🌊山高路远,行路漫漫,终有归途。 目录 前置条件 jwt简介 导依赖 编写jwt工具类 1.配置项直接嵌入代码,通过类名.静态方法使用 2.配置项写到…...

git 克隆拉取代码出现私钥权限问题。
问题反馈: rootdd:~/android/boost-1.74-for-android-r20b# git clone https://github.com/liulilittle/boost-1.74-for-android-r20b.git Cloning into boost-1.74-for-android-r20b... WARNING: UNPROTECTED PRIVATE KEY FILE! Permissions 0777 for /root/…...
【5G NR】【一文读懂系列】移动通讯中使用的信道编解码技术-卷积码原理
目录 一、引言 二、卷积编码的发展历史 2.1 卷积码的起源 2.2 主要发展阶段 2.3 重要里程碑 三、卷积编码的基本概念 3.1 基本定义 3.2 编码器框图 3.3 编码多项式 3.4 网格图(Trellis)描述 四、MATLAB示例 一、引言 卷积编码,作为数字通信领域中的一项…...

揭开Markdown的秘籍:标题|文字样式|列表
🌈个人主页:聆风吟 🔥系列专栏:Markdown指南、网络奇遇记 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. ⛳️Markdown 标题二. ⛳️Markdown 文字样式2.1 🔔斜体2.2 &…...

移动最小二乘法
移动最小二乘法(Moving Least Square,MLS)主要应用于曲线与曲面拟合,该方法基于紧支撑加权函数(即函数值只在有限大小的封闭域中定义大于零,而在域外则定义为零)和多项式基函数,通过…...

【LeetCode】37. 解数独(困难)——代码随想录算法训练营Day30
题目链接:37. 解数独 题目描述 编写一个程序,通过填充空格来解决数独问题。 数独的解法需 遵循如下规则: 数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。&…...

VUE学习——属性绑定
属性绑定,就是给html添加id、class这样类似的操作。 <template><div v-bind:id"dynamicId"><div v-bind:class"dynamicClass">Test</div></div> </template><script>export default{data(){return{…...
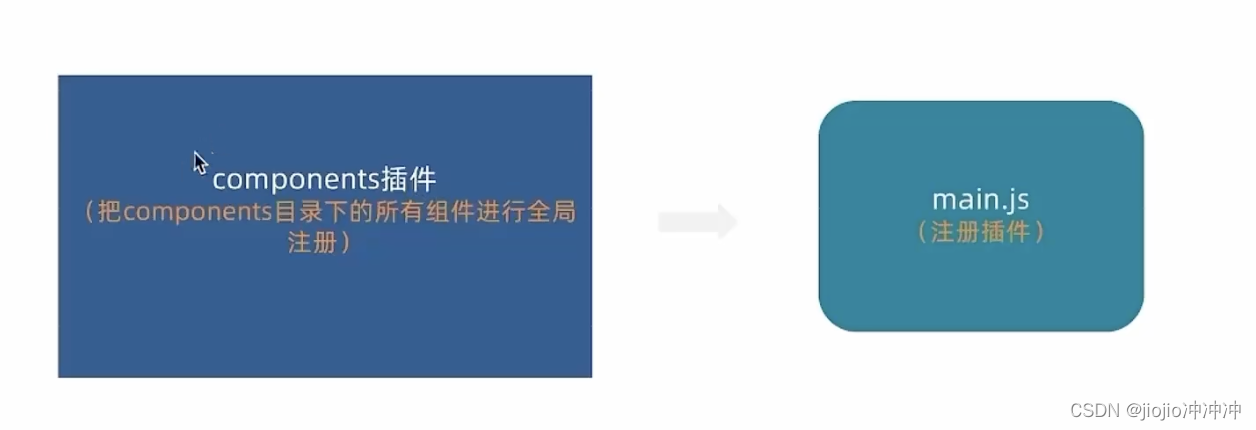
vue3 之 通用组件统一注册全局
components/index.js // 把components中的所组件都进行全局化注册 // 通过插件的方式 import ImageView from ./ImageView/index.vue import Sku from ./XtxSku/index.vue export const componentPlugin {install (app) {// app.component(组件名字,组件配置对象)…...
[Java][算法 双指针]Day 02---LeetCode 热题 100---04~07
LeetCode 热题 100---04~07 第一题:移动零 思路 找到每一个为0的元素 然后移到数组的最后 但是需要注意的是 要在给定的数组原地进行修改 并且其他非零元素的相对顺序不能改变 我们采用双指针法 定义两个指针i和j i和j一开始分别都在0索引位置 然后判断j所…...

【问题解决】如何将一个服务器的docker迁移到另一个服务器
要将Docker容器从一台机器迁移到另一台机器,可以按照以下步骤操作: 在机器A上提交容器为镜像: 使用docker commit命令将运行中的容器保存为新的镜像。这里需要容器的ID或名称,以及你想要命名的目标镜像名。 docker commit [容器…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
