【算法】排序详解(快速排序,堆排序,归并排序,插入排序,希尔排序,选择排序,冒泡排序)
目录
排序的概念:
排序算法的实现:
插入排序:
希尔排序:
选择排序:
堆排序:
冒泡排序:
快速排序:
快速排序的基本框架:
1.Hoare法
2. 挖坑法
3.前后指针法
快排的优化:
1. 三数取中法选key
2. 小区间使用插入排序
优化代码:
常见问题:
归并排序:
总结:
结语:
排序的概念:
排序:
所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持 不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳 定的;否则称为不稳定的(稳定可以转换成不稳定的,不稳定不可以转换成稳定的)。
内部排序:
数据元素全部放在内存中的排序。
外部排序:
数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
常见的排序算法:
直接插入排序,希尔排序,选择排序,堆排序,冒泡排序,快速排序,归并排序。
排序算法的实现:
说明:由于swap函数经常出现,为了使文章更加整洁,这里给出源码,下文直接调用不在说明。
private static void swap(int[] array,int i,int j){int tmp = array[i];array[i] = array[j];array[j] = tmp;}插入排序:
思路:在待排序的元素中,假设前n-1个元素已有序,现将第n个元素插入到前面已经排好的序列中,使得前n个元素有序。按照此法对所有元素进行插入,直到整个序列有序。
动图演示如下:

代码实现如下:
public static void insertSort(int[] array){for(int i = 1;i < array.length; i++){int j = i-1;int tmp = array[i];for(;j >= 0; j--){if(array[j] > tmp){array[j+1] = array[j];}else{break;}}array[j+1] = tmp;}}结果演示:

直接插入排序的特性总结:
1. 元素集合越接近有序,直接插入排序算法的时间效率越高
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1),它是一种稳定的排序算法
4. 稳定性:稳定
希尔排序:
思路:希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成多个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达 =1时,所有记录在统一组内排好序。
动图演示:
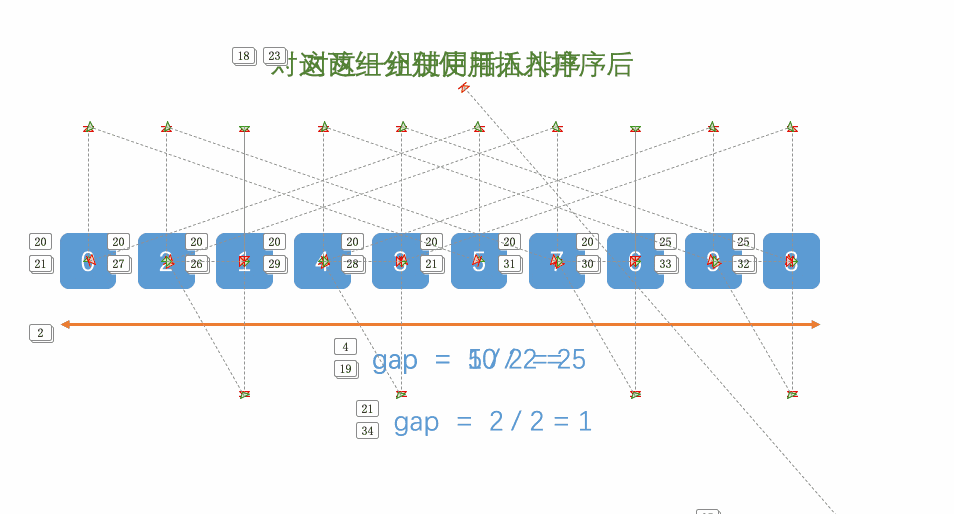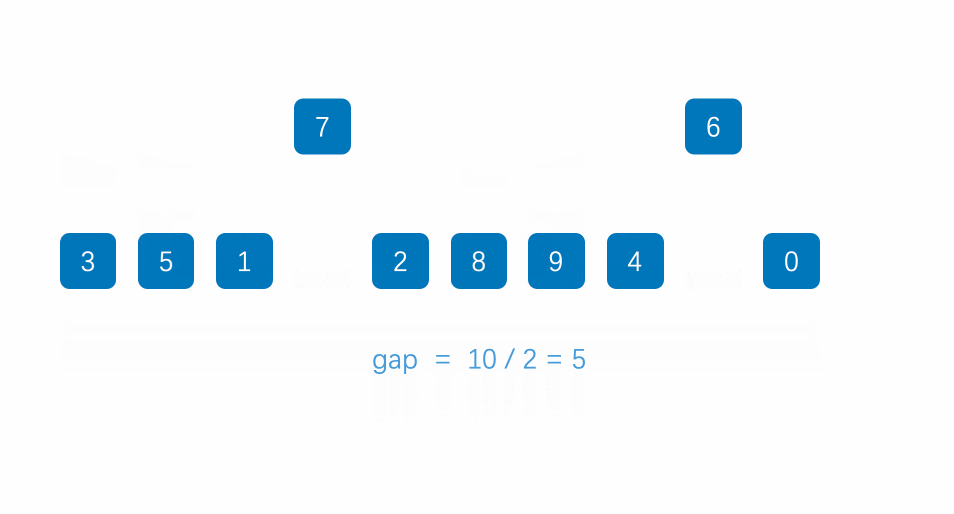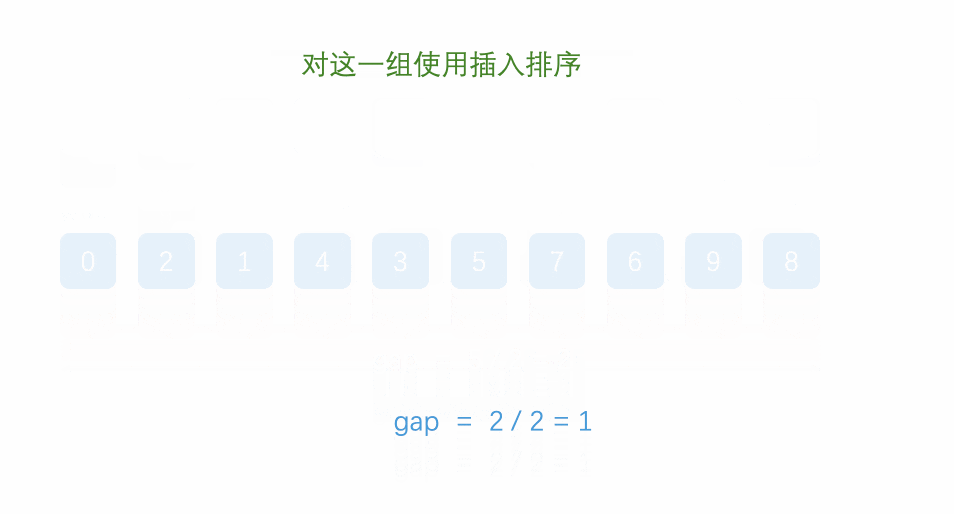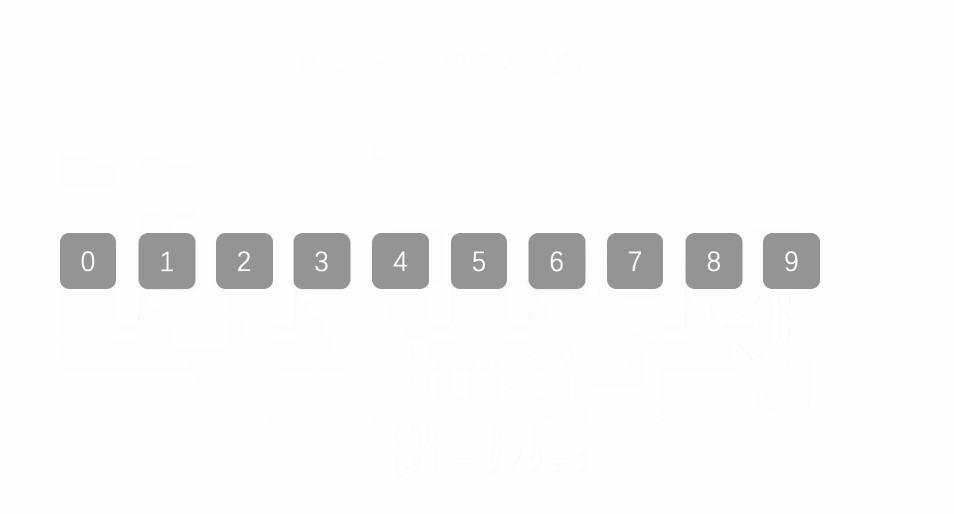
代码实现如下:
在shellSort里面确定组的大小,在shell里面进行排序,通过计算确定gap的关系,间隔运行,一次通过。
public static void shellSort(int[] array){int gap = array.length;while(gap > 1){gap /= 2;shell(array,gap);}}public static void shell(int[] array,int gap){for(int i = gap; i < array.length; i++){int j = 0;j = i-gap;int tmp = array[i];for(;j >= 0;j -= gap){if(array[j] > tmp){array[j+gap] = array[j];}else{break;}}array[j+gap] = tmp;}}结果演示:

希尔排序的特性总结:
1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很 快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
3. 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的希尔排 序的时间复杂度都不固定。
4. 稳定性:不稳定
选择排序:
思路:
(1)在元素集合array[i]--array[n-1]中选择关键码最大(小)的数据元素。
(2)若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换。
(3)在剩余的array[i]--array[n-2](array[i+1]--array[n-1])集合中,重复上述步骤,直到集合剩余1个元素。
动图演示:
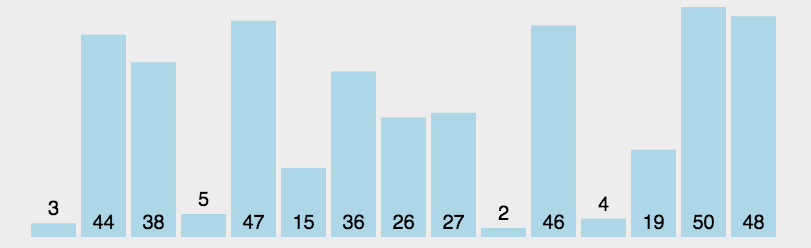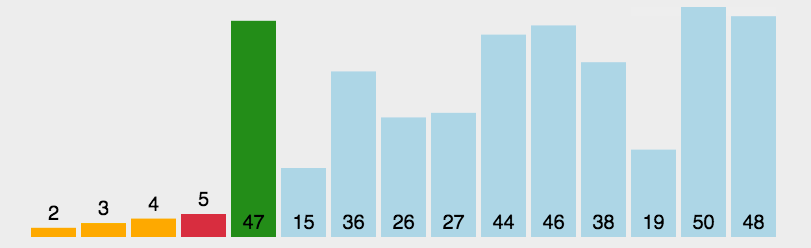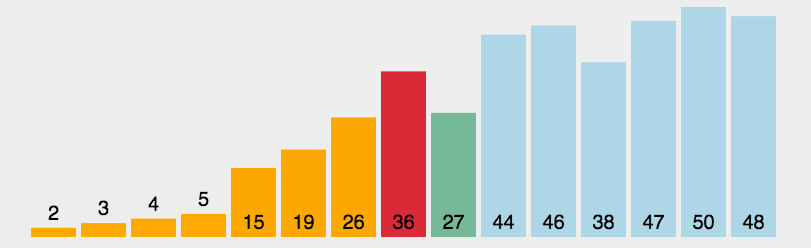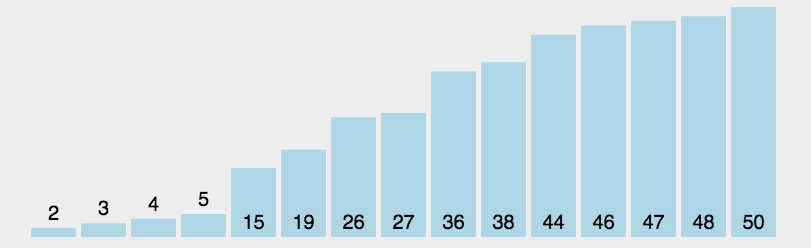
代码实现如下:
//选择排序public static void selectSort(int[] array){for(int i = 0;i < array.length-1; i++){int minIndex = i;for(int j = i+1;j < array.length; j++){if(array[j] < array[minIndex]){minIndex = j;}}swap(array,i,minIndex);}}private static void swap(int[] array,int i,int j){int tmp = array[i];array[i] = array[j];array[j] = tmp;}结果演示:

选择排序的特性总结 :
1. 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
堆排序:
思路:堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
动图演示:

代码实现如下:
从小到大用大根堆
从大到小用小根堆
下面代码为大根堆
public static void heapSort(int[] array){createBigHeap(array);int end = array.length-1;while(end > 0){swap(array,0,end);siftDown(array,0,end);end--;}}private static void createBigHeap(int[] array){for(int parent = (array.length - 1 -1)/2; parent >= 0; parent--){siftDown(array,parent,array.length);}}private static void siftDown(int[] array,int parent,int end){int child = parent*2+1;while(child < end) {if (child + 1 < end && array[child] < array[child + 1]) {child++;}if (array[child] > array[parent]) {swap(array, child, parent);parent = child;child = parent * 2 + 1;} else {break;}}}结果演示:

堆排序的特性总结:
1. 堆排序使用堆来选数,效率就高了很多。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
冒泡排序:
简单就不给思路了
动图演示:
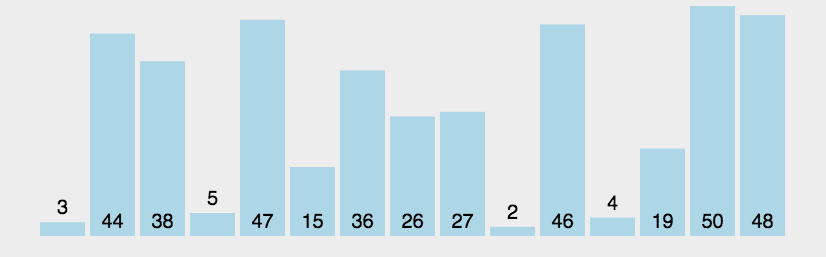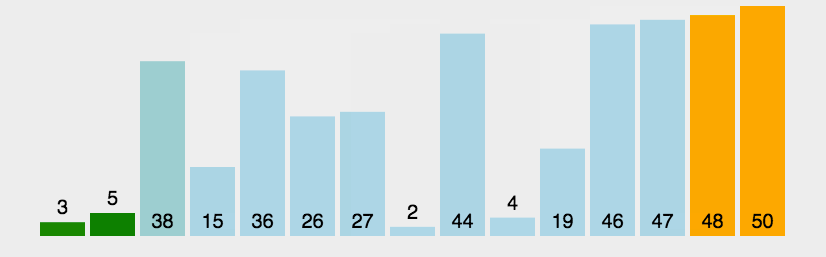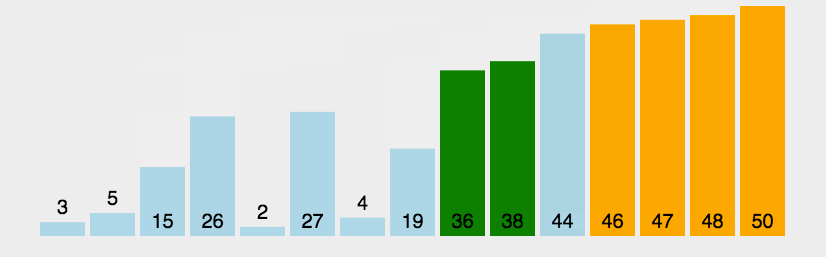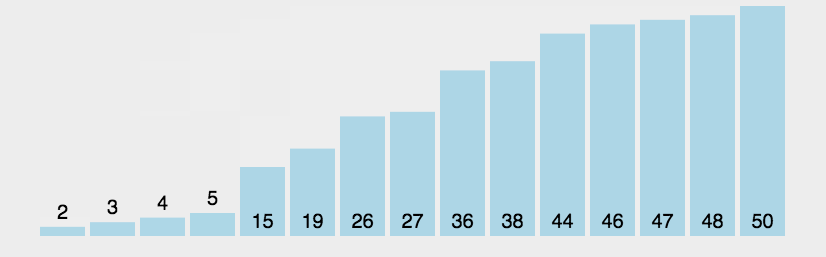
代码实现如下:
public static void bubbleSort(int[] array){for(int i = 0; i < array.length - 1; i++){boolean flg = false;for(int j = 0; j < array.length-1-i; j++){if(array[j] > array[j+1]){swap(array,j,j+1);flg = true;}}if(flg == false){return;}}}结果演示:

冒泡排序的特性总结:
1. 冒泡排序是一种非常容易理解的排序
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:稳定
快速排序:
思路:任取待排序元素序列中的某元 素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
快速排序的基本框架:
//快排的框架public static void quickSort(int[] array,int left,int right){if(right <= left){return;}int div = partition(array,left,right);quickSort(array,left,div-1);quickSort(array,div+1,right);}这是还没优化的。
partition可以得到left和right相遇的下标。
关于partition有三种求法分别是Hoare版,挖坑法,前后指针。
其中最常用的是挖坑法。
1.Hoare法
动图如下:

代码实现:
//Hoareprivate static int partition(int[] array,int left,int right){int i = left;int j = right;int pivot = array[left];while(j > i){while(j > i && array[j] >= pivot){j--;}while(j > i && array[i] <= pivot){i++;}swap(array,i,j);}swap(array,i,left);return i;}2. 挖坑法
动图如下:

代码实现:
//挖坑法private static int partition(int[] array,int left,int right){int i = left;int j = right;int pivot = array[left];while(j > i){while(j > i && array[j] >= pivot){j--;}array[i] = array[j];while(j > i && array[i] <= pivot){i++;}array[j] = array[i];}array[i] = pivot;return i;}3.前后指针法

代码如下:
//前后指针法private static int partition(int[] array,int left,int right){int prev = left;int cur = left+1;while(cur <= right){if(array[cur] < array[left] && array[++prev] != array[cur]){swap(array,cur,prev);}cur++;}swap(array,prev,left);return prev;}快排的优化:
1. 三数取中法选key
使用该优化方法可以有效减少当数组有序时变成单叉树的时间复杂度。
基本思路:选取数组中第一个数,中间数和最后一个数比较大小,将其中中间值和最左边交换,这样可以使mid左后两边数组个数尽可能相等。
代码如下:
private static int middleNum(int[] array,int left,int right){int mid = left + ((right - left) >> 1);if(array[left] < array[right]){if(array[mid] < array[left]){return left;}else if(array[mid] < array[right]){return mid;}else{return right;}}else{if(array[mid] < array[right]){return right;}else if(array[mid] < array[left]){return mid;}else{return left;}}}2. 小区间使用插入排序
思路:我们直到插入排序在数组接近有序时是非常快的,而快排最后在堆上调用的空间是非常大的,故在小区间上使用插入排序可以达到优化的效果。
代码如下:
//优化1if(right - left +1 <= 15){insertSort2(array,left,right);return;}private static void insertSort2(int[] array,int left,int right){if(left >= right){return;}for(int i = 1 + left;i <= right;i++){int tmp = array[i];//都定义可读性好int j = i-1;for(;j >= left;j--){if(array[j] > tmp){array[j+1] = array[j];}else{break;}}array[j+1] = tmp;}}优化代码:
为节省文章长度,下面个代码在上面给出,下面我就不给总代码了(抱歉)。
public static void quickSort(int[] array,int left,int right){if(right <= left){return;}//优化1if(right - left +1 <= 15){insertSort2(array,left,right);return;}//优化2int index = middleNum(array,left,right);swap(array,index,left);int div = partition(array,left,right);quickSort(array,left,div-1);quickSort(array,div+1,right);}快速排序的特性总结:
1. 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(logN)
4. 稳定性:不稳定
常见问题:
1.在partition 方法中array[j] >= pivot 和 array[i] <= pivot中的等号能否去掉?
答:不能,因为当left和right下标的值等于pivot时会陷入死循环。
2.在partition 方法中能不能先从left开始遍历?
答:不能,因为这样最后和第一个数交换时会把比pivot大的数给到第一个(假设取得pivot取的都是第一个数)
归并排序:
思路:归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使 子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
图片如下:

代码实现:
先拆分后合并用递归实现拆分,merge实现合并。
//归并排序public static void mergeSort(int[] array,int left,int right){if(left >= right){return;}int mid = left + ((right - left) >> 1);mergeSort(array,left,mid);mergeSort(array,mid+1,right);merge(array,left,mid,right);}private static void merge(int[] array,int left,int mid,int right){int s1 = left;int s2 = mid + 1;int e1 = mid;int e2 = right;int k = 0;int[] tmpArr = new int[right - left + 1];while(s1 <= e1 && s2 <= e2){if(array[s1] < array[s2]){tmpArr[k++] = array[s1++];}else{tmpArr[k++] = array[s2++];}}while(s1 <= e1){tmpArr[k++] = array[s1++];}while(s2 <= e2){tmpArr[k++] = array[s2++];}for(int i = 0;i < k;i++){array[i + left] = tmpArr[i];//特别注意要加left}}归并排序总结:
1. 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(N)
4. 稳定性:稳定
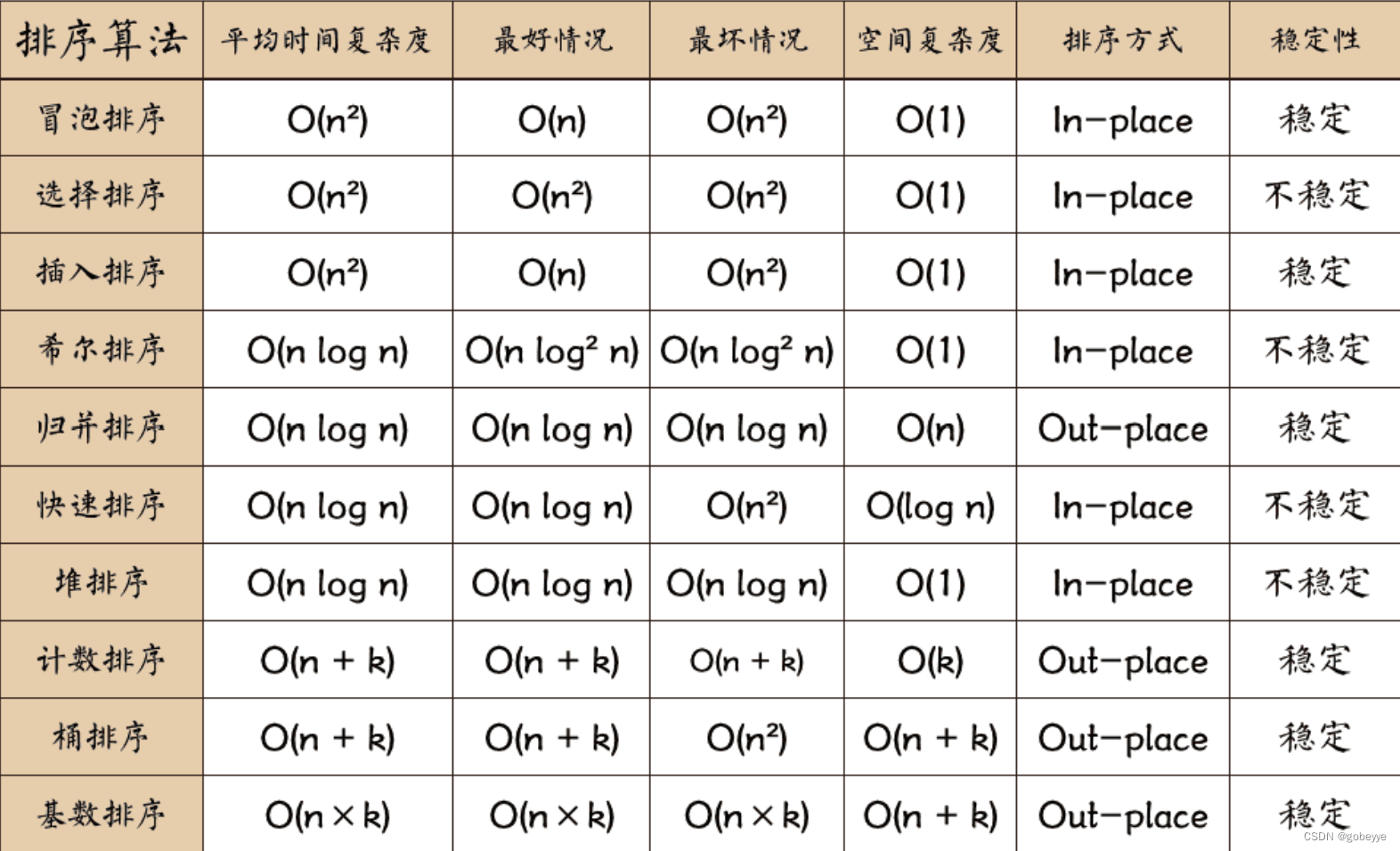
总结:
重点掌握:快排,堆排,归并,插入。
计数,基数,桶,这三个排序了解即可(代码不会写都没事不考的)

结语:
其实写博客不仅仅是为了教大家,同时这也有利于我巩固自己的知识点,和一个学习的总结,由于作者水平有限,对文章有任何问题的还请指出,接受大家的批评,让我改进,如果大家有所收获的话还请不要吝啬你们的点赞收藏和关注,这可以激励我写出更加优秀的文章。
相关文章:

【算法】排序详解(快速排序,堆排序,归并排序,插入排序,希尔排序,选择排序,冒泡排序)
目录 排序的概念: 排序算法的实现: 插入排序: 希尔排序: 选择排序: 堆排序: 冒泡排序: 快速排序: 快速排序的基本框架: 1.Hoare法 2. 挖坑法 3.前后指针法 快…...
LeetCode Python -8.字符串转整数
文章目录 题目答案运行结果 题目 请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C 中的 atoi 函数)。 函数 myAtoi(string s) 的算法如下: 读入字符串并丢弃无用的前导空格检查下一个…...
【java】笔记10:类与对象——本章练习
题目1: 代码如下: import java.util.Scanner; public class Input{public static void main(String[]args){Circle cnew Circle();PassObject yuannew PassObject();System.out.println("r""\t""times");yuan.printAreas…...

《UE5_C++多人TPS完整教程》学习笔记8 ——《P9 访问 Steam(Acessing Steam)》
本文为B站系列教学视频 《UE5_C多人TPS完整教程》 —— 《P9 访问 Steam(Acessing Steam)》 的学习笔记,该系列教学视频为 Udemy 课程 《Unreal Engine 5 C Multiplayer Shooter》 的中文字幕翻译版,UP主(也是译者&…...

缓存穿透问题与解决方案
引言 在分布式系统中,缓存技术被广泛应用以提高系统性能和响应速度。然而,缓存穿透是一个常见而严重的问题,特别是在面对大规模请求时。本文将深入探讨缓存穿透的原因、影响以及一些有效的解决方案,以确保系统在面对这一问…...

《Git 简易速速上手小册》第1章:Git 基础(2024 最新版)
文章目录 1.1 Git 简介:版本控制的演变1.1.1 基础知识讲解1.1.2 重点案例:协作开发流程优化案例:功能开发与分支策略 1.1.3 拓展案例 1:代码审查与合并1.1.4 拓展案例 2:冲突解决 1.2 安装和配置 Git:首次设…...

交易中的胜率和盈亏比估算
交易中的胜率和盈亏比估算 1.定义 胜率是指交易者在一定时间内成功交易的次数占总交易次数的比例。例如,如果交易者在10次交易中成功了6次,那么他的胜率就是60%。 盈亏比是指交易者每笔成功交易的盈利与每笔失败交易的亏损之间的比例。例如࿰…...

mysql RR、RC隔离级别实现原理
事务隔离级别实现过程 快照读(select语句) 获取事务自己版本号,即事务 ID获取 Read View 查询得到数据,然后 Read View 中事务版本号进行比较。如果不符合 Read View 可见性规则(看最新数据还是副本里的数据…...

c语言--指针数组(详解)
目录 一、什么是指针数组?二、指针数组模拟二维数组 一、什么是指针数组? 指针数组是指针还是数组? 我们类比一下,整型数组,是存放整型的数组,字符数组是存放字符的数组。 那指针数组呢?是存放…...

Elasticsearch单个索引数据量过大的优化
当Elasticsearch(ES)中的单个索引(index)的数据量变得过大时,可能会遇到性能下降、查询缓慢、管理困难等问题。为了优化和应对大索引的挑战,可以考虑以下策略: 1. 使用分片和副本 分片…...
Java安全 CC链1分析(Lazymap类)
Java安全 CC链1分析 前言CC链分析CC链1核心LazyMap类AnnotationInvocationHandler类 完整exp: 前言 在看这篇文章前,可以看下我的上一篇文章,了解下cc链1的核心与环境配置 Java安全 CC链1分析 前面我们已经讲过了CC链1的核心ChainedTransf…...
【lesson51】信号之信号处理
文章目录 信号处理可重入函数volatileSIGCHLD信号 信号处理 信号产生之后,信号可能无法被立即处理,一般在合适的时候处理。 1.在合适的时候处理(是什么时候?) 信号相关的数据字段都是在进程PCB内部。 而进程工作的状态…...
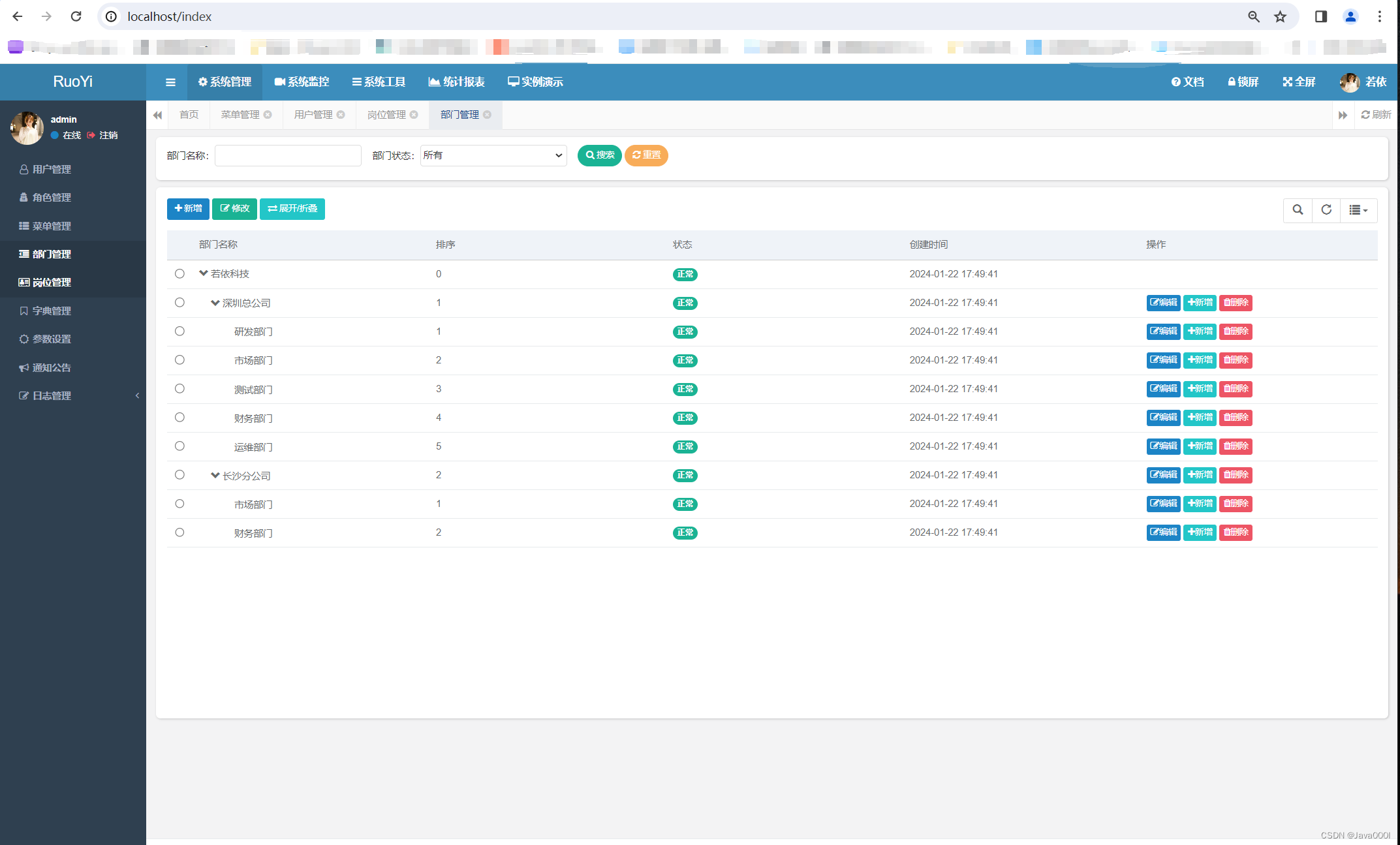
分享springboot框架的一个开源的本地开发部署教程(若依开源项目开发部署过程分享持续更新二开宝藏项目MySQL数据库版)
1首先介绍下若依项目: 若依是一个基于Spring Boot和Spring Cloud技术栈开发的多租户权限管理系统。该开源项目提供了一套完整的权限管理解决方案,包括用户管理、角色管理、菜单管理、部门管理、岗位管理等功能。 若依项目采用前后端分离的架构…...

leetcode:131.分割回文串
树形结构: 切割到字符串的尾部,就是叶子节点。 回溯算法三部曲: 1.递归的参数和返回值: 参数字符串s和startIndex切割线 2.确定终止条件: 当分割线到字符串末尾时到叶子节点,一种方案出现 3.单层搜索…...

Linux下的json-c
一、json-c库的安装(ubuntu) root用户运行以下命令: apt-get install libjson0-dev libjson0非root用户运行以下命令: sudo apt-get install libjson0-dev libjson0二、解析json数据 1. json_object json_object是JSON-C库中定义的一个结构体&#…...
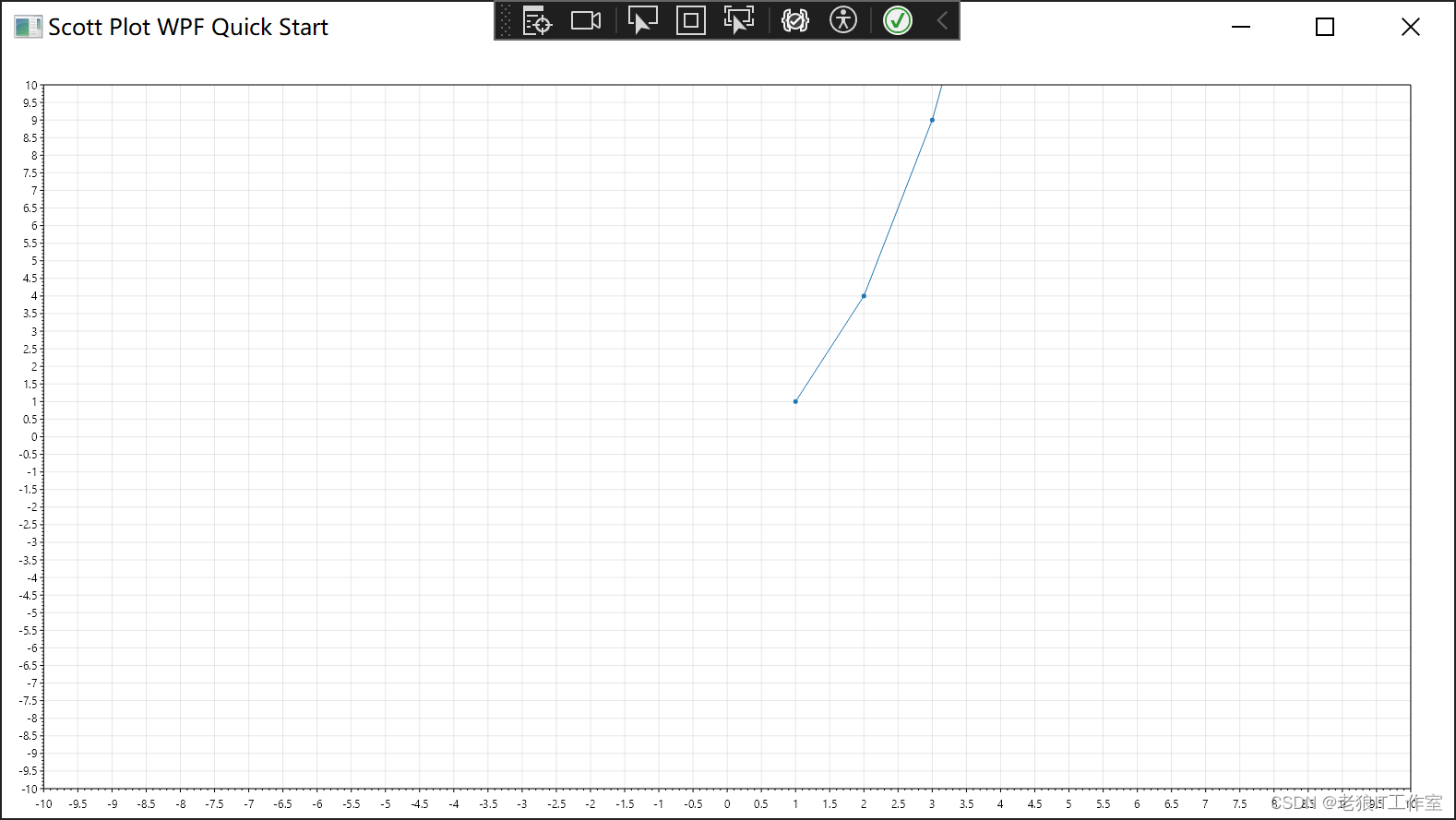
[C#] 如何使用ScottPlot.WPF在WPF桌面程序中绘制图表
什么是ScottPlot.WPF? ScottPlot.WPF 是一个开源的数据可视化库,用于在 WPF 应用程序中创建高品质的绘图和图表。它是基于 ScottPlot 库的 WPF 版本,提供了简单易用的 API,使开发人员能够通过简单的代码创建各种类型的图表&#…...
如何修复Mac的“ kernel_task” CPU使用率过高的Bug?
当计算机开始缓慢运行时,这从来都不是一件有趣的事情,但是当您弄不清它为何如此缓慢时,甚至会变得更糟。如果您已经关闭了所有程序,并且Mac上的所有内容仍然感觉像是在糖蜜中移动,这可能是令人讨厌的kernel_task导致高…...
【NodeJS】006- API模块与会话控制介绍d
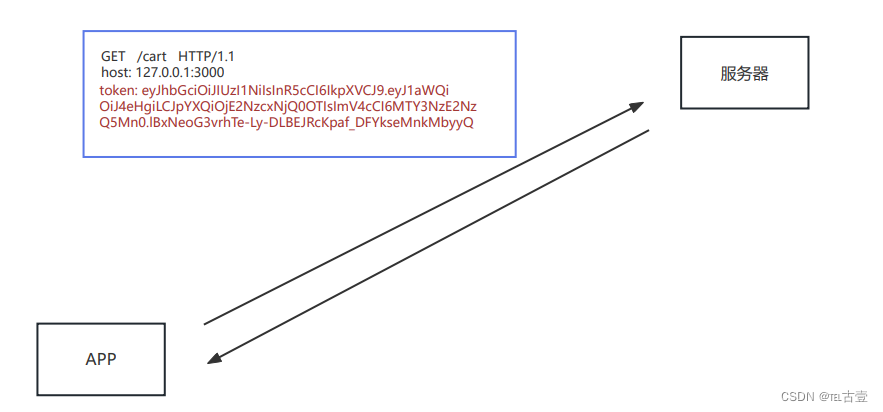
1.简介 1.1 接口是什么 接口是 前后端通信的桥梁 简单理解:一个接口就是 服务中的一个路由规则 ,根据请求响应结果 接口的英文单词是 API (Application Program Interface),所以有时也称之为 API 接口 这里的接口指的是『数据接口』&#…...

[UI5 常用控件] 08.Wizard,NavContainer
文章目录 前言1. Wizard1.1 基本结构1.2 属性1.2.1 Wizard:complete1.2.2 Wizard:finishButtonText1.2.3 Wizard:currentStep1.2.4 Wizard:backgroundDesign1.2.5 Wizard:enableBranching1.2.6 WizardStep:…...
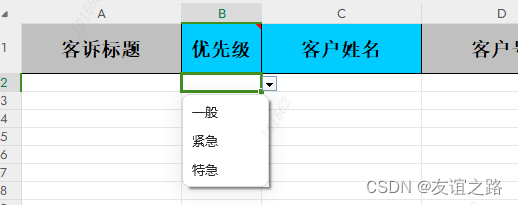
EasyExcel分页上传数据
EasyExcel分页上传数据 一、实例 controller上传入口 PostMapping("/upload")ResponseBodyLog(title "导入工单", businessType BusinessType.IMPORT)public AjaxResult uploadFile(HttpServletRequest request, MultipartFile files) throws Exceptio…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...
