线性判别分析(LDA)
一、说明
LDA 是一种监督降维和分类技术。其主要目的是查找最能分隔数据集中两个或多个类的特征的线性组合。LDA 的主要目标是找到一个较低维度的子空间,该子空间可以最大限度地区分不同类别,同时保留与歧视相关的信息。
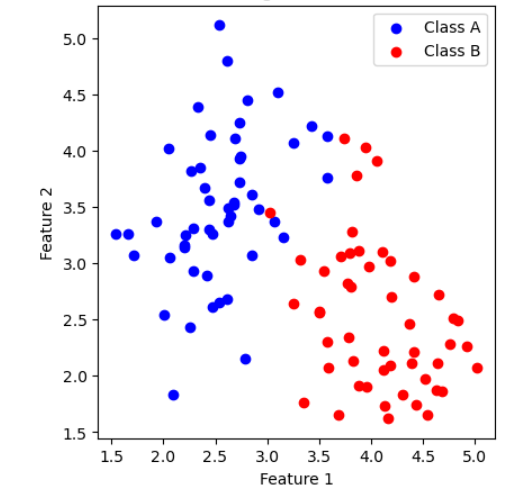
LDA 是受监督的,这意味着它需要了解类标签或类别。它试图在数据空间中找到最能区分类的方向(特征的线性组合)。LDA 使类间方差与类内方差的比率最大化。它通过查找要素的线性组合来实现,这些要素可以最大限度地提高类之间的可分离性。
然而,一个问题是,LDA与PCA有什么区别。LDA 面向分类和最大化类分离,而 PCA 则更通用,侧重于捕获数据方差
让我们看看计算数据集的 LDA 所涉及的步骤
二、步骤1:数据收集
让我们从一个数据集开始,其中包含来自两个类(A 类和 B 类)以及两个特征(特征 1 和特征 2)的样本。
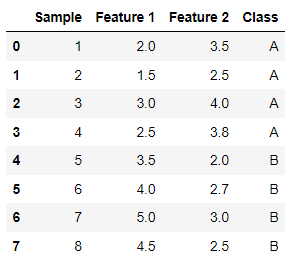
三、步骤 2:计算类均值
计算两个要素的每个类(A 类和 B 类)的平均向量。
A 类的平均向量:
Mean(Feature 1) = (2.0 + 1.5 + 3.0 + 2.5) / 4 = 2.5
Mean(Feature 2) = (3.5 + 2.5 + 4.0 + 3.8) / 4 = 3.45B 类的平均向量:
Mean(Feature 1) = (3.5 + 4.0 + 5.0 + 4.5) / 4 = 4.25
Mean(Feature 2) = (2.0 + 2.7 + 3.0 + 2.5) / 4 = 2.55四、步骤 3:计算类内散点矩阵 (SW)
SW 表示数据集的类内散点矩阵。它衡量每个类内数据的分布
要计算数据集的类内散点矩阵 (SW),您需要分别计算每个类的协方差矩阵,然后将它们相加。让我们一步一步地计算 A 类的 SW:
1.让我们将 A 类的平均向量表示为 ,我们已经计算过了:μ_A
μ_A = [Mean(Feature 1), Mean(Feature 2)] = [2.25, 3.45]2.计算A类的协方差矩阵
A 类的协方差矩阵计算如下:
Covariance Matrix for Class A (S_A) = Σ [(x - Mean Vector for Class A) * (x - Mean Vector for Class A)^T]Sample 1 (Class A):
Feature 1: 2.0
Feature 2: 3.5Calculate differences:
Diff1 = 2.0 - 2.25 = -0.25
Diff2 = 3.5 - 3.45 = 0.05Cov(Feature 1, Feature 1) = (Diff1 * Diff1) / (4 - 1) = (-0.25 * -0.25) / 3 = 0.0417
Cov(Feature 1, Feature 2) = (Diff1 * Diff2) / (4 - 1) = (-0.25 * 0.05) / 3 = -0.0042 Sample 2 (Class A):
Feature 1: 1.5
Feature 2: 2.5Calculate differences:
Diff1 = 1.5 - 2.25 = -0.75
Diff2 = 2.5 - 3.45 = -0.95Covariance Matrix elements for Sample 2:
Cov(Feature 1, Feature 1) = (Diff1 * Diff1) / (4 - 1) = (-0.75 * -0.75) / 3 = 0.1875
Cov(Feature 1, Feature 2) = (Diff1 * Diff2) / (4 - 1) = (-0.75 * -0.95) / 3 = 0.2375Sample 3 (Class A):Feature 1: 3.0
Feature 2: 4.0
Calculate differences:Diff1 = 3.0 - 2.25 = 0.75
Diff2 = 4.0 - 3.45 = 0.55
Covariance Matrix elements for Sample 3:Cov(Feature 1, Feature 1) = (Diff1 * Diff1) / (4 - 1) = (0.75 * 0.75) / 3 = 0.1875
Cov(Feature 1, Feature 2) = (Diff1 * Diff2) / (4 - 1) = (0.75 * 0.55) / 3 = 0.1375Sample 4 (Class A):Feature 1: 2.5
Feature 2: 3.8
Calculate differences:Diff1 = 2.5 - 2.25 = 0.25
Diff2 = 3.8 - 3.45 = 0.35Covariance Matrix elements for Sample 4:
Cov(Feature 1, Feature 1) = (Diff1 * Diff1) / (4 - 1) = (0.25 * 0.25) / 3 = 0.04
Cov(Feature 1, Feature 2) = (Diff1 * Diff2) / (4 - 1) = (0.25 * 0.35) / 3 = 0.029A 类的协方差矩阵:
| Cov(Feature 1, Feature 1) Cov(Feature 1, Feature 2) |
| Cov(Feature 2, Feature 1) Cov(Feature 2, Feature 2) |Covariance Matrix for Sample 1 (S1_A):
[[0.25, -0.025],[-0.025, 0.0025]]Covariance Matrix for Sample 2 (S2_A):
[[1.0, 0.95],[0.95, 0.9025]]Covariance Matrix for Sample 3 (S3_A):
[[0.25, 0.275],[0.275, 0.3025]]Covariance Matrix for Sample 4 (S4_A):
[[0.0, 0.0],[0.0, 0.1225]]S_A = S1_A + S2_A + S3_A + S4_A代入计算值:
S_A =| 0.0417 -0.0042 || 0.2375 0.0417 |同样,我们可以计算 B 类的协方差矩阵
Sample 5 (Class B):
Cov(Feature 1, Feature 1) = (Diff1 * Diff1) = (-0.625 * -0.625) = 0.390625
Cov(Feature 1, Feature 2) = (Diff1 * Diff2) = (-0.625 * -0.55) = 0.34375
Cov(Feature 2, Feature 1) = (Diff2 * Diff1) = (-0.55 * -0.625) = 0.34375
Cov(Feature 2, Feature 2) = (Diff2 * Diff2) = (-0.55 * -0.55) = 0.3025Sample 6 (Class B):
Cov(Feature 1, Feature 1) = (Diff1 * Diff1) = (-0.125 * -0.125) = 0.015625
Cov(Feature 1, Feature 2) = (Diff1 * Diff2) = (-0.125 * 0.15) = -0.01875
Cov(Feature 2, Feature 1) = (Diff2 * Diff1) = (0.15 * -0.125) = -0.01875
Cov(Feature 2, Feature 2) = (Diff2 * Diff2) = (0.15 * 0.15) = 0.0225Sample 7 (Class B):
Cov(Feature 1, Feature 1) = (Diff1 * Diff1) = (0.875 * 0.875) = 0.765625
Cov(Feature 1, Feature 2) = (Diff1 * Diff2) = (0.875 * 0.45) = 0.39375
Cov(Feature 2, Feature 1) = (Diff2 * Diff1) = (0.45 * 0.875) = 0.39375
Cov(Feature 2, Feature 2) = (Diff2 * Diff2) = (0.45 * 0.45) = 0.2025Sample 8 (Class B):
Cov(Feature 1, Feature 1) = (Diff1 * Diff1) = (0.375 * 0.375) = 0.140625
Cov(Feature 1, Feature 2) = (Diff1 * Diff2) = (0.375 * -0.05) = -0.01875
Cov(Feature 2, Feature 1) = (Diff2 * Diff1) = (-0.05 * 0.375) = -0.01875
Cov(Feature 2, Feature 2) = (Diff2 * Diff2) = (-0.05 * -0.05) = 0.0025S_B = S5_B + S6_B + S7_B + S8_BS_B = [[1.3125, 0.7],[0.7, 0.53]]计算类内散点矩阵 (SW)。将两个类的协方差矩阵相加即可得到 SW:
Within-Class Scatter Matrix (SW)
=S_A+S_B=S_W
= [0.0833 + 0.765625, -0.000833 + 0.39375][-0.000833 + 0.39375, 0.0025 + 0.2025]S_W = [0.848925, 0.393917][0.392917, 0.205]五、步骤 4:计算特征值和特征向量
在计算上,可以找到:
# Compute eigenvalues and eigenvectors
eigenvalues, eigenvectors = np.linalg.eig(S_W)从数学上讲,这可以找到:
- 计算S_W的倒数:
计算类内散点矩阵的逆数,表示为 S_W⁻¹。如果S_W不可逆,则可以使用伪逆。
S_W^(-1) = | 10.8103 -20.7762 || -20.7762 44.7628 |2.S_W^(-1)和S_B的乘积
S_W^(-1) * S_B = | 13.344 -6.953 || -4.543 11.953 |3.To 找到特征值 (λ),您需要求解特征方程,该方程由下式给出:
|S_W^(-1) * S_B - λ * I| = 0I是单位矩阵
| 13.344 - λ -6.953 |
| -4.543 11.953 - λ | 可以通过将每个特征值代入方程并求解相应的特征向量来找到特征向量。S_W^(-1) * S_B * v = λ * vv
六、步骤 5:对特征值进行排序
获得特征值后,按降序对它们进行排序以确定其重要性。您可以按如下方式在数学上表示这一点:
设特征值表示为 λ_1、λ_2、...、λ_p (其中 p 是要素或维度的数量)。
按降序对特征值进行排序:
λ_1 >= λ_2 >= ... >= λ_p七、第 6 步:选择组件
现在,您可以选择顶部特征值,其中是所需的降维水平。让我们将其表示为选择最大的特征值:kkk
λ_1, λ_2, ..., λ_k 这些特征值表示数据中最重要的判别方向。k
八、第 7 步:项目数据
选择特征值后,可以使用相应的特征向量将原始数据投影到新的低维空间上。此步骤降低了数据的维度,同时保留了最相关的信息。kk
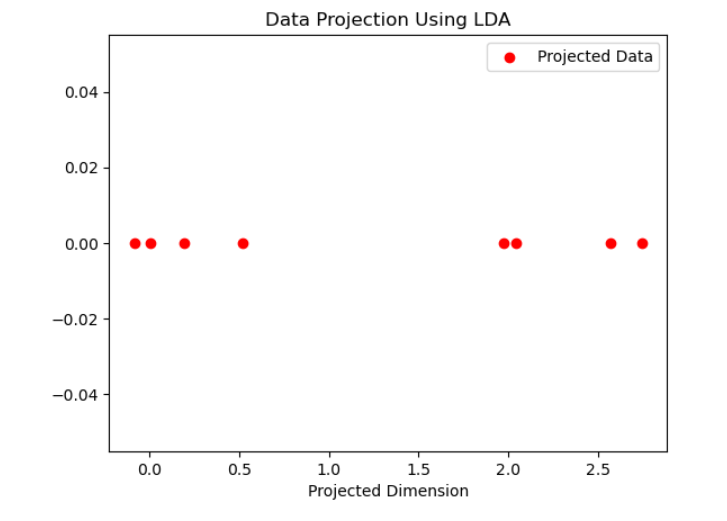
使用线性判别分析 (LDA) 中选定的特征向量将数据投影到低维空间上
相关文章:

线性判别分析(LDA)
一、说明 LDA 是一种监督降维和分类技术。其主要目的是查找最能分隔数据集中两个或多个类的特征的线性组合。LDA 的主要目标是找到一个较低维度的子空间,该子空间可以最大限度地区分不同类别,同时保留与歧视相关的信息。 LDA 是受监督的,这意…...

Vue 前置导航
Vue 前置导航(Vue Front Navigation)是一种在 Vue.js 框架中实现导航功能的常见方式。它通常用于构建单页应用程序(Single Page Application),通过在页面顶部或侧边栏显示导航菜单,使用户能够轻松切换到不同…...

串行通信,并行通信,波特率,全双工,半双工,单工等通信概念
串行通信: 只使用一根线来进行数据发送或者是接收,串行通信传输数据是一位一位进行传输 并行通信: 使用多跟线进行数据的发送和接收,并行通信可以一次传输多个数据位 波特率: 每秒传输数据的位数,决定…...
鸿蒙系统进一步学习(一):学习资料总结,少走弯路
随着鸿蒙Next的计划越来越近,笔者之前的鸿蒙系统扫盲系列中,有很多朋友给我留言,不同的角度的问了一些问题,我明显感觉到一点,那就是许多人参与鸿蒙开发,但是又不知道从哪里下手,因为资料太多&a…...

异步复位同步释放原则
复位信号有一个非常重要的原则,叫作异步复位同步释放原则。异步复位指一个寄存器的复位信号随时可以复位,不必考虑该寄存器的时钟信号正处在哪个相位上。同步释放是指一个寄存器的复位信号从复位态回到释放态的时机,必须与该寄存器的时钟信号…...
M1 Mac使用SquareLine-Studio进行LVGL开发
背景 使用Gui-Guider开发遇到一些问题,比如组件不全。使用LVGL官方的设计软件开发 延续上一篇使用的基本环境。 LVGL项目 新建项目 选择Arduino的项目,设定好分辨率及颜色。 设计UI 导出代码 Export -> Create Template Project 导出文件如图…...
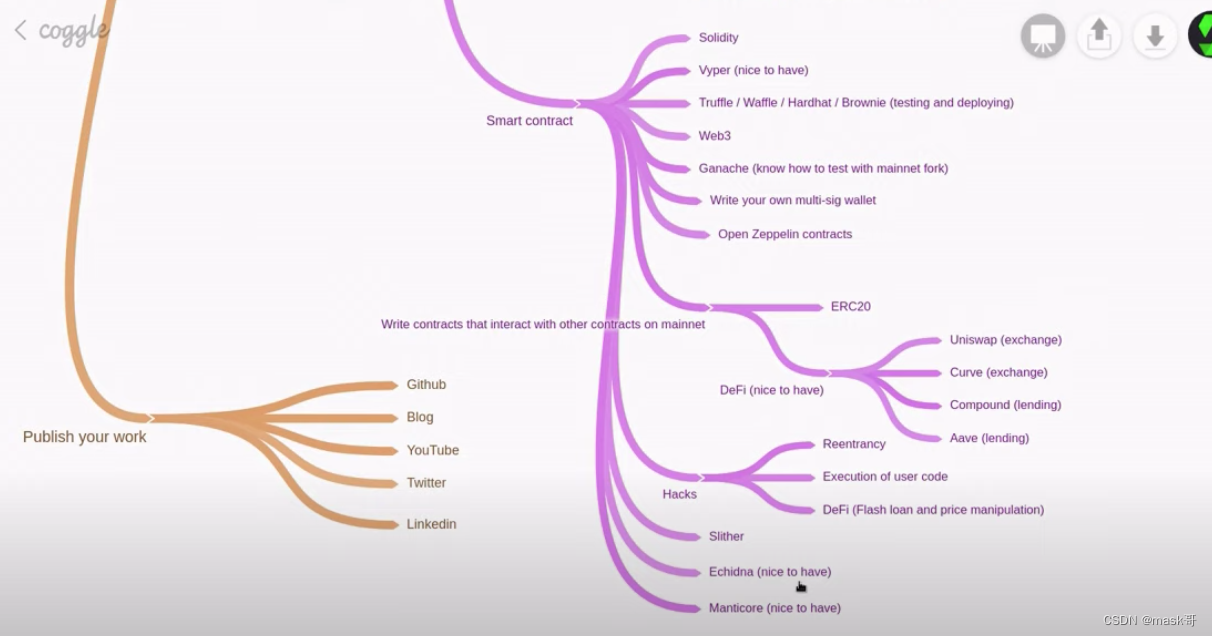
web3知识体系汇总
web3.0知识体系 1.行业发展 2. web3的特点: 1、统一身份认证系统 2、数据确权与授权 3、隐私保护与抗审查 4、去中心化运行 Web3.0思维技术思维✖金融思维✖社群思维✖产业思维”,才能从容理解未来Web3.0时代的大趋势。 3.技术栈 Web3.jsSolidit…...

服务器与电脑的区别?
目录 一、什么是服务器 二、什么是电脑 三、服务器和电脑的区别 一、什么是服务器 服务器是指一种专门提供计算和存储资源、运行特定软件服务的物理或虚拟计算机。服务器主要用于接受和处理来自客户端(如个人电脑、手机等)的请求,并向客户…...

结束 代码随想录 链表章节(下一张
环形链表II 首先,先判断有没有环,像物理相对速度一样 只要 相对速度为1 那么快指针绝对会在环里追上慢指针,最后x 和z 的距离其实最后两个index总会相遇,相遇的点就是入口 class Solution { public:ListNode *detectCycle(List…...

re:从0开始的CSS学习之路 6. 字体相关属性
1. 字体相关属性 font-size 字体大小 font-family 字体的系列(字体簇) 可以设置多个字体,每个字体之间以逗号隔开 设置多个字体的目的是为了用户尽可能的支持字体 网页字体的五大类: serif 衬线字体 sans-serif 非衬线字体 monos…...

FPGA(基于xilinx)中PCIe介绍以及IP核XDMA的使用
Xilinx中PCIe简介以及IP核XDMA的使用 例如:第一章 PCIe简介以及IP核的使用 文章目录 Xilinx中PCIe简介以及IP核XDMA的使用一、PCIe总线概述1.PCIe 总线架构2.PCIe 不同版本的性能指标及带宽计算3.PCIe 接口信号 二、XDMA1.XDMA 与其它 PCIe IP 的区别2.XDMA简介 三…...

docker 运行jar包 指定配置文件
要在Docker中运行JAR包并指定配置文件,你可以创建一个Dockerfile来定义你的容器环境,并在其中指定如何运行JAR包和配置文件。下面是一个简单的例子,展示了如何在Dockerfile中设置这些配置: 第一步:创建 Dockerfile文件…...

‘vue-cli-service‘ 不是内部或外部命令,也不是可运行的程序
遇到 vue-cli-service 不是内部或外部命令,也不是可运行的程序或批处理文件。 的错误时,通常意味着Vue CLI没有被正确安装或配置在项目中。这可能是因为node_modules目录缺失了必要的包,或者局部安装的Vue CLI没有被正确设置到系统的PATH环境…...
第9讲用户信息修改实现
用户信息修改实现 后端修改用户昵称: /*** 更新用户昵称* param wxUserInfo* param token* return*/ RequestMapping("/updateNickName") public R updateNickName(RequestBody WxUserInfo wxUserInfo,RequestHeader String token){if(StringUtil.isNot…...

powershell 离线安装Posh-SSH
PowerShell 离线安装 Posh-SSH 模块,可以按照以下步骤进行: 从可靠的来源获取 Posh-SSH 模块的 NuGet 安装包(.nupkg 文件)。确保该安装包是最新版本,并且与你的 PowerShell 版本兼容。将 NuGet 安装包复制到你的计算…...
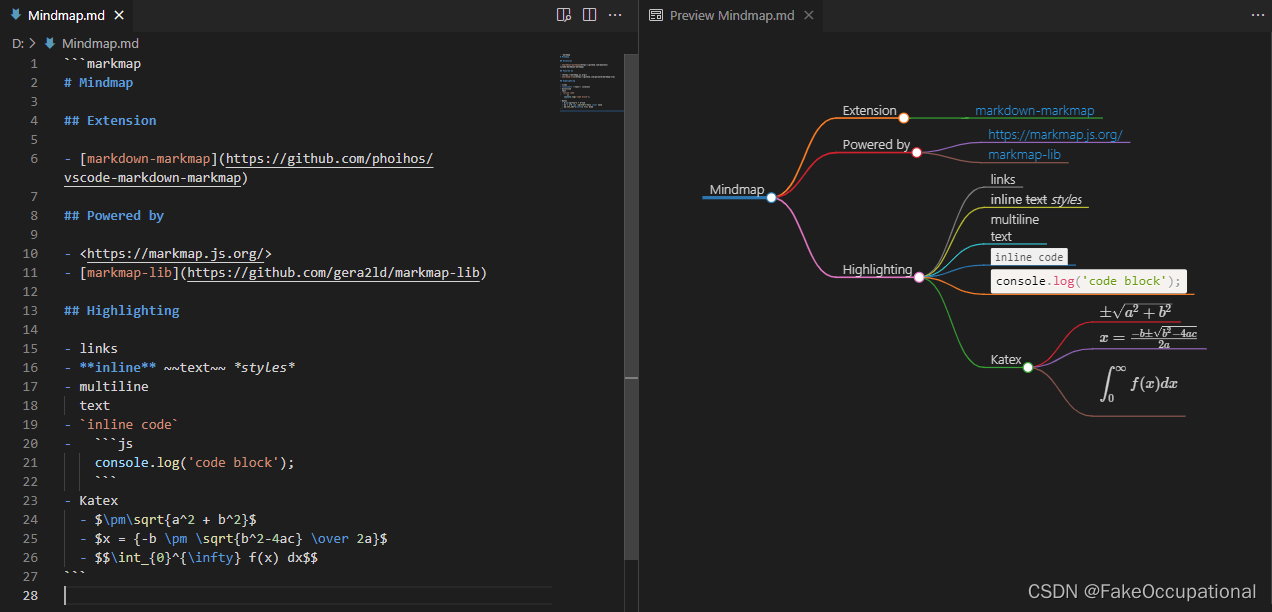
linux系统下vscode portable版本的c++/Cmake环境搭建002:使用 VSIX 安装VSCODE插件(暂记)
使用 VSIX 安装VSCODE插件 在 Visual Studio Code (VSCode) 中,你可以通过以下步骤离线安装插件: 获取插件的 VSIX 文件: 在一个联网环境中,访问 Visual Studio Code Marketplace,搜索并找到你想要的插件。 比如&am…...

PHP特性知识点总结
如果想观感更好看到图片,可以去我的gitbook或者github去看 github:https://github.com/kakaandhanhan/cybersecurity_knowledge_book-gitbook.22kaka.fun gitbook:http://22kaka.fun description: 专门出的关于php的特性比较,后面好像也有java的特性。 🏀 PHP特性知识点…...

数据库基本操作
一.DDL(Data Definition Language) 数据定义语言,该语言包括以下部分: 对数据库的常用操作对表结构的常用操作修改表结构 不涉及数据 不区分大小写 二.对数据库的常用操作 1.查看所有的数据库 show databases; 2.创建数据…...

【51单片机】矩阵键盘(江科大)
6.1矩阵键盘 矩阵键盘: 在键盘中按键数量较多时,为了减少I/O口的占用,通常将按键排列成矩阵形式 采用逐行或逐列的“扫描”,就可以读出任何位置按键的状态 1.数码管扫描(输出扫描) 原理:显示第1位→显示第2位→显示第3位→ …… ,然后快速循环这个过程,最终实现所…...
起源)
Go语言教学(一)起源
目录 一.Go语言来源 二.Go语言应用 一.Go语言来源 Go语言,又称Golang,是Google公司于2009年11月正式对外公开的一门编程语言。它是一门静态强类型、编译型的语言,其语法与C相近,但在功能上有所改进和增加,如内存安全…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
