Educational Codeforces Round 160 (Rated for Div. 2) E. Matrix Problem(费用流)
原题链接:E. Matrix Problem
题目大意:
给出一个 n n n 行 m m m 列的 0 / 1 0/1 0/1 矩阵,再给出一些限制条件:一个长为 n n n 的数组 a a a,和一个长为 m m m 的数组 b b b 。
其中 a i a_{i} ai 表示第 i i i 行要有 恰好 a i a_{i} ai 个 1 1 1 , b j b_{j} bj 表示第 j j j 列要有 恰好 b j b_{j} bj 个 1 1 1 ,保证 1 ≤ a i ≤ m , 1 ≤ b j ≤ n 1 \leq a_{i} \leq m,1 \leq b_{j} \leq n 1≤ai≤m,1≤bj≤n 。
你可以使用 任意多次 操作,将一个 0 0 0 翻转成 1 1 1 ,或将 1 1 1 翻转成 0 0 0 。
问最少的操作次数是多少,才能使得这个矩阵满足以上 a , b a,b a,b 限制,如果怎么操作都不能满足以上限制则输出 − 1 -1 −1 。
解题思路:
套路的,我们将行和列看成点,行为左部,列为右部,而每个位置 ( i , j ) (i,j) (i,j) 的信息看成是一条 i i i 和 j j j 的边,这样我们的矩阵就会形成一张天然的二分图。
回到这一题,首先要是连 ∑ i = 1 n a i ≠ ∑ i = 1 m b i \sum_{i=1}^{n} a_{i} \neq \sum_{i=1}^{m} b_{i} ∑i=1nai=∑i=1mbi 了,那肯定无论如何都不会满足的,但只有这个条件是不够的,而且很容易找出反例,但我们可以先判掉,使得接下来 ∑ i = 1 n a i = ∑ i = 1 m b i \sum_{i=1}^{n} a_{i} = \sum_{i=1}^{m} b_{i} ∑i=1nai=∑i=1mbi ,方便后续讨论。
考虑全是 0 0 0 我们怎么做,本质上就是每条边流量为 1 1 1 ,源点 S → [ 1 , 2 , . . . , n ] S \rightarrow [1,2,...,n] S→[1,2,...,n] 连一条流量为 a i a_{i} ai 的边, [ 1 , 2 , . . . , m ] → [1,2,...,m] \rightarrow [1,2,...,m]→ 汇点 T T T 连一条流量为 b i b_{i} bi 的边,然后跑一个最大流即可。
当我们发现最大流和 ∑ i = 1 n a i \sum_{i=1}^{n} a_{i} ∑i=1nai 不等,那么显然无论如何操作也是不行的。
(其实本质上就是在做一个匹配的操作:点 A A A 可以匹配 a i a_{i} ai 个人,点 B B B 可以匹配 b i b_{i} bi 个人,看是否使得每个人都能匹配完全)
但是这一题是带操作次数的条件的,我们要最小操作次数,而且矩阵初始值也不是全为 0 0 0 ,这要怎么办?
首先考虑 0 0 0 的位置的影响,如果某个地方的 0 0 0 无论如何都要翻转为 1 1 1 的,那么这个 0 0 0 对操作的贡献是固定为 1 1 1 的,我们直接操作就好。而其他无所谓的 0 0 0 显然去操作只会让操作数变多,不优。
再考虑 1 1 1 的位置的影响,无论如何我们都要把多余的 1 1 1 给删掉,我们不妨先全部删除了,操作数就是 1 1 1 的个数。再考虑哪些 1 1 1 是可以作为选择的,然后反悔我们的删除操作,把这个 1 1 1 加回来即可,这样对我们操作的贡献是为 − 1 -1 −1 的。
按照上面的转化,假设矩阵为 g n , m g_{n,m} gn,m 那么:
- 先假设矩阵全为 0 0 0 ,统计 1 1 1 的个数。
- 当 g i , j = 1 g_{i,j}=1 gi,j=1 时,我们添加边 i → j i \rightarrow j i→j ,流量为 1 1 1,费用为 − 1 -1 −1 (反悔)。
- 当 g i , j = 0 g_{i,j}=0 gi,j=0 时,我们添加边 i → j i \rightarrow j i→j ,流量为 1 1 1,费用为 1 1 1 (固定)。
- S S S 向 i i i 连上流量为 a i a_{i} ai,费用为 0 0 0 的边, j j j 向 T T T 连上流量为 b j b_{j} bj,费用为 0 0 0 的边。
- 这里的 i , j i,j i,j 分别指的是 左部 的点的编号和 右部 的点的编号。
如果最大流不为 ∑ i = 1 n a i \sum_{i=1}^{n} a_{i} ∑i=1nai 说明不能匹配完全,输出 − 1 -1 −1 。
否则我们所需要的最小操作次数就是 ∑ i = 1 n ∑ j = 1 m g i , j + \sum_{i=1}^{n}\sum_{j=1}^{m}g_{i,j}+ ∑i=1n∑j=1mgi,j+ 最小费用 (固定 + + + 反悔的和)。
代码使用的是 S p f a + D i n i c Spfa+Dinic Spfa+Dinic 的费用流。
时间复杂度: O ( n 3 m 3 ) O(n^{3}m^{3}) O(n3m3) (伪多项式复杂度,可以通过)
AC代码:
#include <bits/stdc++.h>
using namespace std;using PII = pair<int, int>;
using i64 = long long;template<class Ty>
struct MCmaxFlow {const Ty INF = numeric_limits<Ty>::max();int S, T, n; Ty MF = 0, MC = 0;struct Edge {int v, nxt; Ty f, w;Edge() : Edge(0, 0, 0, 0) {};Edge(int v, int nxt, Ty f, Ty w) : v(v), nxt(nxt), f(f), w(w) {};};vector<Ty> dist;vector<int> cur, h;vector<bool> vis;vector<Edge> E;MCmaxFlow(int _) : n(_) { init(_); };void init(int _) {dist.resize(_ + 1);vis.resize(_ + 1);cur.resize(_ + 1);h.resize(_ + 1);E.resize(2);}void add(int u, int v, Ty f, Ty w) {E.emplace_back(v, h[u], f, w), h[u] = int(E.size()) - 1;}void addEdge(int u, int v, Ty f, Ty w) {add(u, v, f, w), add(v, u, 0, -w);}bool SPFA() {dist.assign(n + 1, INF);queue<int> que;dist[S] = 0, cur[S] = h[S];que.push(S);while (que.size()) {int u = que.front(); que.pop();vis[u] = false;for (int i = h[u]; i; i = E[i].nxt) {auto& [v, nxt, f, w] = E[i];if (f && dist[v] > dist[u] + w) {dist[v] = dist[u] + w;if (!vis[v]) {vis[v] = true;cur[v] = h[v];que.push(v);}}}}return dist[T] != INF;}Ty DFS(int u, Ty flow) {if (u == T) return flow;Ty last = flow;vis[u] = true;for (int i = cur[u]; i && last; i = E[i].nxt) {cur[u] = i;auto& [v, nxt, f, w] = E[i];if (f && !vis[v] && dist[v] == dist[u] + w) {Ty cost = DFS(v, min(f, last));if (!cost) dist[v] = INF;E[i].f -= cost, E[i ^ 1].f += cost;last -= cost;}}vis[u] = false;return flow - last;}void work() {while (SPFA()) {Ty flow = DFS(S, INF);MC += dist[T] * flow;MF += flow;}}
};void solve() {int n, m;cin >> n >> m;MCmaxFlow<int> G(n + m + 2);vector g(n + 1, vector<int>(m + 1));int ans = 0;// i -> j 连边for (int i = 1; i <= n; ++i) {for (int j = 1; j <= m; ++j) {cin >> g[i][j];if (g[i][j]) {G.addEdge(i, n + j, 1, -1);++ans;} else {G.addEdge(i, n + j, 1, 1);}}}G.S = n + m + 1, G.T = G.S + 1;int suma = 0, sumb = 0;// S -> i 连边for (int i = 1; i <= n; ++i) {int x; cin >> x;G.addEdge(G.S, i, x, 0);suma += x;}// j -> T 连边for (int i = 1; i <= m; ++i) {int x; cin >> x;G.addEdge(n + i, G.T, x, 0);sumb += x;}//先特判 sum a != sum bif (suma != sumb) {cout << -1 << '\n';return;}G.work();//再特判 maxFlow != sum aif (G.MF != suma) {cout << -1 << '\n';return;}//答案就是 sum g[i][j] + minCostcout << ans + G.MC << '\n';
}signed main() {ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int t = 1; //cin >> t;while (t--) solve();return 0;
}
相关文章:
 E. Matrix Problem(费用流))
Educational Codeforces Round 160 (Rated for Div. 2) E. Matrix Problem(费用流)
原题链接:E. Matrix Problem 题目大意: 给出一个 n n n 行 m m m 列的 0 / 1 0/1 0/1 矩阵,再给出一些限制条件:一个长为 n n n 的数组 a a a,和一个长为 m m m 的数组 b b b 。 其中 a i a_{i} ai 表示第 …...
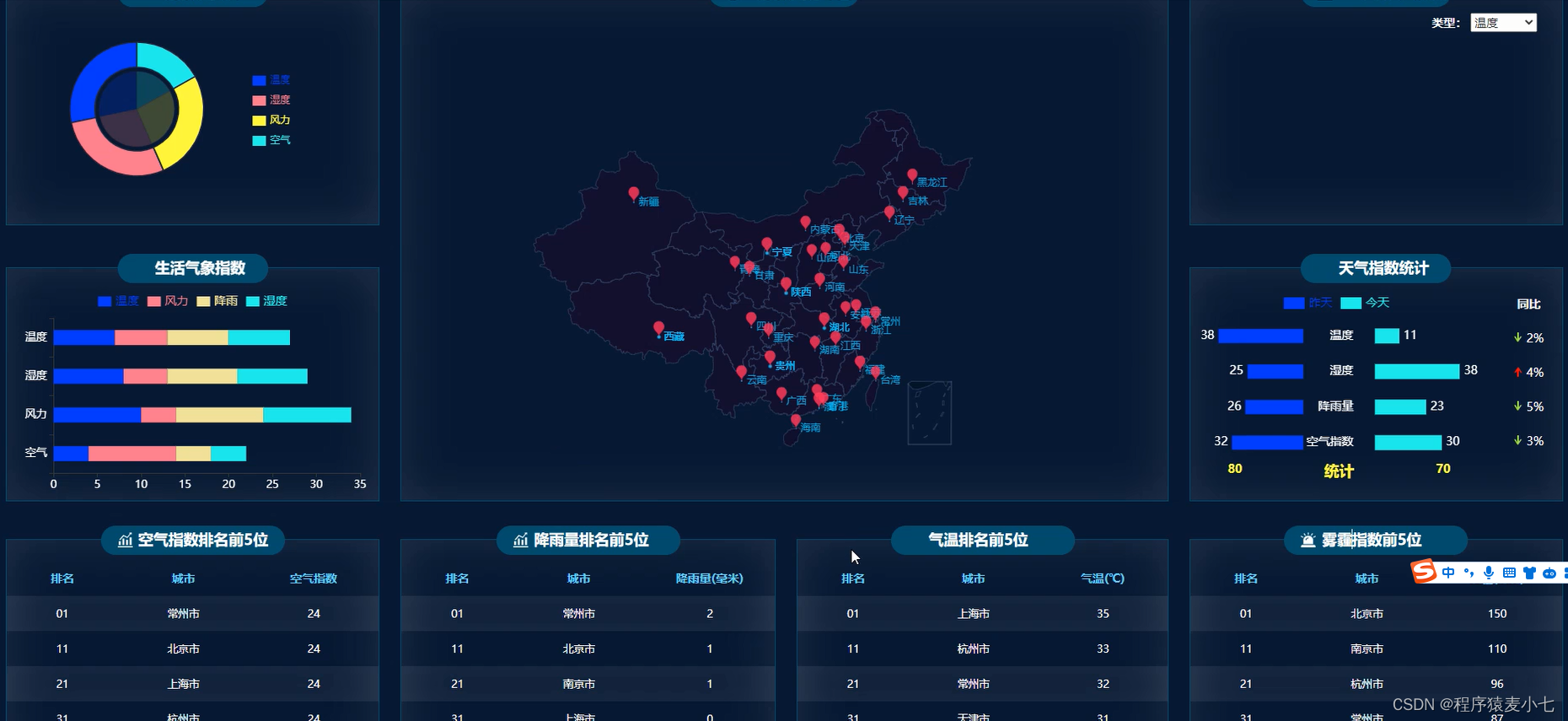
基于SpringBoot的气象数据监测分析大屏
项目描述 临近学期结束,还是毕业设计,你还在做java程序网络编程,期末作业,老师的作业要求觉得大了吗?不知道毕业设计该怎么办?网页功能的数量是否太多?没有合适的类型或系统?等等。这里根据疫情当下,你想解决的问…...

关于硅的制造芯片的过程
芯片是如何制作的? 先将硅融化制成硅晶片,再用光刻机印压电路。 bilibili芯片制作视频 硅晶片作为现代芯片的主要元件,广泛用于集成电路。 首先将多晶硅放入特制的密封炉,排除其中空气后加热到1420摄氏度,将融化的硅放…...

【深度学习笔记】3_10 多层感知机的PyTorch实现
注:本文为《动手学深度学习》开源内容,仅为个人学习记录,无抄袭搬运意图 3.10 多层感知机的简洁实现 下面我们使用PyTorch来实现上一节中的多层感知机。首先导入所需的包或模块。 import torch from torch import nn from torch.nn import …...

输入法在 Android13上候选词 候选区域 不显示的问题
背景 自研的输入法发现在 Android13 平台上不显示候选区域,在之前平台上以及需求是输入英文时不显示,中文需要显示。 最终解决办法:setExtractViewShown(false) Override public View onCreateCandidatesView() {...setExtractViewShown(f…...

Java 面向对象进阶 18 JDK8、9开始新增的方法;接口的应用;适配器设计模式;内部类(黑马)
一、JDK8开始新增的方法 默认方法不是抽象方法,所以不强制被重写: 但是如果被重写,就要去掉default关键字: public可以省略,但是default不可以省略: public是灰色的,代表可以省略 但是default是…...
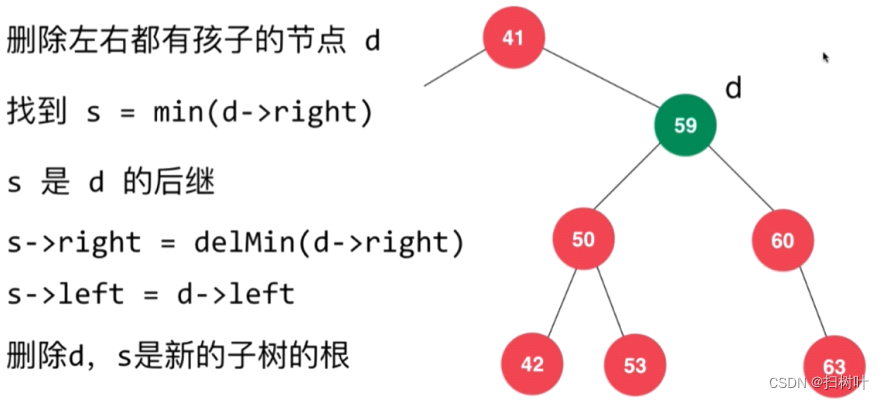
数据结构-二分搜索树(Binary Search Tree)
一,简单了解二分搜索树 树结构: 问题:为什么要创造这种数据结构 1,树结构本身是一种天然的组织结构,就好像我们的文件夹一样,一层一层的. 2,树结构可以更高效的处理问题 二,二分搜索树的基础 1、二叉树 2,二叉树的重要特性 满二叉树 总结: 1. 叶子结点出现在二叉树的最…...

YOLO如何训练自己的模型
目录 步骤 一、打标签 二、数据集 三、跑train代码出模型 四、跑detect代码出结果 五、详细操作 步骤 一、打标签 (1)在终端 pip install labelimg (2)在终端输入labelimg打开 如何打标签: 推荐文章…...
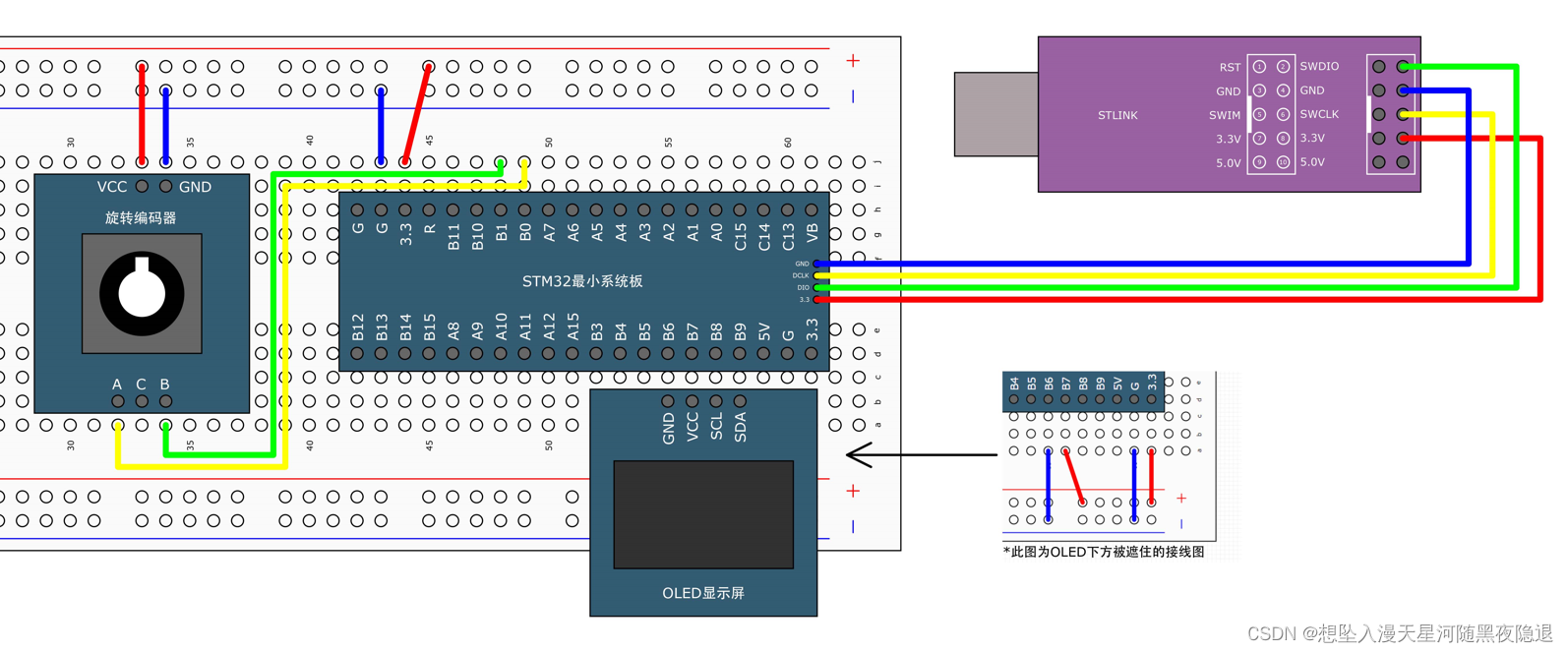
05 EXTI外部中断
一、中断系统 中断系统:管理和执行中断的逻辑结构。中断:在主程序运行过程中,出现了特定的中断触发条件——中断源,使得CPU暂停当前正在运行的程序,转而去处理中断程序,处理完成后又返回原来被暂停的位置继…...

2024.2.23
1.1.1 信号默认、捕获、忽略处理(普通信号) #include <myhead.h> void handler(int signo) {if(signoSIGINT){printf("用户键入 ctrlc\n");} } int main(int argc, const char *argv[]) {//忽略信号if(signal(SIGINT,SIG_IGN)SIG_ERR){perror("signal er…...

PHP实现分离金额和其他内容便于统计计算
得到的结果可以粘贴到excel计算 <?php if($_GET["x"] "cha"){ $tips isset($_POST[tips]) ? $_POST[tips] : ; $pattern /(\d\.\d|\d)/; $result preg_replace($pattern, "\t\${1}\t", $tips); echo "<h2><strong>数…...

基础数据结构和算法《》
递归 1.递归应该一种比较常见的实现一些特殊代码逻辑时需要做的,但常常也是最绕的一种方式,在解释递归 之前,我们用循环和递归来做个比较1.1.如果你打开一扇门后,同样发现前方也有一扇们,紧接着你又打开下一扇门...直…...
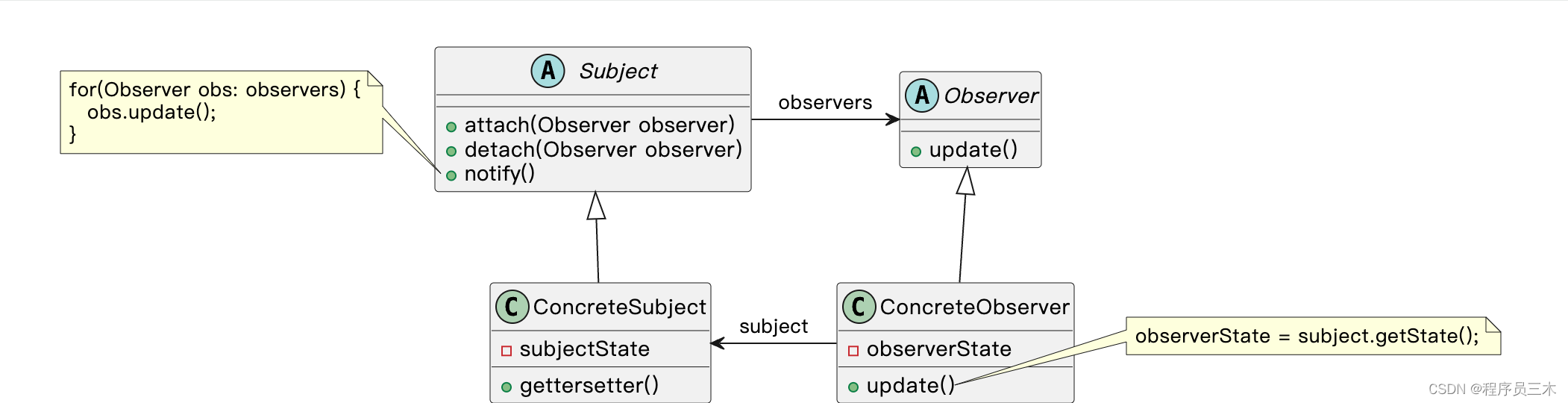
[设计模式Java实现附plantuml源码~行为型]对象间的联动~观察者模式
前言: 为什么之前写过Golang 版的设计模式,还在重新写Java 版? 答:因为对于我而言,当然也希望对正在学习的大伙有帮助。Java作为一门纯面向对象的语言,更适合用于学习设计模式。 为什么类图要附上uml 因为很…...
vue3+js 实现记住密码功能
常见的几种实现方式 1 基于spring security 的remember me 功能 localStorage 除非主动清除localStorage 里的信息 ,不然永远存在,关闭浏览器之后下次启动仍然存在 存放数据大小一般为5M 不与服务器进行交互通信 cookies 可以…...

基于单片机的太阳能电池板自动跟踪系统的研究
摘要 伴随着人类社会的发展,人口基数越来越大,电量消耗巨大,传统发电原 料污染环境的同时,可用量日益减少,给人类未来生产生活带来了一定的威胁, 因而解决日益剧增的用电量,寻求一种新能源显得极其重要。论文正是基于此 背景下,针对当前太阳能电池板采光率低、自动化水…...

React 模态框的设计(二)
自定义组件是每个前端开发者必备的技能。我们在使用现有框架时难免有一些超乎框架以处的特别的需求,比如关于弹窗,每个应用都会用到,但是有时我们使用的框架中提供的弹窗功能也是功能有限,无法满足我们的应用需求,今天…...

操作符详解3
✨✨ 欢迎大家来到莉莉的博文✨✨ 🎈🎈养成好习惯,先赞后看哦~🎈🎈 前面我们已经讲过算术操作符、赋值操作符、逻辑操作符、条件操作符和部分的单目操作 符,今天继续介绍一部分。 目录 1.操作符的分类 2…...

【C语言基础】:操作符详解(一)
文章目录 操作符详解1. 操作符的分类2. 二进制和进制转换2.1 什么是二进制、八进制、十进制、十六进制2.1.1 二进制和进制转换2.1.2 二进制转十进制2.2.3 二进制转八进制2.2.4 二进制转十六进制 3. 源码、反码、补码4. 移位操作符4.1 左移操作符4.2 右移操作符 5. 位操作符&…...
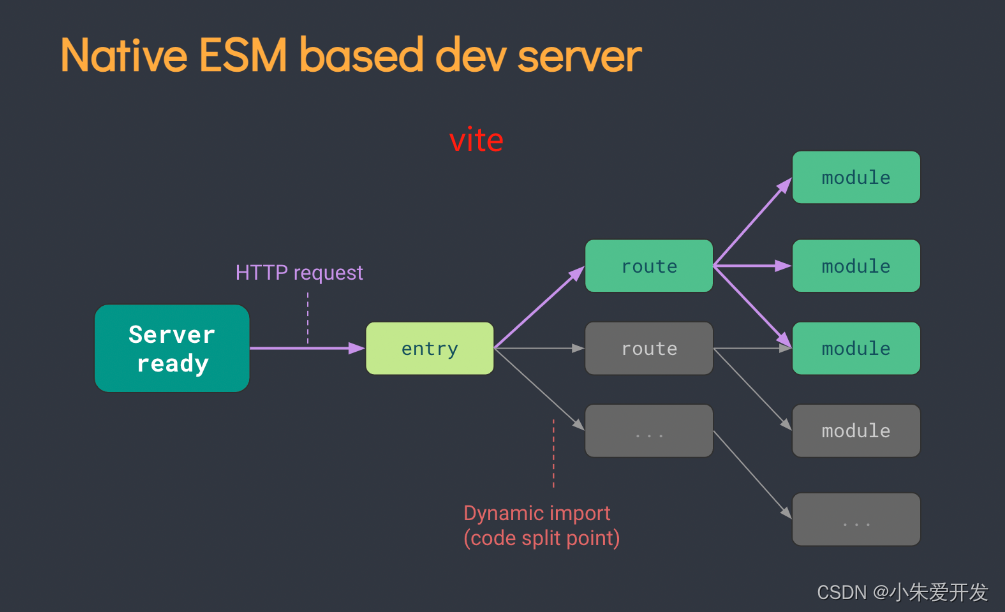
通俗易懂分析:Vite和Webpack的区别
1、对项目构建的理解 先从浏览器出发, 浏览器是由浏览器内核和JS引擎组成;浏览器内核编译解析html代码和css代码,js引擎编译解析JavaScript代码;所以从本质上,浏览器只能识别运行JavaScript、CSS、HTML代码。 而我们在…...

OpenCart程序结构与业务逻辑
一、程序业务逻辑说明 在 OpenCart 中,index.php 文件是整个应用程序的入口文件,它负责初始化应用程序并调度请求。以下是 index.php 文件加载执行的流程: 1. **设置路径常量:** - index.php 首先定义了一些重要的路径常量&…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
