pclpy 最小二乘法拟合平面
pclpy 最小二乘法拟合平面
- 一、算法原理
- 二、代码
- 三、结果
- 1.左边原点云、右边最小二乘法拟合平面后点云投影
- 四、相关数据
一、算法原理
平面方程的一般表达式为:
A x + B y + C z + D = 0 ( C ≠ 0 ) Ax + By + Cz + D = 0 \quad (C\neq0) Ax+By+Cz+D=0(C=0)
即:
Z = − A C x − B C y − D C Z = -\frac{A}{C}x-\frac{B}{C}y-\frac{D}{C} Z=−CAx−CBy−CD
记:
a 0 = − A C , a 1 = − B C , a 2 = − D C a_0 = -\frac{A}{C}, a_1 =-\frac{B}{C}, a_2=-\frac{D}{C} a0=−CA,a1=−CB,a2=−CD
所以:
Z = a 0 x + a 1 y + a 2 Z = a_0x + a_1y + a_2 Z=a0x+a1y+a2
要用该 n 个点拟合平面方程,即使:
∑ n = 1 N ( a 0 x + a 1 y + a 2 ) 2 − > m i n \sum_{n=1}^{N}{(a_0x + a_1y + a_2)^2}->min n=1∑N(a0x+a1y+a2)2−>min
要使S最小,对a,b,c求偏导
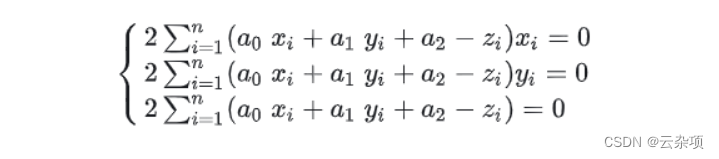
改写成矩阵的形式为:
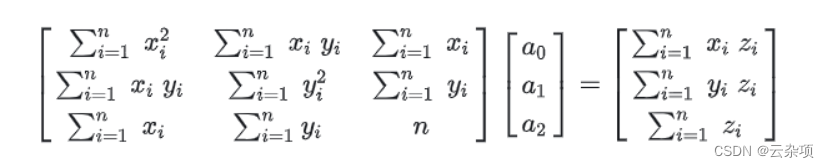
二、代码
from pclpy import pcl
import numpy as npdef CloudShow(cloud1, cloud2):"""Args:在一个窗口可视化多个点云cloud1: 点云数据1cloud2: 点云数据2"""viewer = pcl.visualization.PCLVisualizer("viewer") # 建立可刷窗口对象 窗口名 viewerv0 = 1 # 设置标签名(0, 1标记第一个窗口)viewer.createViewPort(0.0, 0.0, 0.5, 1.0, v0) # 创建一个可视化的窗口viewer.setBackgroundColor(0.0, 0.0, 0.0, v0) # 设置窗口背景为黑色single_color = pcl.visualization.PointCloudColorHandlerCustom.PointXYZ(cloud1, 255.0, 0, 0.0) # 将点云设置为红色viewer.addPointCloud(cloud1, # 要添加到窗口的点云数据。single_color, # 指定点云的颜色"sample cloud1", # 添加的点云命名v0) # 点云添加到的视图v1 = 2 # 设置标签名(2代表第二个窗口)viewer.createViewPort(0.5, 0.0, 1.0, 1.0, v1) # 创建一个可视化的窗口viewer.setBackgroundColor(255.0, 255.0, 255.0, v1) # 设置窗口背景为白色single_color = pcl.visualization.PointCloudColorHandlerCustom.PointXYZ(cloud2, 0.0, 255.0, 0.0) # 将点云设置为绿色viewer.addPointCloud(cloud2, # 要添加到窗口的点云数据。single_color, # 指定点云的颜色"sample cloud2", # 添加的点云命名v1) # 点云添加到的视图# 设置点云窗口(可移除对点云可视化没有影响)viewer.setPointCloudRenderingProperties(0, # 设置点云点的大小1, # 点云像素"sample cloud1", # 识别特定点云v0) # 在那个窗口可视化viewer.setPointCloudRenderingProperties(0, # 设置点云点的大小1, # 点云像素"sample cloud2", # 识别特定点云v1) # 在那个窗口可视化# viewer.addCoordinateSystem(1.0) # 设置坐标轴 坐标轴的长度为1.0# 窗口建立while not viewer.wasStopped():viewer.spinOnce(10)def plane(cloud, normal_vector):coeffs = pcl.ModelCoefficients() # 创建了一个模型系数对象coeffs.values.append(normal_vector[0]) # a = 0.0coeffs.values.append(normal_vector[1]) # b = 0.0coeffs.values.append(normal_vector[2]) # c = 1.0coeffs.values.append(normal_vector[3]) # d = 0.0# 创建滤波器proj = pcl.filters.ProjectInliers.PointXYZ() # 过滤器对象 proj,用于将点云投影到一个模型上。proj.setModelType(0) # 模型类型被设为 0,代表使用平面模型。proj.setInputCloud(cloud) # 将cloud点云数据进行处理proj.setModelCoefficients(coeffs) # 处理参数coeffscloud_projected = pcl.PointCloud.PointXYZ() # 建立保存点云proj.filter(cloud_projected) # 将投影结果保存return cloud_projectedif __name__ == '__main__':cloud1 = pcl.PointCloud.PointXYZ()reader = pcl.io.PCDReader() # 设置读取对象reader.read('res/bunny.pcd', cloud1) # 读取点云保存在cloud中# 调用函数,生成离散点x, y, z = cloud1.x, cloud1.y, cloud1.zN = cloud1.size()# ------------------------构建系数矩阵-----------------------------A = np.array([[sum(x ** 2), sum(x * y), sum(x)],[sum(x * y), sum(y ** 2), sum(y)],[sum(x), sum(y), N]])B = np.array([[sum(x * z), sum(y * z), sum(z)]])# 求解X = np.linalg.solve(A, B.T)print('平面拟合结果为:z = %.3f * x + %.3f * y + %.3f' % (X[0], X[1], X[2]))a, b, c, d = X[0], X[1], -1, X[2]plane_cloud = plane(cloud1, [a, b, c, d]) # 获得投影后的点云数据# ------------------ 可视化点云 -----------------CloudShow(cloud1, plane_cloud)
三、结果
1.左边原点云、右边最小二乘法拟合平面后点云投影
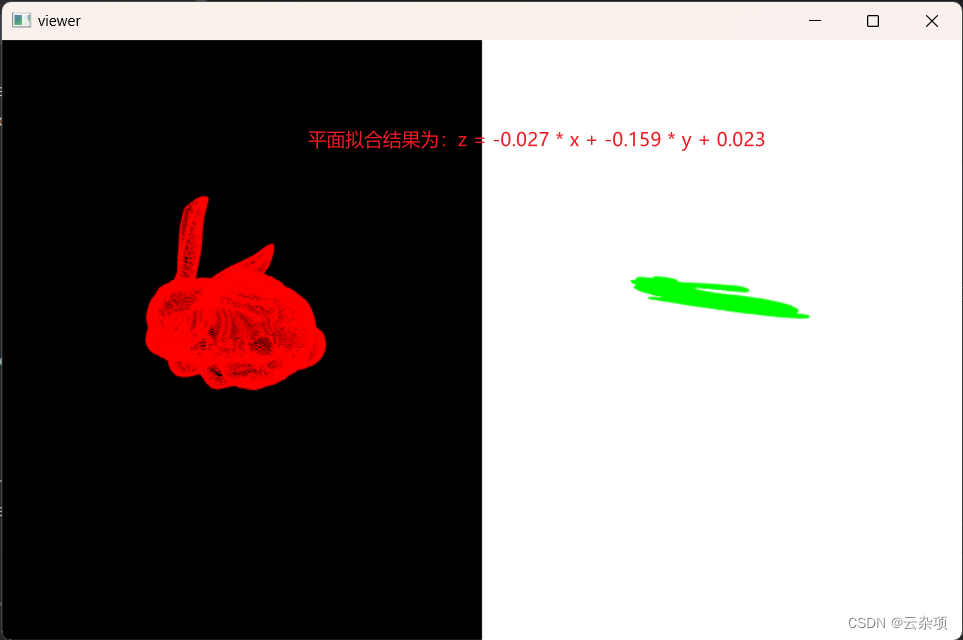
四、相关数据
最小二乘法拟合参考链接:最小二乘拟合平面(python/C++版) - 知乎 (zhihu.com)
相关文章:

pclpy 最小二乘法拟合平面
pclpy 最小二乘法拟合平面 一、算法原理二、代码三、结果1.左边原点云、右边最小二乘法拟合平面后点云投影 四、相关数据 一、算法原理 平面方程的一般表达式为: A x B y C z D 0 ( C ≠ 0 ) Ax By Cz D 0 \quad (C\neq0) AxByCzD0(C0) 即: …...

蓝桥杯备战刷题(自用)
1.被污染的支票 #include <iostream> #include <vector> #include <map> #include <algorithm> using namespace std; int main() {int n;cin>>n;vector<int>L;map<int,int>mp;bool ok0;int num;for(int i1;i<n;i){cin>>nu…...
Python习题详解
练习: 1,计算100以内奇数的和 #计算100以内所有奇数的和 sum 0 # n 1 # while n < 100: # # sum sum n # sum n # # n n 2 # n 2 # print(sum) n 99 #求偶数时n 100 while n > 0:sum n# n n - 2n - 2 print(sum)2,打印直…...
绩效考核利器:Excel报表模板,解锁企业高效员工评价新境界
一、背景与目标 在现今的企业管理中,绩效考核是一项至关重要的任务。它旨在评估员工的工作表现,激励员工积极进取,同时也是制定薪酬、晋升、培训等决策的重要依据。为了满足这一需求,我们设计了一款绩效考核Excel报表模板&#x…...

如何使用Lychee+cpolar搭建本地私人图床并实现远程访问存储图片
文章目录 1.前言2. Lychee网站搭建2.1. Lychee下载和安装2.2 Lychee网页测试2.3 cpolar的安装和注册 3.本地网页发布3.1 Cpolar云端设置3.2 Cpolar本地设置 4.公网访问测试5.结语 1.前言 图床作为图片集中存放的服务网站,可以看做是云存储的一部分,既可…...
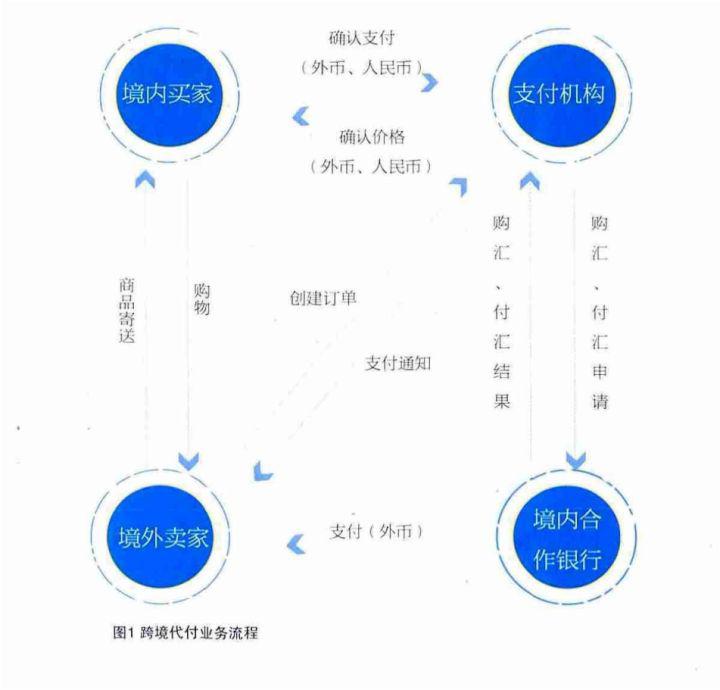
跨境支付介绍
1、跨境电商定义和分类; 2、国际贸易清结算; 3、跨境支付; 1、跨境电商定义和分类 跨境电商业务简单说就是指不同国家地域的主体通过电子商务进行交易的一种业务模式。同传统的电商不同,交易双方属于不同的国家。因此࿰…...
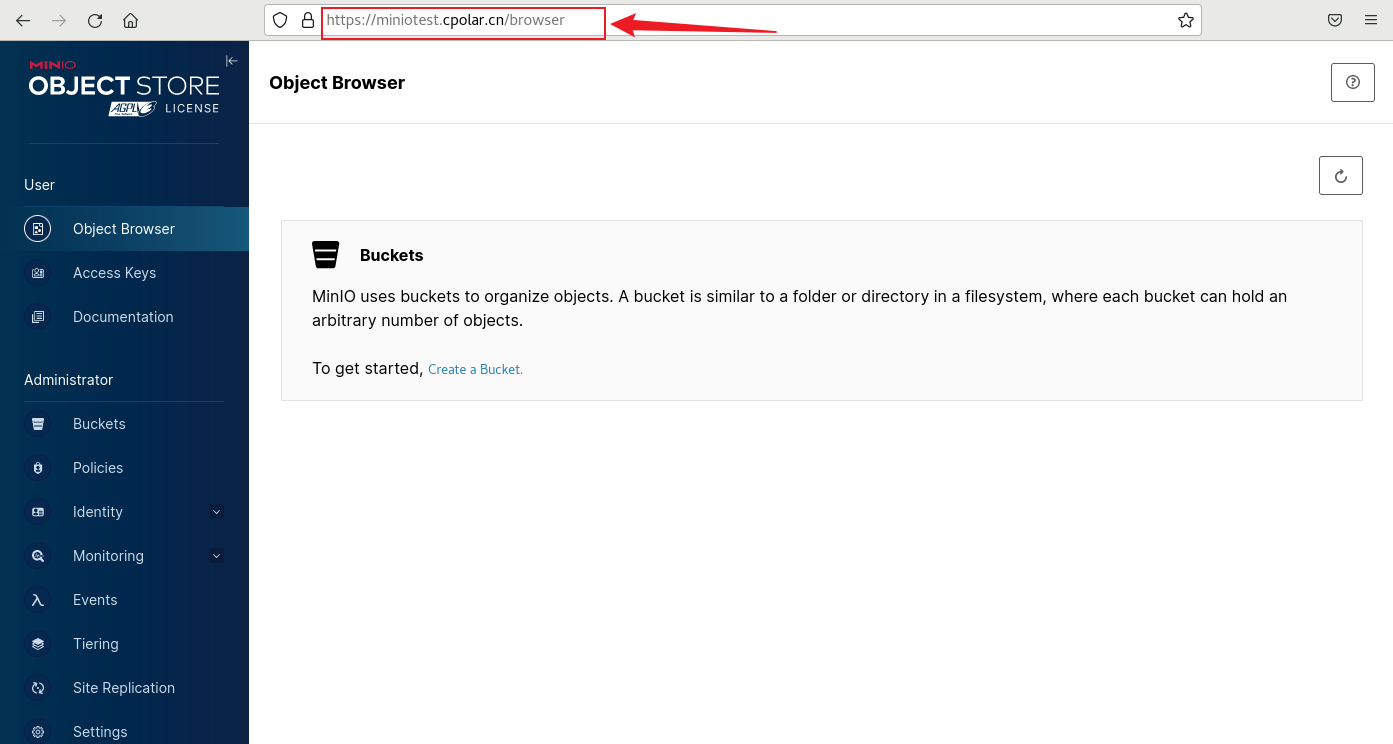
如何在Linux搭建MinIO服务并实现无公网ip远程访问内网管理界面
文章目录 前言1. Docker 部署MinIO2. 本地访问MinIO3. Linux安装Cpolar4. 配置MinIO公网地址5. 远程访问MinIO管理界面6. 固定MinIO公网地址 前言 MinIO是一个开源的对象存储服务器,可以在各种环境中运行,例如本地、Docker容器、Kubernetes集群等。它兼…...
Cortex-M可以跑Linux操作系统吗?
在开始前我有一些资料,是我根据网友给的问题精心整理了一份「Linux的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!! Cortex-M系列微控制器主要设计…...
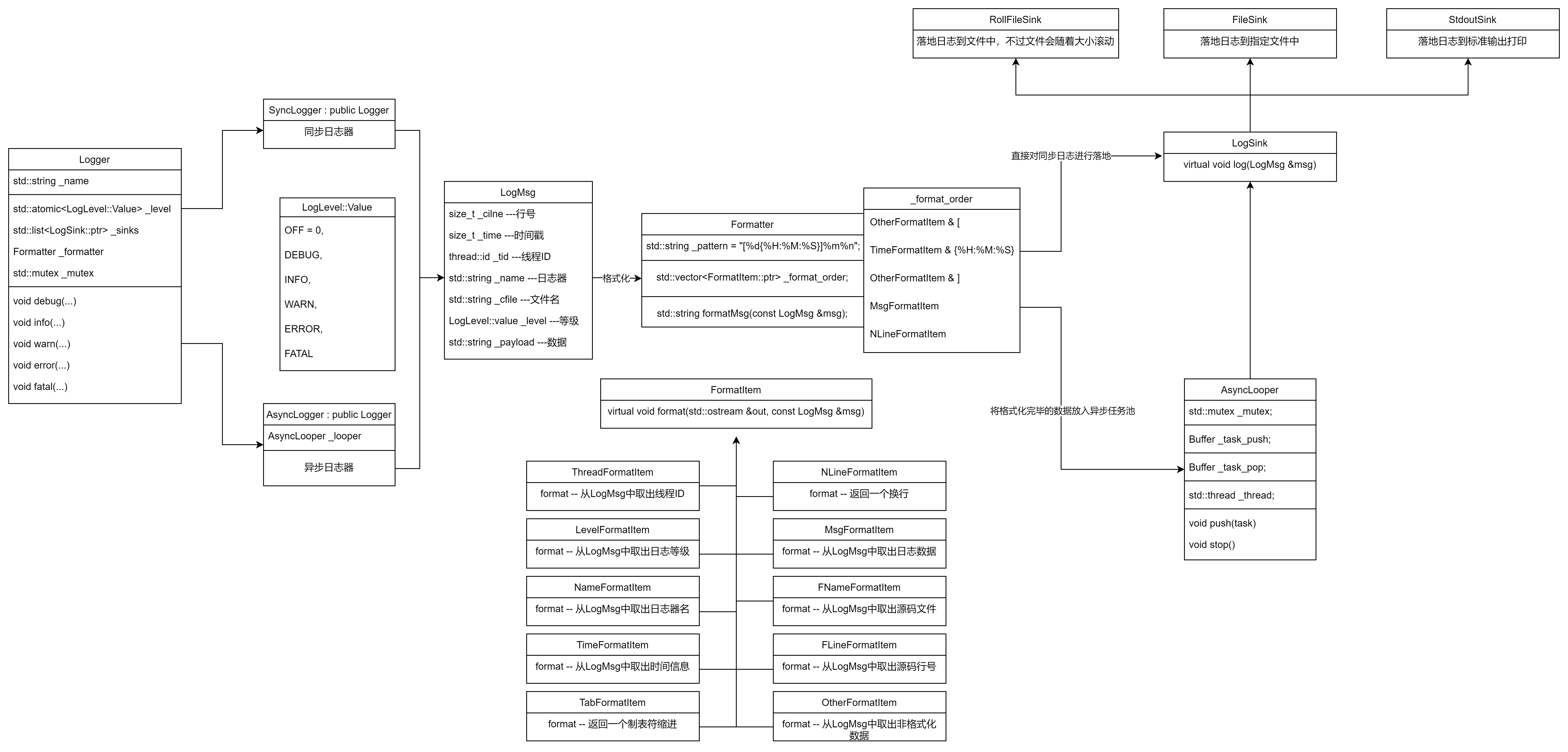
日志系统项目(2)项目实现(实用工具类、日志等级类、日志消息类、日志格式化输出类)
前面的文章中我们讲述了日志系统项目的前置知识点,再本文中我们将开始日志项目的细节实现。 日志系统框架设计 本项目实现的是一个多日志器日志系统,主要实现的功能是让程序员能够轻松的将程序运行日志信息落地到指定的位置,且支持同步与异…...

剑指offer面试题19 二叉树的镜像
考察点 树的遍历知识点 题目 分析 我们分析算法题目的思路基本上都是归纳法,即通过举一些普通的例子来推理出算法流程,而画图又是举例子的常用手段,比如针对树或者链表画画图,针对数字类的举一些数字的例子寻找规律,…...
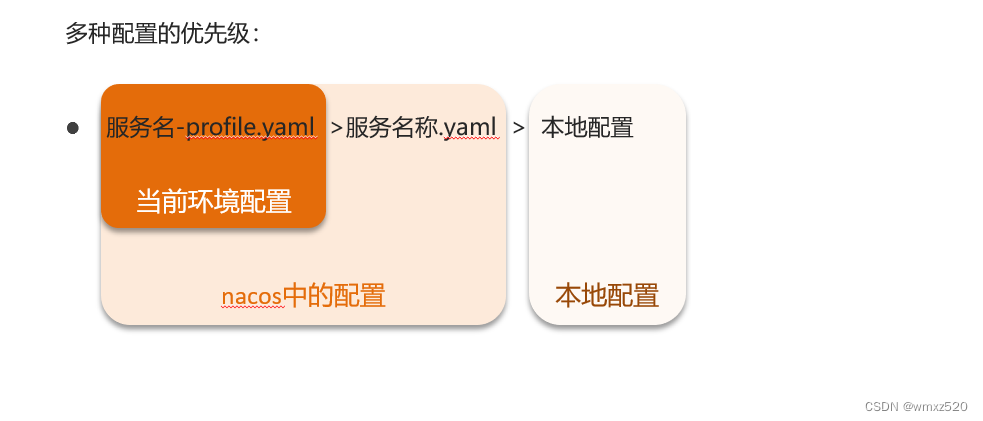
SpringCloud Alibaba 2022之Nacos学习
SpringCloud Alibaba 2022使用 SpringCloud Alibaba 2022需要Spring Boot 3.0以上的版本,同时JDK需要是17及以上的版本。具体的可以看官网的说明。 Spring Cloud Alibaba版本说明 环境搭建 这里搭建的是一个聚合项目。项目结构如下: 父项目的pom.xm…...

js之数组遍历
for 可以用来遍历数组、字符串、类数组、DOM节点,可以更改原数组,可以使用break、continue 跳出循环 return 只能在函数内部使用 for(声明循环变量;判断循环条件;更新循环变量){循环体 }forEach 参数(当前元素&#x…...

极狐GitLab 16.9 重磅发布,快来 pick 你心仪的功能吧~【五】
GitLab 是一个全球知名的一体化 DevOps 平台,很多人都通过私有化部署 GitLab 来进行源代码托管。极狐GitLab 是 GitLab 在中国的发行版,专门为中国程序员服务。可以一键式部署极狐GitLab。 沿袭我们的月度发版机制,今天我们正式发布极狐GitL…...
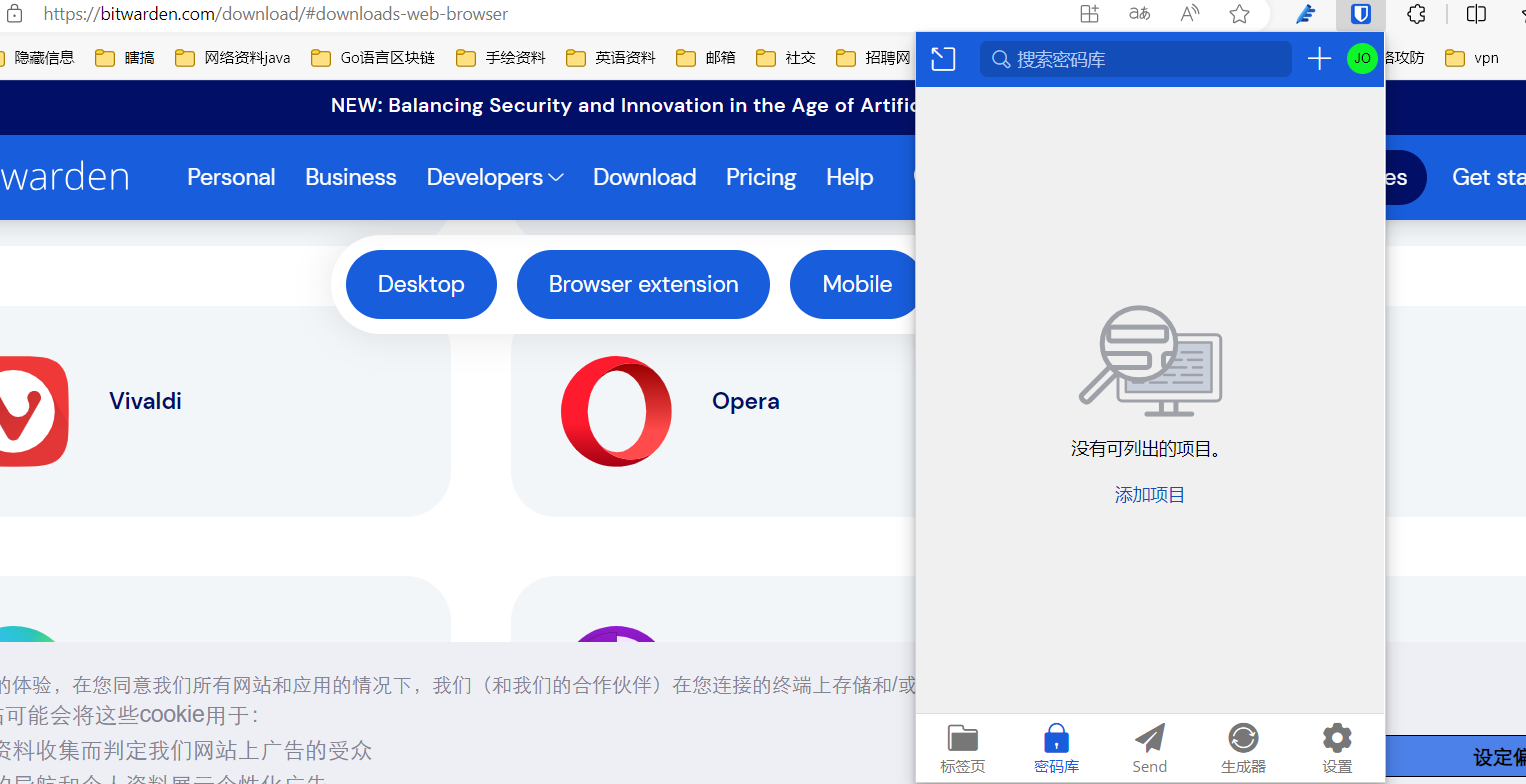
如何在本地部署密码管理软件bitwarden并结合cpolar实现远程同步
文章目录 1. 拉取Bitwarden镜像2. 运行Bitwarden镜像3. 本地访问4. 群晖安装Cpolar5. 配置公网地址6. 公网访问Bitwarden7. 固定公网地址8. 浏览器密码托管设置 Bitwarden是一个密码管理器应用程序,适用于在多个设备和浏览器之间同步密码。自建密码管理软件bitwarde…...
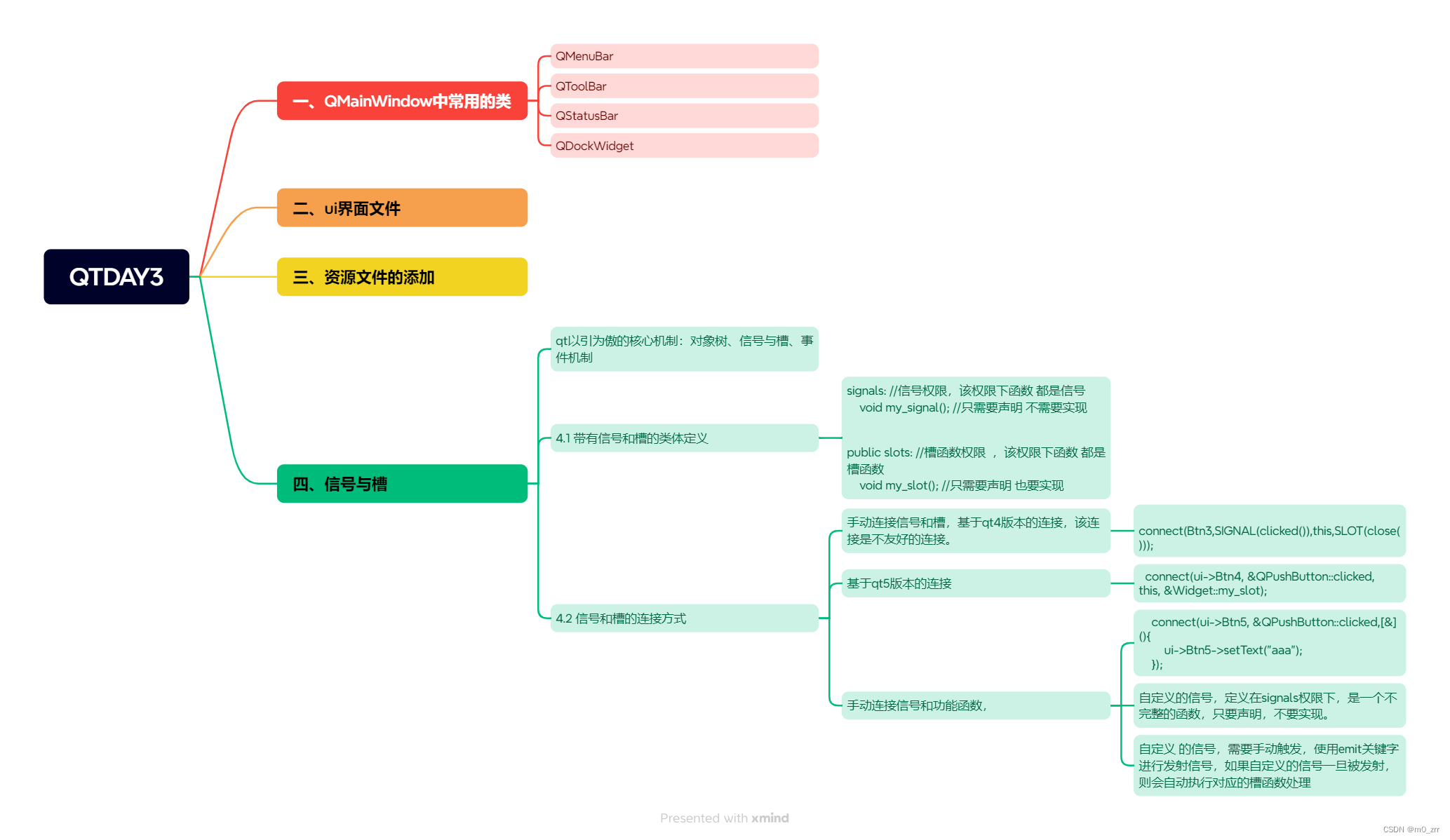
DT DAY3 信号和槽
作业: 1> 思维导图 2> 使用手动连接,将登录框中的取消按钮使用qt4版本的连接到自定义的槽函数中,在自定义的槽函数中调用关闭函数 btn3 new QPushButton("按钮3",this);btn3->resize(ui->btn2->width(),ui->b…...

Spring、SpringBoot、SpringCloud三者的区别
Spring、Spring Boot 和 Spring Cloud 是构建企业级 Java 应用程序的不同层次的框架和工具。下面详细介绍它们之间的区别: 1. Spring框架: 概述: Spring 是一个全功能的企业级 Java 框架,提供了依赖注入、面向切面编程、事务管理…...
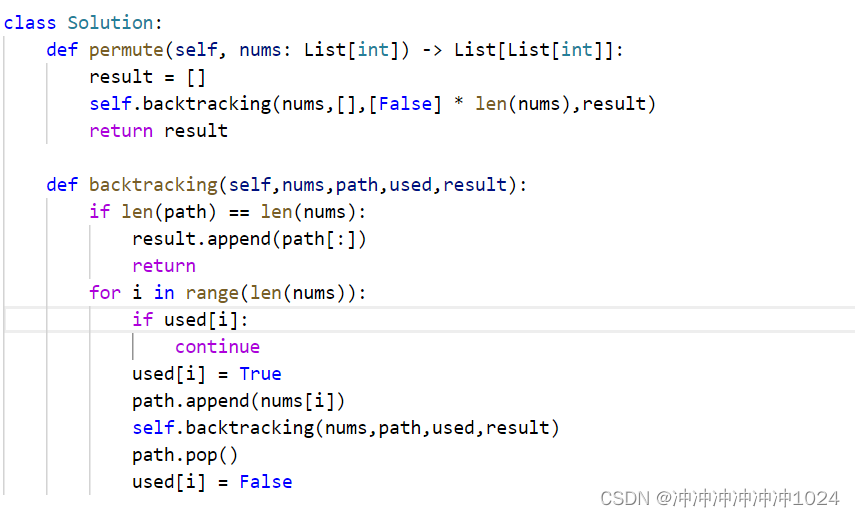
leetcode:46.全排列
1.什么是排列? 有顺序!! 2.树形结构: 使用used数组进行标记取过的元素,一个元素一个元素地进行取值,取完之后将used数组进行标记。 3.代码实现:(循环从i0开始,而不是…...

基于STM32的宠物箱温度湿度监控系统
基于STM32的宠物箱温度湿度监控系统 一、引言 随着人们生活水平的提高,养宠物已经成为越来越多人的选择。宠物作为家庭的一员,其生活环境和健康状况受到了广泛关注。温度和湿度是影响宠物舒适度和健康的重要因素之一。因此,开发一款能够实时监控宠物箱温度和湿度的系统具有…...

《高质量的C/C++编程规范》学习
目录 一、编程规范基础知识 1、头文件 2、程序的板式风格 3、命名规则 二、表达式和基本语句 1、运算符的优先级 2、复合表达式 3、if语句 4、循环语句的效率 5、for循环语句 6、switch语句 三、常量 1、#define和const比较 2、常量定义规则 四、函数设计 1、参…...
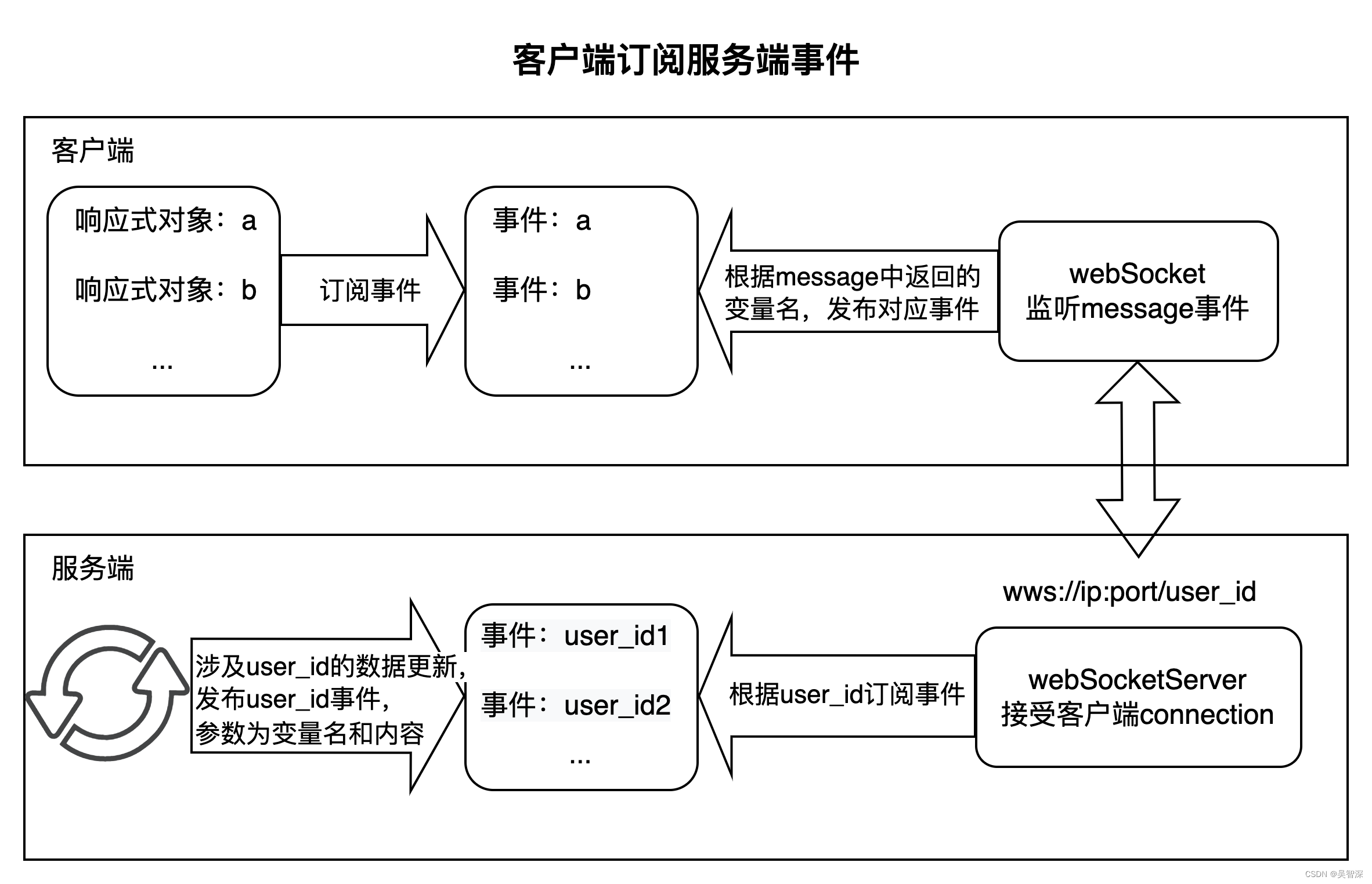
客户端订阅服务端事件的机制
一、场景描述 产业大脑平台是一个典型的审核系统,用户发布到平台的信息需要经过审核员审核后生效。 用户发布信息->审核员审核信息->用户信息生效,这一流程可能发生在用户的同一次登录周期内。为了使客户端能实时响应信息的状态变化,…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...
