字符串hash
K - 子串翻转回文串
2020ccpc河南省赛
字符串哈希:将字符串变成x进制数
对公式的理解:
举个十进制数的例子:123456
h[1]=1;
h[2]=1*10+2=12;
h[3]=12*10+3=123;
h[4]=123*10+4=1234;
.........
h[i]=h[i-1]*x+a[i];
h[i]代表的恰巧是整个数的前缀
用p[i]表示进制数的 i 次方;
想要单取出3-5的子串的值345
步骤;
1,先取出前缀12345(q[5])
2,再减去12000:(h[2]*1000);
取子串哈希值的公式为:h[r]-h[l-1] *(r-l+1);
本题思路:
去掉前缀后缀相同的部分,剩余的前缀或后缀必定要翻转一次
判法:正反跑一次哈希(下标不变权值翻转)
--------------------------------------> 正向权值整串s1
----------> 正向权值翻转部分s2
<---------- 反向权值翻转部分s3
<-------------------------------------- 正向权值整串s4
判法:比较翻转前与翻转后的整串的哈希制是否一样
long long get1(int l,int r)
{
if(l==0) return h1[r];
return ((h1[r]%mod-h1[l-1]*p[r-l+1]%mod)+mod)%mod;/*注意负数取模*/
}
求正向的字符串的hash值
long long get2(int l,int r)
{
return (h2[l]%mod-h2[r+1]*p[r-l+1]%mod+mod)%mod;
}
求反向的字符串的hash值
反向之后如12345中的5是最高位,如求1-3的话我们就应该让a[1]-a[4]*10的(r-l+1)次方
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define YES cout<<"YES"<<endl
#define NO cout<<"NO"<<endl
typedef long long ll;
typedef pair<int,int> PII;
const ll mod=1e9+7;
const int INF=0x3f3f3f3f;
const int N = 5e5+10;
int st[N];int ed[N];int p[N];
int base=131;
#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
int get1(int l,int r)
{return (st[r]-st[l-1]*p[r-l+1]%mod+mod)%mod;
}
int get2(int l,int r)
{return (ed[l]-ed[r+1]*p[r-l+1]%mod+mod)%mod;
}
bool check(int l,int r,int len)
{int dex = (st[len] - get1(l, r) * p[len - r] % mod + get2(l, r) * p[len - r] % mod + mod) % mod;/*从s1中取出s2放入s3所得出整串的哈希值*/int dey = (ed[1] - get2(l, r) * p[l - 1] % mod + get1(l, r) * p[l - 1] % mod + mod) % mod;/*从s4中取出s3放入s2所得出整串的哈希值*/ return dex == dey;
}
void solve()
{string s;cin>>s;int len=s.size();s=" "+s;int f=1;for(int i=1;i<=len/2;i++){if(s[i]!=s[len-i+1]){f=0;break;}} if(f==1){cout<<"Yes"<<endl;return ;}else{int pos;for(int i=1;i<=len;i++){if(s[i]!=s[len-i+1]){pos=i;break;}}p[0]=1;for(int i=1;i<=len;i++){st[i]=(st[i-1]*base%mod+s[i])%mod; p[i]=p[i-1]*base%mod;}ed[len+1]=0;for(int j=len;j>=1;j--){ed[j]=(ed[j+1]*base%mod+s[j])%mod;}for(int i=pos;i<=len-pos+1;i++){int l=pos,r=i;int ll=i,rr=len-pos+1;if(check(l,r,len)||check(ll,rr,len)){cout<<"Yes"<<endl;return ;} } }cout<<"No"<<endl;
}
signed main()
{ios;int t;cin>>t;while(t--){solve();}
}相关文章:

字符串hash
K - 子串翻转回文串2020ccpc河南省赛字符串哈希:将字符串变成x进制数对公式的理解:举个十进制数的例子:123456h[1]1;h[2]1*10212;h[3]12*103123;h[4]123*1041234;.........h[i]h[i-1]*xa[i];h[i]代表的恰巧是整个数的前缀用p[i]表…...

试题 算法训练 转圈游戏
问题描述 n个小伙伴(编号从0到n-1)围坐一圈玩游戏。按照顺时针方向给n个位置编号,从0到n-1。 最初,第0号小伙伴在第0号位置,第1号小伙伴在第 1 号位置,……,依此类推。 游戏规则如下&am…...

【uni-app教程】九、运行环境判断与跨端兼容
(1)开发环境和生产环境 uni-app 可通过 process.env.NODE_ENV 判断当前环境是开发环境还是生产环境,一般用于连接测试服务器或生产服务器的动态切换。 在HBuilderX 中,点击「运行」编译出来的代码是开发环境,点击「发行…...

扩展WSL2虚拟硬盘的大小
扩展WSL2虚拟硬盘的大小 1、在 Windows PowerShell 中终止所有 WSL 实例 wsl --shutdown2、查看 WSL 实例运行状态,确认关闭,并记住发行版的名称 wsl -l -v如果没有更改移动过发行版安装包位置,那么可以通过以下方法查找到发行版的安装包位…...

Win系统蓝牙设备频繁卡顿/断连 - 解决方案
Win系统蓝牙设备频繁卡顿/断连 - 解决方案前言常见网卡Intel无线网卡(推荐)Realtek无线网卡总结查看本机网卡解决方案更新驱动更换网卡(推荐)前言 无线网卡有2个模块,一个是WiFi,一个是蓝牙,因…...
Git学习入门(2)- 基本命令操作总结
个人博客:我的个人博客,各位大佬来玩1 创建 git仓库1.1 从现有工作目录中初始化新仓库需要到你需要用git管理的项目中输入以下命令:git init便会创建一个空的git项目,并且当前目录下会出现一个名为 .git 的目录, Git 需…...

SPringCloud:Nacos快速入门及相关属性配置
目录 一、Nacos快速入门 1、在父工程中添加spring-cloud-alilbaba的管理依赖 2、如果有使用eureka依赖,将其注释 3、添加nacos的客户端依赖 4、修改yml文件,注释eureka配置 5、启动测试 二、Nacos相关属性配置 1、Nacos服务分级存储 2、根据集群…...

医疗器械之模糊算法(嵌入式部分)
模糊控制 所谓模糊控制,就是对难以用已有规律描述的复杂系统,采用自然语言(如大,中,小)加以描述,借助定性的,不精确的以及模糊的条件语句来表达,模糊控制是一种基于语言的…...
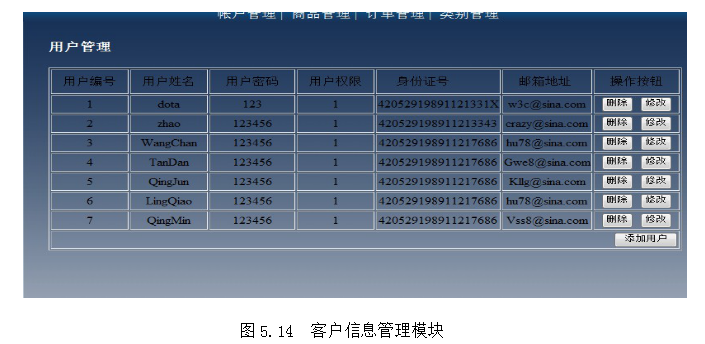
网上销售笔记本系统
技术:Java、JSP等摘要:本文讲述了基于B/S模式的笔记本电脑在线销售系统的设计与实现。所谓的笔记本电脑在线销售系统是通过网站推广互联企业的笔记本电脑和技术服务,并使客户随时可以了解企业和企业的产品,为客户提供在线服务和订…...
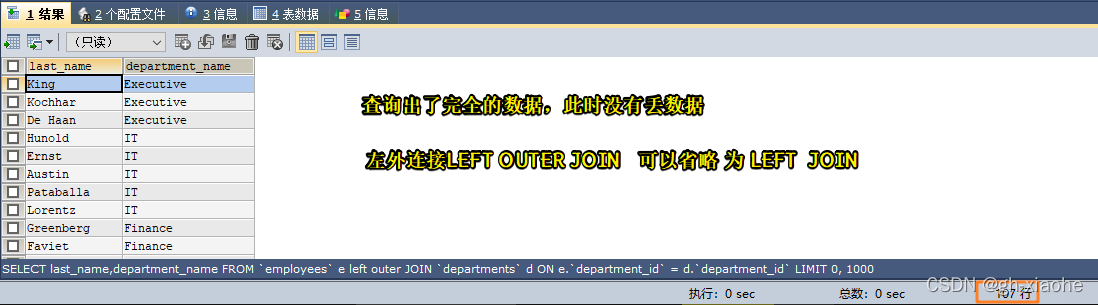
MySQL基础查询操作
文章目录🚏 Select语句🚀 一、SQL底层执行原理🚬 (一)、查询的结构🚬 (二)、SQL语句的执行过程🚭 1、WHERE 为什么不包含聚合函数的过滤条件?(面试…...

English Learning - L2 语音作业打卡 小元音 [ʌ] [ɒ] Day9 2023.3.1 周三
English Learning - L2 语音作业打卡 小元音 [ʌ] [ɒ] Day9 2023.3.1 周三💌发音小贴士:💌当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音 [ʌ]&…...
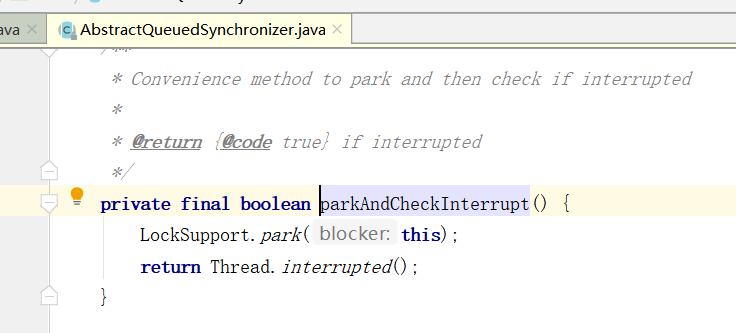
Condition 源码解读
一、Condition 在并发情况下进行线程间的协调,如果是使用的 synchronized 锁,我们可以使用 wait/notify 进行唤醒,如果是使用的 Lock 锁的方式,则可以使用 Condition 进行针对性的阻塞和唤醒,相较于 wait/notify 使用…...
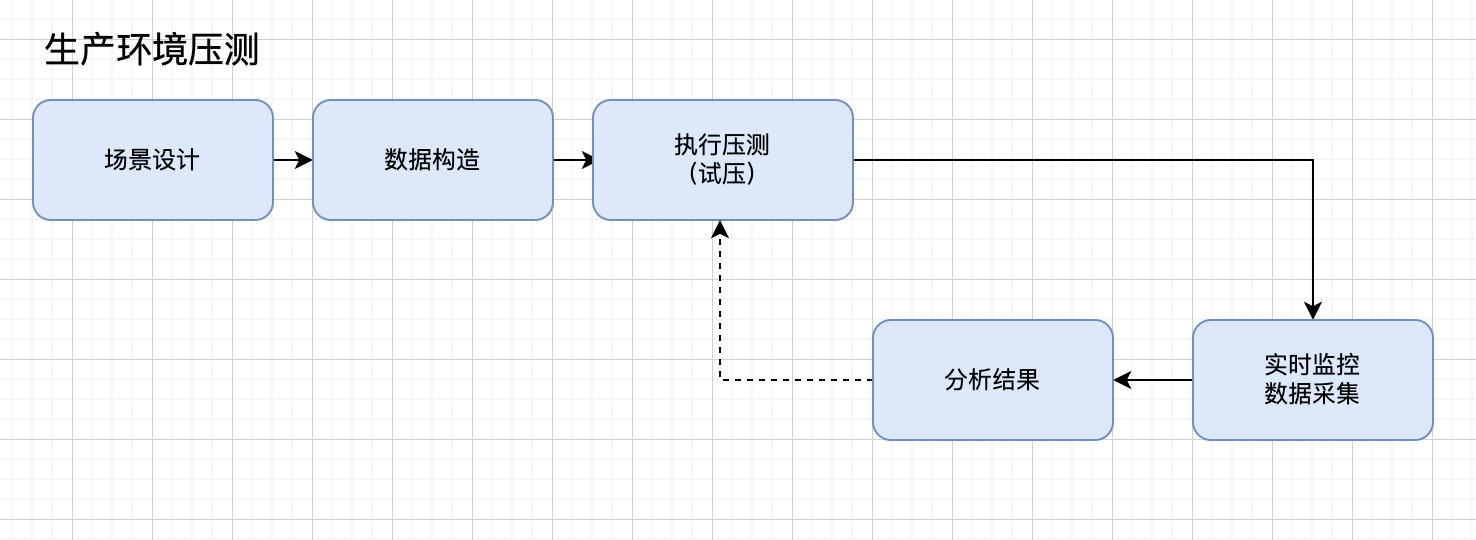
看完这篇入门性能测试
大家好,我是洋子。最近组内在进行服务端高并发接口的性能压测工作,起因是2023年2月2日,针对胡某宇事件进行新闻发布会直播,几十万人同时进入某媒体直播间,造成流量激增 从监控上可以看出,QPS到达某峰值后&…...

推导部分和——带权并查集
题解: 带权并查集 引言: 带权并查集是一种进阶的并查集,通常,结点i的权值等于结点i到根节点的距离,对于带权并查集,有两种操作需要掌握——Merge与Find,涉及到路径压缩与维护权值等技巧。 带…...
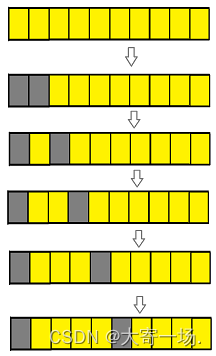
费解的开关/翻硬币
🌱博客主页:大寄一场. 🌱系列专栏: 算法 😘博客制作不易欢迎各位👍点赞⭐收藏➕关注 题目:费解的开关 你玩过“拉灯”游戏吗? 25盏灯排成一个 55 的方形。 每一个灯都有一个开关&…...
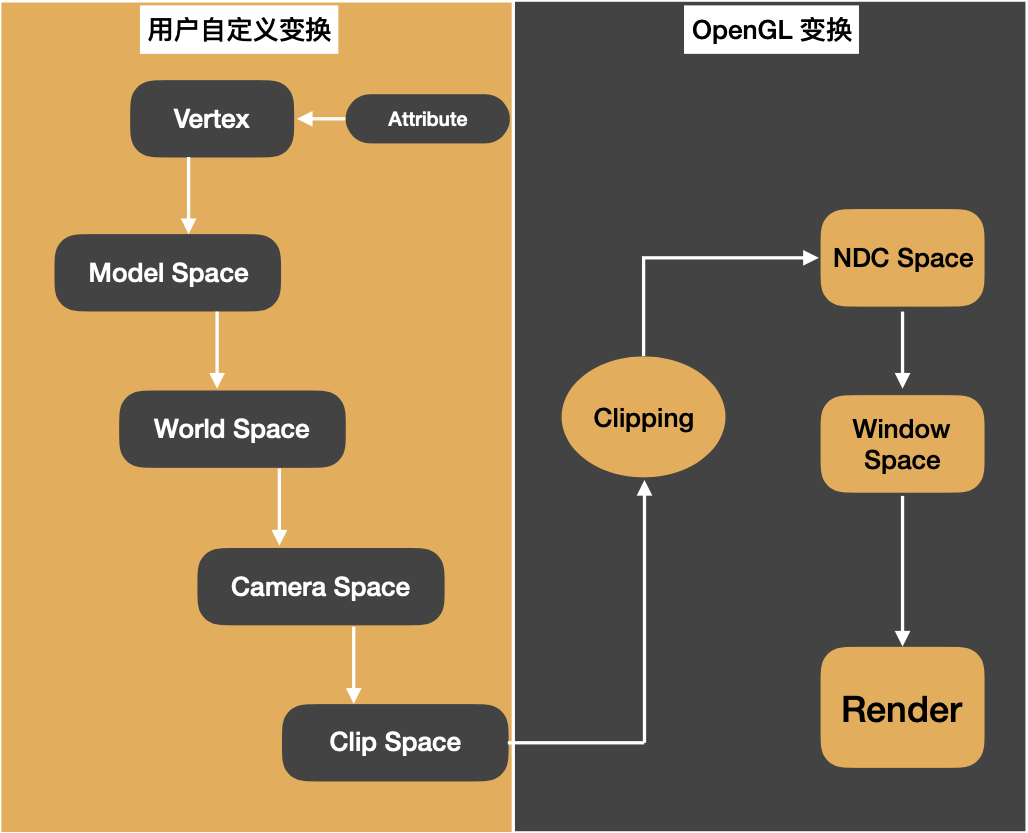
OpenGL中的坐标系
1、2D笛卡尔坐标系2D笛卡尔坐标系跟我们高中的时候学习的坐标系一样,是由x、y决定的。2、3D笛卡尔坐标系3D笛卡尔坐标系坐标由x、y、z决定,满足右手定则。3、视口glViewport(GLint x,GLint y,GLsizei width,GLsizei height)窗口和视口大小可以相同&#…...

Spring——Spring介绍和IOC相关概念
Spring是以Spring Framework为核心,其余的例如Spring MVC, Spring Cloud,Spring Data,Spring Security SpringBoot的基础都是Spring Framework。 Spring Boot可以在简化开发的基础上加速开发。 Spring Cloud分布式开发 Spring有…...

A+B Problem
AB Problem 题目描述 输入两个整数 a,ba, ba,b,输出它们的和(∣a∣,∣b∣≤109|a|,|b| \le {10}^9∣a∣,∣b∣≤109)。 注意 Pascal 使用 integer 会爆掉哦!有负数哦!C/C 的 main 函数必须是 int 类型,…...
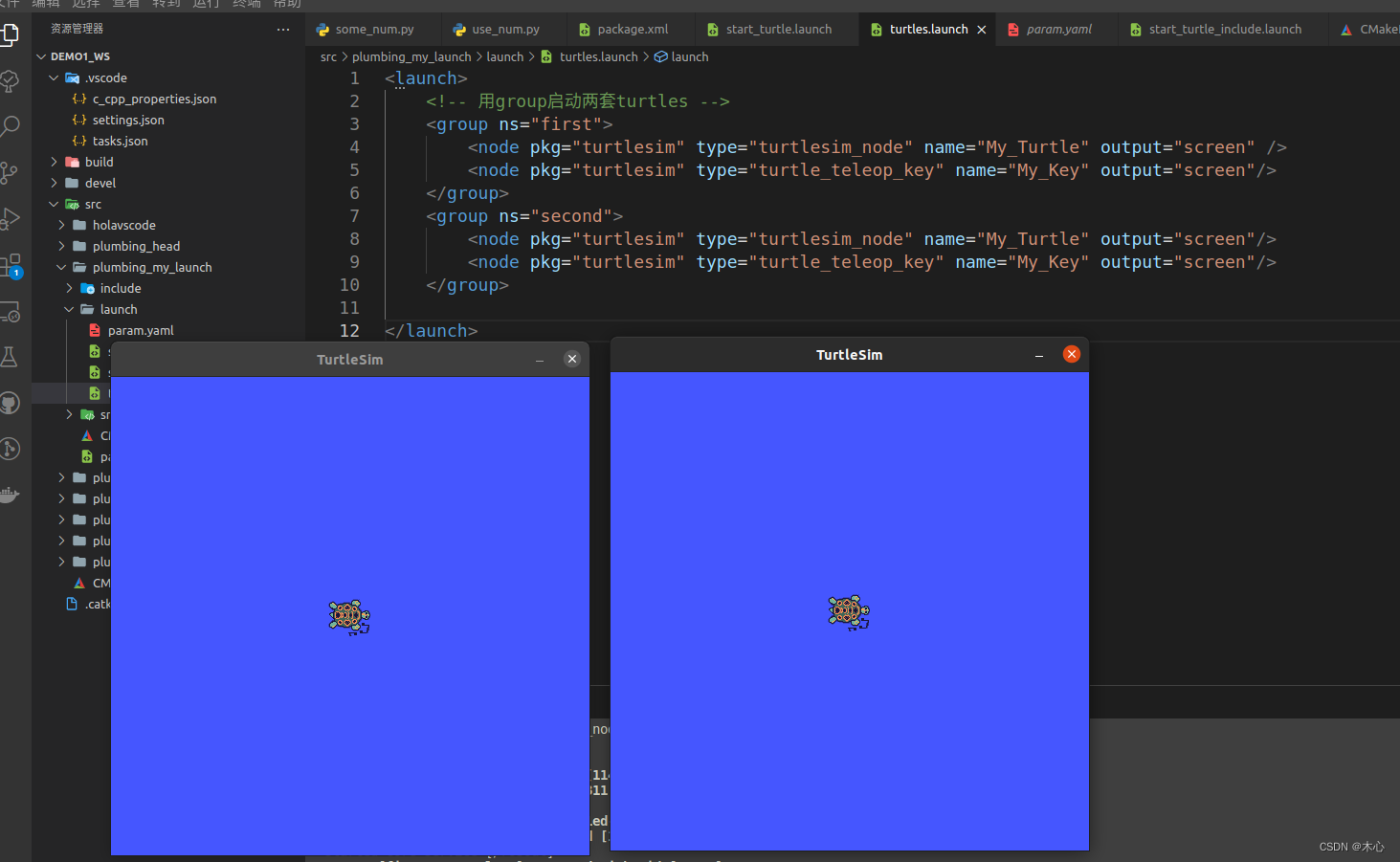
【ROS学习笔记11】ROS元功能包与launch文件的使用
【ROS学习笔记11】ROS元功能包与launch文件的使用 文章目录【ROS学习笔记11】ROS元功能包与launch文件的使用前言一、ROS元功能包二、ROS节点运行管理launch文件2.1 launch文件标签之launch2.2 launch文件标签之node2.3 launch文件标签之include2.4 launch文件标签之remap2.5 l…...

【python】
print函数 同时输出多行变量 print(a, b, sep\n) (23条消息) python3 中print函数参数详解,print(*values, sep , end\n, filesys.stdout, flushFalse)中参数介绍_sep,_phantom-dapeng的博客-CSDN博客 input() 输入浮点数,不能用int(input()) int()…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...
