2023牛客寒假算法集训营4
目录
- A. [清楚姐姐学信息论](https://ac.nowcoder.com/acm/contest/46812/A)(数学)
- B. [清楚姐姐学构造](https://ac.nowcoder.com/acm/contest/46812/B)(数学 + 构造)
- C. [清楚姐姐学01背包(Easy Version)](https://ac.nowcoder.com/acm/contest/46812/C)(01背包)
- D. [清楚姐姐学01背包(Hard Version)](https://ac.nowcoder.com/acm/contest/46812/D)(01背包)
- E. [清楚姐姐打怪升级](https://ac.nowcoder.com/acm/contest/46812/E)(数学 or 二分)
- F. [清楚姐姐学树状数组](https://ac.nowcoder.com/acm/contest/46812/F)(二叉树 + DFS)
- G. [清楚姐姐逛街(Easy Version)](https://ac.nowcoder.com/acm/contest/46812/G)(BFS)
- L. [清楚姐姐的三角形I](https://ac.nowcoder.com/acm/contest/46812/L)(数学 + 推公式)
- M. [清楚姐姐的三角形II](https://ac.nowcoder.com/acm/contest/46812/M)(构造)
A. 清楚姐姐学信息论(数学)
题意:
给定两个非负整数 xxx , yyy (2≤x,y≤109)(2 \le x, y \le 10^9)(2≤x,y≤109) ,表示 xxx 进制和 yyy 进制,比较哪种进制的信息表示效率更高。
当且仅当,xxx 进制和 yyy 进制分别使用 x⋅yx \cdot yx⋅y 个数时, xxx 进制能够表示的数字数目大于 yyy 进制,则称 xxx 进制的信息表示效率大于 yyy 进制。
思路一:
比较 xyx^yxy 和 yxy^xyx 的大小就行。
但是你这样写会发现,炸了,数据太大了,所以需要优化一下:
改成比较 y⋅logxy·log_xy⋅logx 和 x⋅logyx·log_yx⋅logy 就行了。
特别注意:优化后要用浮点数去比较,存在精度问题,如果用整数比较会有部分测试点过不了。
代码:
#include <bits/stdc++.h>
#define ll long long
#define endl '\n'
using namespace std;int main()
{ll x, y;cin >> x >> y;if (x == y) cout << x << endl;else {double xx = y * log(x);double yy = x * log(y);if (xx > yy) cout << x << endl;else if (xx < yy) cout << y << endl;else cout << min(x, y) << endl;}return 0;
}
思路二:
思路二就比较神奇,用的是数学的方法。
结论:eee 进制是效率最高的进制。
因此越靠近 eee 进制效率越高,e≈2.7e ≈ 2.7e≈2.7 ,所以在比较 (2,3)(2, 3)(2,3) 时,333 进制效率更高,其他情况都是小的进制更优。
代码:
#include <bits/stdc++.h>
#define ll long long
#define endl '\n'
using namespace std;int main()
{ll x, y;cin >> x >> y;if (x == 2 || y == 3) cout << 3 << endl;else cout << min(x, y) << endl;return 0;
}
B. 清楚姐姐学构造(数学 + 构造)
题意:
给定一个长度为 NNN 的数组 ccc 和一个质数 mmm,请你构造另外两个 同余等式 数组 a,ba,ba,b 满足:
{ai≡aN−1−i(modm)bi≡−bN−1−i(modm)ci≡ai+bi(modm)\left\{\begin{matrix} a_{i}\equiv a_{N-1-i}\pmod{m} \\ b_{i}\equiv -b_{N-1-i}\pmod{m} \\ c_{i}\equiv a_{i}+b_{i}\pmod{m} \end{matrix}\right.⎩⎨⎧ai≡aN−1−i(modm)bi≡−bN−1−i(modm)ci≡ai+bi(modm)
数组 a,b,ca,b,ca,b,c 的下标均从 000 开始计算。
如果可以构造出数组 a,ba,ba,b,则首先输出 YesYesYes,然后输出任意一种解,否则只需输出一行一个字符串 NoNoNo 。
≡\equiv≡ 为同余符号,它表示两个整数对 mmm 取余数的结果相同,对于负数取余数,若结果仍为负数,则需要加上 mmm 。
思路:
一个重要结论:任何一个函数都可以表示成奇函数和偶函数的和。
aaa 数组就是两边的数关于中心对称轴相等,而 bbb 数组则是关于中心对称轴相反。
要求 ci=ai+bic_i = a_i + b_ici=ai+bi ,即要求构造一个奇函数和一个偶函数来表示任意一个函数。
出题人题解
任取一个数列 ccc,设 c[i]≡a[i]+b[i]c[i]\equiv a[i]+b[i]c[i]≡a[i]+b[i] ,设 a[i]a[i]a[i] 数列关于 N/2N/2N/2 对称, b[i]b[i]b[i] 数列关于 N/2N/2N/2 对称相反。
则 c[N−i−1]≡a[N−i−1]+b[N−i−1]c[N-i-1]\equiv a[N-i-1]+b[N-i-1]c[N−i−1]≡a[N−i−1]+b[N−i−1] .
两式相加可得 c[i]+c[N−i−1]≡a[i]+b[i]+a[N−i−1]+b[N−i−1]c[i]+c[N-i-1] \equiv a[i]+b[i]+ a[N-i-1]+b[N-i-1]c[i]+c[N−i−1]≡a[i]+b[i]+a[N−i−1]+b[N−i−1] ,根据题意, b[i]b[i]b[i] 数列对称相反消掉, a[i]a[i]a[i] 数列关于 N/2N/2N/2 对称则 a[i]≡a[N−i−1]a[i] \equiv a[N-i-1]a[i]≡a[N−i−1] 。化简得
c[i]+c[N−i−1]≡2⋅a[i]c[i]+c[N-i-1] \equiv 2\cdot a[i]c[i]+c[N−i−1]≡2⋅a[i] 即 a[i]≡(c[i]+c[N−i−1])⋅inv(2)a[i] \equiv (c[i]+c[N-i-1])\cdot inv(2)a[i]≡(c[i]+c[N−i−1])⋅inv(2) 。注意当 m=2m=2m=2 无逆元需要特殊处理。
相似的,两式相减得 b[i]≡(c[i]−c[N−i−1])⋅inv(2)b[i] \equiv (c[i]-c[N-i-1])\cdot inv(2)b[i]≡(c[i]−c[N−i−1])⋅inv(2) 。和之前一样, m=2m=2m=2 时无逆特殊处理即可。
代码:
#include <bits/stdc++.h>
#define ll long long
#define endl '\n'
using namespace std;
const int N = 1e5 + 10;ll n, m;
ll a[N], b[N], c[N];ll qmi(ll a, ll b) //快速幂求逆元
{ll res = 1;a = (a % m + m) % m;while (b){if (b & 1) res = res * a % m;a = a * a % m;b >>= 1;}return res;
}bool check()
{for (int i = 1; i <= n; i++)if (c[i] != c[n - i + 1])return false;return true;
}int main()
{ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);cin >> n >> m;for (int i = 1; i <= n; i++){cin >> c[i];}if (m == 2){if (check()){cout << "Yes" << endl;for (int i = 1; i <= n; i++)cout << c[i] << ' ';cout << endl;for (int i = 1; i <= n; i++)cout << 0 << ' ';cout << endl;}else cout << "No" << endl;}else {ll inv2 = qmi(2, m - 2); //对2特判处理for (int i = 1; i <= n; i++){a[i] = (c[i] + c[n - i + 1]) * inv2 % m;b[i] = (c[i] + m - c[n - i + 1]) * inv2 % m;}cout << "Yes" << endl;for (int i = 1; i <= n; i++)cout << a[i] << ' ';cout << endl;for (int i = 1; i <= n; i++)cout << b[i] << ' ';cout << endl;}return 0;
}
C. 清楚姐姐学01背包(Easy Version)(01背包)
题意:
有 nnn 个物品,每个物品的体积为 www ,价值为 vvv ,背包的容量为 mmm 。
可以从 nnn 个物品中任选若干个放入背包,要保证总体积不能超过背包容量。
现定义背包中所放物品价值总和的最大值为 VVV ,从这 nnn 个物品中去掉某一个物品后,从剩余 n−1n - 1n−1 个物品中任选若干个放入背包,后来所放物品价值总和的最大值为 V′V'V′ 。
若 V′<VV' < VV′<V ,则称这个物品为必选物品。
求出对于每一个物品,它的价值再加上多少,能称为一个必选物品。
思路:
比普通的 01 背包题多了一个条件。
枚举每个物品,除了这个物品外,计算其他物品的01背包,再判断该物品是否必须取,它还需加上的价值就是 V - V' 。
代码:
#include <bits/stdc++.h>
#define ll long long
#define endl '\n'
using namespace std;
const int N = 110;int n, m;
ll w[N], v[N];int main()
{ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);cin >> n >> m;for (int i = 1; i <= n; i++){cin >> w[i] >> v[i];}for (int i = 1; i <= n; i++){vector<ll> dp(m + 1);for (int j = 1; j <= n; j++){if (i != j){for (int k = m; k >= w[j]; k--){dp[k] = max(dp[k], dp[k - w[j]] + v[j]);}}}ll res = dp[m] - (dp[m - w[i]] + v[i]) + 1;if (res < 0) cout << 0 << endl;else cout << res << endl;}return 0;
}
D. 清楚姐姐学01背包(Hard Version)(01背包)
题意:
与 C 题一样,不同的是数据范围变大。 (1≤n,m≤5000)(1 \le n, m \le 5000)(1≤n,m≤5000)
思路:
歪门邪道法:
类似于上题,既然琺暴力,那就分组求背包,以 75 个为一组,分成 75 个背包,第 iii 个背包中不含第 iii 组的物品。
其中对于第 jjj 个物品,找到其所在组数,把这组除了 jjj 以外的物品装入背包,再使用 C 题的方法判断即可。
再放上正经的解法:出题人题解
代码:
#include <bits/stdc++.h>
#define ll long long
#define endl '\n'
using namespace std;
const int N = 5010;int n, m;
ll w[N], v[N];int main()
{ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);cin >> n >> m;vector dp(76, vector<ll>(m + 1));for (int i = 1; i <= n; i++){cin >> w[i] >> v[i];int t = i / 75;for (int k = 0; k < 75; k++){if (k != t){for (int j = m; j >= w[i]; j--){dp[k][j] = max(dp[k][j], dp[k][j - w[i]] + v[i]);}}}}for (int i = 1; i <= n; i++){int t = i / 75;auto f = dp[t];for (int j = 1; j <= n; j++){if (i != j && t == j / 75){for (int k = m; k >= w[j]; k--){f[k] = max(f[k], f[k - w[j]] + v[j]);}}}ll ans = f[m] - f[m - w[i]] - v[i] + 1;if (ans < 0) cout << 0 << endl;else cout << ans << endl;}return 0;
}
E. 清楚姐姐打怪升级(数学 or 二分)
题意:
打怪游戏,有 nnn 只怪物,每只怪物的生命上限为 hhh ,生命每时刻恢复 vvv 点。
每次攻击的间隔为 ttt ,攻击力为 aaa 。
在每个时刻初,若怪物的生命值不满,则恢复 vvv 点生命值,但是不能超过生命值上限 hhh 。
每次攻击可以选择一只怪物造成 aaa 点伤害,若此时怪物生命值小于等于 000 ,则怪物死亡。
现在问至少在第几个时刻末可以杀死所有怪物,若永远无法杀死所有怪物则输出 −1-1−1 。
思路:
已知 nnn 只怪物的血量,回血速度,自身攻击力和攻击间隔,求打死所有怪物的时间。(注意,攻击是从时刻 111 开始的)
如果不能一刀解决,那么该怪物必定会经过 掉血 + 回血 的循环。
因此先把最后一刀减去,然后计算剩下的血量何时能扣完。
假设砍一刀后血量为 w=a−vw = a - vw=a−v ,如果 w≤0w \le 0w≤0 则无解,否则计算总轮数 s=⌈hw⌉+1s = \lceil \frac{h}{w}\rceil + 1s=⌈wh⌉+1 ,时间为 (s−1)⋅t+1(s - 1)·t + 1(s−1)⋅t+1 。
也可以二分计算:
二分恰好 xxx 次打死怪物,那么 check 时,前面已经攻击了 x−1x - 1x−1 次,加上血量回复,再补上第 xxx 次攻击,若怪物血量 h≤0h \le 0h≤0 ,则 check = true 。
代码:
#include <bits/stdc++.h>
#define ll long long
#define endl '\n'
using namespace std;
const int N = 1e5 + 10;ll n, t, a;
ll h[N], v[N];bool check()
{for (int i = 1; i <= n; i++){if (a <= v[i] && a < h[i])return false;}return true;
}int main()
{cin >> n >> t >> a;for (int i = 1; i <= n; i++){cin >> h[i] >> v[i];v[i] *= t;}if (!check()){cout << -1 << endl;}else{ll res = 0;for (int i = 1; i <= n; i++){if (h[i] <= a) res++;else {ll w = a - v[i];res += (h[i] - a + w - 1) / w + 1; //向上取整}}cout << (res - 1) * t + 1 << endl;}return 0;
}
F. 清楚姐姐学树状数组(二叉树 + DFS)
题意:
有一个尺寸大小为 N=2kN=2^{k}N=2k 的树状数组,按照如下的规则构造出一个"树状数组二叉树"。
-
编号为 iii 的节点的深度为 log2(lowbit(N))−log2(lowbit(i))log2(lowbit(N))-log2(lowbit(i))log2(lowbit(N))−log2(lowbit(i)) 。
-
整棵二叉树的中序遍历节点编号顺序为 1,2,3...N−1,N1,2,3...N-1,N1,2,3...N−1,N 。
问对于树状数组生成的二叉树上编号为 xxx 的节点,分别在前序、中序、后序遍历中是第几个被遍历到的节点?
思路:
给一个树状数组,建成一个二叉树,查询若干个节点的前中后序遍历。
树状数组中的两条重要路径为 x→x+lobit(x)x→x+lobit(x)x→x+lobit(x) 和 x→x−lobit(x)x→x-lobit(x)x→x−lobit(x)
- 当一个节点是左孩子时,其父节点是 x→x+lobit(x)x→x+lobit(x)x→x+lobit(x)
- 当一个节点是右孩子时,其父节点是 x→x−lobit(x)x→x-lobit(x)x→x−lobit(x)
因为长度大小为 2k2^k2k 的树状数组除根节点外都是全满的,大小实际上就是 2m−12^m − 12m−1 可以直接计算,所以 DFS 模拟前序和后序的过程中跳过整颗的子树部分直接计算答案即可。
代码:
#include <bits/stdc++.h>
#define ll long long
#define endl '\n'
using namespace std;
const int N = 2010;ll k, q;
ll n;ll lowbit(ll x)
{return x & -x;
}ll size(ll x)
{return (lowbit(x) << 1) - 1;
}bool is_lchild(ll x)
{return !(x & (lowbit(x) << 1));
}ll fa(ll x)
{if (is_lchild(x))return x + lowbit(x);return x - lowbit(x);
}ll lch(ll x)
{return x ^ lowbit(x) ^ (lowbit(x) >> 1);
}ll rch(ll x)
{return x ^ (lowbit(x) >> 1);
}ll L(ll x)
{ll root = n, ret = 1;while (root != x){ret++;if (x < root){root = lch(root);}else {ret += size(lch(root));root = rch(root);}}return ret;
}ll R(ll x)
{if (x == n) return n;ll root = x, ret = size(root);while (root != n){if (root == rch(fa(root))){ret += size(lch(fa(root)));}root = fa(root);}return ret;
}int main()
{ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);cin >> k >> q;n = 1ll << k;while (q--){ll x;cin >> x;cout << L(x) << ' ' << x << ' ' << R(x) << endl;}return 0;
}
G. 清楚姐姐逛街(Easy Version)(BFS)
题意:
A,B 两人走地图,要求 B 在最短的时间内追上 A 。
地图可以视为是一个 N⋅MN \cdot MN⋅M 的二维平面,左上角为坐标原点 (0,0)(0,0)(0,0) ,向下为 xxx 轴正方向,向右为 yyy 轴正方向,入口位于点 s(xs,ys)s(x_s,y_s)s(xs,ys) 。
地图行走规则如下:
‘L’ – 向左,‘R’ – 向右,‘U’ – 向上,‘D’ – 向下
‘.’ – 表示终止位置,当移动到这里后将永远停在该位置
‘#’ – 表示墙壁,任何人都不能移动到这里
B 追 A,且 B 可以随意移动或停在原地,不必遵守地图的规则。
B 从入口处出发,有 QQQ 次询问,每次输入一个坐标表示 A 从该位置开始移动,问至少要多久才能追上 A ,若无论如何都追不上则输出 -1.
思路:
首先预处理 B 到达每个位置所花费的时间,因为 B 可以随便走,所以先用 BFS 遍历连通块,计算到达每个位置的时间。
然后对于每次询问,A 按照地图规则来走,直到 A到达某个位置的时间 ≥ B到达的时间,则 B 能追上 A 。
代码:
#include <bits/stdc++.h>
#define ll long long
#define endl '\n'
#define PII pair<int, int>
using namespace std;
const int N = 810;int n, m, sx, sy, Q;
char mp[N][N];
int d[N][N];void bfs()
{queue<PII> q;q.push({sx, sy});d[sx][sy] = 0;while (!q.empty()){int x = q.front().first, y = q.front().second;q.pop();int dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1};for (int i = 0; i < 4; i++){int xx = x + dx[i], yy = y + dy[i];if (xx >= 1 && xx <= n && yy >= 1 && yy <= m && d[x][y] + 1 < d[xx][yy] && mp[xx][yy] != '#'){d[xx][yy] = d[x][y] + 1;q.push({xx, yy});}}}
}int main()
{memset(d, 63, sizeof d);cin >> n >> m >> sx >> sy >> Q;sx++, sy++;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)cin >> mp[i][j];bfs();while (Q--){int x, y;cin >> x >> y;x++, y++;int f = 1, res = 1;while (1){int lax = x, lay = y;if (mp[x][y] == 'U' && mp[x - 1][y] != '#') x--;else if (mp[x][y] == 'D' && mp[x + 1][y] != '#') x++;else if (mp[x][y] == 'R' && mp[x][y + 1] != '#') y++;else if (mp[x][y] == 'L' && mp[x][y - 1] != '#') y--;if (lax == x && lay == y){if (d[x][y] >= 1e9){f = 0;break;}}if (d[x][y] <= res){res = max(d[x][y], res);break;}res++;}if (!f) cout << -1 << endl;else cout << res << endl;}return 0;
}
L. 清楚姐姐的三角形I(数学 + 推公式)
题意:
假设三角形的三条边的长度分别为 a,b,ca,b,ca,b,c 。
定义三角形的三个顶点分别为 A,B,CA,B,CA,B,C,顶点 AAA 连接 b,cb,cb,c 两边;顶点 BBB 连接 a,ca,ca,c 两边;顶点 CCC 连接 a,ba,ba,b 两边。
定义三角形三个顶点的权值 VA=lb+lc,VB=la+lc,VC=la+lbV_A=l_b+l_c,V_B=l_a+l_c,V_C=l_a+l_bVA=lb+lc,VB=la+lc,VC=la+lb 。
现在给定 VA,VB,VCV_A,V_B,V_CVA,VB,VC 的值,求 a,b,ca,b,ca,b,c 的值。
思路:
我们根据三角形已知条件推出三条边的表达式:
a=(vb+vc−va)/2a = (v_b + v_c - v_a) / 2a=(vb+vc−va)/2
b=(va+vc−vb)/2b= (v_a + v_c - v_b) / 2b=(va+vc−vb)/2
c=(va+vb−vc)/2c = (v_a + v_b - v_c) / 2c=(va+vb−vc)/2
然后根据组成三角形的条件:任意两边之和大于第三边,任意两边之差小于第三边
判断这三条边能否组成三角形即可。
代码:
#include <bits/stdc++.h>
#define ll long long
#define endl '\n'
using namespace std;
const int N = 2e5 + 10;void solve()
{ll va, vb, vc;cin >> va >> vb >> vc;ll s = (va + vb + vc) / 2;if (s < 3){cout << "NO" << endl;}else {ll a = (vb + vc - va) / 2;ll b = (va + vc - vb) / 2;ll c = (va + vb - vc) / 2;if (a + b > c && b + c > a && c + a > b&& abs(a - b) < c && abs(b - c) < a && abs(c - a) < b&& va == b + c && vb == a + c && vc == a + b){cout << "YES" << endl;cout << a << ' ' << b << ' ' << c << endl;}else {cout << "NO" << endl;}}
}int main()
{ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);int t;cin >> t;while (t--){solve();}return 0;
}
M. 清楚姐姐的三角形II(构造)
题意:
要求构造一个大小为 nnn 的数组,满足数组中每相邻的三项均不能组成三角形,输出这个数组。
思路:
你以为是斐波那契???NoNoNo,请下载国家反诈APP.
题目只要求相邻三项无法构成三角形,条件很少,怎么样构造都可以。
我们任意选三个不能组成三角形的数循环就行了,这里用的是 1 1 2 。
代码:
#include <bits/stdc++.h>
#define ll long long
#define endl '\n'
using namespace std;
const int N = 1e5 + 10;int a[N];int main()
{int n;cin >> n;for (int i = 1; i <= n; i++){if (i % 3) cout << 1 << ' ';else cout << 2 << ' ';}cout << endl;return 0;
}
相关文章:

2023牛客寒假算法集训营4
目录A. [清楚姐姐学信息论](https://ac.nowcoder.com/acm/contest/46812/A)(数学)B. [清楚姐姐学构造](https://ac.nowcoder.com/acm/contest/46812/B)(数学 构造)C. [清楚姐姐学01背包(Easy Version)](https://ac.nowcoder.com/…...
vue组合式API及生命周期钩子函数
一、组合式API 什么是组合式API? vue3中支持vue2的选项式、支持新的编程模式–函数式编程(没有this指针)做了一个兼容,可以在一个组件中使用函数式编程和OOP编程(选项式) setup()函数 可以使用setup属性…...

Python|每日一练|数组|回溯|二分查找|排序和顺序统计量|.update方法 |单选记录:组合总和|寻找峰值|编程通过键盘输入每一位运动员
1、组合总和(数组、回溯) 给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的数字可以无限制重复被选取。 说明: 所有数字(包括 t…...
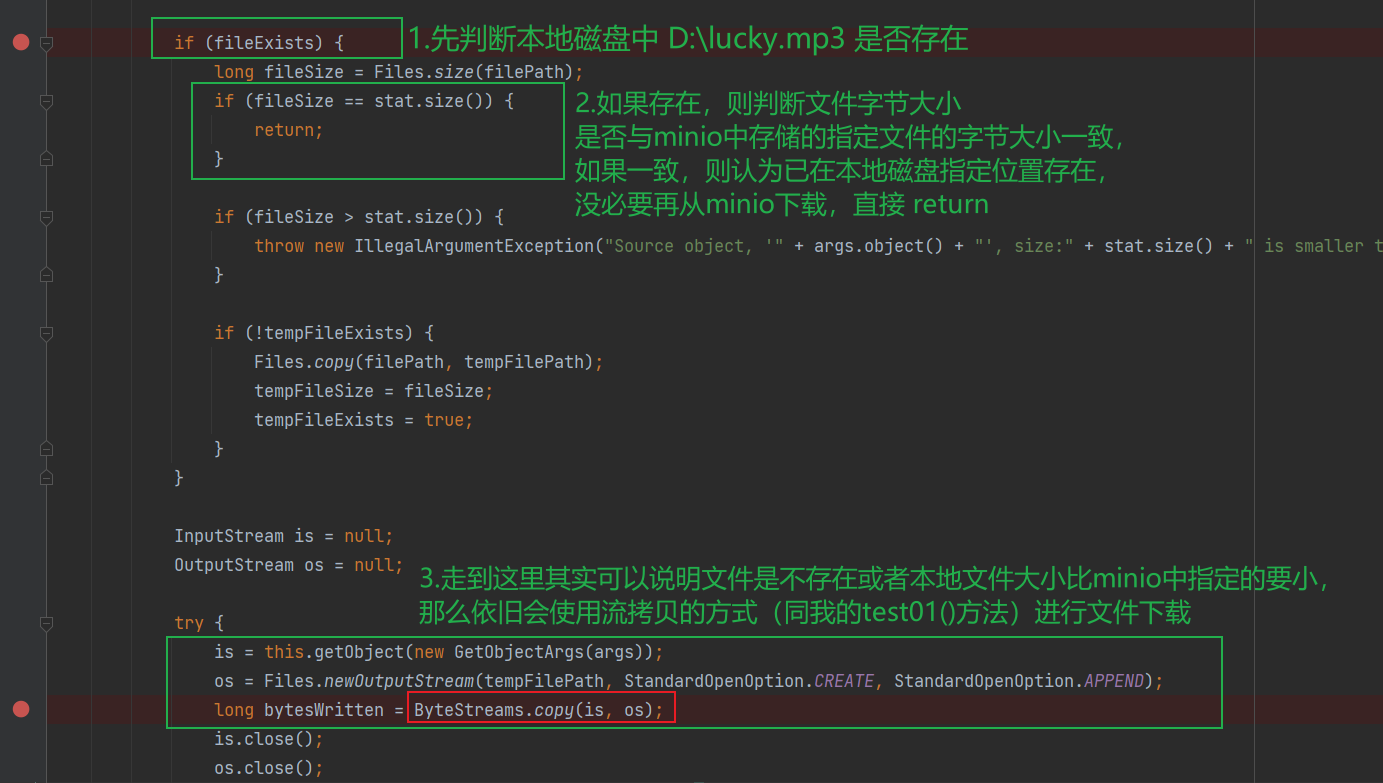
minio下载文件速度很慢的原因分析与说明
文章目录1.实战背景2.问题描述3.问题分析4.问题解决1.实战背景 最近在做一个项目,需要用到minio来搭建文件系统,先简单说一下我在项目中设置的上传文件流程: 前端将分块文件逐一传给后端,后端再存储到 linux服务器的minio 当中。…...

基于comsol软件弯曲单模光纤模拟仿真
在本节中,主要基于实验室实际光纤单模圆柱光纤进行模拟,与comsol案例库文件在分析过程和建模有些差异: 模拟主要通过以下三个步骤进行:模型的几何构建、物理场的添加研究、结构处理分析来进行。 下面是第一步骤:几何…...

如何开启多个独立Chrome浏览器
一、简介 作为测试或者开发人员,有些情况下会用到 Chrome 浏览器,但有时是同一个 Chrome 浏览器无法为我们提供隔离开的不同环境。这样 我们就需要清理 cache 、切换账号等,降低了我们的工作效率。今天的主题是如何开启多个独立的 Chrome 浏…...

erp5开源制造业erp主要业务会计分录处理
erp5开源制造业erp主要业务会计分录处理 采购业务的会计分录 收到发票时 借:材料采购 (1201) 应交税费-应交增值税(进项税)(21710101) 贷:应付账款 (2121) 付款时 借:应付账款 (2121) 贷:银行存款 (1002) 入…...
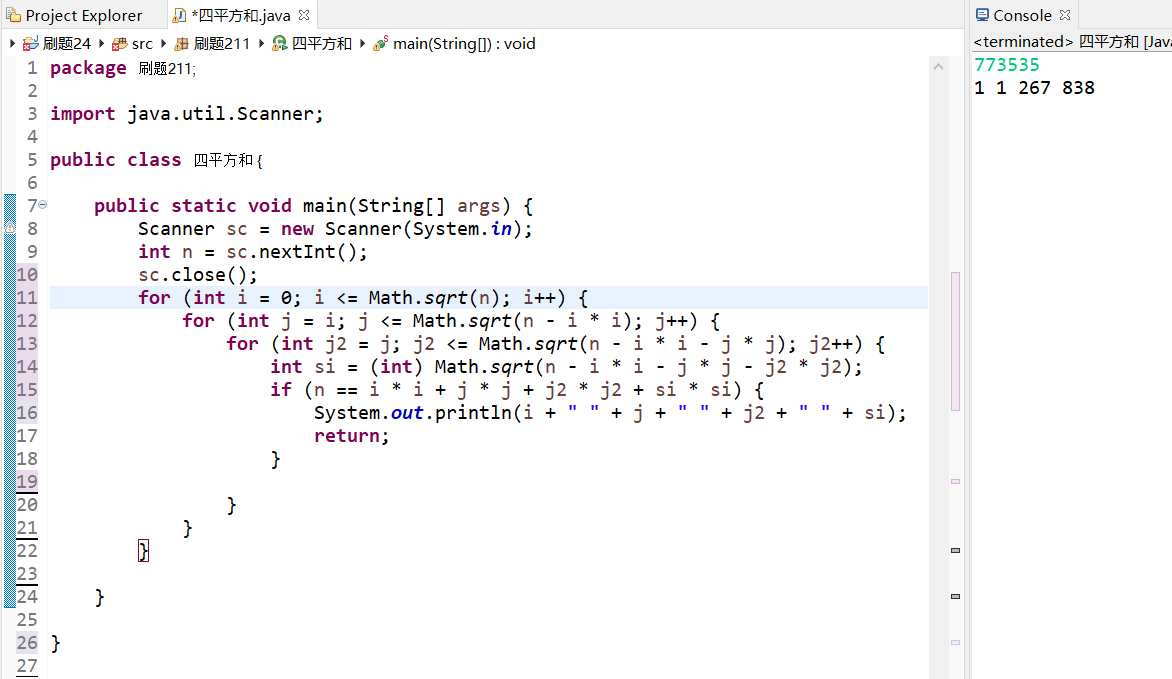
技能树基础——17四平方和(拉格朗日定理,嵌套循环)
题目:四平方和定理,又称为拉格朗日定理:每个正整数都可以表示为至多4个正整数的平方和。如果把0包括进去,就正好可以表示为4个数的平方和。比如:5 0^ 2 0^ 2 1^ 2 2^27 1^ 2 1^ 2 1^ 2 2^2 (^符号表…...

JPA、EJB、事物管理---相关内容整理
目录 ■前言 ■实现原理:容器管理事务 ■代码实现简单描述: 1.JPA ■定义 ■1.1.配置文件 ■1.2.OSS jar ■1.3.一些OPA的类(举例) ■1.4. jpa 框架在实体类(Entity)中添加非数据库字段的属性--…...
C语言学习笔记(一):了解C语言
什么是C语言 C语言是一种高级编程语言,最早由丹尼斯里奇在1972年开发。它是一种通用编程语言,提供了高级编程语言的方便和易用性,同时又有较低级别的编程语言的灵活性和效率。C语言在许多操作系统、编译器和应用程序开发中广泛使用ÿ…...

回头看——《智能家居项目小结》
openAI兴起,于是拿着之前小组合作的项目(承认优化较差),交给AI试着帮忙优化下1.功能函数(TCP_SER_INIT)优化源代码:int TCP_SER_INIT(int *tcpsocket, const char *ip, const char *…...
社交登陆OAuth2.0
QQ、微博、github 等网站的用户量非常大,别的网站为了 简化自我网站的登陆与注册逻辑,引入社交登陆功能; 步骤: 1)、用户点击 QQ 按钮 2)、引导跳转到 QQ 授权页 3)、用户主动点击授权ÿ…...
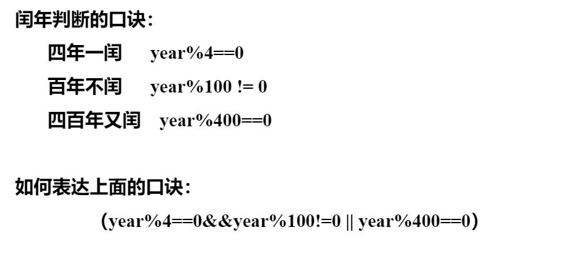
C++005-C++选择与分支2
文章目录C005-C选择与分支2条件语句C实现else if 语句题目描述 根据成绩输出成绩等级ABCDEif嵌套语句题目描述 输出三个数中的最大值题目描述 模拟游戏登录switch语句三元运算符题目描述 输出三个数中的最大值-基于3元运算符题目描述 根据1-7输出星期1-星期日案例练习题目描述 …...

IPFS 简介及概述
文章目录 IPFS 简介IPFS 包含的协议内容及其理解IPFS 和 BitTorrent 区别IPFS 简介 星际文件系统(InterPlanetary File System). IPFS 是一个分布式的网络文件系统, 点到点超媒体协议. 可以让我们的互联网速度更快, 更加安全, 并且更加开放. IPFS协议的目标是取代传统的互联网…...

初学者必读:讲解 VC 下如何正确的创建、管理及发布项目
Visual C 的项目文件组成,以及如何正确的创建及管理项目。 本内容是初学者必须要掌握的。不能正确的管理项目,就不能进一步写有规模的程序。 一、项目下各种常见文件类型的功能 1. 代码文件 扩展名为 .cpp、.c、.h 等。 通常情况下,项目…...

剑指offer(中等)
目录 二维数组中的查找 重建二叉树 矩阵中的路径 剪绳子 剪绳子② 数值的整数次方 表示数值的字符串 树的子结构 栈的压入、弹出序列 从上到下打印二叉树① 从上到下打印二叉树③ 二叉搜索树的后序遍历序列 二叉树中和为某一值的路径 复杂链表的复制 二叉搜索树与…...
微软发布会精华回顾:“台式电脑”抢了风头
Lightbot北京时间2016年10月26日晚10点,微软在纽约发布了名为 Surface Studio 的一体机、名为 Surface Dial 的配件以及外观未变的顶配版 Surface Book。同时,微软宣布了 Windows 10 下一个重要版本——“Creators Update”的数项新功能,包括…...

CF1561C Deep Down Below 题解
CF1561C Deep Down Below 题解题目链接字面描述Deep Down Below题面翻译题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示思路TLE算法具体思想TLE特例AC思想代码实现备注题目 链接 https://www.luogu.com.cn/problem/CF1561C 字面描述 Deep Down Below 题面翻译…...

秒杀项目之服务调用分布式session
目录 nginx动静分离 服务调用 创建配置zmall-cart购物车模块 创建配置zmall-order订单模块 服务调用 spring session实战 什么是Spring Session 为什么要使用Spring Session 错误案例展示 配置spring-session 二级域名问题 用户登录 nginx动静分离 第1步ÿ…...
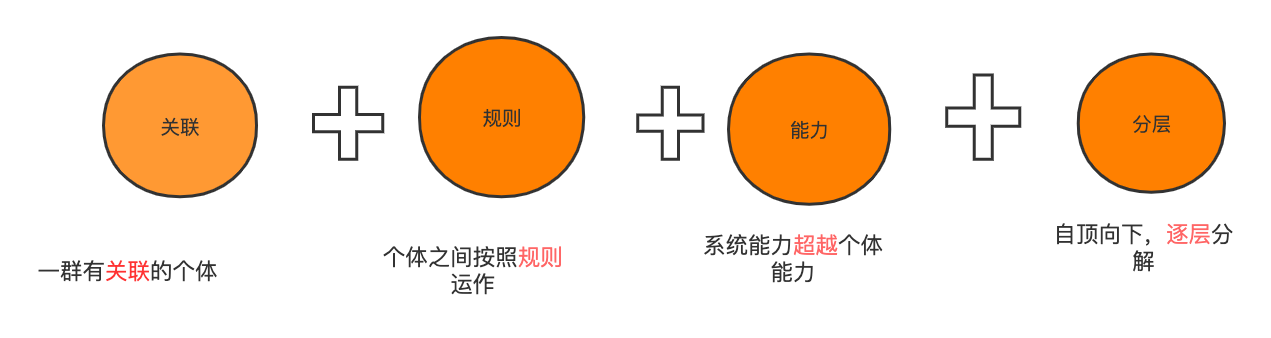
聊聊什么是架构,你理解对了吗?
什么是架构?软件有架构?建筑也有架构?它们有什么相同点和不同点? 下面咱们就介绍一下,容易混淆的几个概念 一、系统与子系统 系统 泛指由一群有关联的个体组成,根据某种规则运作,能完成个别元件不能单独完成的工作的群体。它的意思是 “总体”、“整体”或“联盟” 子系…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
