python 基础知识点(蓝桥杯python科目个人复习计划59)
今日复习内容:做题
例题1:建造房屋
问题描述:
小蓝和小桥是两位年轻的建筑师,他们正在设计一座新的城市。
在这个城市中,有N条街道,每条街道上有M个位置可以建造房屋(一个位置只能建造一个房屋),建造一个房屋的费用是1元,小蓝和小桥共有k元的建造预算。
现在,他们想知道,一共有多少种建造方案,满足以下要求:
在每条街道上,至少建造一座房屋;
建造的总成本不能超过k元。
由于方案数可能很大,他们只需要输出答案对10^9 + 7取模的结果。
输入格式:
一行3个整数N,M(1 = N,M <= 30)和K(1 <= K <= N * M),分别表示街道数,街道位置数和预算。
输出格式:
一个整数,表示满足条件的方案数对10^9 + 7取模的结果。
参考答案:
mod = int(1e9) + 7
n,m,k = map(int,input().split())
f = [[0] * (k + 1) for i in range(n + 1)]
for i in range(k + 1):f[0][i] = 1
for i in range(1,n + 1):for j in range(k + 1):for z in range(1,m + 1):if j >= z:f[i][j] = (f[i][j] + f[i - 1][j - z]) % mod
print(f[n][k])运行结果:

以下是我对此题的理解:
这道题涉及动态规划,目标的计算在给定预算下,满足建造要求的方案数。
1.定义了一个二维数组f,其中f[i][j]表示在前i条街道上,总成本为j的方案数。
2.初始化数组f[0][i],表示在0条街道上,总成本为i的方案数,初始化为1,因为无论预算多少,都有一种方案(不建造任何房屋)。
3.使用3层循环,其中第一层循环遍历街道,第二层循环遍历总成本,第3层循环遍历每个街道上可建造的位置。
4.在内层循环中,检查当前总成本j是否大于街道上可建造的位置数z。如果满足条件,则需要更新f[i][j],加上之前街道i - 1上总成本为j - z的方案数。
5.最终输出结果为f[n][k],表示在前n条街道上,总成本为k的方案数。
n,m,k = map(int,input().split()):从标准输入读取三个整数,分别表示街道数n,街道位置数m和预算k
f = [[0] * (k + 1) for i in range(n + 1):这一行代码创建了一个二维列表f,其中包含n + 1行,每行包含k + 1个元素,初始值都为0,这个列表用于存储动态规划过程中的中间结果。
for i in range(k + 1):这个循环遍历了k + 1个预算值,用于初始化第0条街道上的方案数。
f[0][i] = 1:这一行将第0条街道上总成本为i的方案数记为1,因为无论预算多少,都要一个方案,不建造任何房屋。
for i in range(1,n + 1):这个循环遍历了1到n条街道
for j in range(k + 1):这个循环遍历了k + 1个总成本值,,用于计算每条街道上的方案数
for z in range(1,m + 1):这个循环遍历了每个街道上可建造的位置数,从1到m
if j >= z:这个条件判断语句检查当前总成本j是否大于等于当前街道上可建造的位置数z
f[i][j] = (f[i][j] + f[i - 1][j - z]) % mod:这一行更新了当前街道上总成本为j的方案数。它将之前街道i - 1上总成本为j - z的方案数加到当前街道上,并对结果取模。
print(f[n][k]):最后输出结果,表示前n条街道上,总成本为k的方案数。
例题2:破损的楼梯
问题描述:
小蓝来到了一座高耸的楼梯前,楼梯共有N级台阶,从第0级台阶出发。小蓝可以迈上1或2级台阶。但是,楼梯上的第a1级,第a2级,第a3级,以此类推,共M级台阶的台阶面坏掉了,不能踩上去。
现在,小蓝想要到达楼梯的顶端,也就是第N级台阶,但他不能踩到坏了的台阶上,请问他有多少种不能踩到坏了的楼梯但是能到达第N级台阶的方案数?
由于方案数很大,请输出其对10^9 + 7的结果。
输入格式:
第一行包含两个正整数N(1 <= N <= 10^5)和M(0 <= M <= N),表示台阶总数和坏了的台阶级数。
接下来来N行,包含N个整数a1,a2,...,aM,(1 <= a1 < a2 <... < aM <= N),表示坏掉的台阶编号。
输出格式:
输出一个整数,表示小蓝到达楼梯顶层的方案数,对10^9 + 7取模。
参考答案:
mod = int(1e9) + 7
n,m = map(int,input().split())
mm = list(map(int,input().split()))
vis = [0] * (n + 1)
for i in mm:vis[i] = 1
f = [0] * (n + 1)
f[0] = 1
f[1] = 1 - vis[1]
for i in range(2,n + 1):if not vis[i]:f[i] = (f[i - 1] + f[i - 2]) % mod
print(f[n])运行结果:
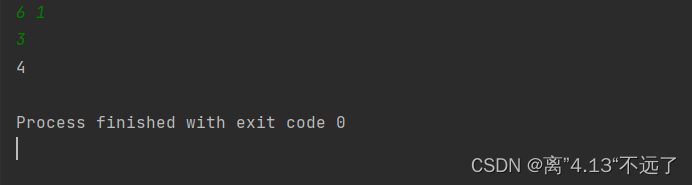
以下是我对此题的理解:
这个题是一个很经典的冬天规划问题,以下是我的思路:
n,m = map(int,input().split()):从标准输入中读取两个整数,分别表示台阶总数和坏了的台阶数。
mm = list(map(int,input().split())):从输入中读取坏了的台阶的编号,并将它们储存在列表mm中
vis = [0] * (n + 1):创建了一个长度为n + 1的列表,用于标记每个台阶是否坏掉。如果台阶i坏了,则vis[i]的值为1,否则为0.
for i in mm:vis[i] = 1:这个循环将坏掉的台阶编号所对应的vis列表中的值记为1,表示这些台阶坏了。
f = [0] * (n + 1):用于存储动态规划过程中的中间结果,f[i]表示到达第i级台阶的方案数
f[0] = 1:初始第0级 台阶的方案数为0,因为小蓝从第0级台阶出发。
f[1] = 1 - vis[1]:初始化第一级台阶的方案数,如果第一级台阶坏了,则方案数为0,否则为1.
for i in range(2,n + 1):遍历剩下的台阶
if not vis[i]:用于判断此台阶是否坏了,如果没有,就继续执行下面的代码
f[i] = (f[i - 1] + f[i - 2]) % mod:这一行更新了到达第i级台阶的方案数,如果第i - 1级台阶坏了,只能通过第i - 2级台阶才能到达第i级台阶,这里需要考虑台阶的可行性。
print(f[n]):最终输出结果
例题3:拍照
问题描述:
小椒是个摄影爱好者。恰逢班级合照,他受邀帮忙拍照(站成一排)。这本是一件简单的事,但由于啾啾是个完美主义者,他希望拍的照片必须符合美学,即存在一个身高较大值,使得较大值无论往左还是往右身高都是递减的,数学上可以表示为:a[1] <= ... <= a[i] >= a[i + 1] >= ...>= a[n]。同学们已经站好了,但是不符合美学,你需要找出尽可能少的同学出列重新进行排列。请问最少需要出列几个同学?
输入格式:
第一行输入n,表示有n个同学,接下来的n行,输入校友身高,其中第i行输入a[i]( 1 <= i <= n),输入编号为i的校友的身高(单位是毫米)。
(1 <= n <= 100,1500 <= a[i] <= 1900)
输出格式:
输出一个整数,表示最少需要出队多少个同学。
参考答案:
n = int(input())
a = list(map(int, input().split()))
dp1 = [0] * (n + 1)
dp2 = [0] * (n + 1)for i in range(1, n + 1):dp1[i] = 1for j in range(1, i):if a[i - 1] >= a[j - 1]:dp1[i] = max(dp1[i], dp1[j] + 1)for i in range(n, 0, -1):dp2[i] = 1for j in range(n, i, -1):if a[i - 1] >= a[j - 1]:dp2[i] = max(dp2[i], dp2[j] + 1)ans = 0
for i in range(1, n + 1):ans = max(ans, dp1[i] + dp2[i] - 1)print(n - ans)运行结果:
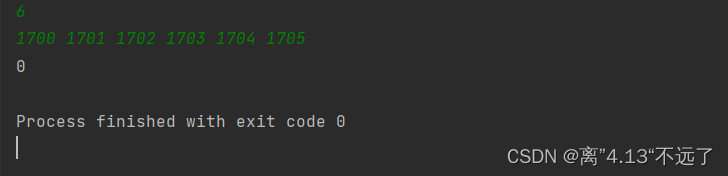
以下是我对此题的理解:
n = int(input()):从标准输入读取同学的数量n
a = list(map(int,input().split())):从标准输入读取每个同学的身高,并将它们存储在列表a中
dp1和dp2分别代表从左到右和从右到左的动态规划数组。它们的长度都是n + 1,用于存储每个位置的最长符合美学要求的子序列长度。
对于dp1数组,dp1[i]表示以同学i为结束的最长符合美学要求的子序列长度,初始化所有值为1,因为每个同学本身就是一个符合美学要求的子序列
对于dp2数组,dp2[i]表示以同学i为开始的最长符合美学要求的子序列长度,初始化所有值为1,因为每个同学本身就是一个符合美学要求的子序列。
对于每个同学i,在dp1中遍历所有在i之前的同学j,之后就是比较,再输出答案就可以了。
OK,前几天写比赛论文去了,没时间复习,从今天开始,必须挤时间了。
那这篇就这样了,下一篇继续!
相关文章:

python 基础知识点(蓝桥杯python科目个人复习计划59)
今日复习内容:做题 例题1:建造房屋 问题描述: 小蓝和小桥是两位年轻的建筑师,他们正在设计一座新的城市。 在这个城市中,有N条街道,每条街道上有M个位置可以建造房屋(一个位置只能建造一个房…...
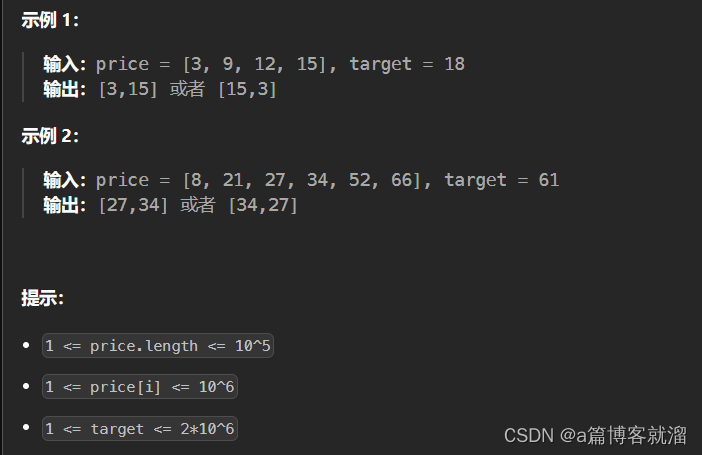
LCR 179. 查找总价格为目标值的两个商品 - 力扣
1. 题目 购物车内的商品价格按照升序记录于数组 price。请在购物车中找到两个商品的价格总和刚好是 target。若存在多种情况,返回任一结果即可。 2. 示例 3. 分析 题目有说明为递增数组,所以可以利用单调性双指针解决。跟611. 有效的三角形个数为一类题…...
《汇编语言》- 读书笔记 - 第16章-直接定址表
《汇编语言》- 读书笔记 - 第16章-直接定址表 16.1 描述了单元长度的标号(数据标号)检测点 16.1 16.2 在其他段中使用数据标号assume通过标号取地址检测点 16.2 16.3 直接定址表(Direct Addressing Table)例1分析代码效果 例2分析…...

ChatGPT 新增朗读功能,支持 37 种语言
3 月 5 日消息,OpenAI 为其广受欢迎的聊天机器人 ChatGPT 推出了名为「朗读」(Read Aloud) 的新功能。该功能可以让 ChatGPT 用五种不同的声音朗读其回复,旨在为用户提供更加便捷的交互体验。目前,「朗读」功能已上线 ChatGPT 的网页端、iOS …...
洛谷 P8816 [CSP-J 2022] 上升点列(T4)
目录 题目传送门 算法解析 最终代码 提交结果 尾声 题目传送门 [CSP-J 2022] 上升点列 - 洛谷https://www.luogu.com.cn/problem/P8816 算法解析 k 0 且 xi, yi 值域不大时,这题是非常简单的 DP,类似「数字三角形」。 记 dp(x,y) 为「以 (x,y) …...
python爬虫(2)
继上节 查看数组维数 可以使用数组的ndim属性 代码示例如下: import numpy as np c np.random.randint(1,9,5) print(c.ndim) 结果如下: 当然这些也可以结合前面的各种用法来使用 1、选取数组元素 (1)一维数组的元素…...
外包干了8天,技术退步明显。。。。。
先说一下自己的情况,本科生,19年通过校招进入杭州某软件公司,干了接近3年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...
浅谈去耦电容的作用、选择、布局及其它电容的区别!
在一些文章资料中,去耦电容器被认为是旁路电容器。在其他资料中,去耦电容和旁路电容的区别在于:“旁路电容以输入信号中的干扰为滤波对象,而去耦电容以输出信号的干扰为滤波对象,防止干扰信号返回到输出端。”力量。”…...
抖音视频评论批量采集软件|视频下载工具
《轻松搞定!视频评论批量采集软件,助您高效工作》 在短视频这个充满活力和创意的平台上,了解用户评论是了解市场和观众心声的重要途径之一。为了帮助您快速获取大量视频评论数据,我们推出了一款操作便捷、功能强大的软件ÿ…...

javaSE-----继承和多态
目录 一.初识继承: 1.1什么是继承,为什么需要继承: 1.2继承的概念与语法: 二.成员的访问: 2.1super关键字 2.2this和super的区别: 三.再谈初始化: 小结: 四.初识多态: 4.1多…...

数据库之Oracle数据导入导出
目录 一、单表导出和导入1、单表导出数据2、单表导入数据二、全表导出和导入1、远程导出全表数据2、导入本地数据三、密码带特殊字符的写法1、Windows OS写法2、Linux/Unix OS写法 四、总结 一、单表导出和导入 1、单表导出数据 --导出远程服务上的表数据 exp 用户名/密码IP…...

nRF52832——GPIOTE与外部中断
这里写目录标题 GPIOTE 原理分析GPIOTE 输入事件应用GPIOTE 事件寄存器应用GPIOTE 事件组件的应用(库函数)GPIOTE PORT 事件应用 GPIOTE 任务应用GPIOTE 任务触发 LED 寄存器操作组件方式进行任务配置 GPIOTE 原理分析 GPIO 任务和时间(GPIO…...
根据用户名称实现单点登录
一、参数格式 二、后端实现 Controller层 public class IAccessTokenLoginController extends BaseController {Autowiredprivate ISysUserService sysUserService;Autowiredprivate ISingleTokenServiceImpl tokenService;/*** 登录方法** return 结果*/PostMapping("/l…...

【设计】855. 考场就座
855. 考场就座 这段代码实现了一个考场安排座位的算法。在这个算法中,考场被模拟成一个从0到n-1的数轴,其中每个位置代表一个座位。目的是在每次学生入座时,找到一个使得所有学生之间距离最大化的座位,并在学生离开时更新座位信息…...
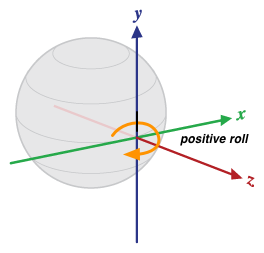
Android中的传感器类型和接口名称
本文将介绍传感器坐标轴、基础传感器和复合传感器(动作传感器、姿势传感器、未校准传感器和互动传感器)。 1. 传感器坐标轴 许多传感器的传感器事件值在相对于设备静止的特定坐标系中表示。 1.1 移动设备坐标轴 Sensor API 仅与屏幕的自然方向相关&a…...

解析进程 /proc/pid/maps 和 /proc/pid/smaps
目录 /proc//maps 背景 具体描述 代码实现 实践 /proc/pid/smaps smaps各子项详解 代码实现 代码调用的路径如下: 小结 /proc/<pid>/maps 背景 相对于/proc/meminfo和dumpsys meminfo可以看到系统整体的内存信息,我们还需要能够具体到…...
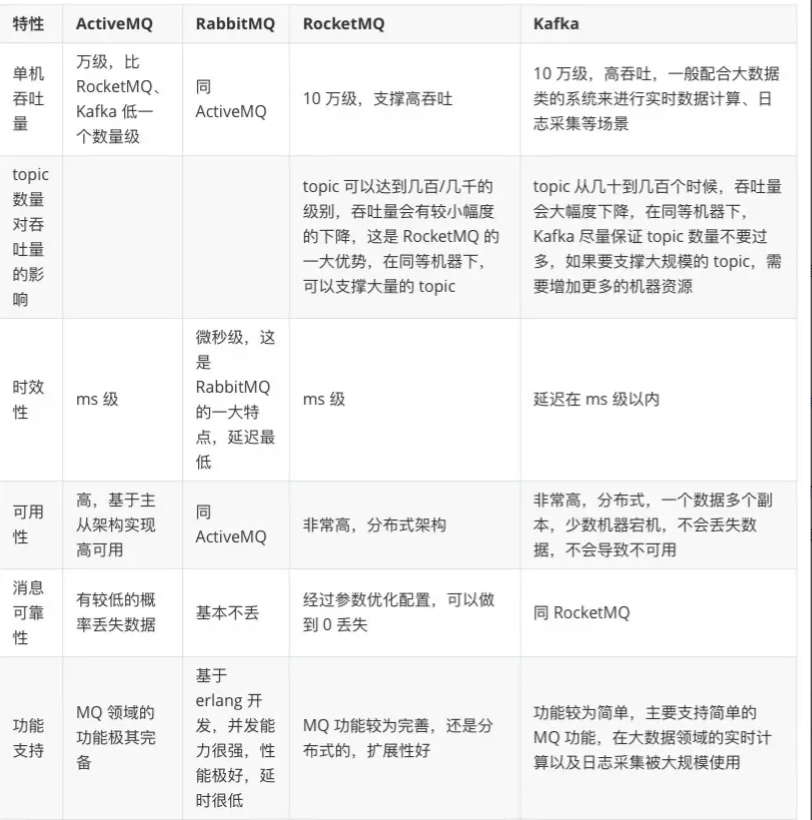
【MQ】消息队列概述
📝个人主页:五敷有你 🔥系列专栏:MQ ⛺️稳中求进,晒太阳 定义 消息队列:一般我们简称为MQ(Message Queue) Message Queue :消息队列中间件,很多初学者认为,MQ通过消息的发送…...
交友盲盒系统PHP开源的盲盒源码
源码介绍: 交友盲盒系统是一款基于PHP开发的开源免费盲盒系统,旨在为用户提供一个充满乐趣和惊喜的社交体验。该系统具有丰富的功能和灵活的扩展性,可以轻松地满足各种线上交友、抽奖活动等场景的需求。 安装说明: PHP版本&…...

【Flutter 面试题】什么是异步编程 Flutter中如何处理异步操作?
【Flutter 面试题】什么是异步编程 Flutter中如何处理异步操作? 文章目录 写在前面解答补充说明从网络API异步获取数据并解析 写在前面 关于我 ,小雨青年 👉 CSDN博客专家,GitChat专栏作者,阿里云社区专家博主&#x…...

处理error: remote origin already exists.及其Gitee文件上传保姆级教程
解决error: remote origin already exists.: 删除远程 Git 仓库 git remote rm origin 再添加远程 Git 仓库 git remote add origin (HTTPS) 比如这样: 然后再push过去就ok了 好多人可能还是不熟悉怎么将文件上传 Gitee:我…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...
