代码随想录算法训练营第五十五天|583. 两个字符串的删除操作、72. 编辑距离。
583. 两个字符串的删除操作
题目链接:两个字符串的删除操作
题目描述:
给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。
每步 可以删除任意一个字符串中的一个字符。
解题思路:
1、确定dp数组(dp table)以及下标的含义
dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。
这里dp数组的定义有点点绕,大家要撸清思路。
2、确定递推公式
当word1[i - 1] 与 word2[j - 1]相同的时候
当word1[i - 1] 与 word2[j - 1]不相同的时候
当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
情况一:删word1[i - 1],最少操作次数为dp[i - 1][j] + 1
情况二:删word2[j - 1],最少操作次数为dp[i][j - 1] + 1
情况三:同时删word1[i - 1]和word2[j - 1],操作的最少次数为dp[i - 1][j - 1] + 2
那最后当然是取最小值,所以当word1[i - 1] 与 word2[j - 1]不相同的时候,递推公式:dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
因为 dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2,所以递推公式可简化为:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
这里可能不少录友有点迷糊,从字面上理解 就是 当 同时删word1[i - 1]和word2[j - 1],dp[i][j-1] 本来就不考虑 word2[j - 1]了,那么我在删 word1[i - 1],是不是就达到两个元素都删除的效果,即 dp[i][j-1] + 1。
3、dp数组如何初始化
从递推公式中,可以看出来,dp[i][0] 和 dp[0][j]是一定要初始化的。
dp[i][0]:word2为空字符串,以i-1为结尾的字符串word1要删除多少个元素,才能和word2相同呢,很明显dp[i][0] = i。
dp[0][j]的话同理
代码实现:
class Solution {public int minDistance(String word1, String word2) {int len1 = word1.length();int len2 = word2.length();int[][] dp = new int[len1 + 1][len2 + 1];for (int i = 1; i <= len1; i++) {for (int j = 1; j <= len2; j++) {if (word1.charAt(i - 1) == word2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);}}}return len1 + len2 - dp[len1][len2] * 2;}
}
72. 编辑距离
题目链接:编辑距离
题目描述:
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
解题思路:
递推公式:
1、if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑,dp[i][j] 就应该是 dp[i - 1][j - 1],即dp[i][j] = dp[i - 1][j - 1];
2、if (word1[i - 1] != word2[j - 1]),此时就需要编辑了。
操作一:word1删除一个元素,那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i - 1][j] + 1;
操作二:word2删除一个元素,那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i][j - 1] + 1;
操作三:替换元素,word1替换word1[i - 1],使其与word2[j - 1]相同,此时不用增删加元素。
可以回顾一下,if (word1[i - 1] = = word2[j - 1])的时候我们的操作 是 dp[i][j] = dp[i - 1][j - 1] 对吧。
那么只需要一次替换的操作,就可以让 word1[i - 1] 和 word2[j - 1] 相同。
所以 dp[i][j] = dp[i - 1][j - 1] + 1;
综上,当 if (word1[i - 1] != word2[j - 1]) 时取最小的,即:dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
代码实现:
class Solution {public int minDistance(String word1, String word2) {int m = word1.length();int n = word2.length();int[][] dp = new int[m + 1][n + 1];// 初始化for (int i = 1; i <= m; i++) {dp[i][0] = i;}for (int j = 1; j <= n; j++) {dp[0][j] = j;}for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {// 因为dp数组有效位从1开始// 所以当前遍历到的字符串的位置为i-1 | j-1if (word1.charAt(i - 1) == word2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1;}}}return dp[m][n];}
}
相关文章:

代码随想录算法训练营第五十五天|583. 两个字符串的删除操作、72. 编辑距离。
583. 两个字符串的删除操作 题目链接:两个字符串的删除操作 题目描述: 给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。 每步 可以删除任意一个字符串中的一个字符。 解题思路: 1、确定dp数组&#x…...
Softmax 回归 + 损失函数 + 图片分类数据集【动手学深度学习v2】李沐动手学深度学习课程笔记
目录 Softmax回归 损失函数 图片分类数据集 Softmax回归从零开始实现 Softmax回归简洁实现 Softmax回归 回归和分类的区别 回归问题举例上节课的预测房价问题,分类问题就是对样本进行分类 回归和分类的具体区别 假设真实的类别为第i个类别(值为1&#x…...

git 初始化项目并上传到github
如果还没配置过,需要配置账号信息 git config --global user.name "baymax-collab" git config --global user.email "baymax-collabtest.com"创建一个新的存储库 git clone gitgithub.com:xxxx cd test git switch --create main touch READ…...
前端javascript的DOM对象操作技巧,全场景解析
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 所属的专栏:前端泛海 景天的主页:景天科技苑 文章目录 1.js的DOM介绍2.节点元素层级关系3.通过js修改,清空节点…...
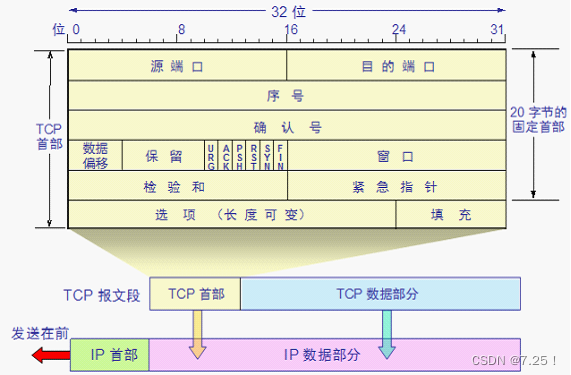
TCP包头、TCP为什么安全可靠、UDP和TCP的区别、http协议
我要成为嵌入式高手之3月8日Linux高编第十八天!! __________________________________________________ 学习笔记 TPC包头 1、序号 发送端发送数据包的编号 2、确认号 已经确认接收到的数据的编号,只有当ACK为1时,该位才有用 …...
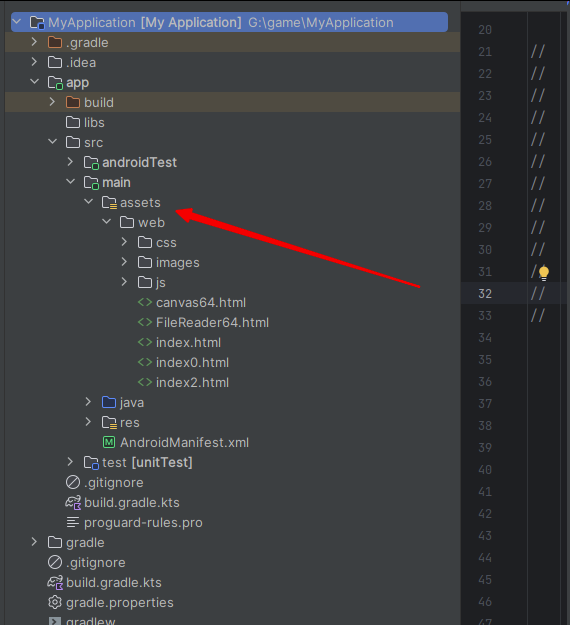
Android使用WebView打开内嵌H5网页
Android打开外部网页链接请参考上一篇文章 https://public.blog.csdn.net/article/details/136384559 继上篇,新建assets文章夹,将H5的网页资源放到此文件夹下 把H5的资源文件都拷进来 这个时候,将添加打开本地网页的代码: //打…...
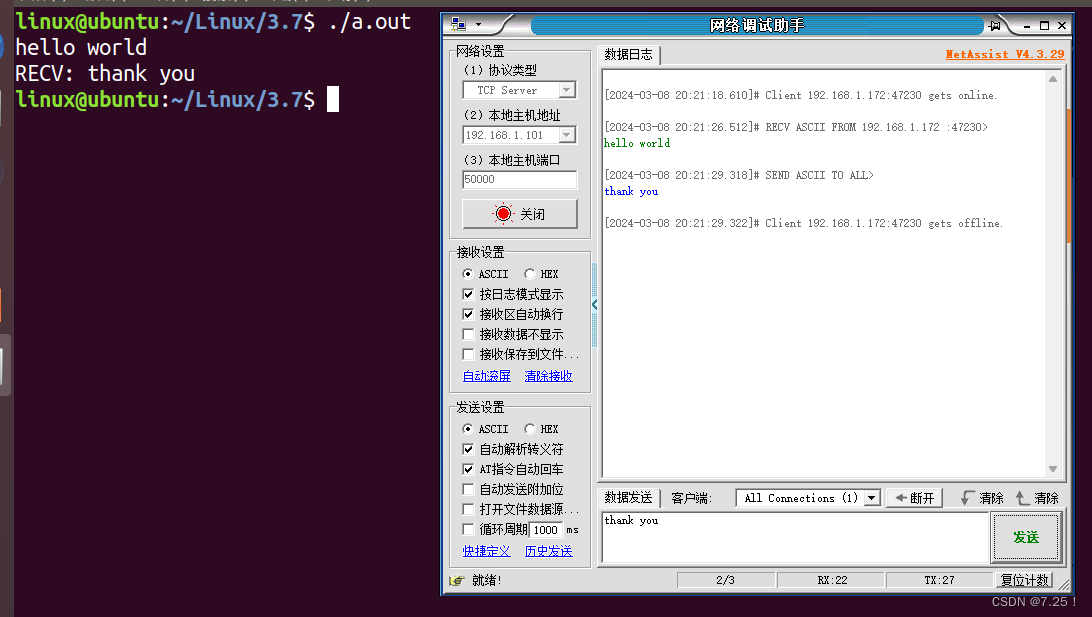
UDP实现文件的发送、UDP实现全双工的聊天、TCP通信协议
我要成为嵌入式高手之3月7日Linux高编第十七天!! ———————————————————————————— 回顾 重要程序 1、UDP实现文件的发送 发端: #include "head.h"int main(void) {int sockfd 0;struct sockaddr_i…...

Yocto - Project Quick Build
欢迎光临! 这篇简短的文档将向您介绍使用 Yocto 项目构建典型镜像的过程。本文还介绍了如何为特定硬件配置构建。您将使用 Yocto Project 构建一个名为 Poky 的参考嵌入式操作系统。 Welcome! This short document steps you through the process for a typical i…...
)
深入探讨C++中的可变参数列表(Variadic Templates)
文章目录 导言可变参数列表的基本用法使用std::initializer_list应用场景 导言 在C编程中,处理可变数量参数的能力是一种非常有用的功能。通过可变参数列表,你可以编写更加通用和灵活的函数,从而提高代码的可读性和重用性。本文将详细介绍C中…...

MS2548 国产自动方向控制、半双工 RS-485 收发器 替代MAX13487
MS2548 国产自动方向控制、半双工 RS-485 收发器 替代MAX13487 北京冠宇铭通科技有限公司 肖小姐 产品简述 MS2548 是一个 5V 供电、半双工 RS-485 收发器。 芯片具有自动换向控制功能,可用于隔离485 端口,驱动器输入与使能信号一起配合控制芯片的状态&…...
数据库大师之路:Oracle在线学习平台全指南!
介绍数据库是由甲骨文公司开发的一款关系数据库管理系统(RDBMS),在数据库领域具有领先地位,并且以其系统可移植性而闻名。以下是对Oracle数据库的详细介绍: 市场地位:Oracle数据库是目前世界上流行的关系数…...
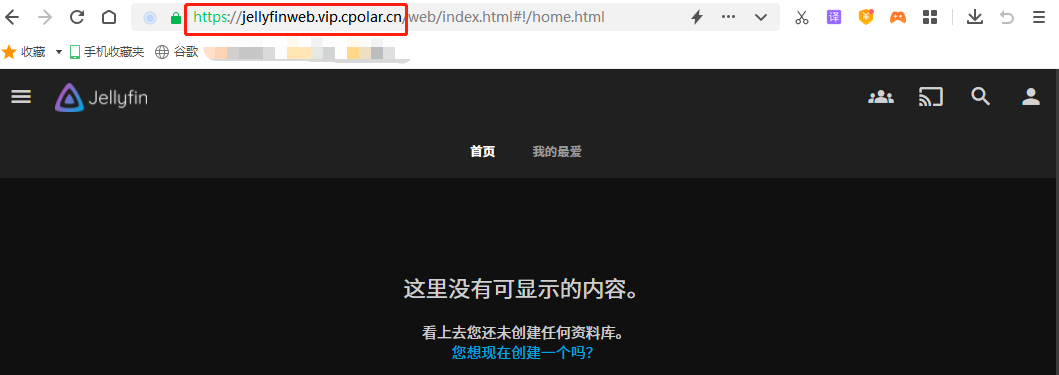
如何在Windows系统部署Jellyfin Server并实现公网访问内网影音文件
文章目录 1. 前言2. Jellyfin服务网站搭建2.1. Jellyfin下载和安装2.2. Jellyfin网页测试 3.本地网页发布3.1 cpolar的安装和注册3.2 Cpolar云端设置3.3 Cpolar本地设置 4.公网访问测试5. 结语 1. 前言 随着移动智能设备的普及,各种各样的使用需求也被开发出来&…...
CORBA协议开发)
华为北向网管NCE开发教程(3)CORBA协议开发
华为北向网管NCE开发教程(1)闭坑选接口协议 华为北向网管NCE开发教程(2)REST接口开发 华为北向网管NCE开发教程(3)CORBA协议开发 如果你真的还有选择的余地,能用REST,尽量用REST&…...
)
【算法训练营】最长公共子序列,倒水问题,奶牛吃草(Python实现)
最长公共子序列 时间限制:1 sec 空间限制:256 MB 问题描述 给定两个 1 到 n 的排列 A,B (即长度为 n 的序列,其中 [1,n] 之间的所有数都出现了恰好一次)。 求它们的最长公共子序列长度。 输入格式 第一行一个整数 n &a…...

Armadillo:矩阵类、向量类、Cube类和泛型类
文章目录 矩阵类、向量类、Cube类和泛型类Mat<type>matcx_matCol<type>veccx_vecRow<type>rowveccx_rowvecCube<type>cubecx_cubefield<object_type>SpMat<type>sp_matsp_cx_mat运算符: − * % / ! < > <…...

【守护健康】小脑萎缩患者必备营养指南
当生活给予我们挑战,我们选择用科学和关爱予以回应。面对小脑萎缩这一难题,正确的营养补充不仅是一剂强心针,更是患者康复之路上的坚实伙伴。今天,让我们一起了解那些能够助力小脑萎缩患者的神奇维生素! 1. 维生素B群…...
lvs集群中NAT模式
群集的含义 由多台主机构成,但对外表现为一个整体,只提供一个访问入口,相当于一台大型的计算机。 横向发展:放更多的服务器,有调度分配的问题。 垂直发展:升级单机的硬件设备,提高单个服务器自身功能。 …...
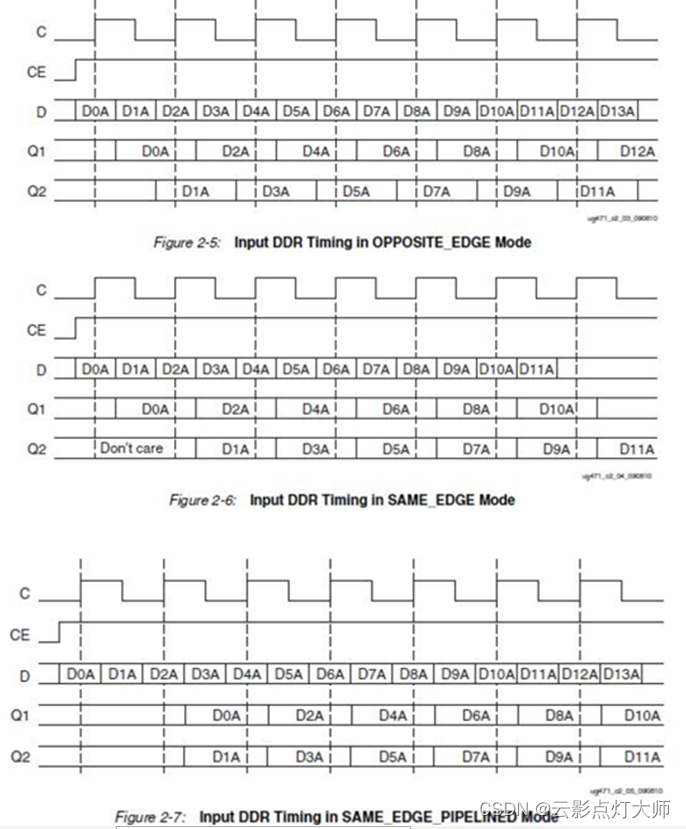
FPGA——三速自适应以太网设计(2)GMII与RGMII接口
FPGA——以太网设计(2)GMII与RGMII 基础知识(1)GMII(2)RGMII(3)IDDR GMII设计转RGMII接口跨时钟传输模块 基础知识 (1)GMII GMII:发送端时钟由MAC端提供 下…...
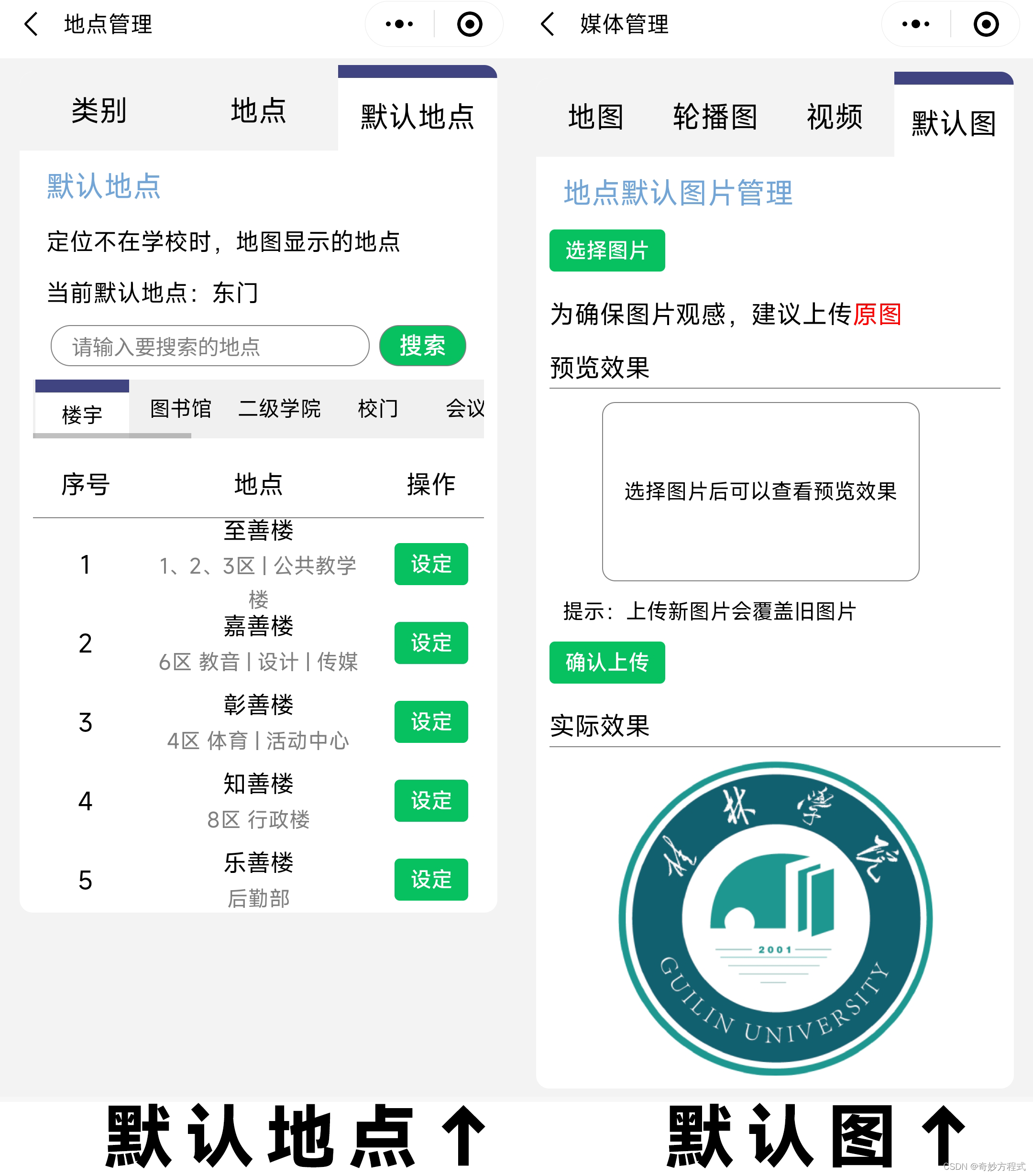
【校园导航小程序】2.0版本 静态/云开发项目 升级日志
演示视频 【校园导航小程序】2.0版本 静态/云开发项目 演示 首页 重做了首页,界面更加高效和美观 校园指南页 新增了 “校园指南” 功能,可以搜索和浏览校园生活指南 地图页 ①弃用路线规划插件,改用SDK开发包。可以无阻通过审核并发布…...
)
深入揭秘Lucene:全面解析其原理与应用场景(二)
本系列文章简介: 本系列文章将深入揭秘Lucene,全面解析其原理与应用场景。我们将从Lucene的基本概念和核心组件开始,逐步介绍Lucene的索引原理、搜索算法以及性能优化策略。通过阅读本文,读者将会对Lucene的工作原理有更深入的了解…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
