06分支限界法
文章目录
- 八数码难题
- 普通BFS算法
- 全局择优算法(A算法,启发式搜索算法)
- 单源最短路径问题
- 装载问题
- 算法思想:队列式分支限界法
- 优先队列式分支限界法
- 布线问题
- 最大团问题
- 批处理作业调度问题
分支限界法与回溯法的区别:
(1)求解目标不同:回溯法的求解目标是找出解空间树中满足约束条件的所有解,而分支限界法的求解目标则是找出满足约束条件的一个解,或是在满足约束条件的解中找出在某种意义下的最优解。
(2)搜索方式的不同:回溯法以深度优先的方式搜索解空间树,而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间树。
BFS框架:queue.add(起点);
while(队列不为空)
{ 取出队首点;if(如果达到目标) 结束 for(当前结点可拓展选择) {if (判重检测通过)queue.add(新扩展结点);}
}
常见的两种分支限界法
(1)队列式(FIFO)分支限界法
按照队列先进先出(FIFO)原则选取下一个节点为扩展节点。
(2)优先队列式分支限界法
按照优先队列中规定的优先级选取优先级最高的节点成为当前扩展节点。

八数码难题
在 3*3 的方格棋盘上,分别放置了标有数字1、2、3、4、5、6、7、8的八张牌,初始状态S0,目标状态Sg。
可以使用的操作有:空格左移,空格上移,空格右移,空格下移即只允许把位于空格左、上、右、下方的牌移入空格,寻找从初始状态到目标状态的移动棋子步数最少的解路径。
普通BFS算法
1 从初始布局出发,先把移动一步后的布局全部找出,检查是否有目标布局,若有一定是最少移动步骤;
2 若没有,再从这些一步的布局出发,找到移动两步后的所有布局;再检查是否有目标布局。若有一定是最少移动步骤;如此继续,直到找到目标布局。
3 由于是按移动步数从少到多产生布局的,所以,找到的第一个目标布局一定是最少步骤的。

全局择优算法(A算法,启发式搜索算法)
设估价函数为: f(n)=d(n)+W(n)
其中,d(n)表示节点 n 在搜索树中的深度;
w(n)表示节点 n 中“不在位”的数码个数。
一般来说,某节点中的“不在位”的数码个数越多,说明它离目标节点越远。
对初始节点 S0,由于 d(S0)= 0,W(S0)= 3, 因此有 f(S0)=0+3=3

单源最短路径问题
问题描述:在下图所给的有向图G中,每一边都有一个非负边权。要求图G的从源顶点s到目标顶点t之间的最短路径。
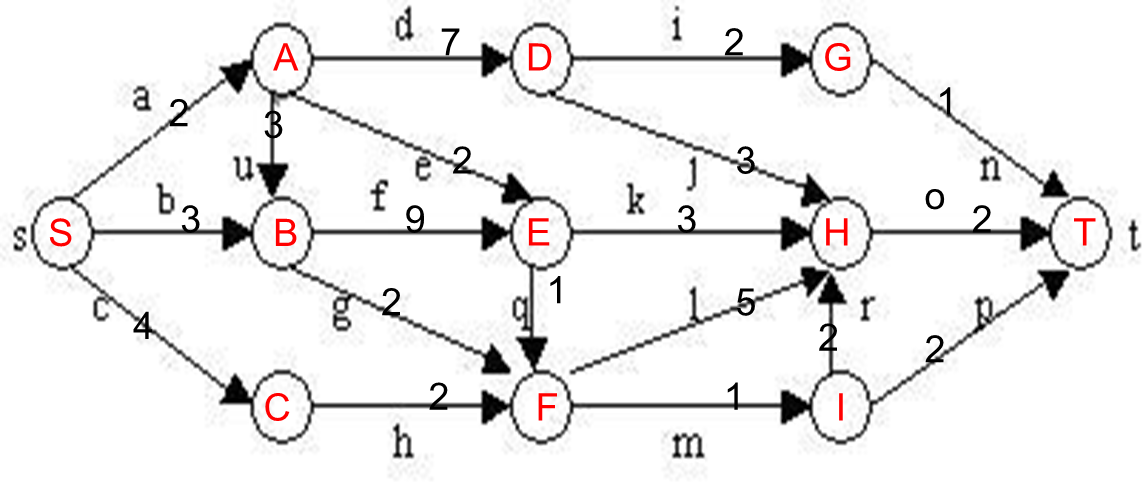

算法思想:
算法从图G的源顶点s和空优先队列开始。结点s被扩展后,它的儿子结点被依次插入堆中。
此后,算法从极小堆中取出具有最小当前路长的结点作为当前扩展结点,并依次检查与当前扩展结点相邻的所有顶点。
如果从当前扩展结点i到顶点j有边可达,且从源出发,途经顶点i再到顶点j的所相应的路径的长度小于当前最优路径长度,则将该顶点作为活结点插入到活结点优先队列中。
这个结点的扩展过程一直继续到活结点优先队列为空时为止。
剪枝策略:
在算法扩展结点的过程中,一旦发现一个结点的下界不小于当前找到的最短路长,则算法剪去以该结点为根的子树。在算法中,利用结点间的控制关系进行剪枝。从源顶点s出发,2条不同路径到达图G的同一顶点。由于两条路径的路长不同,因此可以将路长长的路径所对应的树中的结点为根的子树剪去。
装载问题
问题描述:有一批共n个集装箱要装上2艘载重量分别为C1和C2的轮船,其中集装箱i的重量为Wi,且满足下列条件,装载问题要求确定是否有一个合理的装载方案可将这个集装箱装上这2艘轮船。如果有,找出一种装载方案。 实质就是要求第1艘船的最优装载。
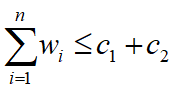
算法思想:队列式分支限界法
在算法的while循环中,首先检测当前扩展结点的左儿子结点是否为可行结点。如果是则将其加入到活结点队列中。然后将其右儿子结点加入到活结点队列中(右儿子结点一定是可行结点)。2个儿子结点都产生后,当前扩展结点被舍弃。
活结点队列中的队首元素被取出作为当前扩展结点,由于队列中每一层结点之后都有一个尾部标记-1,故在取队首元素时,活结点队列一定不空。当取出的元素是-1时,再判断当前队列是否为空。如果队列非空,则将尾部标记-1加入活结点队列,算法开始处理下一层的活结点。
while (true) {// 检查左儿子结点if (Ew + w[i] <= c) // x[i] = 1,Ew表示当前扩展结点相应的重量EnQueue(Q, Ew + w[i], bestw, i, n); //将活结点加入活结点队列// 右儿子结点总是可行的,直接加入EnQueue(Q, Ew, bestw, i, n); // x[i] = 0Q.Delete(Ew); // 取下一扩展结点if (Ew == -1) { // 同层结点尾部if (Q.IsEmpty()) return bestw;Q.Add(-1); // 同层结点尾部标志Q.Delete(Ew); // 取下一扩展结点i++;} // 进入下一层 } }算法的改进
节点的左子树表示将此集装箱装上船,右子树表示不将此集装箱装上船。
设bestw是当前最优解;ew是当前扩展结点所相应的重量;r是剩余集装箱的重量。则当ew+r<=bestw时,可将其右子树剪去,因为该子树不可能产生更优解。
另外,为了确保右子树成功剪枝,应该在算法每一次进入左子树的时候更新bestw的值。
算法的改进// 检查左儿子结点Type wt = Ew + w[i]; // 左儿子结点的重量if (wt <= c) { // 可行结点if (wt > bestw) bestw = wt;// 加入活结点队列if (i < n) Q.Add(wt);
}
// 检查右儿子结点if (Ew + r > bestw && i < n)Q.Add(Ew); // 可能含最优解Q.Delete(Ew); // 取下一扩展结点构造最优解
为了在算法结束后能方便地构造出与最优值相应的最优解,算法必须存储相应子集树中从活结点到根结点的路径。为此目的,可在每个结点处设置指向其父结点的指针,并设置左、右儿子标志。
class QNode{ QNode *parent; // 指向父结点的指针bool LChild; // 左儿子标志Type weight; // 结点所相应的载重量
};找到最优值后,可以根据parent回溯到根节点,找到最优解。// 构造当前最优解
for (int j = n - 1; j > 0; j--) {bestx[j] = bestE->LChild; //被选中的集装箱 bestE = bestE->parent; //回溯到该路径中的上层结点
}优先队列式分支限界法
算法思想:
解装载问题的优先队列式分支限界法用最大优先队列存储活结点表。活结点x在优先队列中的优先级定义为从根结点到结点x的路径所相应的载重量再加上剩余集装箱的重量之和。
优先队列中优先级最大的活结点成为下一个扩展结点。以结点x为根的子树中所有结点相应的路径的载重量不超过它的优先级。子集树中叶结点所相应的载重量与其优先级相同。在优先队列式分支限界法中,一旦有一个叶结点成为当前扩展结点,则可以断言该叶结点所相应的解即为最优解。此时可终止算法。
布线问题

算法思想:队列式分支限界法
求解方法:
(1)起始位置a第一个扩展;
(2)依次考虑距a距离为1、2、3、…、的方格,并作标记,并存入活结点队列;
(3)从活结点队列取结点扩展,一直搜索到目标方格b或活结点队列为空时为止。

二维数组 grid[i][j]:表示方格阵列
初始时,
grid[i][j]= 0:该方格允许布线
grid[i][j]= 1:该方格被封锁,不允许布线
边界处理:四周用方格阵列围起来,作为处理的边界。
for (int i = 0; i <= m + 1; i++) { grid[0][i] = grid[n + 1][i] = 1; } //顶部和底部
for (int i = 0; i <= n + 1; i++) { grid[i][0] = grid[i][m + 1] = 1; } //左翼和右翼方格的方位offset,沿四个方向的移动分别记为offset[0]~offset[3]Position offset[4]; //offset是四个移动方向的相对位移矩阵
offset[0].row = 0; offset[0].col = 1; // 右
offset[1].row = 1; offset[1].col = 0; // 下
offset[2].row = 0; offset[2].col = -1; // 左
offset[3].row = -1; offset[3].col = 0; // 上算法将起始距离标记为2(因0,1用于表示状态)
grid[start.row][start.col] = 2; //起始点距离为2
here.row = start.row; // here为正在布线的方格,初始值为start。
here.col = start.col; do { // 标记可达相邻方格for (int i = 0; i < NumOfNbrs; i++){ // NumOfNbrs为相邻方格数nbr.row = here.row + offset[i].row; // here是正在走线的方格,nbr.col = here.col + offset[i].col; nbr是可考虑走线方格if (grid[nbr.row][nbr.col] == 0) { // 该方格未标记grid[nbr.row][nbr.col] = grid[here.row][here.col] + 1;// grid[][]中记录该方格距离起始方格距离if ((nbr.row == finish.row) && (nbr.col == finish.col)) break; // 完成布线Q.Add(nbr);} //队列中加入新的扩展结点}
}
找到目标位置后,可以通过回溯方法找到这条最短路径。
构造最短路径:
从终点finish出发,开始向起始方格方向回溯。
每次向标记距离比当前方格标记距离少1的相邻方格移动,直至到达起始方格时为止。搜索时,比较相邻4个方格的标号。
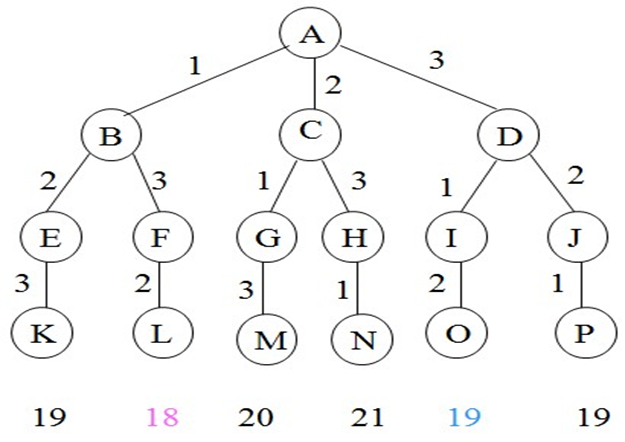
最大团问题
给定无向图G=(V,E)。如果U∈V,且对任意u,v∈U有(u,v)∈E,则称U是G的完全子图。
G的完全子图U是G的团当且仅当U不包含在G的更大的完全子图中。G的最大团是指G中所含顶点数最多的团。
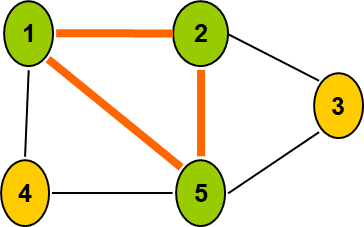
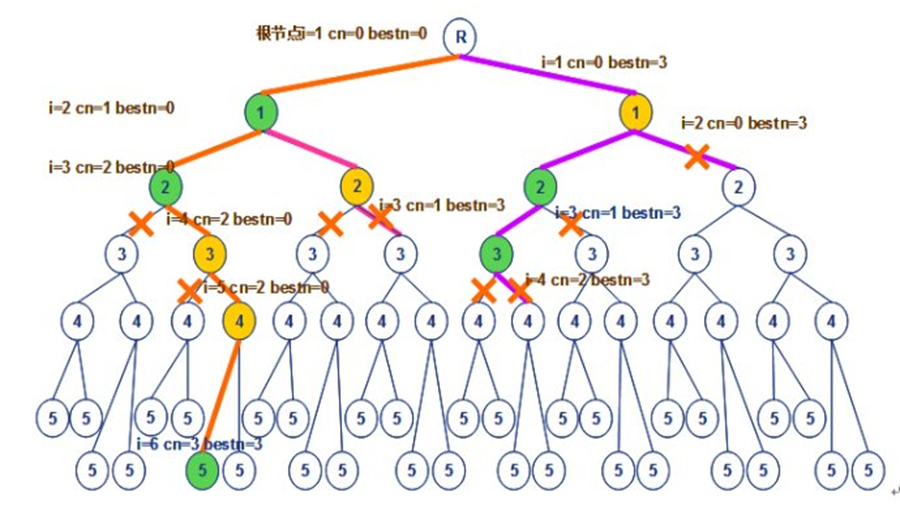
上界函数
用变量cliqueSize表示与该结点相应的团的顶点数;
level表示结点在子集空间树中所处的层次;
用cliqueSize +n-level+1作为顶点数上界upperSize的值。
在此优先队列式分支限界法中,upperSize实际上也是优先队列中元素的优先级。
算法总是从活结点优先队列中抽取具有最大upperSize值的元素作为下一个扩展元素。
算法思想
子集树的根结点是初始扩展结点,对于这个特殊的扩展结点,其cliqueSize的值为0。 算法在扩展内部结点时,首先考察其左儿子结点。在左儿子结点处,将顶点i加入到当前团中,并检查该顶点与当前团中其它顶点之间是否有边相连。当顶点i与当前团中所有顶点之间都有边相连,则相应的左儿子结点是可行结点,将它加入到子集树中并插入活结点优先队列,否则就不是可行结点。接着继续考察当前扩展结点的右儿子结点。当upperSize>bestn时,右子树中可能含有最优解,此时将右儿子结点加入到子集树中并插入到活结点优先队列中。算法的while循环的终止条件是遇到子集树中的一个叶结点(即n+1层结点)成为当前扩展结点。
批处理作业调度问题
给定n个作业的集合J={J1,J2,…,Jn}。每一个作业Ji都有2项任务要分别在2台机器上完成。每一个作业必须先由机器1处理,然后再由机器2处理。
作业Ji需要机器j的处理时间为tji,i=1,2,…,n;j=1,2。
对于一个确定的作业调度,设是Fji是作业i在机器j上完成处理的时间。
则所有作业在机器2上完成处理的时间和称为该作业调度的完成时间和。
批处理作业调度问题要求对于给定的n个作业,制定最佳作业调度方案,使其完成时间和达到最小。
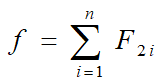


相关文章:

06分支限界法
文章目录八数码难题普通BFS算法全局择优算法(A算法,启发式搜索算法)单源最短路径问题装载问题算法思想:队列式分支限界法优先队列式分支限界法布线问题最大团问题批处理作业调度问题分支限界法与回溯法的区别: &#x…...

Docker Compose编排
一、概念1、Docker Compose是什么Docker Compose的前身是Fig,它是一个定义及运行多个Docker容器的工具通过 Compose,不需要使用shell脚本来启动容器,而使用 YAML 文件来配置应用程序需要的所有服务然后使用一个命令,根据 YAML 的文…...

Docker进阶 - 11. Docker Compose 编排服务
注:本文只对一些重要步骤和yml文件进行一些讲解,其他的具体程序没有记录。 目录 1. 原始的微服务工程编排(不使用Compose) 2. 使用Compose编排微服务 2.1 编写 docker-compose.yml 文件 2.2 修改并构建微服务工程镜像 2.3 启动 docker-compose 服务…...
)
福利篇2——嵌入式岗位笔试面试资料汇总(含大厂笔试面试真题)
前言 汇总嵌入式软件岗位笔试面试资料,供参考。 文章目录 前言一、公司嵌入式面经1、小米1)面试时长2)面试问题2、科大讯飞1)面试时长2)面试题目3、其余公司面经二、嵌入式笔试面试资料(全)三、嵌入式岗位薪资报告四、硬件岗位薪资报告一、公司嵌入式面经 1、小米 1)…...

[ubuntu]LVM磁盘管理
LVM是 Logical Volume Manager(逻辑卷管理)的简写,是Linux环境下对磁盘分区进行管理的一种机制,由Heinz Mauelshagen在Linux 2.4内核上实现。LVM可以实现用户在无需停机的情况下动态调整各个分区大小。1.简介 LVM本质上是一个…...

开源流程引擎Camunda
开源流程引擎Camunda 文章作者:智星 1.简介 Camunda是一个轻量级的商业流程开源平台,是一种基于Java的框架,持久层采用Mybatis,可以内嵌集成到Java应用、SpringBooot应用中,也可以独立运行,其支持BPMN&a…...
)
【PTA Advanced】1155 Heap Paths(C++)
目录 题目 Input Specification: Output Specification: Sample Input 1: Sample Output 1: Sample Input 2: Sample Output 2: Sample Input 3: Sample Output 3: 思路 代码 题目 In computer science, a heap is a specialized tree-based data structure that s…...
)
Educational Codeforces Round 129 (Rated for Div. 2)
A. Game with Cards. 题目链接 题目大意: Alice和Bob玩卡牌。Alice有n张,Bob有m张。第一轮选手出一张数字卡牌。第二轮另一个选手要选择一张比他大的,依此类推。谁没有牌可出则输。问Alice和Bob分别先手时,谁赢?输出…...

[数据库]表的增删改查
●🧑个人主页:你帅你先说. ●📃欢迎点赞👍关注💡收藏💖 ●📖既选择了远方,便只顾风雨兼程。 ●🤟欢迎大家有问题随时私信我! ●🧐版权:本文由[你帅…...

分享77个JS菜单导航,总有一款适合您
分享77个JS菜单导航,总有一款适合您 77个JS菜单导航下载链接:https://pan.baidu.com/s/1e_384_1KC2oSTDy7AaD3og?pwdzkw6 提取码:zkw6 Python采集代码下载链接:https://wwgn.lanzoul.com/iKGwb0kye3wj class ChinaZJsSeleni…...
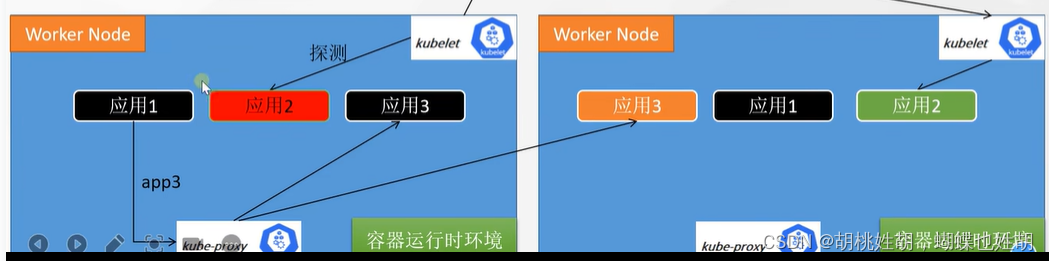
kubernetes -- 核心组件介绍以及组件的运行流程
常用组件大白话说 如果想要官方的,详细的信息,请看官方文档。 https://kubernetes.io/zh-cn/docs/concepts/overview/components/ 现在介绍一些核心的概念: etcd:存储所有节点的信息,节点上部署的容器信息等都存在数…...

微信小程序Springboot短视频分享系统
3.1小程序端 用户注册页面,输入用户的个人信息点击注册即可。 注册完成后会返回到登录页面,用户输入自己注册的账号密码即可登录成功 登录成功后我们可以看到有相关的视频还有视频信息,我的信息等。 视频信息推荐是按照点击次数进行推荐的&am…...

排序算法学习
文章目录前言一、直接插入排序算法二、折半插入排序算法三、2路插入排序算法四、快速排序算法学习前言 算法是道路生涯的一个巨大阻碍。今日前来解决这其中之一:有关的排序算法,进行实现以及性能分析。 一、直接插入排序算法 插入排序算法实现主要思想…...
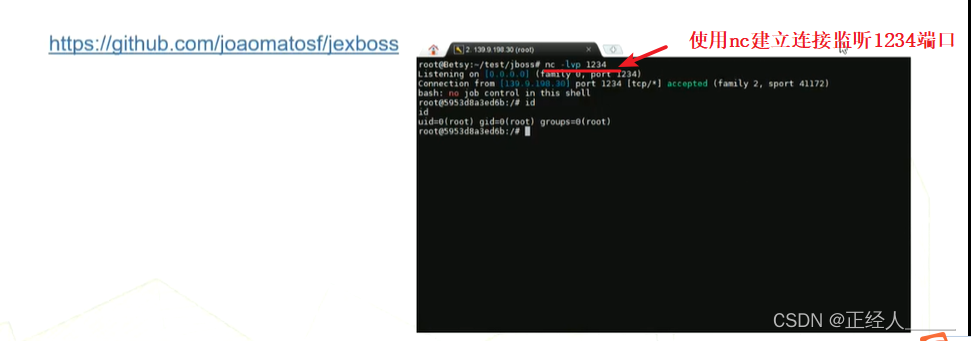
常见漏洞之 struts2+ jboss
数据来源 本文仅用于信息安全的学习,请遵守相关法律法规,严禁用于非法途径。若观众因此作出任何危害网络安全的行为,后果自负,与本人无关。 01 Struts2相关介绍 》Struts2概述 》Struts2历史漏洞(1) 》…...

leetcode470 用Rand7()实现Rand10()
力扣470 第一步:根据Rand7()函数制作一个可以随机等概率生成0和1的函数rand_0and1 调用Rand7()函数,随机等概率生成1,2,3,4,5,6,7 这时我们设置:生成1,2&a…...

JSON数据解析商品详情API
大家有探讨稳定获取商品主图、jiage、标题,及sku的完整解决方案。这个引起了我技术挑战的兴趣,然后各种网上资料查询,最终还是不负努力,找到更好的解决方案,不再出现任何滑块验证码,完全绕过,实…...

服务端开发Java面试复盘篇1
上周投了一些简历,约了8-9家面试,其中完成了3家的第一轮面试,由于面试的是Java 的实习生,感觉问的题目都比较基础,不过有些问题回答的不是很好,在这里对回答的不太好的题目做一下总结和复盘。 目录 一、后…...

Android框架WiFi架构
同学,别退出呀,我可是全网最牛逼的 WIFI/BT/GPS/NFC分析博主,我写了上百篇文章,请点击下面了解本专栏,进入本博主主页看看再走呗,一定不会让你后悔的,记得一定要去看主页置顶文章哦。 一、wpa_supplicant:wpa_supplicant本身开源项目源码,被谷歌收购之后加入Android移…...

rt-thread 移植调试记录
rt-thread 移植调试记录 记录rt-thread移植的过程。这里移植仅仅是利用rt-thread源码目录已经移植好的文件,组建自己的工程,不需要自己编写汇编完成底层移植。 1. 搭建基础工程 这里使用的是正点原子的潘多拉开发板,MCU为stm32l475。需要先…...

红外线额温枪与红外线温度传感器的原理分析
额温枪主要针对测量人体额温基准而设计,使用也非常简单方便。测体温可以达到一秒即可准确测量。并且不需要接触人体,隔着空气即可一键测温。非常适合家庭、学校、企业等场所。 但是由于其精度原因(一般为 0.2 ℃,也有更低的&#…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
