双周赛99(贪心、数学、区间合并计算、换根DP)
文章目录
- 双周赛99
- [6312. 最小和分割](https://leetcode.cn/problems/split-with-minimum-sum/)
- 贪心
- [6311. 统计染色格子数](https://leetcode.cn/problems/count-total-number-of-colored-cells/)
- 找规律
- [6313. 统计将重叠区间合并成组的方案数](https://leetcode.cn/problems/count-ways-to-group-overlapping-ranges/)
- 相似:[56. 合并区间](https://leetcode.cn/problems/merge-intervals/)
- [6314. 统计可能的树根数目](https://leetcode.cn/problems/count-number-of-possible-root-nodes/)
- 换根DP
双周赛99
6312. 最小和分割
难度简单4
给你一个正整数 num ,请你将它分割成两个非负整数 num1 和 num2 ,满足:
-
num1和
num2直接连起来,得到
num各数位的一个排列。
- 换句话说,
num1和num2中所有数字出现的次数之和等于num中所有数字出现的次数。
- 换句话说,
-
num1和num2可以包含前导 0 。
请你返回 num1 和 num2 可以得到的和的 最小 值。
注意:
num保证没有前导 0 。num1和num2中数位顺序可以与num中数位顺序不同。
示例 1:
输入:num = 4325
输出:59
解释:我们可以将 4325 分割成 num1 = 24 和 num2 = 35 ,和为 59 ,59 是最小和。
示例 2:
输入:num = 687
输出:75
解释:我们可以将 687 分割成 num1 = 68 和 num2 = 7 ,和为最优值 75 。
提示:
10 <= num <= 109
贪心
class Solution {// 思考 1:越高位的数字对结果的影响越大,所以优先排列最小的数字;// 思考 2:如果划分两个数字的长度不均,会放大最终的值;// 算法:对数字排序,从小到大分别排列到两个数字上。public int splitNum(int num) {char[] arr = (num + "").toCharArray();Arrays.sort(arr);int[] res = new int[2];for(int i = 0; i < arr.length; i++){res[i % 2] = res[i % 2] * 10 + (int)arr[i]-'0';}return res[0] + res[1];}
}
6311. 统计染色格子数
难度中等2
有一个无穷大的二维网格图,一开始所有格子都未染色。给你一个正整数 n ,表示你需要执行以下步骤 n 分钟:
- 第一分钟,将 任一 格子染成蓝色。
- 之后的每一分钟,将与蓝色格子相邻的 所有 未染色格子染成蓝色。
下图分别是 1、2、3 分钟后的网格图。
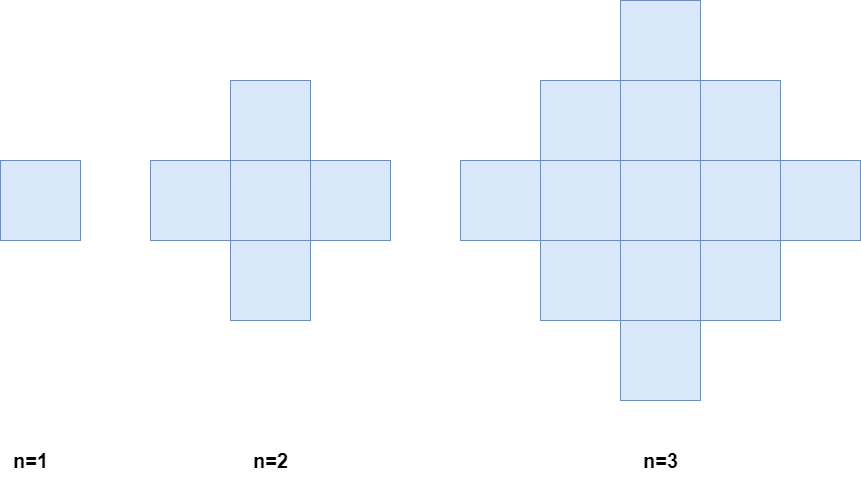
请你返回 n 分钟之后 被染色的格子 数目。
示例 1:
输入:n = 1
输出:1
解释:1 分钟后,只有 1 个蓝色的格子,所以返回 1 。
示例 2:
输入:n = 2
输出:5
解释:2 分钟后,有 4 个在边缘的蓝色格子和 1 个在中间的蓝色格子,所以返回 5 。
提示:
1 <= n <= 105
找规律
class Solution {// 斜着看其实就是n * n大小的方阵空隙里夹了一个 (n - 1) * (n - 1)的方阵public long coloredCells(int n) {// dp[1] = 1 1x1// dp[2] = 5 2x2 + 1// dp[3] = 13 3x3 + 4// int[] dp = new int[n+1];// dp[1] = 1;// for(int i = 2; i <= n; i++){// dp[i] = i * i + (i-1) * (i-1);// }// return dp[n];long a = n;return a * a + (a-1) * (a-1);}
}
6313. 统计将重叠区间合并成组的方案数
难度中等8
给你一个二维整数数组 ranges ,其中 ranges[i] = [starti, endi] 表示 starti 到 endi 之间(包括二者)的所有整数都包含在第 i 个区间中。
你需要将 ranges 分成 两个 组(可以为空),满足:
- 每个区间只属于一个组。
- 两个有 交集 的区间必须在 同一个 组内。
如果两个区间有至少 一个 公共整数,那么这两个区间是 有交集 的。
- 比方说,区间
[1, 3]和[2, 5]有交集,因为2和3在两个区间中都被包含。
请你返回将 ranges 划分成两个组的 总方案数 。由于答案可能很大,将它对 109 + 7 取余 后返回。
示例 1:
输入:ranges = [[6,10],[5,15]]
输出:2
解释:
两个区间有交集,所以它们必须在同一个组内。
所以有两种方案:
- 将两个区间都放在第 1 个组中。
- 将两个区间都放在第 2 个组中。
示例 2:
输入:ranges = [[1,3],[10,20],[2,5],[4,8]]
输出:4
解释:
区间 [1,3] 和 [2,5] 有交集,所以它们必须在同一个组中。
同理,区间 [2,5] 和 [4,8] 也有交集,所以它们也必须在同一个组中。
所以总共有 4 种分组方案:
- 所有区间都在第 1 组。
- 所有区间都在第 2 组。
- 区间 [1,3] ,[2,5] 和 [4,8] 在第 1 个组中,[10,20] 在第 2 个组中。
- 区间 [1,3] ,[2,5] 和 [4,8] 在第 2 个组中,[10,20] 在第 1 个组中。
提示:
1 <= ranges.length <= 105ranges[i].length == 20 <= starti <= endi <= 109
class Solution {//假设最后分成了 m 个集合,那么每个集合都可以决定要在第一个组还是第二个组,// 所以方案数为 2 ^ mprivate static final int MOD = (int)1e9 + 7;public int countWays(int[][] ranges) {Arrays.sort(ranges, (a,b) -> a[0] == b[0] ? a[1]-b[1] : a[0] - b[0]);int ans = 2;int maxR = ranges[0][1];for(int[] p : ranges){if(p[0] > maxR){ // 产生了新的集合 m加一ans = ans * 2 % MOD;}maxR = Math.max(maxR, p[1]);}return ans;}
}
相似:56. 合并区间
难度中等1815
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 104intervals[i].length == 20 <= starti <= endi <= 104
class Solution {public int[][] merge(int[][] intervals) {Arrays.sort(intervals, (a, b) -> a[0] == b[0] ? a[1]-b[1] : a[0]-b[0]);List<int[]> list = new ArrayList<>();int i = 0;while(i < intervals.length){int left = intervals[i][0];int right = intervals[i][1];while(i+1 < intervals.length && right >= intervals[i+1][0]){right = Math.max(right, intervals[i+1][1]);i++;}list.add(new int[]{left, right});i++;}int[][] res = new int[list.size()][2];for(int k = 0; k < list.size(); k++){res[k] = list.get(k);}return res;}
}
6314. 统计可能的树根数目
难度困难13
Alice 有一棵 n 个节点的树,节点编号为 0 到 n - 1 。树用一个长度为 n - 1 的二维整数数组 edges 表示,其中 edges[i] = [ai, bi] ,表示树中节点 ai 和 bi 之间有一条边。
Alice 想要 Bob 找到这棵树的根。她允许 Bob 对这棵树进行若干次 猜测 。每一次猜测,Bob 做如下事情:
- 选择两个 不相等 的整数
u和v,且树中必须存在边[u, v]。 - Bob 猜测树中
u是v的 父节点 。
Bob 的猜测用二维整数数组 guesses 表示,其中 guesses[j] = [uj, vj] 表示 Bob 猜 uj 是 vj 的父节点。
Alice 非常懒,她不想逐个回答 Bob 的猜测,只告诉 Bob 这些猜测里面 至少 有 k 个猜测的结果为 true 。
给你二维整数数组 edges ,Bob 的所有猜测和整数 k ,请你返回可能成为树根的 节点数目 。如果没有这样的树,则返回 0。
示例 1:
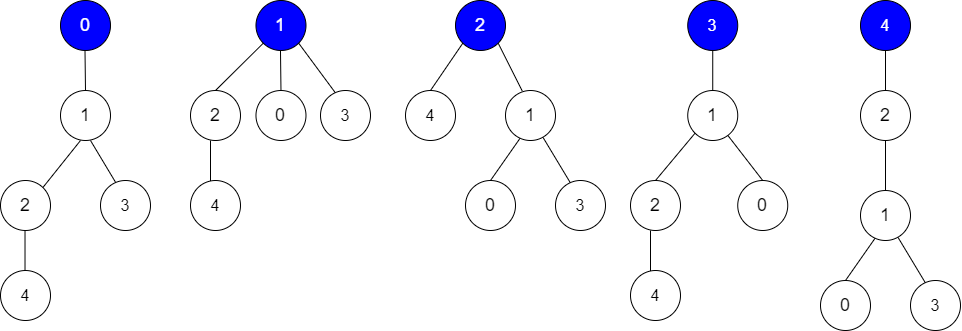
输入:edges = [[0,1],[1,2],[1,3],[4,2]], guesses = [[1,3],[0,1],[1,0],[2,4]], k = 3
输出:3
解释:
根为节点 0 ,正确的猜测为 [1,3], [0,1], [2,4]
根为节点 1 ,正确的猜测为 [1,3], [1,0], [2,4]
根为节点 2 ,正确的猜测为 [1,3], [1,0], [2,4]
根为节点 3 ,正确的猜测为 [1,0], [2,4]
根为节点 4 ,正确的猜测为 [1,3], [1,0]
节点 0 ,1 或 2 为根时,可以得到 3 个正确的猜测。
示例 2:
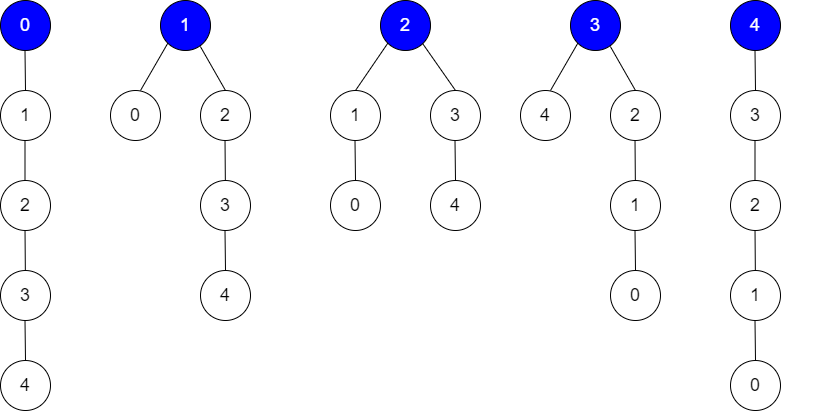
输入:edges = [[0,1],[1,2],[2,3],[3,4]], guesses = [[1,0],[3,4],[2,1],[3,2]], k = 1
输出:5
解释:
根为节点 0 ,正确的猜测为 [3,4]
根为节点 1 ,正确的猜测为 [1,0], [3,4]
根为节点 2 ,正确的猜测为 [1,0], [2,1], [3,4]
根为节点 3 ,正确的猜测为 [1,0], [2,1], [3,2], [3,4]
根为节点 4 ,正确的猜测为 [1,0], [2,1], [3,2]
任何节点为根,都至少有 1 个正确的猜测。
提示:
edges.length == n - 12 <= n <= 1051 <= guesses.length <= 1050 <= ai, bi, uj, vj <= n - 1ai != biuj != vjedges表示一棵有效的树。guesses[j]是树中的一条边。0 <= k <= guesses.length
换根DP
题解:https://leetcode.cn/problems/count-number-of-possible-root-nodes/solution/huan-gen-dppythonjavacgo-by-endlesscheng-ccwy/
class Solution {private List<Integer>[] g;private Set<Long> s = new HashSet<>();private int k, ans, cnt0;public int rootCount(int[][] edges, int[][] guesses, int k) {this.k = k;g = new ArrayList[edges.length+1];Arrays.setAll(g, e -> new ArrayList<>());for(int[] e : edges){int x = e[0], y = e[1];g[x].add(y);g[y].add(x); // 建图}for(int[] e : guesses){ // guesses 转换成哈希表,加快查询速度s.add((long) e[0] << 32 | e[1]); // 两个 4 字节数压缩成一个 8 字节数Long}dfs(0, -1);reroot(0,-1,cnt0);return ans;}private void dfs(int x, int fa){for(int y : g[x]){if(y != fa){if(s.contains((long) x << 32 | y)) // 以 0 为根时,猜对了cnt0++;dfs(y,x);}}}private void reroot(int x, int fa, int cnt){if(cnt >= k) ans++;// 此时 cnt 就是以 x 为根时的猜对次数for(int y : g[x]){if(y != fa){int c = cnt;if(s.contains((long) x << 32 | y)) c--;// 原来是对的,现在错了if(s.contains((long) y << 32 | x)) c++;// 原来是对的,现在错了reroot(y,x,c);}}}
}
rivate void reroot(int x, int fa, int cnt){
if(cnt >= k) ans++;// 此时 cnt 就是以 x 为根时的猜对次数
for(int y : g[x]){
if(y != fa){
int c = cnt;
if(s.contains((long) x << 32 | y)) c–;// 原来是对的,现在错了
if(s.contains((long) y << 32 | x)) c++;// 原来是对的,现在错了
reroot(y,x,c);
}
}
}
}
相关文章:

双周赛99(贪心、数学、区间合并计算、换根DP)
文章目录双周赛99[6312. 最小和分割](https://leetcode.cn/problems/split-with-minimum-sum/)贪心[6311. 统计染色格子数](https://leetcode.cn/problems/count-total-number-of-colored-cells/)找规律[6313. 统计将重叠区间合并成组的方案数](https://leetcode.cn/problems/c…...
 客户案例——弗吉尼亚理工大学)
OpenText Exceed TurboX(ETX) 客户案例——弗吉尼亚理工大学
弗吉尼亚理工大学简化了高性能计算的使用。OpenText Exceed TurboX 提供高性能图形远程应用程序访问,提高工作效率 挑战 图形界面响应缓慢,影响用户使用; 对复制应用程序输出文件进行本地分析时,影响带宽和速度; 使用…...
【Python】torch.norm()用法解析
【Python】torch.norm()用法解析 文章目录【Python】torch.norm()用法解析1. 介绍1.1 p-范数1.2 Frobenius 范数1.3 核范数2. API3. 示例1. 介绍 torch.norm()是对输入的tensor求对应的范数。tensor的范数有以下三种: 1.1 p-范数 1.2 Frobenius 范数 即ÿ…...
)
C++核心编程<内存分区模型>(1)
C核心编程<内存分区模型>1.内存分区模型1.1内存分区模型概述1.2内存分区的意义1.3程序允许前1.3.1代码区1.3.2全局区1.3.2.1全局区的演示1.4程序运行后1.4.1栈区1.4.1.1栈区演示1.4.2堆区1.4.2.1堆区演示1.5new操作符1.5.1new操作的概述1.内存分区模型 1.1内存分区模型概…...
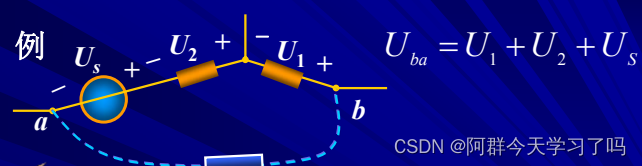
电路基础(1)电路模型和电路定律
电路中的电压、电流之间具有两种约束,一种是由电路元件决定的元件约束;另一种是元件间连接而引入的几何约束(就是拓扑约束),后者由基尔霍夫定律来表达。基尔霍夫定律是集总参数电路的基本定律。 1.电路和电路模型电源又…...

pytest 基础
pytest安装 安装 pip install -U pytest 验证安装 pytest --version 约束: 所有的测试文件名都需要满足test_ *.py格式或* _test.py格式。 测试文件中的测试类以Test_开头,并且不能带有 init 方法。 测试类中可以包含一个或多个test_开头的函数。 步骤…...
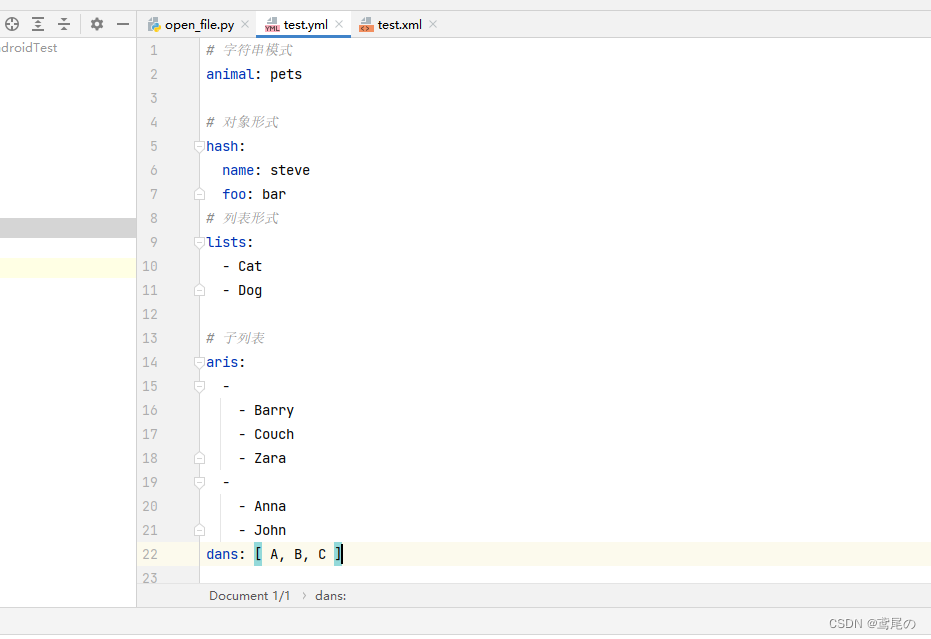
软测入门(七)python操作数据文件(Json、yaml、csv、excel、xml)
python操作文件 txt文件 read() : 读取所有readline() : 读取一行readlines() : 读取所有,且以行为单位,放入list列表中 file open(r"F:\abc.txt", "r", encoding"utf-8") # 以utf-8格式读取文件 # 读取所有 # print…...
【小程序】django学习笔记1
网页能用,不知道小程序能不能用。应该能吧。。。。。创建django程序文件包,xxx处是给该文件夹起个名django-admin startproject xxx一个project是由很多个app(小应用)组成的在文件夹目录下创建一个app,xxx处给该app起个…...
MySQL常用函数整理
MySQL常用函数整理sql函数分类一、流程控制1、判断值为null或空字符串2、IF函数3、IFNULL函数4、CASE函数(1) 相当于switch case的作用(2) 相当于if elseif的作用5、COALESCE函数二、字符串类(GBT答案)1、用于select、insert等子句中2、用于where子句中其…...

设计模式—“组件协作”
现代软件专业分工之后的第一个结果是“框架与应用程序的划分”,“组件协作”模式通过晚期绑定,来实现框架与应用程序之间的松耦合,是二者之间协作时常用的模式。 典型模式有:Template Method、Observer、Strategy 一、Template Method 动机 在软件构建过程中,对于某一…...

vue里使用driver.js实现项目功能向导指引
介绍 https://github.com/kamranahmedse/driver.js driver.js 是一个轻量级、无依赖的原生JavaScript引擎,在整个页面中驱动用户的注意力,强大的、高度可定制的原生JavaScript引擎,无外部依赖,支持所有主流浏览器。 安装 npm …...
详解JAVA类加载
目录 1.概述 2.双亲委派 3.ServiceClassLoader 4.URLClassLoader 5.加载冲突 1.概述 概念: 类加载器(Class Loader)是Java虚拟机(JVM)的一个重要组件,负责加载Java类到内存中并使其可以被JVM执行。类…...

高斯分布、高斯混合模型、EM算法详细介绍及其原理详解
相关文章 K近邻算法和KD树详细介绍及其原理详解朴素贝叶斯算法和拉普拉斯平滑详细介绍及其原理详解决策树算法和CART决策树算法详细介绍及其原理详解线性回归算法和逻辑斯谛回归算法详细介绍及其原理详解硬间隔支持向量机算法、软间隔支持向量机算法、非线性支持向量机算法详细…...
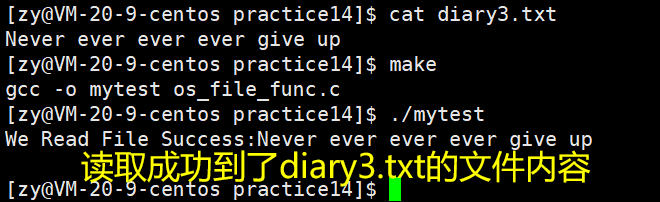
[Linux入门篇]一篇博客解决C/C++/Linux System Call文件操作接口的使用
目录 0.前言 1.C / C ->文件操作 1.1 C语言文件操作 1.1.1 C语言文件打开/关闭/写入 1.1.2 C语言文件的追加操作 1.1.3 C语言文件的读取 1.2 C语言文件操作 1.2.1 C文件打开 / 关闭 / 写入 1.2.2 C文件读取 1.2.3 文件追加 2.三个默认输入输出流 2.1 C语言中的三…...

数据结构和算法学习记录——删除有序数组中的重复项、合并两个有序数组
去重删除有序数组中的重复项题目来自:https://leetcode.cn/problems/remove-duplicates-from-sorted-array/description/题目描述给你一个 升序排列 的数组 nums ,请你原地删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数…...

FPGA实现模拟视频BT656解码 TW2867四路PAL采集拼接显示 提供工程源码和技术支持
目录1、前言2、模拟视频概述3、模拟视频颜色空间4、逐行与隔行5、BT656数据与解码BT656数据格式BT656数据解码6、TW2867芯片解读与配置TW2867芯片解读TW2867芯片配置TW2867时序分析7、设计思路与框架8、vivado工程详解9、上板调试验证10、福利:工程代码的获取1、前言…...
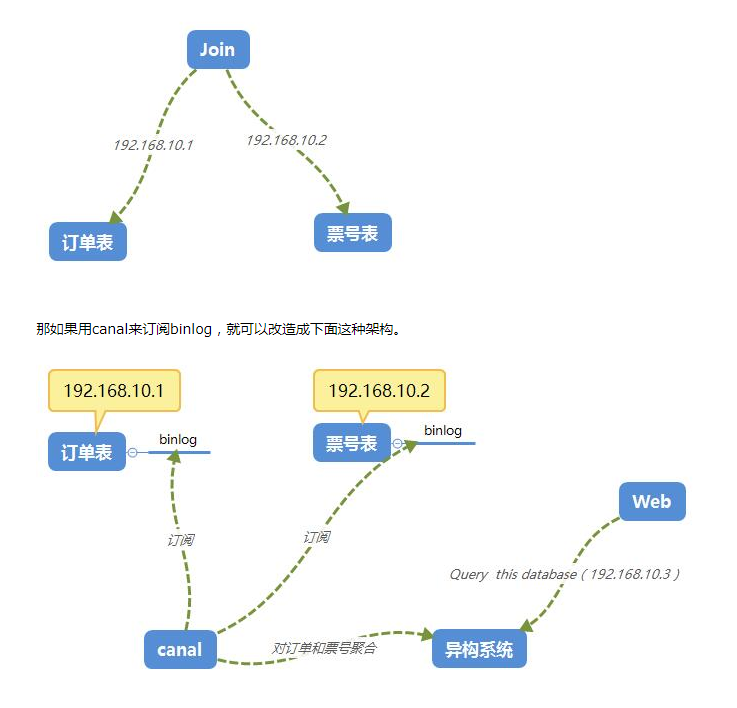
【建议收藏】超详细的Canal入门,看这篇就够了!!!
概述 canal是阿里巴巴旗下的一款开源项目,纯Java开发。基于数据库增量日志解析,提供增量数据订阅&消费,目前主要支持了MySQL(也支持mariaDB)。 背景 早期,阿里巴巴B2B公司因为存在杭州和美国双机房部…...

KubeSphere 社区双周报 | OpenFunction v1.0.0-rc.0 发布
KubeSphere 社区双周报主要整理展示新增的贡献者名单和证书、新增的讲师证书以及两周内提交过 commit 的贡献者,并对近期重要的 PR 进行解析,同时还包含了线上/线下活动和布道推广等一系列社区动态。 本次双周报涵盖时间为:2023.02.17-2023.…...

查漏补缺3月
SPI扩展序列化方式 分布式ID的相关问题 TCP的流量控制,避免浪费网络资源的滑动平均法也可以用在其他可能会出现资源浪费的情况等 讲一讲对自己这个 RPC 项目的想法,你是怎么设计这个项目的,想要实现那些功能? 你认为一个好的 RPC…...

如何使用Java实现类似Windows域登录
什么是域登录? 域登录是一种集中式身份验证和授权方法,用于访问企业内部网络和资源。在Windows环境中,域是一组计算机和用户帐户的集合,受到单个安全管理的控制。域登录允许用户在访问域资源时使用单个帐户名和密码进行身份验证&…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
