每周一算法:双向深搜
题目描述
达达帮翰翰给女生送礼物,翰翰一共准备了 N N N 个礼物,其中第 i i i 个礼物的重量是 G [ i ] G[i] G[i]。
达达的力气很大,他一次可以搬动重量之和不超过 W W W的任意多个物品。
达达希望一次搬掉尽量重的一些物品,请你告诉达达在他的力气范围内一次性能搬动的最大重量是多少。
输入格式
第一行两个整数,分别代表 W W W 和 N N N。
以后 N N N行,每行一个正整数表示 G [ i ] G[i] G[i]。
输出格式
仅一个整数,表示达达在他的力气范围内一次性能搬动的最大重量。
数据范围
1 ≤ N ≤ 46 1≤N≤46 1≤N≤46,
1 ≤ W , G [ i ] ≤ 2 31 − 1 1≤W,G[i]≤2^{31}−1 1≤W,G[i]≤231−1
输入样例
20 5
7
5
4
18
1
输出样例
19
算法思想
根据题目描述,需要从给定的 N N N个数中选择几个,使它们的和最接近 W W W,属于“子集和”问题的扩展;当然也可以从背包问题的角度去思考解决,但是这里背包的“体积”过大( 1 ≤ W ≤ 2 31 − 1 1≤W≤2^{31}−1 1≤W≤231−1),时间和空间复杂度都不允许。
这类问题的直接解法就是进行“指数型”枚举,搜索每个礼物选还是不选,时间复杂度为 O ( 2 N ) O(2^N) O(2N)。此题 N ≤ 46 N≤46 N≤46, 2 46 2^{46} 246的复杂度过高,可以利用双向深搜的思想进行优化。
双向深搜
除了迭代加深之外,双向深搜也可以避免在深层子树上浪费时间。
在一些题目中,问题不但具有“初态”,还具有明确的“终态”,并且从初态开始搜索与从终态开始逆向搜索产生的搜索树都能覆盖整个状态空间。在这种情况下,就可以采用双向搜索——从初态和状态出发各搜索一半,产生的两棵深度减半的搜索树,在中间交汇、组成最终答案。避免了层数过深时,分支数量的大规模增长。
下图是直接进行一次搜索产生的搜索树:
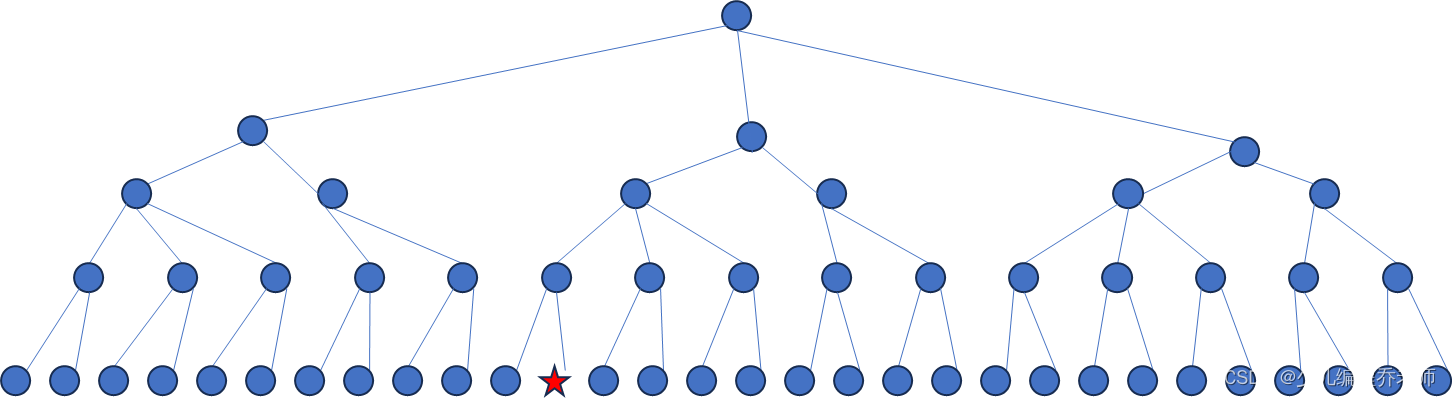
下图是双向搜索的两棵搜索树,避免了避免了层数过深时,分支数量的大规模增长。
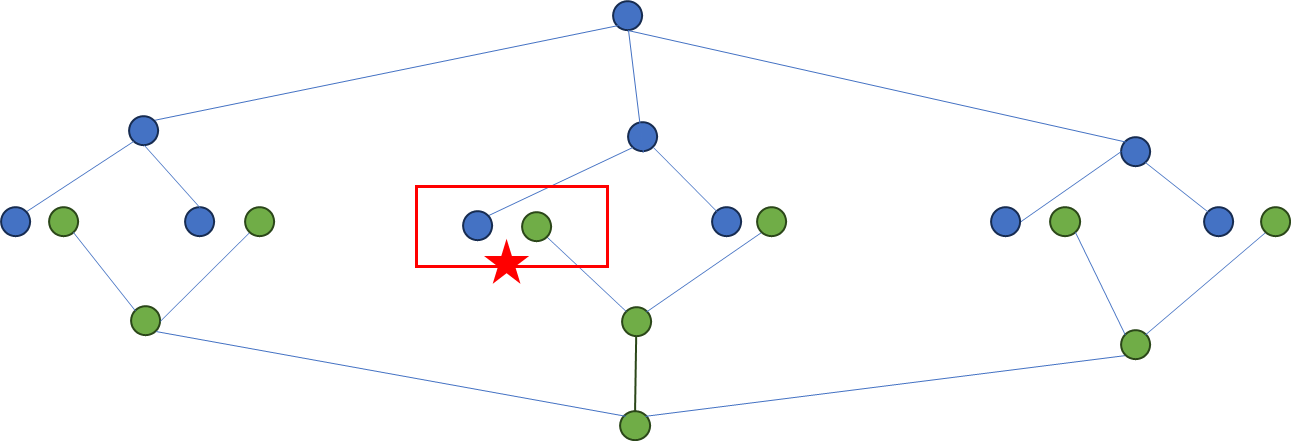
算法实现
将礼物分成两部分
- 首先,从前一半礼物中枚举出所有组合,将可能达到 0 ∼ W 0\sim W 0∼W之间的所有重量值,存放在一个数组 a [ ] a[] a[]中,并对数组进行排序、去重
- 然后,进行第二次搜索,尝试从后一半礼物中枚举出所有组合,对于每个可能达到的重量 k k k,在第一部分得到的数组 a [ ] a[] a[]中查找 k + a [ i ] ≤ W k+a[i]\le W k+a[i]≤W的最大值,可以使用二分查找。
这样,算法的时间复杂度为 O ( 2 N 2 × l o g N 2 ) O(2^{\frac{N}{2}}\times log\frac{N}{2}) O(22N×log2N)。
代码实现
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 50;
int w[N];
int cnt, a[1 << 25]; //存储前一半礼物所有组合的重量
int n, W, ans;
void dfs1(int i, int k) //k表示目前组合的重量
{if(i == n / 2) //只搜索前一半的礼品{a[cnt ++] = k; //将组合得到的重量存到a数组return;}if((LL)k + w[i] <= W) dfs1(i + 1, k + w[i]); //装得下第i件礼物dfs1(i + 1, k); //不装第i件礼物
}
void dfs2(int i, int k)
{if(i == n) //搜索完成,二分查找不超过W的最大组合重量{int L = 0, R = cnt - 1;while(L < R){int mid = (L + R + 1) / 2;if((LL)k + a[mid] <= W) L = mid;else R = mid - 1;}ans = max(ans, k + a[L]);return;}if((LL)k + w[i] <= W) dfs2(i + 1, k + w[i]); //装得下第i件礼物dfs2(i + 1, k); //不装第i件礼物
}
int main()
{cin >> W >> n;for(int i = 0; i < n; i ++) cin >> w[i];//优化搜索顺序,优先搜索重量较大的礼品sort(w, w + n);reverse(w, w + n);dfs1(0, 0); //枚举前一半礼品的组合,将其组合得到的重量存到a数组sort(a, a + cnt); //对前一半礼物组合得到的重量排序去重cnt = unique(a, a + cnt) - a;//对后一半礼物进行搜索dfs2(n / 2, 0);cout << ans;return 0;
}
相关文章:

每周一算法:双向深搜
题目描述 达达帮翰翰给女生送礼物,翰翰一共准备了 N N N 个礼物,其中第 i i i 个礼物的重量是 G [ i ] G[i] G[i]。 达达的力气很大,他一次可以搬动重量之和不超过 W W W的任意多个物品。 达达希望一次搬掉尽量重的一些物品,请…...

蓝桥杯刷题(十)
1.翻转 代码 输入数据,每组数据进行比较,j的范围掐头去尾,若a[j]b[j],继续,若出现010,101子串则改成000,111,遍历完后比较a是否等于b,相同则输出次数,不同则输出-1。 for _ in ran…...
ioDraw:与 GitHub、gitee、gitlab、OneDrive 无缝对接,绘图文件永不丢失!
🌟 绘图神器 ioDraw 重磅更新,文件保存再无忧!🎉 无需注册,即刻畅绘!✨ ioDraw 让你告别繁琐注册,尽情挥洒灵感! 新增文件在线实时保存功能,支持将绘图文件保存到 GitHu…...

利用 Python 处理遥感影像数据:计算年度平均影像
在地球科学、气象学以及环境监测等领域,遥感影像数据是一种重要的信息源,它们可以提供地表的地形、植被覆盖、气候变化等丰富信息。然而,随着观测技术的进步,我们通常会获得大量的遥感影像数据,如何高效地处理和分析这…...
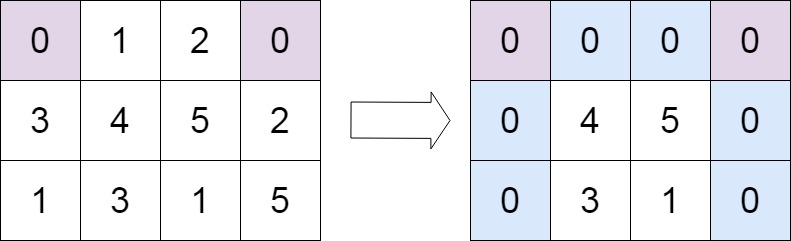
【Leetcode-73.矩阵置零】
题目: 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 示例 1: 输入:matrix [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]示例 2&…...

redis 常见的异常
目录 一、缓存穿透 1、概念 解决方案 (1)布隆过滤器 (2)、缓存空对象 二、缓存雪崩 1、概念 解决方案 (1)redis高可用 (2)限流降级 (3)数据预热 一、缓存穿透 1、概念 缓…...
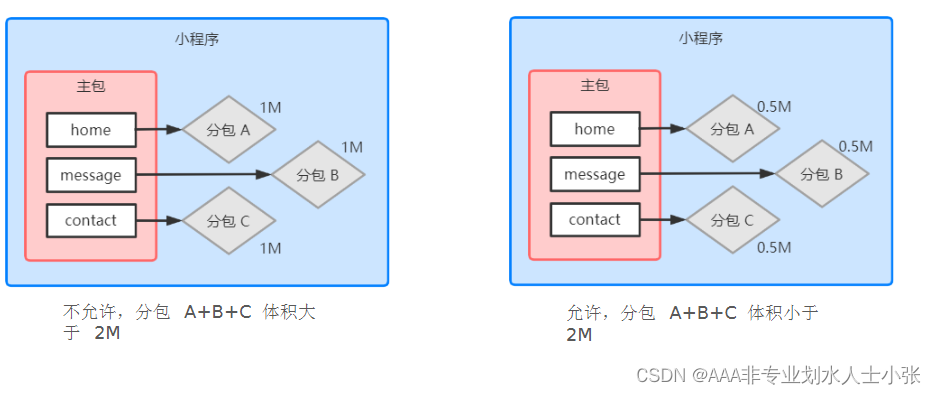
npm包、全局数据共享、分包
使用 npm 包 小程序对 npm 的支持与限制 目前,小程序中已经支持使用 npm 安装第三方包,从而来提高小程序的开发效率。但是,在小程序中使用npm 包有如下 3 个限制: ① 不支持依赖于 Node.js 内置库的包 ② 不支持依赖于浏览器内置…...

UnityShader:IBL
效果: 实现: Shader "MyShader/IBL" {Properties{_CubeMap ("环境贴图", Cube) "white" {}_Exposure("曝光",float)1.0_Color("颜色",color)(1,1,1,1)_NormalMap("法线贴图",2d)"bu…...

每日五道java面试题之mybatis篇(三)
目录: 第一题. MyBatis的框架架构设计是怎么样的?第二题. 为什么需要预编译?第三题. Mybatis都有哪些Executor执行器?它们之间的区别是什么?第四题. Mybatis中如何指定使用哪一种Executor执行器?第五题. Mybatis是否支持延迟加载…...

C#开发五子棋游戏:从新手到高手的编程之旅
C#开发五子棋游戏:从新手到高手的编程之旅 目录 一、引言 二、项目规划与设计思路 三、棋盘与棋子的数据模型构建 四、交互式用户界面设计 五、核心游戏逻辑实现 一、引言 五子棋,作为一种古老的策略型棋类游戏,在全球拥有广泛的爱好者…...
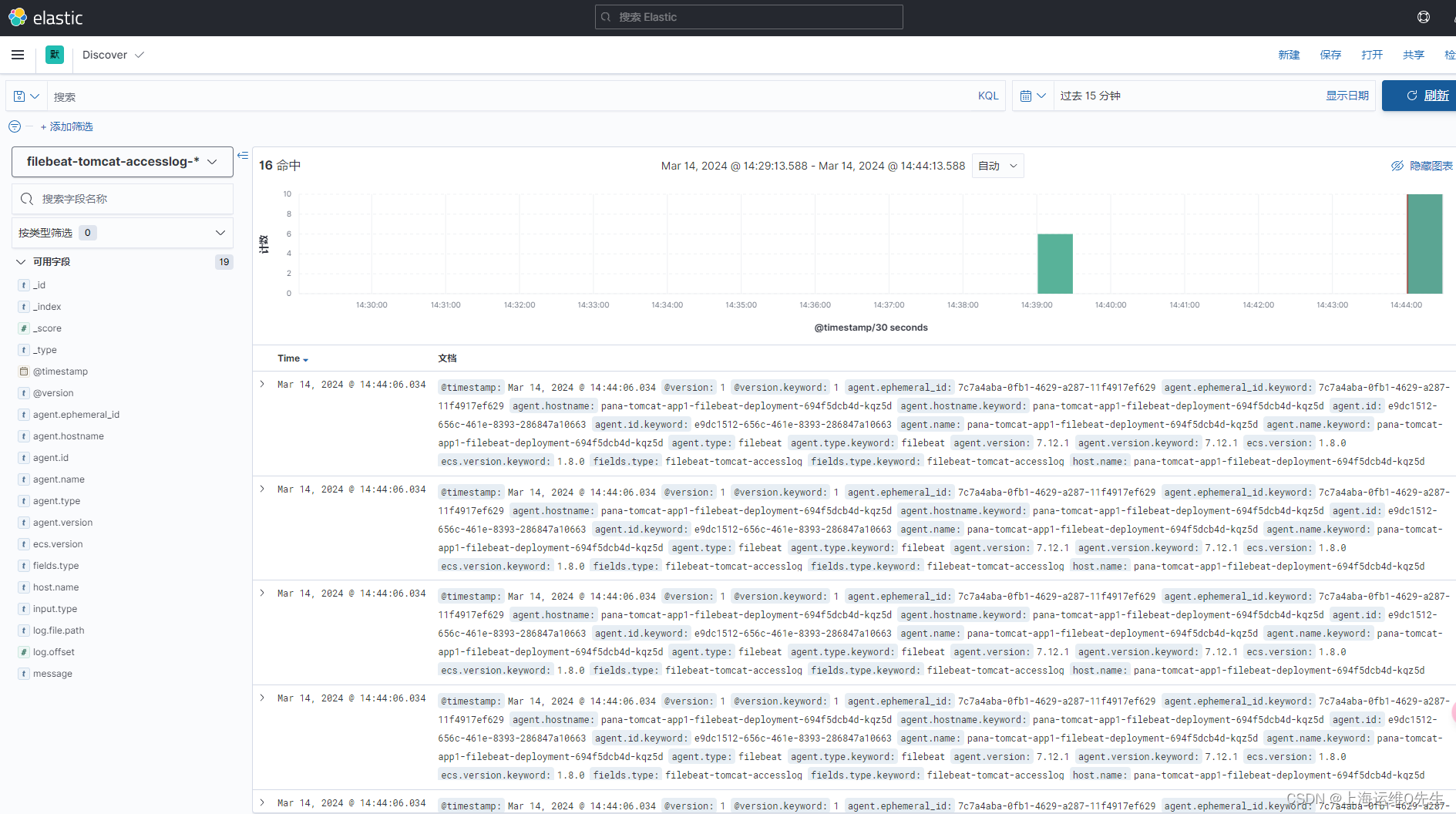
ELK日志管理实现的3种常见方法
ELK日志管理实现的3种常见方法 1. 日志收集方法 1.1 使用DaemonSet方式日志收集 通过将node节点的/var/log/pods目录挂载给以DaemonSet方式部署的logstash来读取容器日志,并将日志吐给kafka并分布写入Zookeeper数据库.再使用logstash将Zookeeper中的数据写入ES,并通过kibana…...

深度强化学习01
Random variable Probability Density Function 期望 Random Sampling 学习视频 这绝对是我看过最好的深度强化学习!从入门到实战,7小时内干货不断!_哔哩哔哩_bilibili...
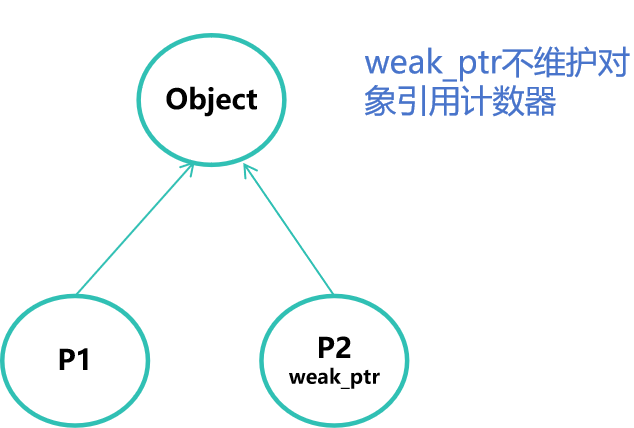
C++ 智能指针的使用
智能指针类型 在C程序中,普通变量使用栈内存,为函数运行时专用,结束后会自动释放,无须考虑内存释放问题。 但堆内存是共用的,其使用是通过指针变量的new来分配,使用delete来释放,因指针使用方便…...
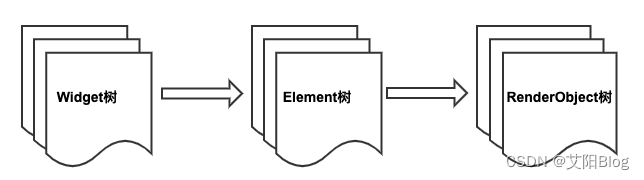
Flutter 核心原理 - UI 框架(UI Framework)
Flutter 既能保证很高的开发效率,又能获得很好的性能。 这两年 Flutter 技术热度持续提高,整个 Flutter 生态和社区也发生了翻天覆地的变化。目前Flutter 稳定版发布到了3.0,现在已经支持移动端、Web端和PC端,通过Flutter 开发的…...

Hive优化
工作中涉及到优化部分不多,下面的一些方案可能会缺少实际项目支撑,这里主要是为了完备一下知识体系。 参考的hive参数管理文档地址:https://cwiki.apache.org/confluence/display/Hive/ConfigurationProperties 对于Hive优化,可以…...

React 的 diff 算法
React 的 diff 算法的演进。 在 React 16 之前,React 使用的是称为 Reconciliation 的 diff 算法。Reconciliation 算法通过递归地比较新旧虚拟 DOM 树的每个节点,找出节点的差异,并将这些差异应用到实际的 DOM 上。整个过程是递归的&#x…...
综合知识篇07-软件架构设计考点(2024年软考高级系统架构设计师冲刺知识点总结系列文章)
专栏系列文章: 2024高级系统架构设计师备考资料(高频考点&真题&经验)https://blog.csdn.net/seeker1994/category_12593400.html案例分析篇00-【历年案例分析真题考点汇总】与【专栏文章案例分析高频考点目录】(2024年软考高级系统架构设计师冲刺知识点总结-案例…...
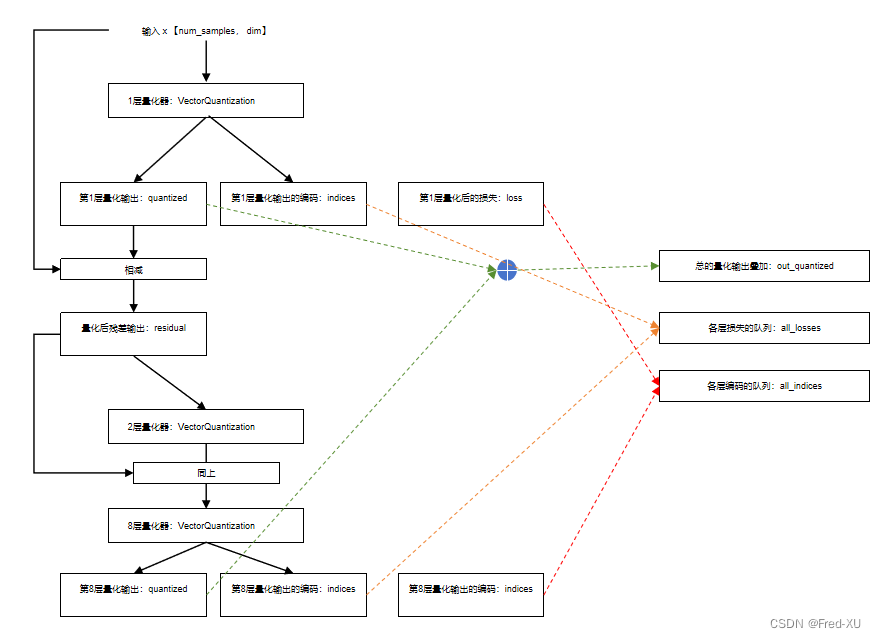
【GPT-SOVITS-05】SOVITS 模块-残差量化解析
说明:该系列文章从本人知乎账号迁入,主要原因是知乎图片附件过于模糊。 知乎专栏地址: 语音生成专栏 系列文章地址: 【GPT-SOVITS-01】源码梳理 【GPT-SOVITS-02】GPT模块解析 【GPT-SOVITS-03】SOVITS 模块-生成模型解析 【G…...

Flutter第四弹:Flutter图形渲染性能
目标: 1)Flutter图形渲染性能能够媲美原生? 2)Flutter性能优于React Native? 一、Flutter图形渲染原理 1.1 Flutter图形渲染原理 Flutter直接调用Skia。 Flutter不使用WebView,也不使用操作系统的原生控件,而是…...
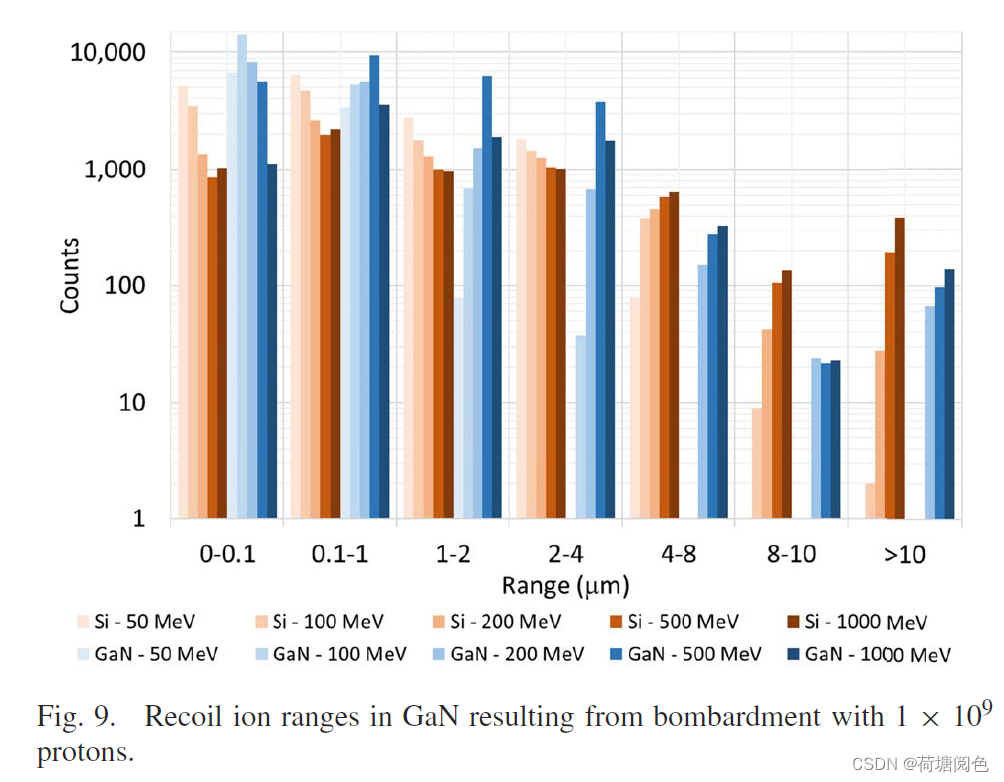
[氮化镓]GaN中质子反冲离子的LET和射程特性
这篇文件是一篇关于氮化镓(GaN)中质子反冲离子的线性能量转移(LET)和射程特性的研究论文,发表在《IEEE Transactions on Nuclear Science》2021年5月的期刊上。论文的主要内容包括: 研究背景:氮…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
