654. 最大二叉树
题目
leetcode题目地址
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
创建一个根节点,其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
示列1
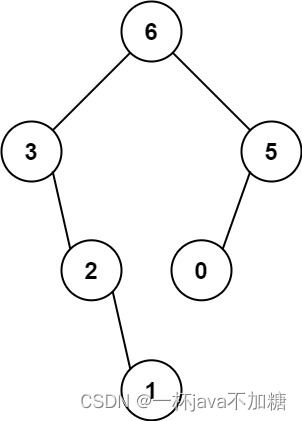
输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。- 空数组,无子节点。- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。- 空数组,无子节点。- 只有一个元素,所以子节点是一个值为 1 的节点。- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。- 只有一个元素,所以子节点是一个值为 0 的节点。- 空数组,无子节点。示列2
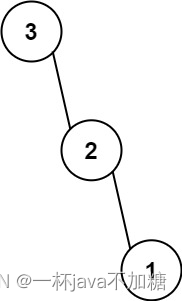
输入:nums = [3,2,1]
输出:[3,null,2,null,1]
提示:
- 1 <= nums.length <= 1000
- 0 <= nums[i] <= 1000
- nums 中的所有整数 互不相同
code
递归:
- 确定函数的参数和返回值。参数是数组,返回值是节点。
- 确定递归终止条件。当没有元素时,返回null;当只有一个元素时,证明是叶子节点了,返回该节点。
- 找出每一次递归的逻辑。
找出最大值的下标,将最大值作为根节点,根据最大值下标划分区别。最大值下标左边,构造左子树;最大值下标右边,构造右子树。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {return constructMaximumBinaryTreeRec(nums,0,nums.length);}public TreeNode constructMaximumBinaryTreeRec(int[] nums,int leftIndex,int rightIndex){// 没有元素了if(rightIndex - leftIndex <1){return null;}// 只有一个元素了if(rightIndex-leftIndex == 1){return new TreeNode(nums[leftIndex]);}int maxIndex = leftIndex; // 最大值的索引位置int maxVal = nums[maxIndex]; // 最大值for(int i=leftIndex+1;i<rightIndex;i++){if(nums[i]>maxVal){maxVal = nums[i];maxIndex = i;}}// 划分左右子树TreeNode node = new TreeNode(maxVal);node.left = constructMaximumBinaryTreeRec(nums,leftIndex,maxIndex);node.right = constructMaximumBinaryTreeRec(nums,maxIndex+1,rightIndex);return node;}
}
相关文章:

654. 最大二叉树
题目 leetcode题目地址 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建: 创建一个根节点,其值为 nums 中的最大值。 递归地在最大值 左边 的 子数组前缀上 构建左子树。 递归地在最大值 右边 的 子数组后缀上 构建右子树。 返…...
快速幂----快速求解底数的n次幂
目录 一.快速幂 1.问题的引入 2.快速幂的介绍 3.核心思想 4.代码实现 2.猴子碰撞的方法数 1.题目描述 2.问题分析 3.代码实现 一.快速幂 1.问题的引入 问题:求解num的n次幂,结果需要求余7 对于这个问题我们可能就是直接调用函数pow(a,b)来直接求解a的b次幂问题,但是如果…...
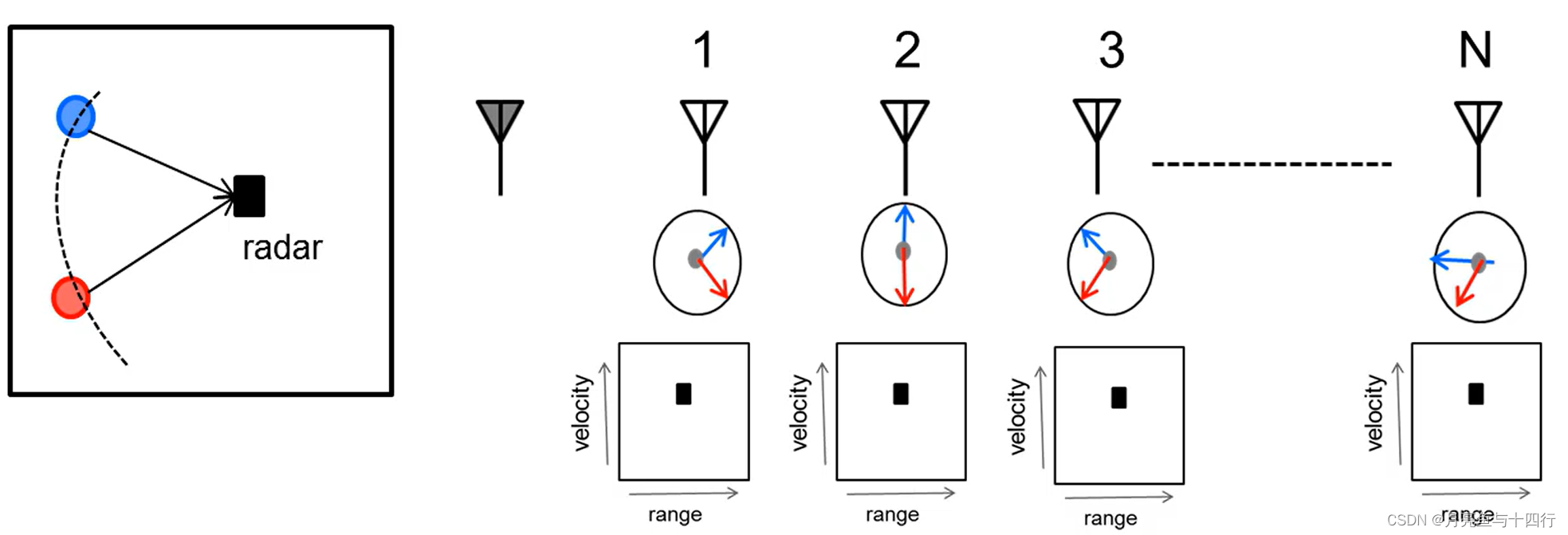
【FMCW 04】测角-Angle FFT
在之前的文章中,我们已经详尽讨论过FMCW雷达测距和测速的原理,现在来讲最后一块内容,测角。测角对于硬件设备具有要求,即要求雷达具有多发多收结构,从而形成多个空间信道(channel),我…...

Linux操作系统学习(线程同步)
文章目录线程同步条件变量生产者与消费者模型信号量环形队列应用生产者消费者模型线程同步 现实生活中我们经常会遇到同一个资源多个人都想使用的问题,例如游乐园过山车排队,玩完的游客还想再玩,最好的办法就是玩完的游客想再玩就去重新排…...

了解动态规划算法:原理、实现和优化指南
动态规划 详细介绍例子斐波那契数列最长回文子串优化指南优化思路斐波那契数列优化最长回文子串优化详细介绍 动态规划(Dynamic Programming,简称 DP)是一种通过将原问题拆分成子问题并分别求解这些子问题来解决复杂问题的算法思想。 它通常用于求解优化问题,它的核心思想…...

《NFL橄榄球》:明尼苏达维京人·橄榄1号位
明尼苏达维京人(英语:Minnesota Vikings)是一支职业美式足球球队,位于明尼苏达州的明尼阿波利斯。他们现时在国家橄榄球联合会北区参与国家美式足球联盟比赛。该球队本为美国美式足球联盟(AFL)的球队。但是…...
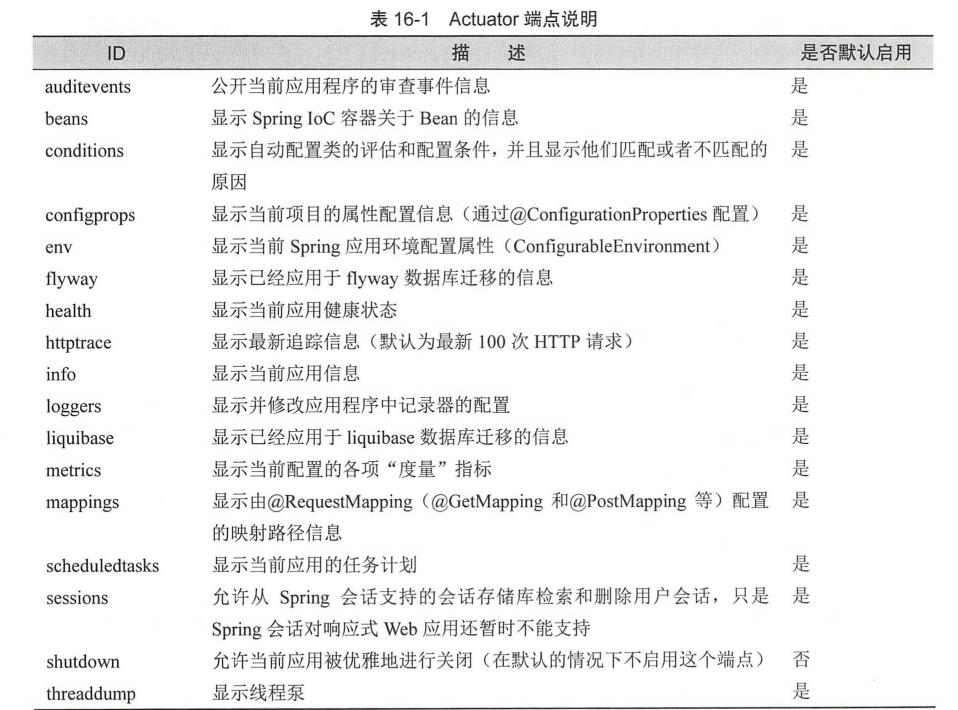
sheng的学习笔记-Actuator健康监控
前言在微服务系统里,对微服务程序的运行状况的跟踪和监控是必不可少的;例如GPE,TelegrafinfluxDB都提供了微服务体系监控的方案, ZIPKIN, Skywalking都提供了微服务云体系的APM的方案; 这些解决方案功能全面…...

初次使用ESP32-CAM记录
模块的配置和图片 摄像头:8225N V2.0 171026 模块esp-32s 参考资料:https://docs.ai-thinker.com/esp32 配置环境 参考:https://blog.csdn.net/weixin_43794311/article/details/128622558 简单使用需要注意的地方 基本的环境配置和串口…...
)
华为OD机试真题Python实现【最长连续交替方波信号】真题+解题思路+代码(20222023)
最长连续交替方波信号 题目 输入一串方波信号,求取最长的完全连续交替方波信号,并将其输出, 如果有相同长度的交替方波信号,输出任一即可,方波信号高位用1标识,低位用0标识 如图: 说明: 一个完整的信号一定以0开始然后以0结尾, 即 010 是一个完整的信号,但101,101…...
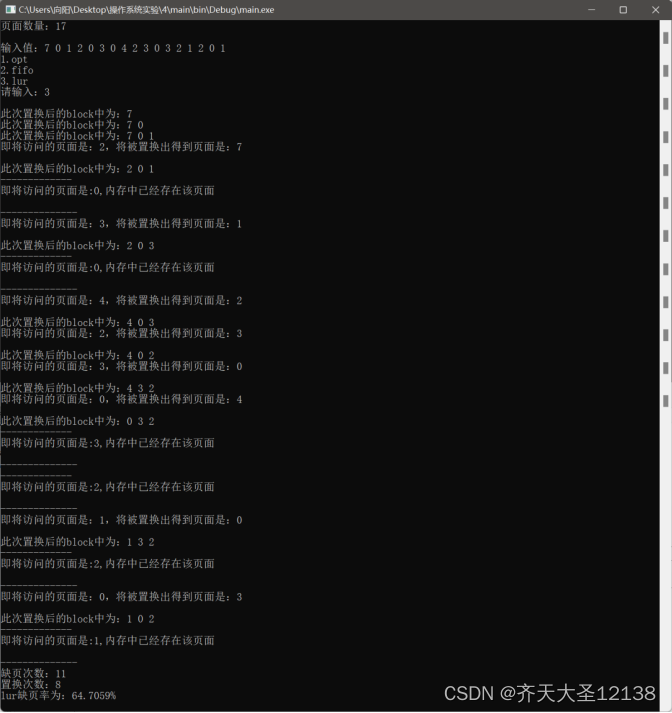
【操作系统原理实验】页面替换策略模拟实现
选择一种高级语言如C/C等,编写一个页面替换算法的模拟实现程序。1) 设计内存管理相关数据结构;2) 随机生成一个页面请求序列;3) 设置内存管理模拟的关键参数;4) 实现该页面置换算法;5) 模拟实现给定配置请求序列的换页…...

Java中解析XML文件
1 在Java中解析XML文件共有四种方式 A、DOM方式解析XML数据 树结构,有助于更好地理解、掌握,代码易于编写,在解析过程中树结构是保存在内存中,方便修改 B、SAX方式解析 采用事件驱动模式,对内存消耗比较小࿰…...
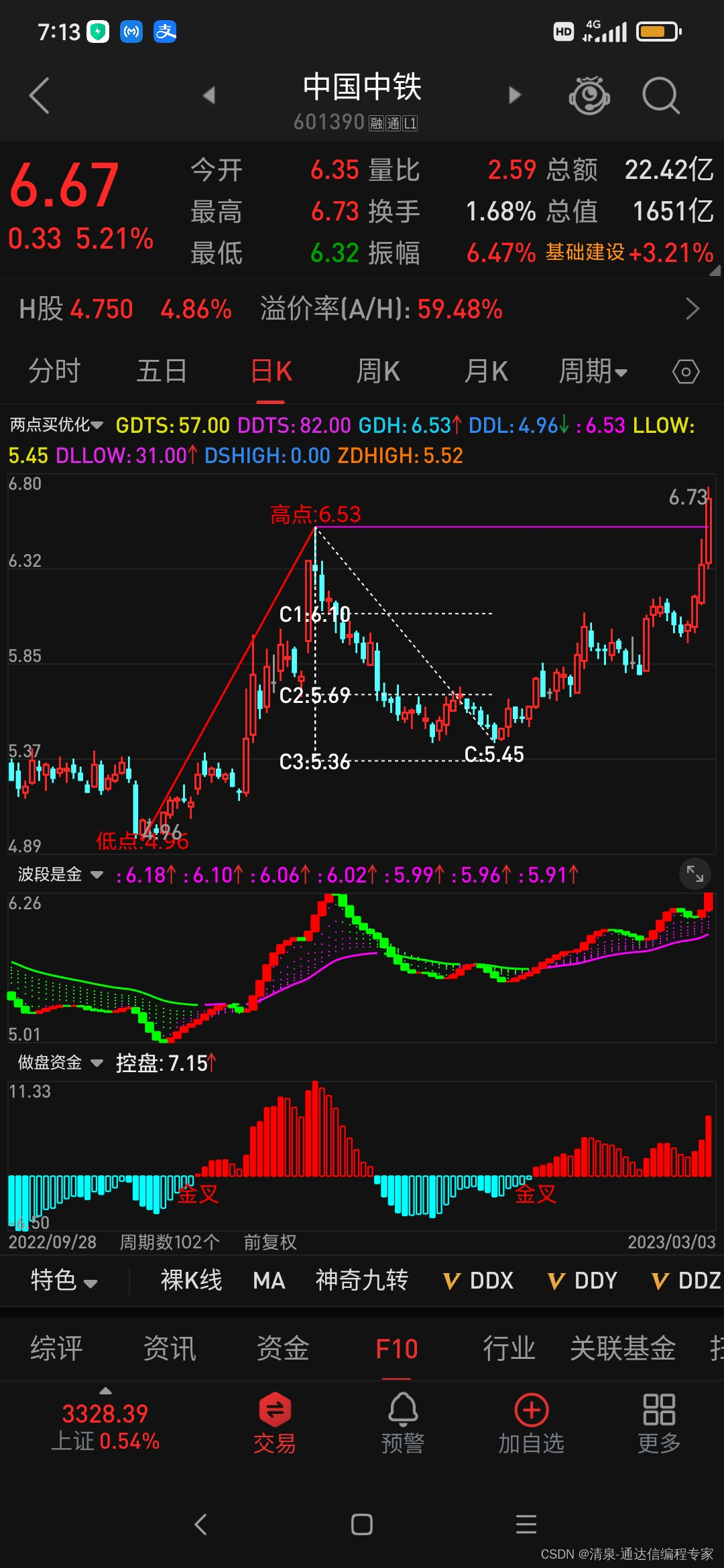
二点回调测买 源码
如图所示,两点回调测买点的效果图,这是我们常见的一种预测买点计算方法。 现将源码公布如下: DRAWKLINE(H,O,L,C); N:13; A1:REF(HIGH,N)HHV(HIGH,2*N1); B1:FILTER(A1,N); C1:BACKSET(B1,N1); D1:FILTER(C1,N); A2:REF(LOW,N)LLV(LOW,2*N1…...
钉钉端H5开发调试怎么搞
H5开发本地调试教程 作为一名前端开发,大家平时工作中或多或少都有接触或需要开发H5页面的场景,在开发过程中,如何像PC端页面一样有有丝滑的体验呢? 不同的情况需要在不同的端调试更方便有效: 1. 在画UI的时候,更适合在PC端调试,更改代码或者直接在浏览器调试,都是实…...
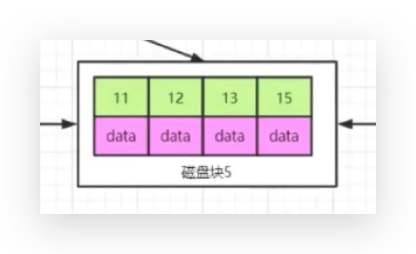
Mysql Server原理简介
Mysql客户端包括JDBC、 Navicat、sqlyog,只是为了和mysql server建立连接,向mysql server提交sql语句。mysql server组件第一部分叫连接器主要承担的功能叫管理连接和验证权限,每次在进行数据库访问的时候,必然要输入用户名和密码…...

23种设计模式-外观模式
外观模式是一种结构型设计模式,它提供了一个统一的接口,用来访问子系统中的一群接口。外观模式定义了一个高层接口,使得客户端可以更加方便地访问子系统的功能。在这篇博客中,我们将讨论如何使用Java实现外观模式,并通…...

使用 Vulkan VkImage 作为 CUDA cuArray
使用 Vulkan VkImage 作为 CUDA cuArray【问题标题】:Use Vulkan VkImage as a CUDA cuArray使用 Vulkan VkImage 作为 CUDA cuArray【发布时间】:2019-08-20 20:01:10【问题描述】:将 Vulkan VkImage 用作 CUDA cuArray 的正确方法是什么&am…...

电商API接口-电商OMS不可或缺的一块 调用代码展示
电商后台管理系统关键的一环就是实现电商平台数据的抓取,以及上下架商品、订单修改等功能的调用。这里就需要调用电商API接口。接入电商API接口后再根据自我的需求进行功能再开发,实现业务上的数字化管理。其中订单管理模板上需要用到如下API:seller_ord…...

Solaris ZFS文件系统rpool扩容
ZFS文件系统简介 Solaris10默认的文件系统是ufs(Unix Filesystem),当然也可以选装zfs;Solaris11默认的文件系统是zfs(Zettabyte Filesystem)。 ZFS文件系统的英文名称为Zettabyte File System,也叫动态文件…...
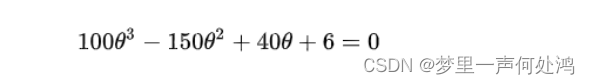
模式识别 —— 第二章 参数估计
模式识别 —— 第二章 参数估计 文章目录模式识别 —— 第二章 参数估计最大似然估计(MLE)最大后验概率估计(MAP)贝叶斯估计最大似然估计(MLE) 在语言上: 似然(likelihood…...
)
判断4位回文数-课后程序(Python程序开发案例教程-黑马程序员编著-第3章-课后作业)
实例1:判断4位回文数 所谓回文数,就是各位数字从高位到低位正序排列和从低位到高位逆序排列都是同一数值的数,例如,数字1221按正序和逆序排列都为1221,因此1221就是一个回文数;而1234的各位按倒序排列是43…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...
