L - Let‘s Swap(哈希 + 规律)
2023河南省赛组队训练赛(四) - Virtual Judge (vjudge.net)

约瑟夫最近开发了一款名为Pandote的编辑软件,现在他正在测试,以确保它能正常工作,否则,他可能会被解雇!Joseph通过实现对Pandote上字符串的复制和粘贴以及反向操作开始了他的测试。更具体地说,在每一步中,如果屏幕上的字符串是S,他将按顺序进行以下操作。1. 选择长度为l(1≤l≤IS)的前缀,则S可表示为AB (IA] = 1),注意字符串B可以为空。2. 交换这两个部分,得到字符串BA。3.反转整个字符串,得到字符串(BA)"但是,由于Pandote的功能有限,他在每一步中只能选择长度不同的前缀l1和l2。现在Joseph想知道他是否可以通过几个(可能是零)步骤将字符串S转换为T。输入输入的第一行给出了测试用例的数量T (1 <T <5 × 105)。接下来是T测试用例。对于每个测试用例,第一行包含字符串S,第二行包含字符串T。S和T都由小写拉丁字母和[S] = ITI组成。第三行包含两个整数l1和l2(1≤l1, l2≤IS1, l1 # 12),表示每一步可以选择的前缀长度。保证所有测试用例的|S]之和不超过5 × 105。
Sample 1
| Inputcopy | Outputcopy |
|---|---|
3 ljhelloh hellohlj 2 4 thisisastr htrtsasisi 3 5 abcde bcdea 1 4 | yes no yes |

题解:
我们通过枚举样例可以发现如果连续两个l1或l2操作,原字符串是不变的
(假设l1 > l2)
并且如果进行(l1,l2)
相当于把字符串向左(先l1后 l2) l1 - l2个单位
或向右移动(先l2 后l1) l1 - l2个单位
那么最终答案只可能会是
(l1,l2),l1,l2... 只在原字符串上进行向左或向右移动
l1,(l1,l2),(l1,l2)... 先进行一次l1,再同上
l2,(l1,l2),(l1,l2)... 先进行一次l2,在同上
由于我们要找循环节,所以字符串都变成二倍长度
然后哈希三种情况,看字符串T是否在三种情况中出现过
#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
#include<vector>
#include<map>
#include<queue>
#include<set>
using namespace std;
#define int long long
const int N = 4e6 + 10;
typedef pair<int, int> PII;
string s,s1,s2,c;
int n,m,a,b;
int h1[N],h2[N],h[N],p[N];
int x = 133331;
int mod = 1e9 + 7;
int res;
int get(int h[],int l,int r)
{return (h[r] - h[l-1]*p[r-l+1]%mod + mod)%mod;
}
int check(int l,int r)
{if(get(h,l,r) == res)return 1;if(get(h1,l,r) == res)return 1;if(get(h2,l,r) == res)return 1;return 0;}
void solve()
{cin >> s >> c >> a >> b;n = s.size();s1 = s.substr(a) + s.substr(0,a);reverse(s1.begin(),s1.end());s2 = s.substr(b) + s.substr(0,b);reverse(s2.begin(),s2.end());s = s + s;s = " " + s;s1 = s1 + s1;s1 = " " + s1;s2 = s2 + s2;s2 = " " + s2;c = " " + c;res = 0;p[0] = 1;for(int i = 1;i <= 2*n;i++){p[i] = (p[i-1]*x%mod);h[i] = (h[i-1]*x%mod + s[i])%mod;h1[i] = (h1[i-1]*x%mod + s1[i])%mod;h2[i] = (h2[i-1]*x%mod + s2[i])%mod;if(i <= n)res = (res*x%mod + c[i])%mod;}if(a < b)swap(a,b);for(int i = 1,j = 1;j <= n;j++){if(check(i,i+n - 1)){cout <<"yes\n";return ;}i = i + n - a + b;if(i >= n + 1){i = i%(n);if(!i)i = n;}}for(int i = 1,j = 1;j <= n;j++){if(check(i,i+n - 1)){cout <<"yes\n";return ;}i = i + a - b;if(i >= n + 1){i = i%(n);if(!i)i = n;}}cout <<"no\n";
}signed main()
{
// ios::sync_with_stdio(0);
// cin.tie(0);cout.tie(0);int t = 1;cin >> t;
//scanf("%lld",&t);while (t--) {solve();}
}
//3 F
//5 B
//6 F
//9 F
//10 B
//12 F
//15 FB
//18 FB相关文章:

L - Let‘s Swap(哈希 + 规律)
2023河南省赛组队训练赛(四) - Virtual Judge (vjudge.net) 约瑟夫最近开发了一款名为Pandote的编辑软件,现在他正在测试,以确保它能正常工作,否则,他可能会被解雇!Joseph通过实现对Pandote上字符串的复制和…...
)
c语言自动内存回收(RAII实现)
简述 什么是RAII RAII(Resource Acquisition Is Initialization)是c之父Bjarne Stroustrup提出的概念。资源一般分三个步骤:获取、使用和销毁,而在自由使用内存的c语言中,资源的销毁常常是程序员容易遗漏的事情&…...
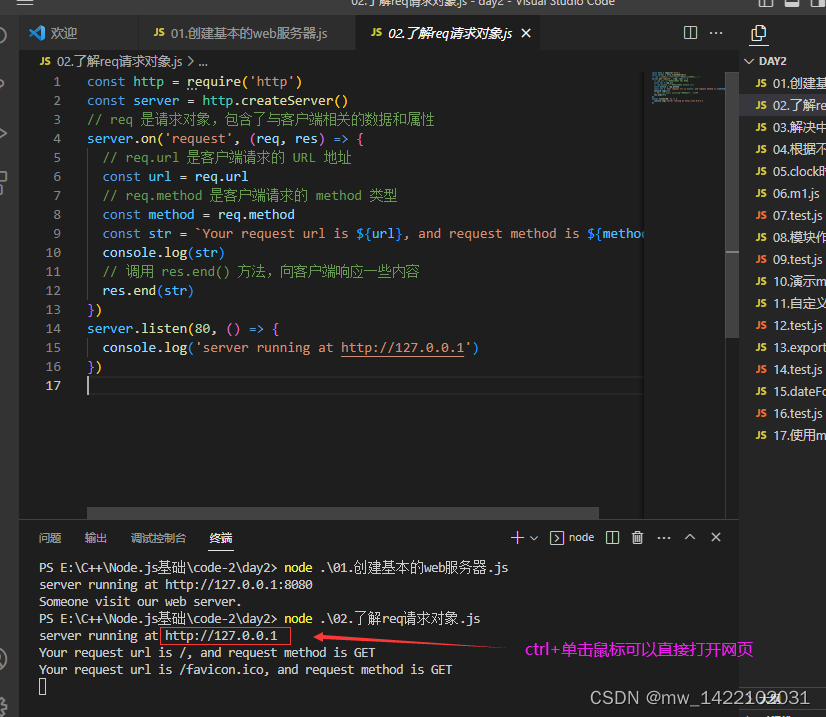
Node.js的简单学习一-----未完待续
文章目录前言学习目标一、初识Node.js1.1 回顾与思考1.1.1 需要掌握那些技术1.1.2 浏览器中的JavaScript的组成部分1.2 Node.js简介1 什么是Node.js2 Node.js中的JavaScript运行环境3 Node.js 可以做什么1.3 Node.js环境的安装1.4 在Node.js环境中执行JavaScript 代码终端中的快…...
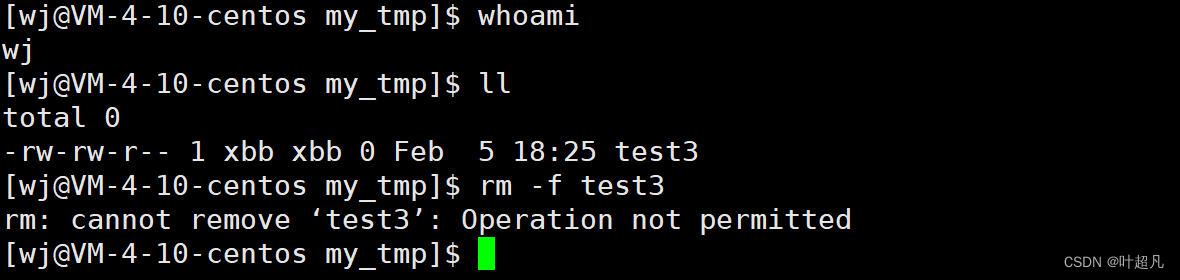
linux入门---粘滞位
为什么会有粘滞位 一台服务器有很多人使用,每个人在机器上都会有一个家目录,在家目录里可以实现自己想要的操作,但是有时候我们需要一个公共路径来完成一些操作,比如说资料分享产生临时文件的增删查改等等,这就好比我…...

关于正则表达式的讲解
以下内容源于《linux命令行与shell脚本编程大全【第三版】》一书的整理。 在shell脚本中成功运用sed编辑器和gawk程序的关键,在于熟练地使用正则表达式。 一、正则表达式的简介 1、正则表达式的定义 正则表达式(regular expression)是一个…...

贝塞尔曲线与B样条曲线
文章目录0.参考1.问题起源与插值法的曲线拟合1.1.问题起源1.2.拉格朗日插值1.3.“基”的概念1.4.插值存在的Runge现象2.贝塞尔曲线2.1.控制点的思想2.2.由控制点生成贝塞尔曲线2.3.多个控制点时的贝塞尔曲线公式2.4.贝塞尔曲线的递推公式2.5.贝塞尔曲线的性质3.B样条曲线3.1.B样…...

C语言-基础了解-24-C头文件
C头文件 一、C 头文件 头文件是扩展名为 .h 的文件,包含了 C 函数声明和宏定义,被多个源文件中引用共享。有两种类型的头文件:程序员编写的头文件和编译器自带的头文件。 在程序中要使用头文件,需要使用 C 预处理指令 #include…...
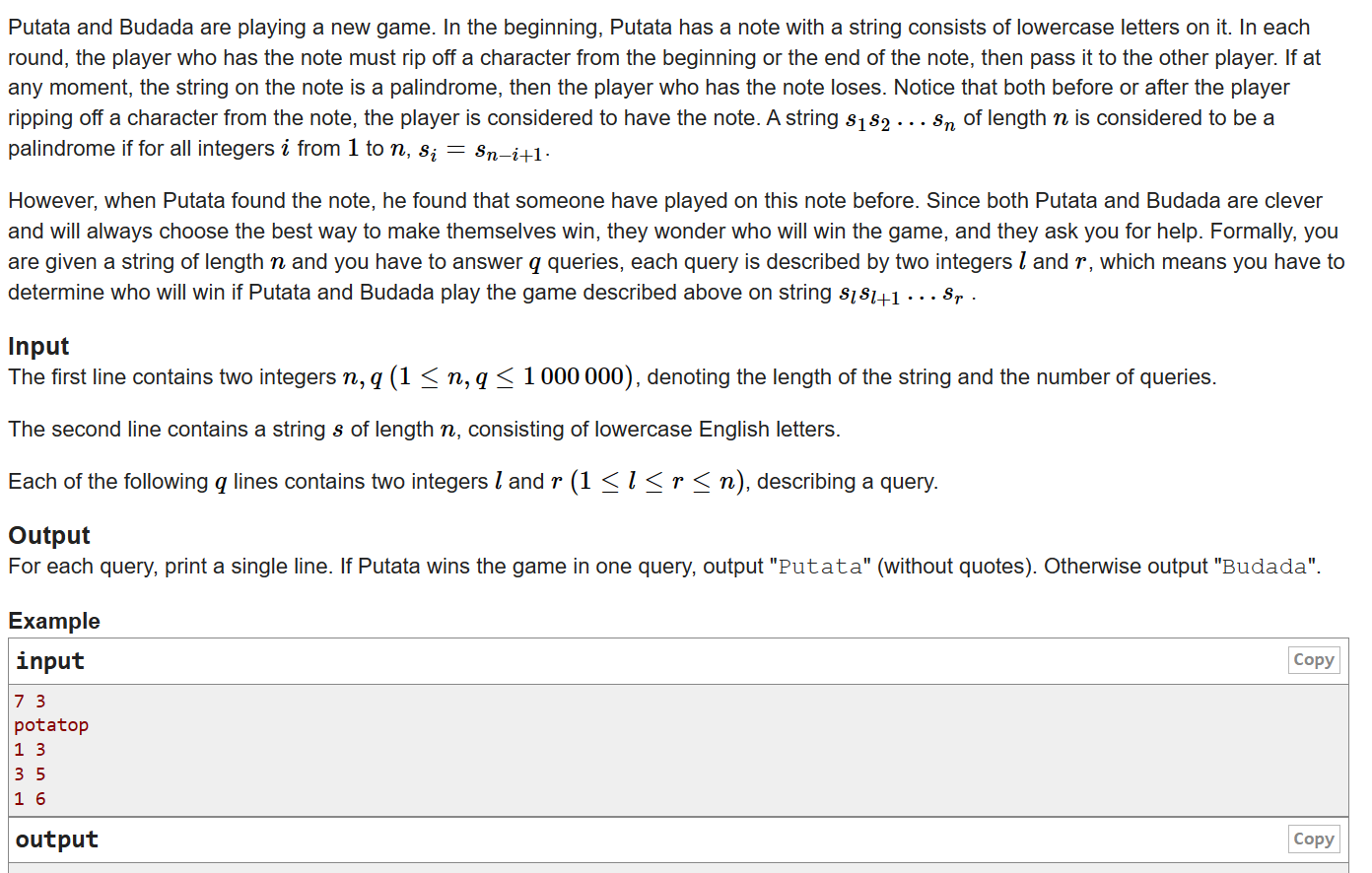
The 19th Zhejiang Provincial Collegiate Programming Contest vp
和队友冲了这场,极限6题,重罚时铁首怎么说,前面的A题我贡献了太多的罚时,然后我的G题最短路调了一万年,因为太久没写了,甚至把队列打成了优先队列,没把head数组清空完全,都是我的锅呜…...

用于<分类>的卷积神经网络、样本不平衡问题的解决
输入图像——卷积层——池化层——全连接层——输出 卷积层:核心,用来提取特征。 池化层:对特征降维。实际的主要作用是下采样,减少参数量来提高计算速度。 卷积神经网络的训练:前向传播(分类识别…...
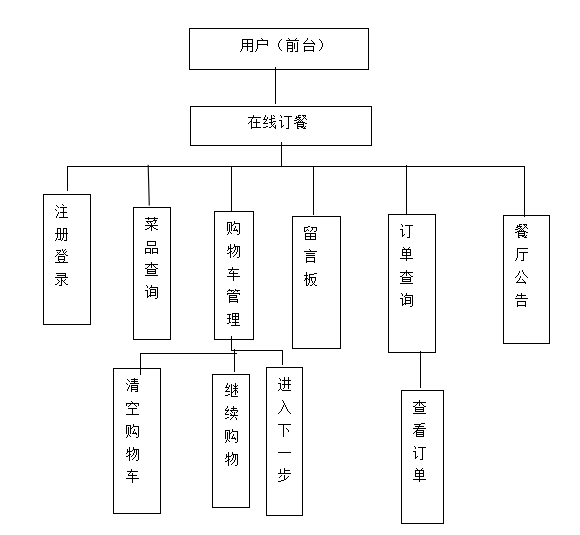
网上订餐管理系统的设计与实现
技术:Java、JSP等摘要:随着信息技术的广泛使用,电子商务对于提高管理和服务水平发挥着关键的作用。越来越多的商家开始着手于电子商务建设。电子商务的发展为人们的生活提供了极大的便利,也成为现实社会到网络社会的真实体现。当今…...

Httpclient测试
在IDEA中有一个非常方便的http接口测试工具httpclient,下边介绍它的使用方法,后边我们会用它进行接口测试。如果IDEA版本较低没有自带httpclient,需要安装httpclient插件1.插件2.controller进入controller类,找到http接口对应的方…...
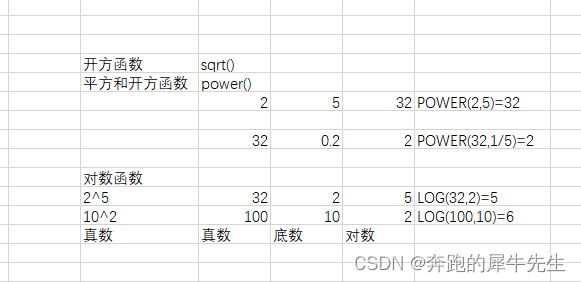
EXCEL里的各种奇怪计算问题:数字后面自动多了 0.0001, 数字后面位数变成000,以及一些取整,数学函数
1 公式计算后的数,用只粘贴数值后,后面自动多了 0.0001,导致不再是整数的问题 问题入戏 见第1个8400,计算时就出现了问题,按正常,这里8400应该是整数,而不应该带小数,但是确实就计…...

PHP CRUL请求GET、POST
// GET请求 public function curlGet($url,$header){ $ch curl_init(); curl_setopt($ch, CURLOPT_HTTPHEADER, $header); curl_setopt($ch, CURLOPT_URL, $url); curl_setopt($ch, CURLOPT_SSL_VERIFYPEER, FALSE); curl_setopt($ch, CURLOPT_SSL_VERIFYHOST, FALSE); curl_s…...

Oracle技术分享 exp导数据时报错ORA-01578 ORA-01110
问题描述:exp导数据时报错ORA-01578 ORA-01110,如下所示: 数据库:oracle 19.12 多租户 1、异常重现 [oracledbserver ~]$ exp ora1/ora1orclpdbfileemp.dmp tablesemp logexp.log Export: Release 19.0.0.0.0 - Production onS…...
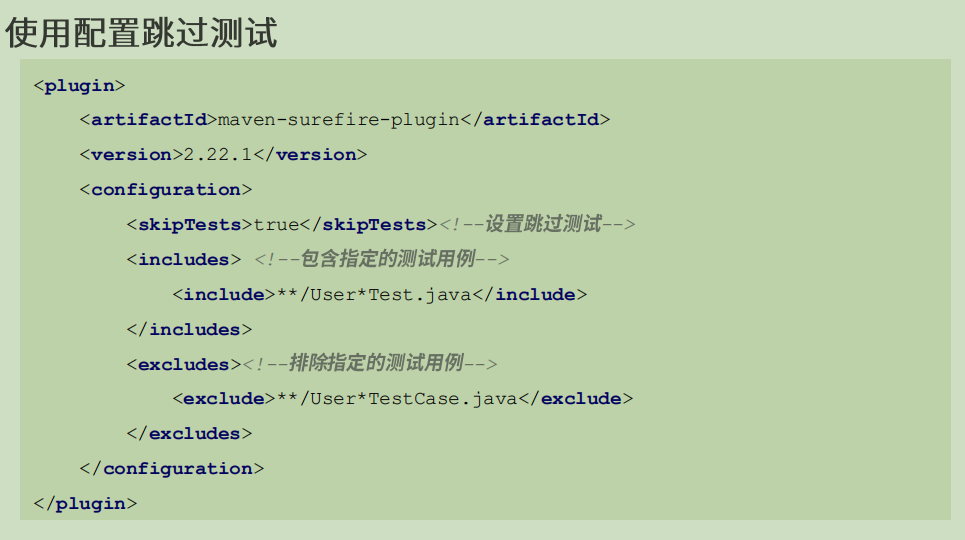
Maven学习笔记
目录1 概述1.1 Maven是什么1.2 作用1.2.1 构建1.3 jar包是什么2 下载及配置2.1 下载2.2 配置环境变量3 基本概念3.1 仓库3.2 坐标3.2.1 概念3.2.2 如何获取指定jar包的坐标3.3 项目结构3.3.1 普通java项目的目录结构3.3.2 java web项目的目录结构3.4 项目构建命令4 IDEA中创建M…...
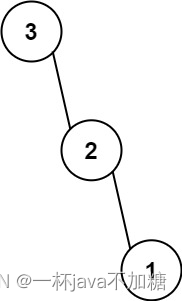
654. 最大二叉树
题目 leetcode题目地址 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建: 创建一个根节点,其值为 nums 中的最大值。 递归地在最大值 左边 的 子数组前缀上 构建左子树。 递归地在最大值 右边 的 子数组后缀上 构建右子树。 返…...
快速幂----快速求解底数的n次幂
目录 一.快速幂 1.问题的引入 2.快速幂的介绍 3.核心思想 4.代码实现 2.猴子碰撞的方法数 1.题目描述 2.问题分析 3.代码实现 一.快速幂 1.问题的引入 问题:求解num的n次幂,结果需要求余7 对于这个问题我们可能就是直接调用函数pow(a,b)来直接求解a的b次幂问题,但是如果…...
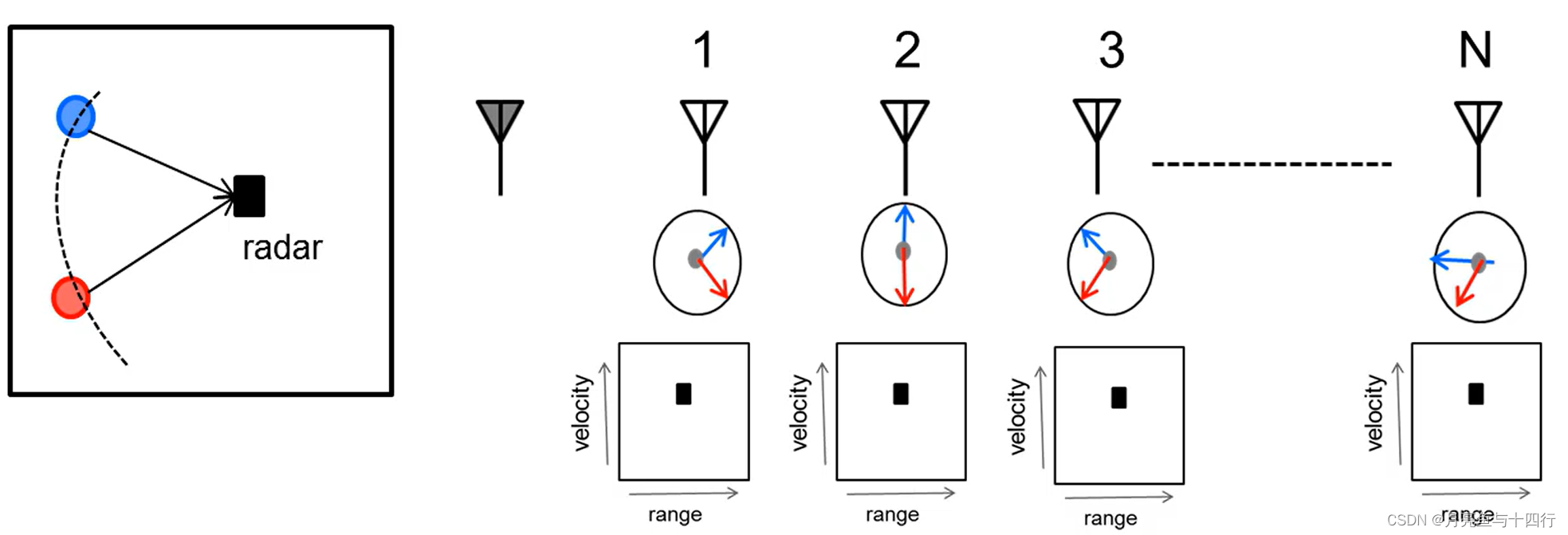
【FMCW 04】测角-Angle FFT
在之前的文章中,我们已经详尽讨论过FMCW雷达测距和测速的原理,现在来讲最后一块内容,测角。测角对于硬件设备具有要求,即要求雷达具有多发多收结构,从而形成多个空间信道(channel),我…...

Linux操作系统学习(线程同步)
文章目录线程同步条件变量生产者与消费者模型信号量环形队列应用生产者消费者模型线程同步 现实生活中我们经常会遇到同一个资源多个人都想使用的问题,例如游乐园过山车排队,玩完的游客还想再玩,最好的办法就是玩完的游客想再玩就去重新排…...

了解动态规划算法:原理、实现和优化指南
动态规划 详细介绍例子斐波那契数列最长回文子串优化指南优化思路斐波那契数列优化最长回文子串优化详细介绍 动态规划(Dynamic Programming,简称 DP)是一种通过将原问题拆分成子问题并分别求解这些子问题来解决复杂问题的算法思想。 它通常用于求解优化问题,它的核心思想…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...
