面试算法-47-有效的括号
题目
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。
示例 1:
输入:s = “()”
输出:true
解
class Solution {public boolean isValid(String s) {LinkedList<Character> stack = new LinkedList<>();for (int i = 0; i < s.length(); i++) {switch (s.charAt(i)) {case '(':stack.push('(');break;case '[':stack.push('[');break;case '{':stack.push('{');break;case ')':if (stack.isEmpty()) {return false;}if (stack.pop() != '(') {return false;}break;case ']':if (stack.isEmpty()) {return false;}if (stack.pop() != '[') {return false;}break;case '}':if (stack.isEmpty()) {return false;}if (stack.pop() != '{') {return false;}break;default:break;}}return stack.isEmpty();}
}
相关文章:

面试算法-47-有效的括号
题目 给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。 有效字符串需满足: 左括号必须用相同类型的右括号闭合。 左括号必须以正确的顺序闭合。 每个右…...

Android11 HID开发系统源码配置
# RK356X_ANDROID11_CUSTOM_HID ## 1.确认SDK版本。 cat .repo/manifests/include/rk356x_repository.xml <?xml version="1.0" encoding="UTF-8"?> <manifest> <project path="device/rockchip/rk356x" name="rk/dev…...

73_Pandas获取分位数/百分位数
73_Pandas获取分位数/百分位数 使用 quantile() 方法获取 pandas 中 DataFrame 或 Series 的分位数/百分位数。 目录 Quantile() 的基本用法指定要获取的分位数/百分位数:参数 q指定interpolation方法:参数interpolation 数据类型 dtype 的差异 指定行…...

力扣练习题
1. 两数之和 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。 你可以按…...

Telegraf--采集指定信息
Telegraf 采集字段解释 根据需求选取需要采集的字段,直接配置在fieldpass中,这样的好处是节约流量,更加简洁明了。下面加粗的部分是telegraf.conf中配置的指标,其他指标根据需求添加即可。 2024年3月18日10:55:41 更新说明: 添加自定义温度指标采集 CPU信息 usage_iowait:…...

Redis是如何实现持久化的?请解释RDB和AOF持久化方式的区别和优缺点。Redis是单线程还是多线程的?为什么Redis使用单线程模型仍然能保持高性能?
Redis是如何实现持久化的?请解释RDB和AOF持久化方式的区别和优缺点。 Redis实现持久化主要有两种方式:RDB(Redis DataBase)和AOF(Append Only File)。这两种方式的主要区别在于它们的持久化机制和适用场景。…...

java通过Excel批量上传数据
一、首先在前端写一个上传功能。 <template><!-- 文件上传 --><el-upload class"upload-demo" :on-change"onChange" :auto-upload"false"><el-button type"primary">上传Excel</el-button></el-up…...
VS2022 配置QT5.9.9
QT安装 下载地址:https://download.qt.io/archive/qt/ 下载安装后进行配置 无法运行 rc.exe 下载VS2022 官网下载 配置 1.扩展-管理扩展-下载Qt Visual Studio Tools 安装 2.安装完成后,打开vs2022,点击扩展,会发现多出了QT VS Tools,点…...
以及输出1-100之间的所有质数)
接收用户输入的数字,判断是否是质数(素数)以及输出1-100之间的所有质数
问题描述:接收用户输入的数字,判断是否是质数(素数)以及输出1-100之间的所有质数 质数的概念:一个大于1的自然数,除了1和它本身外,不能被其他自然数整除的数叫做质数,也称为素数 规定:1既不是…...

人脸识别AI视觉算法---豌豆云
人脸识别AI算法是一种基于计算机视觉和深度学习技术的系统,用于自动识别和验证人脸。 这些算法在多种领域有着广泛的应用,包括安全认证、身份验证、监控、社交媒体、医疗保健和零售等。 以下是有关人脸识别AI算法的技术背景和应用场景的介绍࿱…...

Apache SeaTunnel MongoDB CDC 使用指南
随着数据驱动决策的重要性日益凸显,实时数据处理成为企业竞争力的关键。SeaTunnel MongoDB CDC(Change Data Capture) 源连接器的推出,为开发者提供了一个高效、灵活的工具,以实现对 MongoDB 数据库变更的实时捕获和处理。 本文将深入探讨该连…...
智能合约 之 部署ERC-20
Remix介绍 Remix是一个由以太坊社区开发的在线集成开发环境(IDE),旨在帮助开发者编写、测试和部署以太坊智能合约。它提供了一个简单易用的界面,使得开发者可以在浏览器中直接进行智能合约的开发,而无需安装任何额外的…...
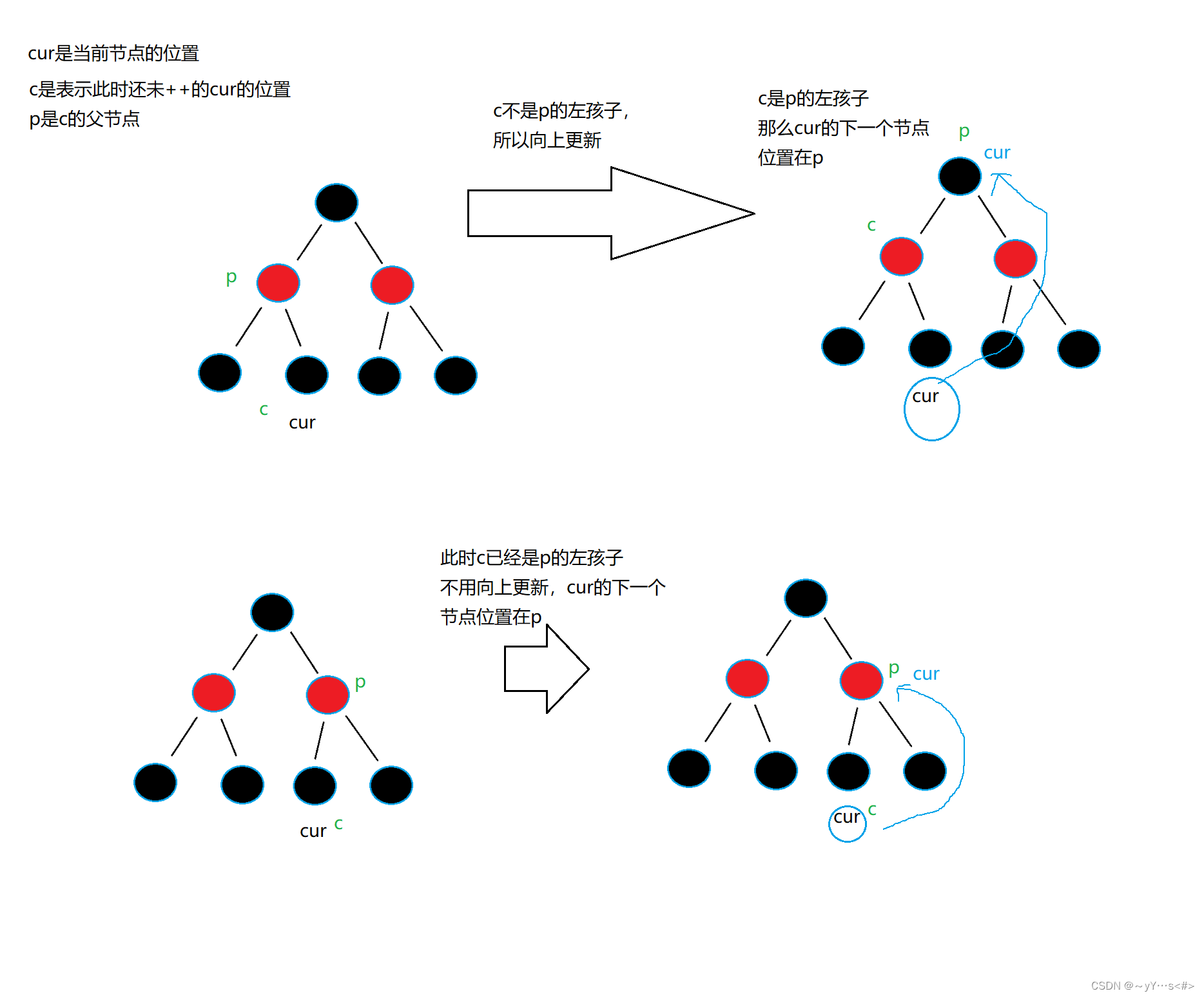
【C++】用红黑树模拟实现set、map
目录 前言及准备:一、红黑树接口1.1 begin1.2 end1.3 查找1.4 插入1.5 左单旋和右单旋 二、树形迭代器(正向)2.1 前置 三、模拟实现set四、模拟实现map 前言及准备: set、map的底层结构是红黑树,它们的函数通过调用红…...

实现:mysql-5.7.42 到 mysql-8.2.0 的升级(二进制方式)
实现:mysql-5.7.42 到 mysql-8.2.0 的升级(二进制方式) 1、操作环境1、查看当前数据库版本2、操作系统版本3、查看 Linux 系统上的 glibc(GNU C 库)版本(**这里很重要,要下载对应的内核mysql版本…...

深入探讨医保购药APP的技术架构与设计思路
随着移动互联网的发展,医疗保健行业也迎来了数字化转型的浪潮。医保购药APP作为医保体系数字化的一部分,其技术架构和设计思路至关重要。接下来,小编将为您讲解医保购药APP的技术架构与设计思路,为相关从业者提供参考和启发。 一、…...

react中点击按钮不能获取最新的state时候
在这个问题中,用户希望在点击确认按钮时触发handleChange函数,并且能够正确获取到最新的bzText值。最初的代码中,在handleOpen函数中弹出一个确认框,并在确认框的onOk回调函数中调用handleChange函数。然而,由于组件传…...
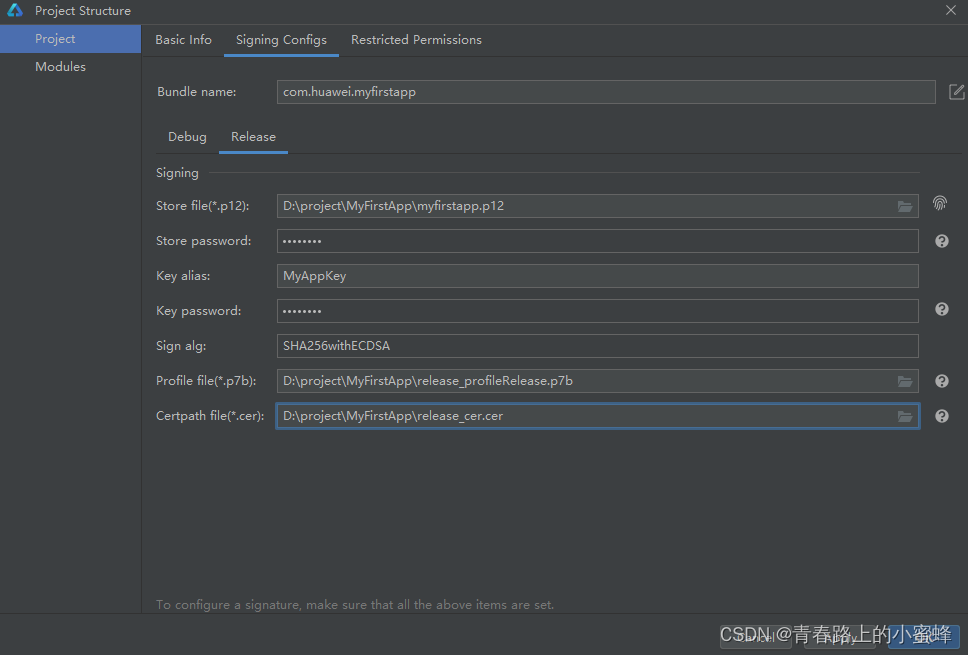
2、鸿蒙学习-申请调试证书和调试Profile文件
申请发布证书 发布证书由AGC颁发的、为HarmonyOS应用配置签名信息的数字证书,可保障软件代码完整性和发布者身份真实性。证书格式为.cer,包含公钥、证书指纹等信息。 说明 请确保您的开发者帐号已实名认证。每个帐号最多申请1个发布证书。 1、登录AppGa…...
:十大排序算法(希尔排序) (快速排序)c语言版)
蓝桥杯算法基础(13):十大排序算法(希尔排序) (快速排序)c语言版
希尔排序 优化版的插入排序,优化的地方就是步长(增量)增大了,原来的插入排序的步长(增量)是1,而希尔排序的步长(增量)可以很大,然后逐渐减小直到1形成插入排…...
)
web学习笔记(三十二)
目录 1.函数的call、apply、bind方法 1.1call、apply、bind的相同点 1.2call、apply、bind的不同点 1.3call、apply、bind的使用场景 2. 对象的深拷贝 2.1对象的浅拷贝 2.1对象的深拷贝 1.函数的call、apply、bind方法 1.1call、apply、bind的相同点 在没有传参数时&…...

Android 地图SDK 绘制点 删除 指定
问题 Android 地图SDK 删除指定绘制点 详细问题 笔者进行Android 项目开发,对于已标记的绘制点,提供撤回按钮,即删除绘制点,如何实现。 解决方案 新增绘制点 private List<Marker> markerList new ArrayList<>…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...
