LeetCode096不同的二叉搜索树(相关话题:卡特兰数)
目录
题目描述
解题思路
代码实现
进出栈序列理解卡特兰数分析策略
相关知识
参考文章
题目描述
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:

输入:n = 3 输出:5
示例 2:
输入:n = 1 输出:1
解题思路
题目要求是计算不同二叉搜索树的个数。为此,我们可以定义两个函数:
G(n): 长度为 n 的序列能构成的不同二叉搜索树的个数。
F(i,n) 以 i为根、序列长度为 n 的不同二叉搜索树个数 (1≤i≤n)。
可见,G(n) 是我们求解需要的函数。
稍后我们将看到,G(n)可以从 F(i,n)得到,而 F(i,n)又会递归地依赖于 G(n)。
首先,根据上一节中的思路,不同的二叉搜索树的总数 G(n),是对遍历所有 i (1≤i≤n)的 F(i,n) 之和。换言之:
公式一
对于边界情况,当序列长度为 1(只有根)或为 0(空树)时,只有一种情况,即:
G(0)=1,G(1)=1
给定序列 1⋯n,我们选择数字 i 作为根,则根为 i的所有二叉搜索树的集合是左子树集合和右子树集合的笛卡尔积,对于笛卡尔积中的每个元素,加上根节点之后形成完整的二叉搜索树,如下图所示:
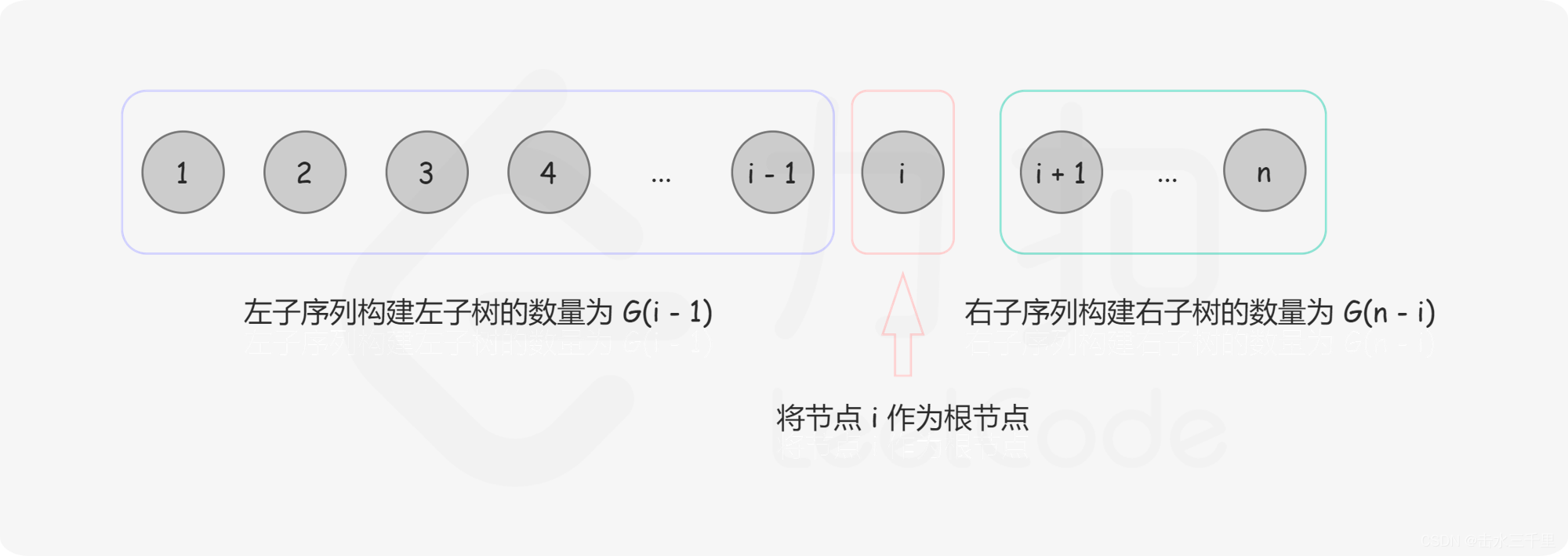
因此,我们可以得到以下公式:
公式二
F(i,n)=G(i−1)⋅G(n−i)
将公式一二 结合,可以得到 G(n的递归表达式:
事实上我们在方法一中推导出的 G(n)函数的值在数学上被称为卡塔兰数
卡塔兰数更便于计算的定义如下:
代码实现
class Solution {public int numTrees(int n) {int[] G = new int[n + 1];G[0] = 1;G[1] = 1;for (int i = 2; i <= n; ++i) {for (int j = 1; j <= i; ++j) {G[i] += G[j - 1] * G[i - j];}}return G[n];}
}进出栈序列理解卡特兰数分析策略
这是一道最经典的入门级卡特兰数题目,如果能把这题看懂,相信后面的题目也能迎刃而解。
题目
n 个元素进栈序列为:1,2,3,4,...,n,则有多少种出栈序列?
思路
我们将进栈表示为 +1,出栈表示为 -1,则 1 3 2 的出栈序列可以表示为:+1 -1 +1 +1 -1 -1。

根据栈本身的特点,每次出栈的时候,必定之前有元素入栈,即对于每个 -1 前面都有一个 +1 相对应。因此,出栈序列的所有前缀和必然大于等于 0,并且 +1 的数量等于 -1 的数量。
接下来让我们观察一下 n = 3 的一种出栈序列:+1 -1 -1 +1 -1 +1。序列前三项和小于 0,显然这是个非法的序列。
如果将第一个前缀和小于 0 的前缀,即前三项元素都进行取反,就会得到:-1 +1 +1 +1 -1 +1。此时有 3 + 1 个 +1 以及 3 - 1 个 -1。
因为这个小于 0 的前缀和必然是 -1,且 -1 比 +1 多一个,取反后,-1 比 +1 少一个,则 +1 变为 n + 1 个,且 -1 变为 n - 1 个。进一步推广,对于 n 元素的每种非法出栈序列,都会对应一个含有 n + 1 个 +1 以及 n - 1 个 -1 的序列。
如何证明这两种序列是一一对应的?
假设非法序列为 A,对应的序列为 B。每个 A 只有一个"第一个前缀和小于 0 的前缀",所以每个 A 只能产生一个 B。而每个 B 想要还原到 A,就需要找到"第一个前缀和大于 0 的前缀",显然 B 也只能产生一个 A。
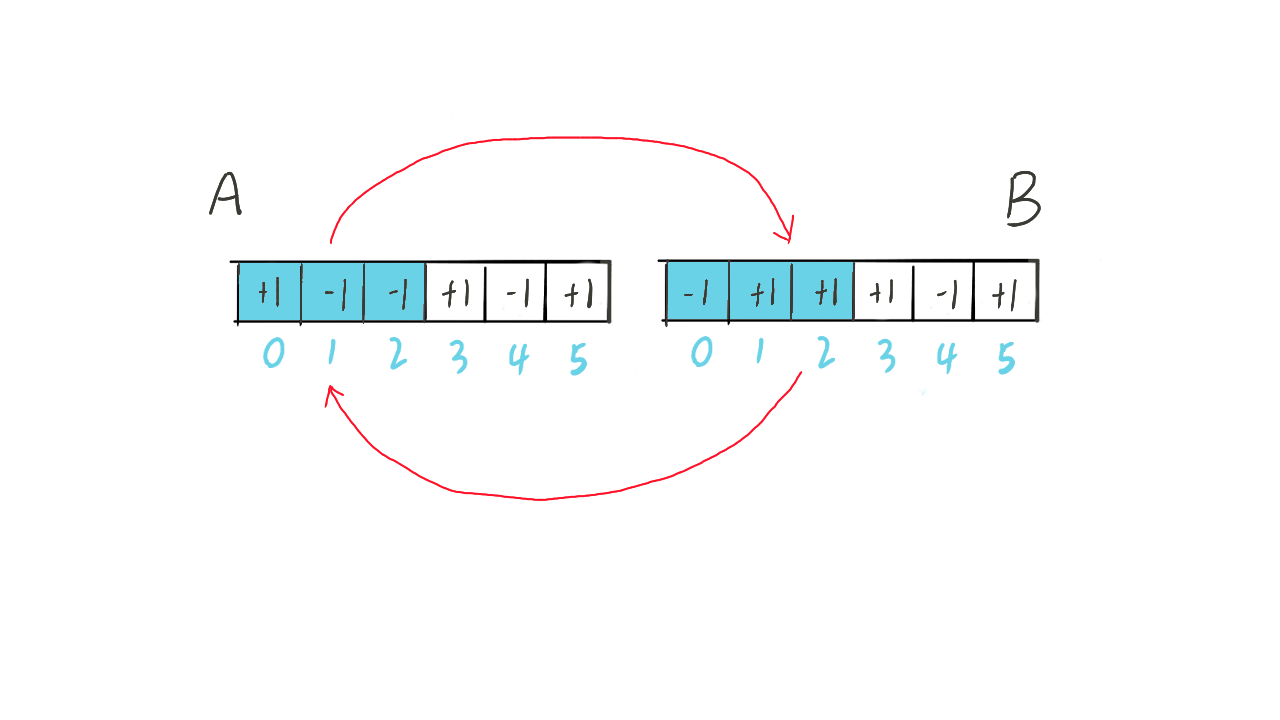
每个 B 都有 n + 1 个 +1 以及 n - 1 个 -1,因此 B 的数量为 相当于在长度为 2n 的序列中找到
n + 1 个位置存放 +1。相应的,非法序列的数量也就等于。
出栈序列的总数量共有,因此,合法的出栈序列的数量为
此时我们就得到了卡特兰数的通项
相关知识
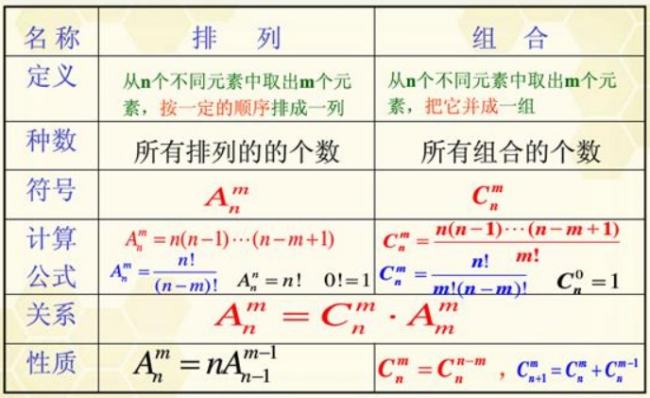
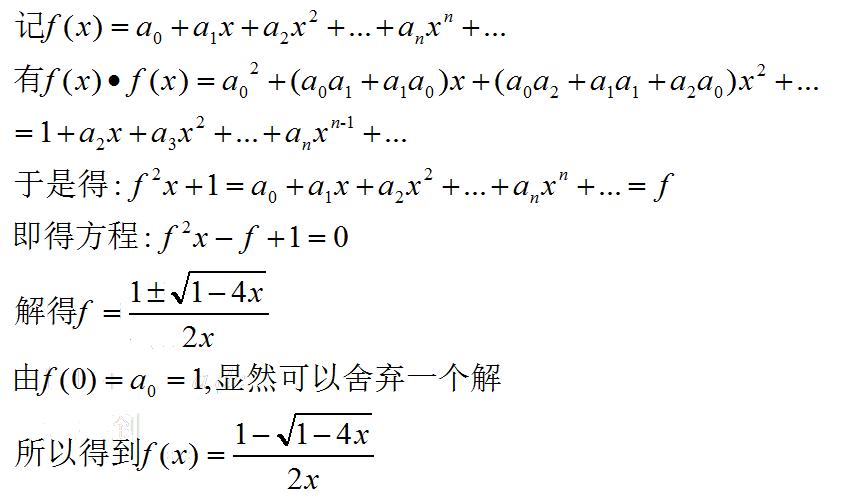
顺便提一下,这里f(0)=1,
但是看表达式的话x=0是没定义的,
所以这里是极限意义上的,
然后补充该点定义即可,
再详细的细节就不深究了...
可以验证极限是否是1:
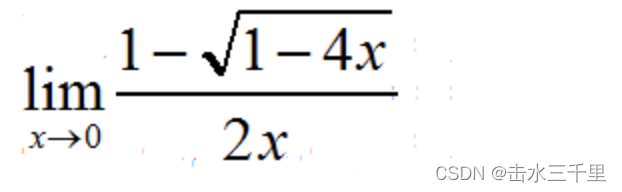
令1-4x=t 那么
当 时 的泰勒展开公式:
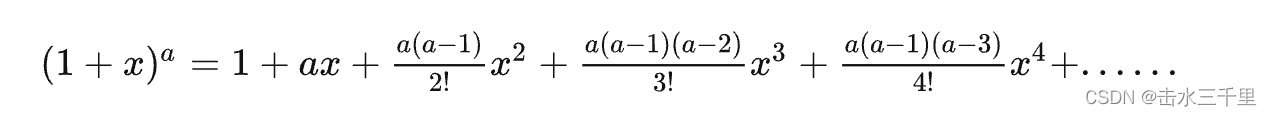

这个通项看起来太不和谐了,
还是再整理一下吧:
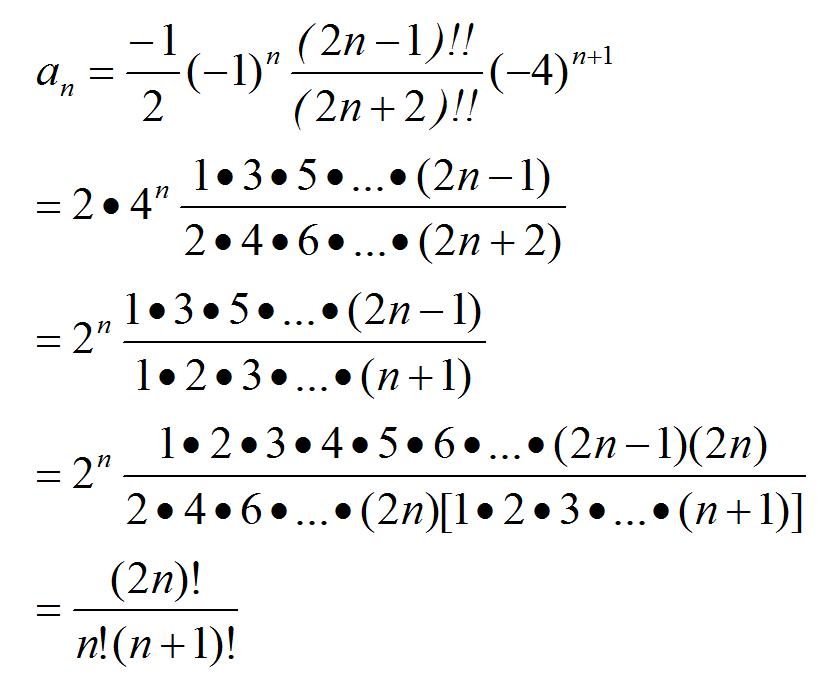
参考文章
由递推式求catalan数列通项公式
「算法入门笔记」卡特兰数
不同的二叉搜索树
相关文章:
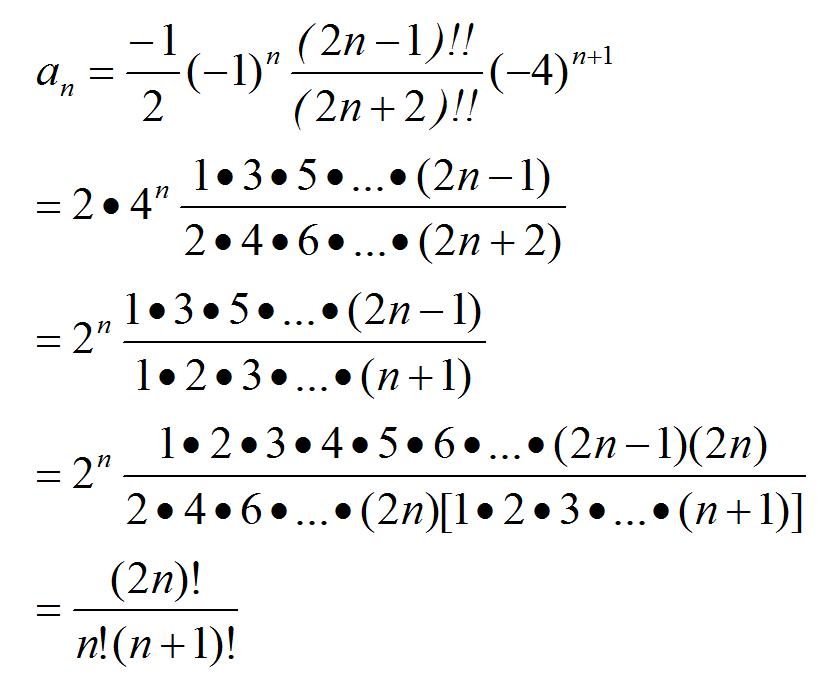
LeetCode096不同的二叉搜索树(相关话题:卡特兰数)
目录 题目描述 解题思路 代码实现 进出栈序列理解卡特兰数分析策略 相关知识 参考文章 题目描述 给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。 示例 1: …...
软件测试7
一 CS和BS软件架构 CS:客户端-服务器端,BS:浏览器端-服务器端 区别总结: 1.效率:c/s效率高,某些内容已经安装在系统中了,b/s每次都要加载最新的数据 2.升级:b/s无缝升级,…...
12 结构:如何系统设计框架的整体目录?
到现在,我们已经将 Gin 集成到框架 hade 中,同时又引入了服务容器和服务提供者,明确框架的核心思想是面向服务编程,一切皆服务,所有服务都是基于协议。后续也会以服务的形式,封装一个个的服务,让…...
假如你知道这样的MySQL性能优化
1. 为查询缓存优化你的查询 大多数的 MySQL 服务器都开启了查询缓存。这是提高性最有效的方法之 一,而且这是被 MySQL 的数据库引擎处理的。当有很多相同的查询被执行了多次的时候,这些查询结果会被放到一个缓存中,这样,后续的相同…...
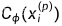
79、ClimateNeRF: Physically-based Neural Rendering for Extreme Climate Synthesis
简介主页物理模拟可以很好地预测天气影响。神经辐射场产生SOTA场景模型。ClimateNeRF 允许我们渲染真实的天气效果,包括雾霾、雪和洪水 ,结果可以通过有物理意义的变量来控制,比如水位 ,这允许人们可视化气候变化的结果将对他们产…...
)
前端面试题(一)
目录 前言 一、css3实现布局的方式有哪些? 1.flex布局 2.grid布局 二、jquery的扩展机制? 三、jquery动画和css实现动画的本质区别? 四、不使用css的动画,如何实现盒子从左到右移动? 五、使用过的框架…...

Java基础常见面试题(七)
序列化和反序列化 Java序列化与反序列化是什么? Java序列化是指把Java对象转换为字节序列的过程,而Java反序列化是指把字节序列恢复为Java对象的过程。 序列化: 序列化是把对象转换成有序字节流,以便在网络上传输或者保存在本地…...

【springmvc】报文信息转换器
HttpMessageConverter HttpMessageConverter,报文信息转换器,将请求报文转换为Java对象,或将Java对象转换为响应报文 HttpMessageConverter提供了两个注解和两个类型: RequestBody, ResponseBody, Reques…...

3.5知识点复习
extern:表示声明。 没有内存空间。 不能提升。const:限定一个变量为只读变量。volatile:防止编译器优化代码。volatile int flg 0; register:定义一个寄存器变量。没有内存地址。register int a 10;字符串:C语言中&a…...

湖南中创教育PMP分享项目经理有哪些优势?
项目经理拥有超强的计划能力;具备大局意识;沟通能力特别强;具备更大的灵活性和反应能力以及总结汇报能力 1、超强的计划能力 项目经理几乎无时无刻都在做计划,因此也就更擅长做计划。 项目管理要抓重点,有主次地处理…...

LeetCode:27. 移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。 不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。 元素的顺序可以改变。你不需要考虑数组中超出新长度后面…...
麻雀算法SSA优化LSTM长短期记忆网络实现分类算法
1、摘要 本文主要讲解:麻雀算法SSA优化LSTM长短期记忆网络实现分类算法 主要思路: 准备一份分类数据,数据介绍在第二章准备好麻雀算法SSA,要用随机数据跑起来用lstm把分类数据跑起来将lstm的超参数交给SSA去优化优化完的最优参数…...

哈希表题目:数组中的 k-diff 数对
文章目录题目标题和出处难度题目描述要求示例数据范围解法思路和算法代码复杂度分析题目 标题和出处 标题:数组中的 k-diff 数对 出处:532. 数组中的 k-diff 数对 难度 4 级 题目描述 要求 给定一个整数数组 nums\texttt{nums}nums 和一个整数 k…...
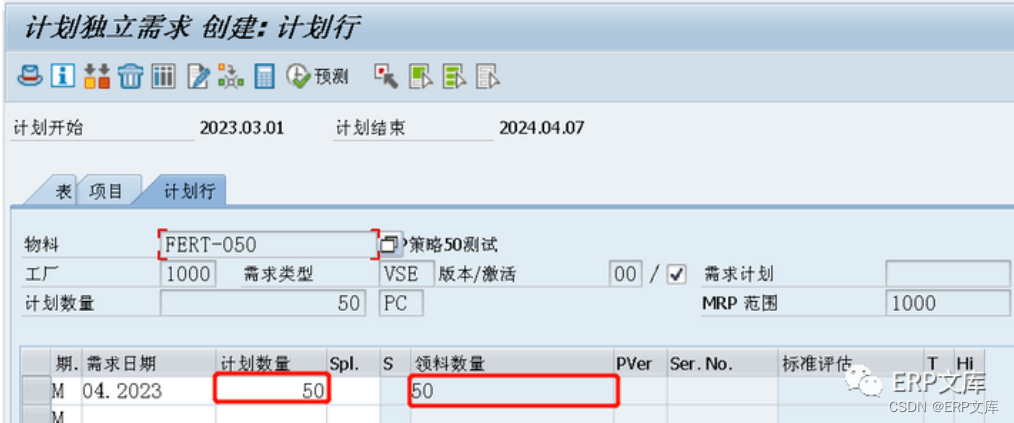
SAP ERP系统PP模块计划策略2050详解
SAP/ERP系统中面向订单生产的计划策略主要有20和50两个策略,这两个策略都是面向订单生产的计划策略,也是离散制造行业应用比较广泛的策略。它们之间最大差异就是在于20策略完全是由订单驱动,而50策略是预测加订单驱动,本文主要介绍…...

TIA博途中将硬件目录更改为中文的具体方法演示
TIA博途中将硬件目录更改为中文的具体方法演示 基本步骤可参考如下: 第一步: 第二步: 具体的操作演示: 如下图所示,在所示的目录中找到zh-chs文件夹,删除或修改文件夹的名称均可,这里建议大家修改文件夹的名称,防止以后需要恢复成英文目录, 如下...

【多线程操作】线程池模拟实现
目录 一.线程池的作用 二.线程池的模拟实现 1.线程模块(Thread.hpp): 2.线程锁模块(LockGuard.hpp): 3.任务模块(Task.hpp) 4.线程池核心(ThreadPool.hppÿ…...
HBase---Hbase安装(单机版)
Hbase安装单机版 文章目录Hbase安装单机版Master/Slave架构安装步骤配置Hbase1.上传压缩包解压更名修改hbase-env.sh修改hbase-site.xml配置HBase环境变量配置Zookeeper复制配置文件修改zoo.cfg配置文件修改myid配置Zookeeper环境变量刷信息配置文件启动hbase步骤hbase shellMa…...
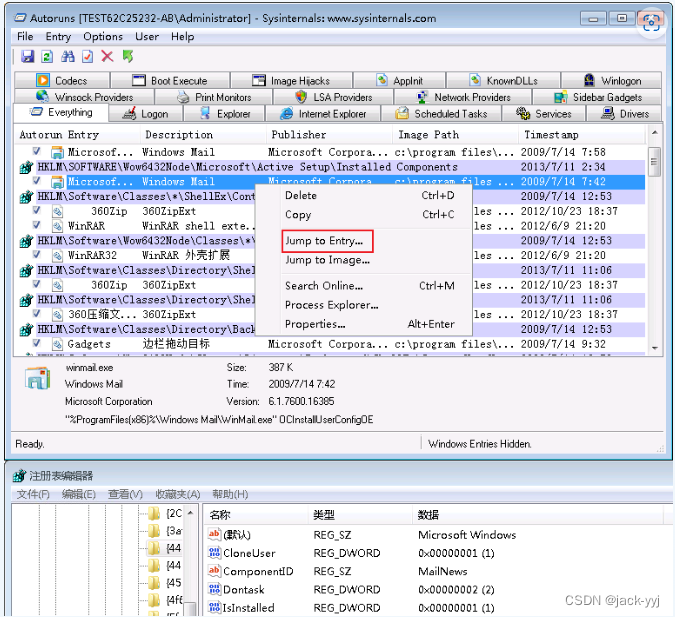
启动项管理工具Autoruns使用实验(20)
实验目的 (1)了解注册表的相关知识; (2)了解程序在开机过程中的自启动; (3)掌握Autoruns在注册表和启动项方面的功能;预备知识 注册表是windows操作系统中的一个核心数据…...

BFD单臂回声实验详解
13.1.1BFD概念 BFD提供了一个通用的、标准化的、介质无关的、协议无关的快速故障检测机制,有以下两大优点: 对相邻转发引擎之间的通道提供轻负荷、快速故障检测。 用单一的机制对任何介质、任何协议层进行实时检测。 BFD是一个简单的“Hello”协议。两个系统之间建立BFD会…...
详解JAVA类加载器
目录 1.概述 2.双亲委派 3.ServiceClassLoader 4.URLClassLoader 5.加载冲突 1.概述 概念: 类加载器(Class Loader)是Java虚拟机(JVM)的一个重要组件,负责加载Java类到内存中并使其可以被JVM执行。类…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

