球面数据的几何深度学习--球形 CNN
目录
- 一、说明
- 二、球形 CNN概述
- 三、球面数据的对称性
- 四、标准(平面)CNN的局限性
- 五、卷积并发症
- 六、球面卷积
- 七、球面卷积是不够的

一、说明
球面数据的几何深度学习–球形 CNN。通过对物理世界的平移对称性进行编码,卷积神经网络 (CNN) 彻底改变了计算机视觉。
二、球形 CNN概述
在这篇博文中,我们研究了如何将CNN成功的基本原理转移到数据表现出复杂几何形状的问题范围,例如球体。
这篇博文由来自 Kagenova 的 Oliver Cobb 和 Augustine Mavor-Parker 共同撰写。
球面数据示例。[照片由 NASA 在 Unsplash 上拍摄]
T在过去十年中,CNN从传统(平面)图像和视频中提取语义意义的能力得到了迅速提高。如果有足够的数据,通常可以达到人类水平的性能。然而,对具有空间结构的数据进行分析远未解决问题。对于各种问题,数据表现出空间结构,但非平面结构。示例包括虚拟现实中的 360° 图像、来自宇宙大爆炸的宇宙微波背景 (CMB) 辐射、医学成像中的 3D 扫描以及计算机图形学中的网格表面,仅举几例。
对于这些问题中的每一个,我们都希望利用我们对数据结构的了解,特别是它们所遵循的对称性变换。正如在之前的博客文章中所讨论的,将对称性的理解编码到机器学习模型中可以成为限制所考虑模型空间的有效方法,从而可以更有效地学习模型。
对于平面上的图像,通过应用一堆卷积滤波器,可以在图像上平移,从而轻松有效地对平移对称性进行编码。由于在所有位置都应用了相同的卷积滤波器,因此结果操作是平移等变的,即它尊重平移对称性。这意味着无论特征位于图像中的哪个位置,它都会以相同的方式刺激相应位置的激活神经元。
不幸的是,对于非平面结构的问题,通常不存在这种简单的程序来编码对起作用的对称性的理解。然而,对于这些问题,新兴的几何深度学习领域的研究人员正在制定新的方法,这些方法利用了数据几何形式的属性,并尊重了起作用的对称性。最近取得重大进展的一系列问题是那些在球体表面上定义数据的问题。
三、球面数据的对称性
许多字段都涉及固存在于球体上的数据。
在球面上的每个点进行观测时,例如地球的地形图,可能会产生球面数据。然而,当对方向进行观测时,例如宇宙学中的宇宙微波背景 (CMB) 或虚拟现实和计算机视觉中的 360° 图像(见下图),也会出现这种情况。在Kagenova,我们正在努力解决深度学习在这些问题和其他涉及复杂几何数据(如球体)方面取得的巨大成功。

Examples of spherical data. [Original figure created by authors.]
对于平面图像,CNN 规定定义特定特征如何变换的规则不应依赖于特征恰好位于平面中的位置。对于在球体上定义的数据,我们希望规定规则不应取决于要素在球体上的方向和位置。变换特征,然后旋转其变换形式应等同于旋转特征并变换其旋转形式。关于此属性的操作被称为旋转等变的(见下图)。
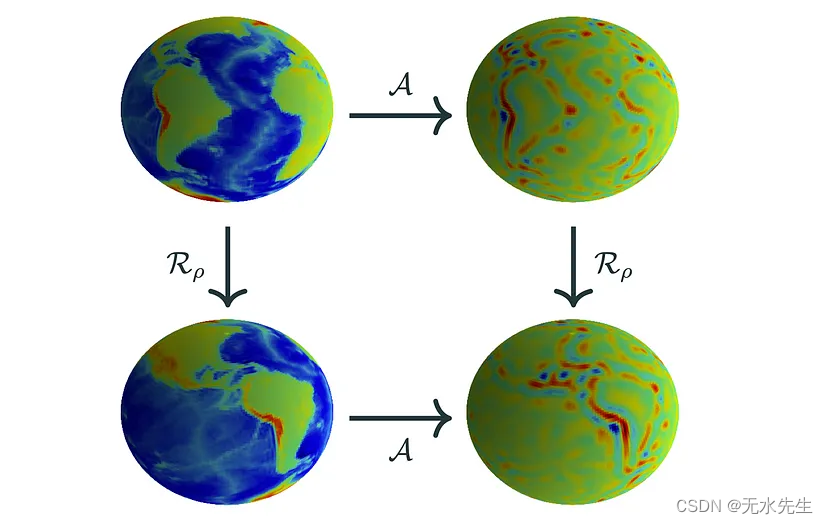
旋转等方差的图示。给定球面数据(左上),应用变换 (A) 获得特征图(右上),然后旋转 (Rρ) 特征图(右下)等效于先旋转数据(左下)然后应用变换(右下)。[作者创作的原始数字。]
在物理学中,规定控制系统行为的物理定律不应取决于系统的方向,从而产生了角动量守恒定律。因此,毫不奇怪,量子物理学中用于研究角动量的一些相同机制可用于定义深度学习中的旋转等变层(我们将在后面看到)。
四、标准(平面)CNN的局限性
在深入研究球形深度学习的想法之前,也许很自然地想知道为什么不能直接利用平面 CNN 的有效性。我们能不能不能将球面数据投射到某个平面表示上,而简单地以通常的方式应用CNN?毕竟,我们熟悉球形世界的平面投影(地图)。
投影的问题在于,不存在从球体到平面的投影,它同时保留了形状和面积。换句话说,扭曲是不可避免的。
这就是为什么格陵兰岛在地球地图上通常看起来与非洲相似,而实际上它的大小不到非洲的十分之一(见下图)。
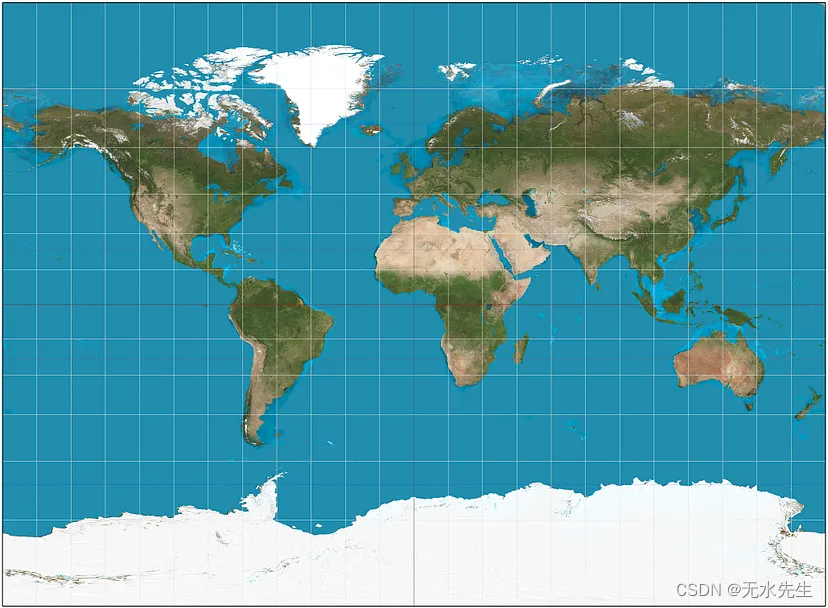
球体到平面的投影会引入不可避免的变形,与所使用的投影方法无关。出于这个原因,格陵兰岛在地球地图上通常看起来与非洲相似,但实际上还不到非洲的十分之一。[图片来自Wikimedia Commons。
这些失真意味着,当将传统CNN应用于球形图像的平面投影时,特征的显示方式会根据它们所在的位置而有所不同。当应用于球面图像的平面投影时,平面 CNN 的平移等方差不会编码旋转等方差。编码旋转等方差需要一个专门为球体几何形状设计的卷积概念。
五、卷积并发症
不幸的是,平面 CNN 实现的简单卷积过程不能应用于球形设置。
要了解为什么会这样,首先考虑平面数据的形式。平面数据表示为像素值的 2D 数组。对于在平面上定义的数据,我们可以在水平和垂直方向上均匀地划分像素位置。平面的这种统一采样意味着每个像素都有关联的邻居,并且所有像素的邻居位于相同的相对位置(北、东北、东等)。这意味着,通过平移,在相同采样位置定义的任何滤波器都可以以输入中的任何像素为中心,从而使样本完全对齐。
不幸的是,没有办法对球体进行采样,使所有像素的邻居都处于相同的相对位置。球体上的位置通常使用球面坐标来描述,θ 测量极角,φ测量方位角。相对于 θ 和 φ 均匀间隔样品可得到下图左侧所示的球体采样。如果我们使用这些采样位置来定义过滤器,然后旋转过滤器,我们会发现样本位置不对齐(见下图)。无论我们如何选择对球体进行采样,这都是正确的。

假设我们使用与球面数据相同的样本位置来定义一个过滤器。这样就不可能评估滤波器在各种旋转下与数据的匹配程度,因为样本不对齐。对于球体的所有采样都是如此。[原创图由作者创作。
众所周知,不可能以不变于旋转的方式离散球体。因此,不可能构造一个严格旋转等变的纯离散球面卷积。
为了构造一个捕捉旋转等方差所需性质的卷积球形概念,我们必须考虑连续表示。值得庆幸的是,存在这样一种表示,可以执行自然的卷积概念。
考虑球体上连续信号的表示。这些是函数 f:S² → R,将值与球体 S² 上的每个点 (θ, φ) 相关联,而不仅仅是在选定的样品位置。正如圆上的连续信号(即周期函数)可以分解为正弦和余弦函数的加权和一样,球面上的连续信号也可以类似地分解为谐波基信号的加权和(见下图)。在这两种情况下,都可以使用权重(系数)来表示信号,从而产生圆上信号的傅里叶级数表示和球面上信号的球谐表示。
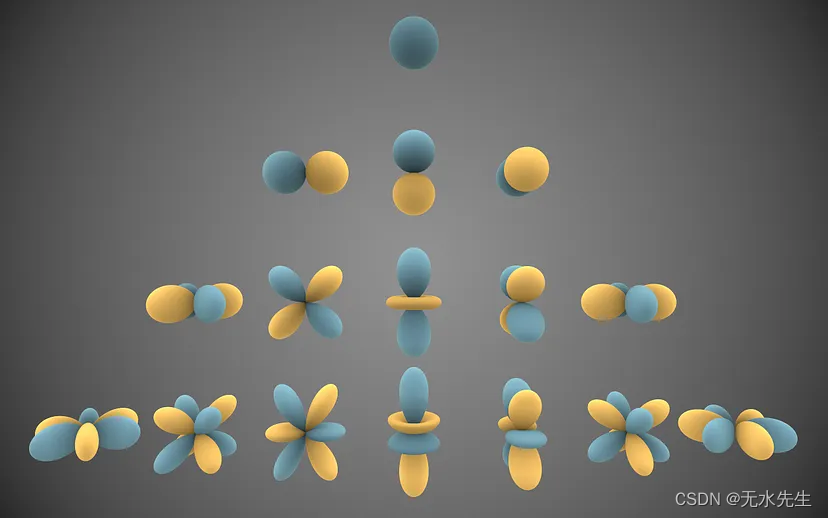
球谐波函数。[图片来自Wikimedia Commons。
尽管这种表示是无限的,但通过适当地截断系数向量,可以非常准确地近似真实世界的信号。从上图中我们可以看到,低度球谐波只能捕获低频变化,而高度球谐波可以捕获较高频率的变化。我们截断的点决定了数据表示的分辨率。
六、球面卷积
回想一下,我们想对满足旋转等方差性质的球面数据进行变换。
有一个非常自然的球面卷积概念,在连续设置中类似于在平面情况下执行的卷积。
这是取球面信号 f:S² → R,定义一个球面滤波器 g:S² → R,并计算由
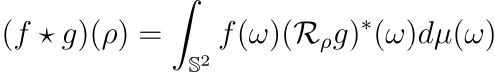
这里我们使用了旋转算子 Rρ,定义为 (Rρ g)(ω)=g(ρ⁻¹ω)。换句话说,它具有将相应的反向旋转应用于函数域的效果,类似于我们如何看待平移在一维线或二维平面上定义的函数。
上述等式的解释是,卷积信号 f * g 捕获了在任何给定旋转 ρ 下滤波器 g 与信号 f 的匹配程度(见下图)。这类似于平面情况,在平面情况下,我们考虑滤波器在各种转换下与输入的匹配程度。

使用滤波器(中)可视化数据的球面卷积(左)以生成特征图(右)。[原创图由作者创作。
这里的主要区别在于,定义卷积信号的空间,即旋转的空间(3D 空间),与定义卷积信号和滤波器的空间(2D 球体)不同。在上面所示的说明性示例中,滤波器不变于方位角旋转,因此输出保持在球体上。
然而,将输入信号从球体提升到 3D 旋转空间并不是特别成问题。随后可以在旋转空间上定义的信号和滤波器之间执行类似的卷积概念。因此,给定一个球面输入,为了分层学习特征,我们可以执行一个球面卷积,从而在 3D 旋转组上生成激活图,然后根据需要进行任意数量的旋转组卷积。
要了解为什么上述卷积概念是旋转等变的,请注意,将输入旋转 ρ 等同于对积分内部的滤波器施加额外的 ρ⁻¹ 旋转。反过来,这又具有旋转由 ρ⁻¹ 定义卷积信号的域的效果。换句话说,在执行卷积之前旋转输入等同于执行卷积,然后旋转输出。
两个球面信号的卷积似乎需要为三维空间中的每个值计算一个二维积分。然而,幸运的是,f * g 的谐波表示与 f 和 g 的谐波表示之间的关系很简单。球面卷积可以通过在 f 的谐波系数和 g 的谐波系数之间进行矩阵乘法来计算谐波空间。鉴于深度学习从业者习惯于利用 GPU 有效地执行矩阵乘法,这特别方便。
七、球面卷积是不够的
配备了可以有效实现的旋转等变线性操作,我们似乎拥有重复应用此操作并分层学习特征所需的一切。
然而,到目前为止,我们忽略了一个重要的组成部分——非线性的引入。
在平面网络中,非线性是由逐点激活函数引入的,即通过将选定的非线性函数分别应用于每个样本位置的值。由于平面采样方案的均匀性,这确实是一种平移等变操作。但是,我们已经过渡到使用没有关联样本位置或值的谐波表示。尽管可以获得基于样本的表示,但我们无法均匀地对球体进行采样(如上所述),这意味着对每个样本应用相同的非线性函数并不是严格意义上的旋转等变操作。
然而,以这种方式引入非线性是可能的,并且正如Cohen等人(2018)和Esteves等人(2018)所表明的那样,通常相当有效。然而,为了执行卷积和非线性运算,在谐波和基于样本的表示之间反复转换是很麻烦的。此外,人们很自然地想知道失去的等价方差在多大程度上阻碍了性能。
在我们的下一篇文章中,我们将看到如何利用量子物理学的思想直接在谐波空间中引入非线性,而不会影响我们对旋转对称性的尊重程度。
引用
[1] Cohen,Geiger,Koehler,Welling,球形CNNs,ICLR(2018),arxiv:1801.10130。
[2] Esteves、Allen-Blanchette、Makadia、Daniilidis,使用球形 CNN 学习 SO(3) 等变表示,ECCV (2018),arXiv:1711.06721。
相关文章:

球面数据的几何深度学习--球形 CNN
目录 一、说明二、球形 CNN概述三、球面数据的对称性四、标准(平面)CNN的局限性五、卷积并发症六、球面卷积七、球面卷积是不够的 一、说明 球面数据的几何深度学习–球形 CNN。通过对物理世界的平移对称性进行编码,卷积神经网络 ࿰…...
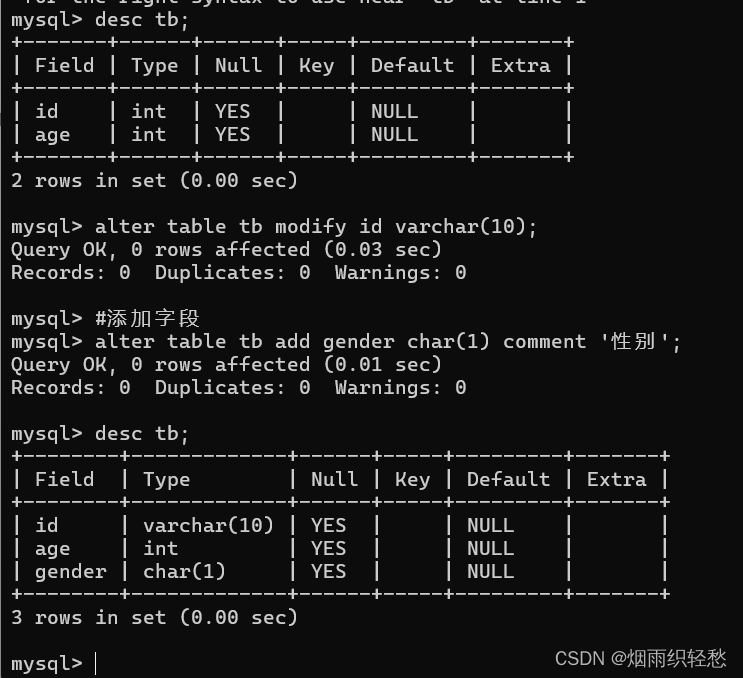
MySQL学习笔记------SQL(1)
关系型数据库(RDBMS) 建立在关系模型基础上,由多张相互连接的二维表组成的数据库 特点:使用表储存数据,格式统一,便于维护 使用SQL语言操作,标准统一,使用方便 SQL通用语法 SQL…...

PMP能提前查成绩?还能改分数?别太离谱!
震惊!3月10日PMP考试才结束没多久,昨天就有学员收到了查分邮件,寄信人自称自己是内部人员,可以提前查询到成绩并直接修改成绩。 这也太离谱了吧!在此,小赛想说,PMP考试是一个公正、严格的考试体…...

【保姆级讲解服务器硬件的基础知识】
服务器硬件基础知识 1. 前言2. 中央处理器(CPU)3. 内存(RAM)4. 存储设备5. 主板6. 电源供应单元(PSU)7. 冷却系统8. 网络连接9. 扩展插槽和端口10. 管理功能 🌈🌈🌈&…...

并查集---力扣547省份的数量
假设:有一群小混混打架,小弟们可能互相不认识,如果要确定他们是一伙的,就需要确定他们的组长是不是一个,但是每个组长的领导可能又不一样,所以要找到最大的那个领导,才能确定是一伙的。 我们先…...
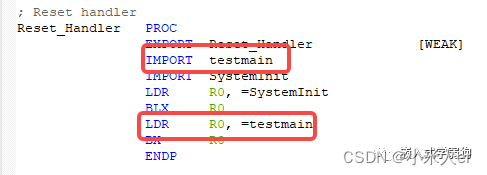
stm32启动文件里面的__main和主函数main()
一、__main和main()之间的关系 先来对stm32启动过程简单学习 启动文件里面的Reset_Handler: 调用过程: stm32在启动后先进入重启中断函数Reset_Handler,其中会先后调用SystemInit和__main函数, __main函数属于c库函数&…...

曲线生成 | 图解Reeds-Shepp曲线生成原理(附ROS C++/Python/Matlab仿真)
目录 0 专栏介绍1 什么是Reeds-Shepp曲线?2 Reeds-Shepp曲线的运动模式3 Reeds-Shepp曲线算法原理3.1 坐标变换3.2 时间翻转(time-flip)3.3 反射变换(reflect)3.4 后向变换(backwards) 4 仿真实现4.1 ROS C实现4.2 Python实现4.3 Matlab实现 0 专栏介绍 ǵ…...
深入探讨iOS开发:从创建第一个iOS程序到纯代码实现全面解析
iOS开发作为移动应用开发的重要领域之一,对于开发人员具有重要意义。本文将深入探讨iOS开发的各个方面,从创建第一个iOS程序到纯代码实现iOS开发,带领读者全面了解iOS应用程序的开发流程和技术要点。 📱 第一个iOS程序 在创建第…...

Python学习之-正则表达式
目录 前言:1.re.serach1.1例子: 2.re.match2.1示例1:2.2 示例2: 3.re.findall3.1 示例 4.re.fullmatch4.1 示例1:4.2 示例2: 5.re.split5.1 示例1:5.2 示例2:5.3 示例3: 6.re.sub6.1 示例&#…...
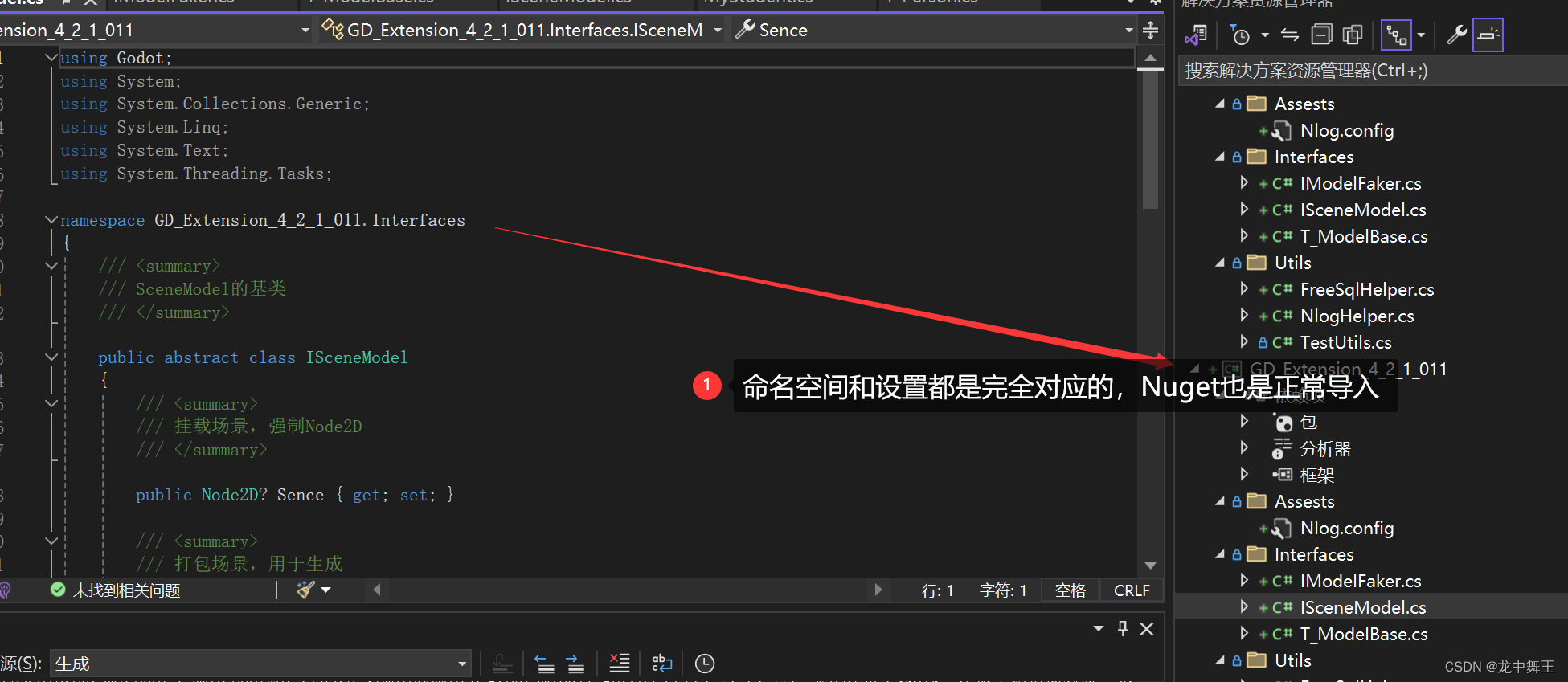
Godot.NET C# 工程化开发(1):通用Nuget 导入+ 模板文件导出,包含随机数生成,日志管理,数据库连接等功能
文章目录 前言Github项目地址,包含模板文件后期思考补充项目设置编写失误环境visual studio 配置详细的配置看我这篇文章 Nuget 推荐NewtonSoft 成功Bogus 成功Github文档地址随机生成构造器生成构造器接口(推荐) 文件夹设置Nlog 成功!Nlog.configNlogHe…...

数据仓库——雪花模式以及层次递归
层次结构 钻取 向下钻取:对某些代表事实的报表中添加维度细节 向上钻取:从某些代表事实的报表中去除维度细节 属性层次 提供了一种自然方法,用于顺序地在不断深入的层次上组织事实。许多维度可以被理解为包含连续主从关系的属性层次。此类…...
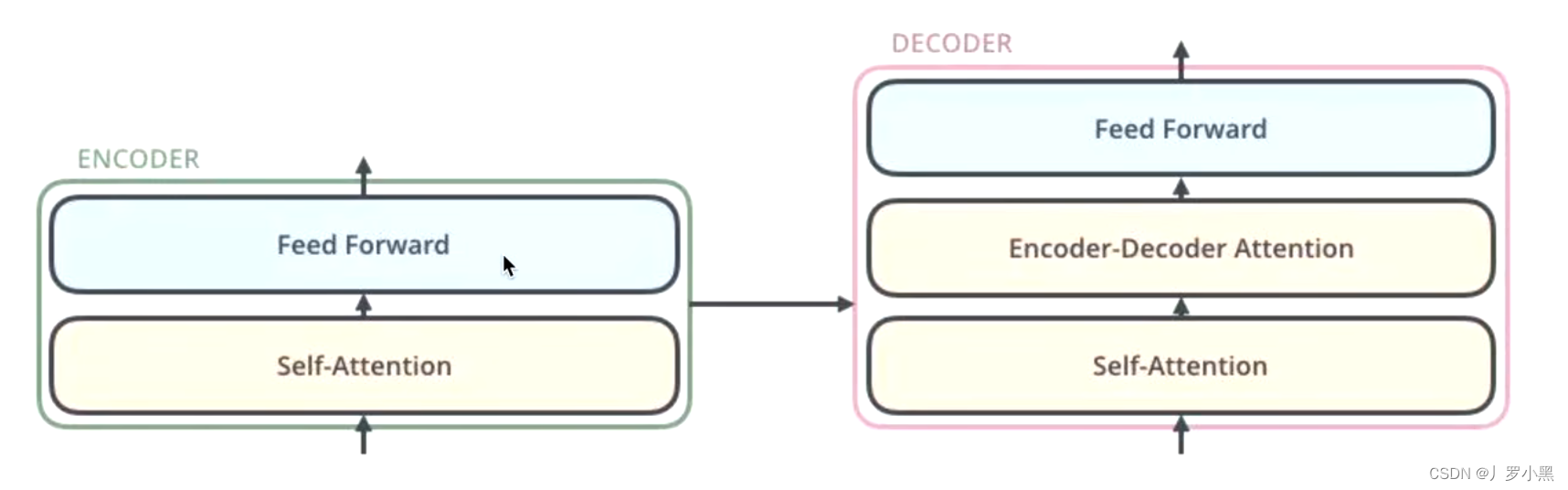
Transformer的前世今生 day09(Transformer的框架概述)
前情提要 编码器-解码器结构 如果将一个模型分为两块:编码器和解码器那么编码器-解码器结构为:编码器负责处理输入,解码器负责生成输出流程:我们先将输入送入编码器层,得到一个中间状态state,并送入解码器…...
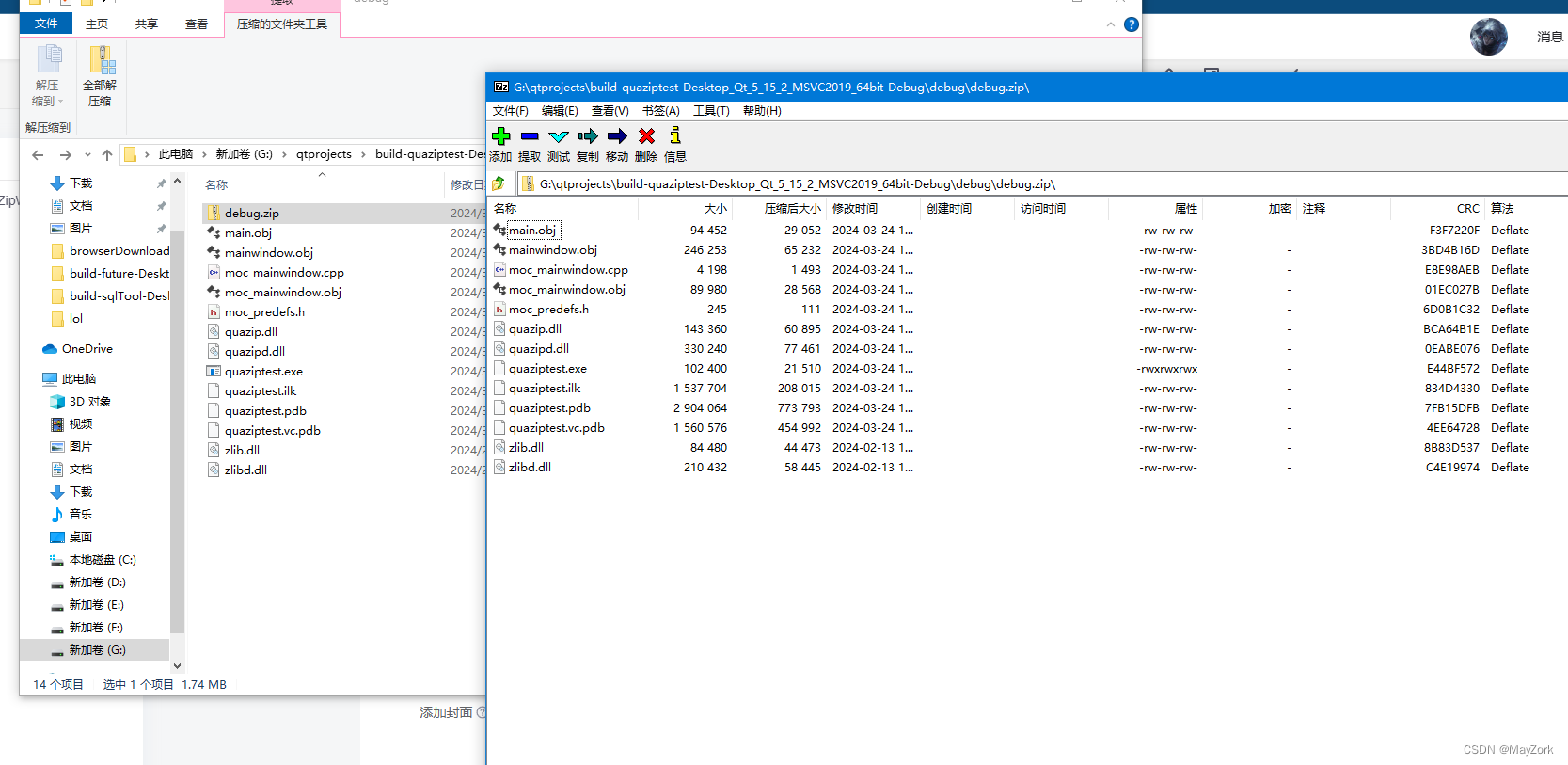
Qt 压缩/解压文件
前面讲了很多Qt的文件操作,文件操作自然就包括压缩与解压缩文件了,正好最近项目里要用到压缩以及解压缩文件,所以就研究了一下Qt如何压缩与解压缩文件。 QZipReader/QZipWriter QZipReader 和 QZipWriter 类提供了用于读取和写入 ZIP 格式文…...
——位运算+数学+一维动态规划+多维动态规划)
【leetcode刷题之路】面试经典150题(8)——位运算+数学+一维动态规划+多维动态规划
文章目录 20 位运算20.1 【位运算】二进制求和20.2 【位运算】颠倒二进制位20.3 【位运算】位1的个数20.4 【位运算】只出现一次的数字20.5 【哈希表】【位运算】只出现一次的数字 II20.6 【位运算】数字范围按位与 21 数学21.1 【双指针】回文数21.2 【数学】加一21.3 【数学】…...
JetBrains全家桶激活,分享 WebStorm 2024 激活的方案
大家好,欢迎来到金榜探云手! WebStorm公司简介 JetBrains 是一家专注于开发工具的软件公司,总部位于捷克。他们以提供强大的集成开发环境(IDE)而闻名,如 IntelliJ IDEA、PyCharm、和 WebStorm等。这些工具…...
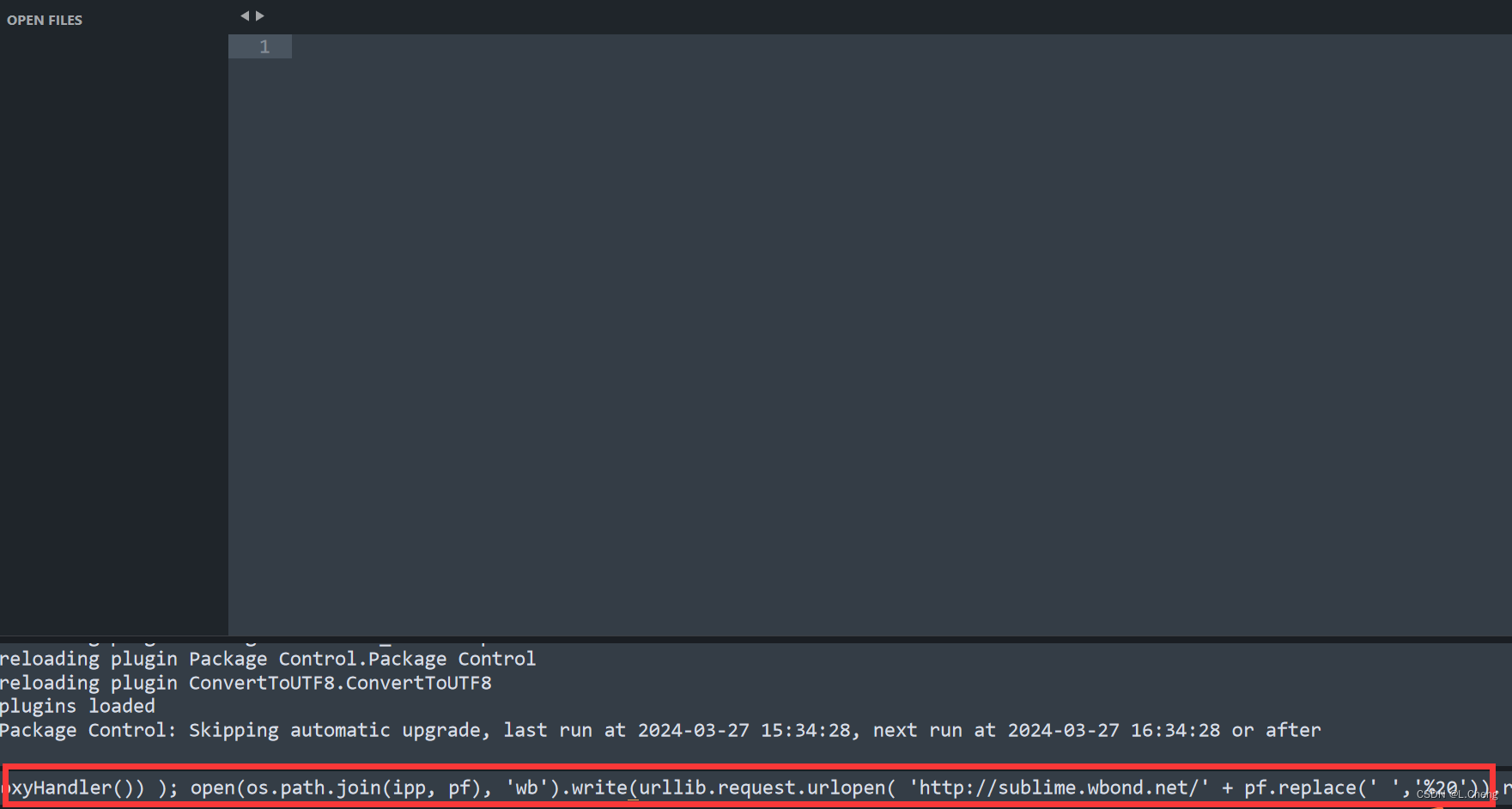
Sublime 彻底解决中文乱码
1. 按ctrl,打开Console,输入如下代码: import urllib.request,os; pf Package Control.sublime-package; ipp sublime.installed_packages_path(); urllib.request.install_opener( urllib.request.build_opener( urllib.request.ProxyHand…...

复旦大学EMBA校友出席两会建言献策助力中国发展
阳春三月,备受瞩目的全国两会如期召开。期间,复旦大学EMBA多位校友作为第十四届全国人民代表大会代表、第十四届全国政协委员与全国各地代表共商国是。 无论是作为大型央企负责人,还是作为科创企业的中坚力量,复旦大学EM…...
virtualbox导入vdi
新建虚拟机 点击新建 输入新建属性 配置cpu和内存 虚拟硬盘 这里选择已有的vdi文件 摘要 这里点击完成 虚拟机添加成功 点击启动,启动虚拟机 注意 这个时候的ip,还是以前镜像的ip,如果两个镜像一起启动,则需要修 改ip地…...

【信号处理】基于DGGAN的单通道脑电信号增强和情绪检测(tensorflow)
关于 情绪检测,是脑科学研究中的一个常见和热门的方向。在进行情绪检测的分类中,真实数据不足,经常导致情绪检测模型的性能不佳。因此,对数据进行增强,成为了一个提升下游任务的重要的手段。本项目通过DCGAN模型实现脑…...

使用 Docker Compose 部署 Spring Boot 应用
使用 Docker Compose 部署 Spring Boot 应用 第一步:创建 Spring Boot 应用的 Dockerfile 在您的 Spring Boot 项目根目录中创建一个 Dockerfile。 编辑 Dockerfile,添加以下内容: # 基础镜像使用 OpenJDK FROM openjdk:11-jdk-slim# 维护者…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
