【ONE·基础算法 || 分治·快排并归】

总言
主要内容:编程题举例,理解分治的思想(主要是对快排、并归的应用)。
文章目录
- 总言
- 1、基本介绍
- 2、颜色分类(medium)
- 2.1、题解
- 3、快速排序(medium)
- 3.1、题解:三指针版本的快排
- 4、快速选择算法(medium)
- 4.1、题解
- 5、最小的 k 个数(medium)
- 5.1、题解
- 6、归并排序(medium)
- 6.1、题解:复习快排(二路归并)
- 7、数组中的逆序对(hard)
- 7.1、题解
- 8、计算右侧小于当前元素的个数(hard)
- 8.1、题解
- 9、翻转对(hard)
- 9.1、题解
- Fin、共勉。
1、基本介绍
分治是一种解决问题的策略,它将一个大问题分解成若干个小问题,这些小问题与原问题类型相同但规模更小,然后递归地解决这些小问题,最后将小问题的解合并,从而得到原问题的解。这种策略在许多算法中都有应用,如排序、搜索、图论问题等。
快速排序就是基于分治策略的一种排序算法。它的基本思想是选取一个基准值,通过一趟排序将待排序的数据分割成独立的两部分,其中一部分的所有数据都比另一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。快速排序的时间复杂度为O(nlogn),是目前基于比较的内部排序里被认为是最好的方法,特别适用于大数据集。
归并排序则是另一种基于分治策略的排序算法。它的主要思路是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的,然后再把有序子序列合并为整体有序序列。归并排序的过程可以分为分解和合并两个步骤,分解是将序列每次折半划分,合并则是将划分后的序列段两两合并后排序。这种排序算法是稳定的,适用于各种规模的数据集。
2、颜色分类(medium)
题源:链接

2.1、题解
1)、思路分析
此题的思路本质可划分为双指针(双指针复习链接:移动零。),但对此进行了一点变动,使用的是三指针:一个用于遍历数组的指针+两个用于划分区域的指针。

PS:上述指针如何取名完全可随意,不必生搬硬套。
如何判断移动?
1、初始时: i = 0,left = -1, right = numsSize(若数组尾元素下标为n-1,right指向尾元素下一个位置,即n)
2、i从左到右遍历过程中:
①、若nums[cur] == 0 ;说明 i 位置指向的元素要纳入左区域范围内。因此,交换 left + 1 与 i 位置的元素,并让 left++ (因为纳入了新元素, 0 序列的右边界应当右滑扩展),cur++ (为什么可以 ++ ?因为 left + 1 位置要么是 0 ,要么是 1,交换完毕之后,这个位置的值已经符合我们的要求,因此 cur++ );
②、nums[cur] == 1 ;说明这个位置应该在 left 和 cur 之间,此时⽆需交换,直接让 cur++ ,判断下⼀个元素即可;
③、nums[cur] == 2 ;说明这个位置的元素应该在 right - 1 的位置,因此交换 right - 1 与 cur 位置的元素,并且让 right-- (指向 2 序列的左边界),cur 不变(因为交换过来的数是没有被判断过的,因此需要在下轮循环中判断)
2)、题解
class Solution {
public:void sortColors(vector<int>& nums) {int left = -1, right = nums.size(), i = 0;while(i < right)//right表⽰的是2序列的左边界,因此当碰到right时,说明已经将所有数据扫描完毕了{if(nums[i] == 0)swap(nums[i++],nums[++left]);else if(nums[i] == 1)i++;else //nums[i] == 2swap(nums[i],nums[--right]);//cur 不变,因为交换过来的数是没有被判断过的}}
};
3、快速排序(medium)
题源:链接

3.1、题解:三指针版本的快排
1)、思路分析
这题的题解方法有多种,这里我们主要学习快排,后续讲以同样的题讲解归并。
快排,我们在排序章节讲解过几种写法:Hoare法、挖坑法、双指针法,并且当时对key值的优化使用的是三数取中。这里我们讲解三指针法,以及随机数法选取key值。
三指针法: 这里三指针的原理同上述颜色分类。
从待排序的数组中选择一个元素作为基准值(key),以该基准值进行排序,将数组划分为左、中 、右三部分(以升序为例)。

三指针排序的过程在上述颜色分类讲解过,这里不做赘述。
在对当前序列进行三块划分处理后,再去递归排序左边部分和右边部分即可(可以舍去大量的中间部分,减少不必要的交换操作。 在处理有大量重复元素的数组时,效率会大大提升)。

随机数法取key值: 在主函数中种一颗随机数种子, 由于我们要随机产生一个满足[left,right]区间范围内的基准元素值,因此可以将生成随机数转换成为生成当前[left,right]区间的随机下标。如何做到?
(rand() % (right -left +1 )) + left
解释:这里我们设区间大小为n,让随机数 % 上区间大小,可得 [0,n-1]范围内的随机数,加上区间的左边界,即可得到 [left, left + (n -1)] 范围内的值,即[left, right]区间范围内的值。
2)、题解
class Solution {
public:void quick(vector<int>& nums, int left, int right){if(left >= right) return; //递归结束条件//随机数法选取key值int n = right - left + 1;//当前段区间内元素总数int index = (rand() % n) + left;//获取到[left, right]区间段内的随机下标int key = nums[index];//这里不能直接用key的下标进行排序(即与nums[index]比较是错误的)。//因为快排属于交换排序,index下标位置的值会在排序过程中被交换。//三指针法进行区间排序:[left,right]int i = left, l = left - 1, r = right + 1;while(i < r){if(nums[i] < key) swap(nums[++l],nums[i++]);else if(nums[i] == key) i++;else swap(nums[--r],nums[i]);//交换过来的数是没有被判断过,此处i不能++}//对左右排序:[left, l] [l+1, r-1] [r,right]quick(nums,left,l);quick(nums,r,right);}vector<int> sortArray(vector<int>& nums) {srand(time(nullptr));// 种下⼀个随机数种⼦quick(nums,0,nums.size()-1);//使用递归法排序,这里传入[left,right]区间return nums;}
};
4、快速选择算法(medium)
题源:链接

4.1、题解
1)、思路分析
这题若使用的是选择排序,比如直接选择排序或堆排序(堆排时间复杂度为 N l o g N NlogN NlogN),也可以解决此题:
class Solution {
public:int findKthLargest(vector<int>& nums, int k) {//建堆priority_queue<int> maxHeap(nums.begin(),nums.end());//取前K-1个数while(--k)//此写法下要用前置自减{maxHeap.pop();}//取第K个数return maxHeap.top();}
};
这里我们主要学习应用快排:

2)、题解
使用升序的写法:
class Solution {
public:int qsort(vector<int>& nums, int k, int left, int right) {if (left >= right) // 递归调用return nums[left];int n = right - left + 1; // 当前区间的元素总数int id = rand() % n + left; // 获取当前区间段的随机下标int key = nums[id]; // 获取该下标上的元素值(作为key值使用)int i = left, l = left - 1, r = right + 1;while (i < r) // 排升序,找第k大。{if (nums[i] < key)swap(nums[i++], nums[++l]);else if (nums[i] == key)i++;elseswap(nums[i], nums[--r]);}// 用于判断下一轮递归区间:[left,l] [l+1,r-1] [r, right]int a = l - left + 1;int b = r - 1 - (l + 1) + 1;int c = right - r + 1;if (c >= k)return qsort(nums, k, r, right);else if (b + c >= k)return key;elsereturn qsort(nums, k - b - c, left, l);}int findKthLargest(vector<int>& nums, int k) {srand(time(nullptr)); // 种下随机种子return qsort(nums, k, 0, nums.size() - 1); // 传入的区间边界应该是闭区间[left,right]}
};
使用降序的写法:只是对当前序列的排序部分及判断下一轮递归的条件做了变动。
while (i < r) // 排降序,找第k大。{if (nums[i] < key)swap(nums[i], nums[--r]);else if (nums[i] == key)i++;elseswap(nums[i++], nums[++l]);}// 用于判断下一轮递归区间:[left,l] [l+1,r-1] [r, right]int a = l - left + 1;int b = r - 1 - (l + 1) + 1;int c = right - r + 1;if (a >= k)return qsort(nums, k, left, l);else if (a + b >= k)return key;elsereturn qsort(nums, k - b - a, r, right);
5、最小的 k 个数(medium)
题源:链接

5.1、题解
1)、思路分析
此题解法多种,可用堆的TOP-K( N l o g K NlogK NlogK)、可用排序(如快排: N l o g N NlogN NlogN)、还可以用快速选择算法(即上述题4讲解的原理。)
这里主要演示快速选择算法。

2)、题解
以升序为例: 最后我们返回时,前K个元素区间虽然没有完全有序,但已经满足了找出题目最小的K个数的要求。
class Solution {
public:void qsort(vector<int>& arr, int left, int right, int k){if(left >= right) return;int n = right - left + 1;int index = rand() % n + left;int key = arr[index];//三指针排序: [left,right],排升序int L = left - 1 , R = right + 1, i = left;while(i < R){if(arr[i] < key) swap(arr[++L], arr[i++]);else if(arr[i] == key) ++i;else swap(arr[--R], arr[i]);}//对左右区间:[left, L] [L+1, R-1] [R,right]int a = L - left + 1;int b = R-1 - (L+1) + 1;int c = right - R + 1;if(a >= k) qsort(arr, left, L, k);else if(a + b >= k) return;else qsort(arr, R, right, k-a-b);}vector<int> smallestK(vector<int>& arr, int k) {srand(time(nullptr));qsort(arr,0,arr.size()-1,k);return {arr.begin(),arr.begin()+k};}
};
6、归并排序(medium)
题源:链接

6.1、题解:复习快排(二路归并)
1)、思路分析
在上述,我们用快排解过此题,这里我们使用归并排序来解决。PS:归并排序相关复习见博文:常见排序。
这里主要是指二路归并。 总体思想不变,细节实现看个人写法:
1、分割: 将待排序的数组从中间分割成两个子数组,直到子数组的大小为1(即每个子数组只包含一个元素,自然是有序的)。
2、递归排序: 递归地对子数组进行归并排序(「左半部分排序」 + 「右半部分排序」)。
3、合并: 将两个已排序的子数组合并成一个有序的大数组。(通常借助一个辅助数组,可以是每次归并时创建临时变量,也可以用全局变量或者在堆区开辟)
2)、题解
class Solution {
public:vector<int> temp;void MergeSort(vector<int>& nums, int left, int right){if(left >= right) return;//这里使用二路归并,选择中间点将区间划分为两段:[left,mid][mid+1,right]int mid = ( right + left ) / 2;//题中给出数据不大(也可以使用防越界版本的求中间值)//先对左右区间排序MergeSort(nums,left,mid);MergeSort(nums,mid+1,right);//再合并两个有序数组(来到此处,意味着当前左右两段区间各自有序)int cur1 = left; int cur2 = mid+1;int i = 0;while(cur1 <= mid && cur2 <= right)temp[i++] = nums[cur1] < nums[cur2] ? nums[cur1++] : nums[cur2++];//处理剩余区间while(cur1 <= mid) temp[i++] = nums[cur1++];while(cur2 <= right) temp[i++] = nums[cur2++];//将排序好的元素重新返回原数组中(可借助memcpy等函数)for(int j = left; j <= right; ++j){nums[j] = temp[j - left];}}vector<int> sortArray(vector<int>& nums) {temp.resize(nums.size());//归并需要借助一个辅助数组,这里可以每次归并时定义,也可以直接搞一个全局变量(或者堆上申请)MergeSort(nums,0,nums.size()-1);return nums;}
};
题外话:
理论上也可以实现k路归并排序(k-way merge sort),其中k是大于1的整数。在k路归并排序中,待排序的数组被分割成k个更小的子数组,而不是仅仅两个。然后,这k个子数组被分别排序,并最终合并成一个完整的有序数组。
k路归并排序在某些特定场景下可能具有优势,比如当待排序的数据分布在多个不连续的内存区域时,或者当使用并行计算资源时。然而,实现k路归并排序通常比实现二路归并排序更为复杂,并且不一定总是带来性能上的提升。因此,在实际应用中,二路归并排序更为常见和流行。
7、数组中的逆序对(hard)
题源:链接

7.1、题解
1)、思路分析
直接解法: 双层循环暴力枚举,看在难度hard的份上,大概率超时。
问题一:为什么可以使用归并排序?
1、题目要求找出数组中所有逆序对,既如此,将数组一分为二,先找出左区间中的逆序对,再找出右区间的逆序对,最后选出一左一右在两区间的逆序对。效果与从左到右/从右到左线性遍历查找等同。

2、对此进行优化。在找出左区间中的逆序对后我们对其排个序,同理,在找出右区间的逆序对后也对其排序。此时,尽管左右两区间内部元素顺序发生改变,但对于在两区间中分别选取元素组成一左一右的逆序对并无影响。
3、回顾上述历程,这不就和归并的思想一样吗?当然,在选取出一左一右的逆序对后,我们要对当前整体区间也进行排序。
归并排序的过程:
• 先排序左数组;
• 再排序右数组;
• 左数组和右数组合⼆为⼀。逆序对中两个元素:
• 全部从左数组中选择逆序对
• 全部从右数组中选择逆序对
• ⼀个选左数组另⼀个选右数组,组成逆序对
问题二:如何使用归并排序?及,为什么这里使用归并会提高效率(单调性)
除了这里举例的两种(升序+固定右值找左侧;降序+固定左值找右侧),如何选取与组合看个人风格。

2)、题解
升序写法如下:
class Solution {
public:int tmp[50005]={0};int mergesort(vector<int>& record, int left, int right){if(left >= right) return 0;//取中数,分区间:[left, mid] [mid+1, right]int mid = (left+right) / 2;int sum = 0;//用于统计//左区间找逆序对+排序、右区间找逆序对+排序sum += mergesort(record,left,mid)+ mergesort(record,mid+1,right);//一左一右找逆序对+排序int cur1 = left, cur2 = mid + 1;int i = 0;while(cur1 <= mid && cur2 <= right)//排升序,找左数比右数大{if(record[cur1] <= record[cur2])tmp[i++] = record[cur1++];else//record[cur1] > record[cur2]{sum += mid - cur1 + 1;tmp[i++] = record[cur2++];}}//排序:处理剩余元素while(cur1 <= mid) tmp[i++] = record[cur1++];while(cur2 <= right) tmp[i++] = record[cur2++];//将有序数列返回原数列中for(int j = left; j <= right; ++j)record[j]=tmp[j-left];//返回return sum;}int reversePairs(vector<int>& record) {return mergesort(record,0,record.size()-1);}
};
降序写法总体不变,只需稍加改动即可:
while(cur1 <= mid && cur2 <= right)//排降序,找左数比右数大{if(record[cur1] <= record[cur2])tmp[i++] = record[cur2++];else//record[cur1] > record[cur2]{sum += right - cur2 + 1;tmp[i++] = record[cur1++];}}
8、计算右侧小于当前元素的个数(hard)
题源:链接

8.1、题解
1)、思路分析
有了上一题的铺垫,这一道题的解法与之类似,但是这一道题要求的不是求总的个数,而是要返回一个数组,记录每一个元素的右边有多少个元素比自己小。

这里存在一个问题,在归并排序的过程中,元素的下标是会跟着变化的。 当前我们查找出的顺序与需要返回的顺序不一定完全匹配。

因此,为了确保返回时数组输出的元素顺序,我们需要一个额外数组 index,将数组元素和对应的下标绑定在一起归并,也就是在归并nums中元素的时候,顺势将其下标index也转移到对应的位置上。(意味着辅助数组也需要两个,分别用于排序归并后的nums、index。)
2)、题解
这是vector<int> index、vector<int> count使用全局变量的版本。
class Solution {
public:int tmp_n[100005];//辅助数组1:归并时用于排序numsint tmp_i[100005];//辅助数组2:归并时用于排序indexvector<int> index;//记录元素对应下标vector<int> count;//用于返回输出结果void mergesort(vector<int>& nums, int left, int right){if(left>=right) return;//求中值划分区间:[left,mid] [mid+1,right]int mid = (left + right) /2;//先对左右区间进行找数+归并排序:mergesort(nums, left, mid);mergesort(nums,mid+1, right);//再对当前整段区间进行找数+排序:int cur1 = left, cur2 = mid+1;int i = 0;while(cur1<=mid && cur2 <= right){if(nums[cur1] <= nums[cur2]){tmp_n[i] = nums[cur2];tmp_i[i++] = index[cur2++];//注意这里一次处理两个数组}else//nums[cur1] > nums[cur2]{count[index[cur1]] += right - cur2 + 1;tmp_n[i] = nums[cur1];tmp_i[i++] = index[cur1++];}}//处理剩余区间while(cur1 <= mid){tmp_n[i]=nums[cur1];tmp_i[i++]=index[cur1++];}while(cur2 <= right){tmp_n[i]=nums[cur2];tmp_i[i++]=index[cur2++];}//将获取到的有序数据写回原数组中for(int j = left; j <= right; ++j){nums[j]=tmp_n[j-left];index[j]=tmp_i[j-left];}}vector<int> countSmaller(vector<int>& nums) {int n = nums.size();index.resize(n);//重新扩容count.resize(n);for(int i = 0; i < n; ++i)//初始化下标{index[i] = i;}mergesort(nums, 0, n-1);return count;}
};
如果不使用全局变量,也可如下,但需要传参时多增几个参数。总之写法不一。
class Solution {
public:int tmp_n[100005];int tmp_i[100005];void mergesort(vector<int>& nums, int left, int right, vector<int>& index, vector<int>& count){if(left >= right) return;//[left,mid] [mid+1,right]int mid = (left + right) /2;//左右区间:mergesort(nums, left, mid, index,count);mergesort(nums,mid+1, right, index,count);//当前整个区间:int cur1 = left, cur2 = mid+1;int i = 0;while(cur1<=mid && cur2 <= right){if(nums[cur1] <= nums[cur2]){tmp_n[i] = nums[cur2];tmp_i[i++] = index[cur2++];}else//nums[cur1] > nums[cur2]{count[index[cur1]] += right - cur2 + 1;tmp_n[i] = nums[cur1];tmp_i[i++] = index[cur1++];}}//处理剩余区间while(cur1 <= mid){tmp_n[i]=nums[cur1];tmp_i[i++]=index[cur1++];}while(cur2 <= right){tmp_n[i]=nums[cur2];tmp_i[i++]=index[cur2++];}//写回原数组中for(int j = left; j <= right; ++j){nums[j]=tmp_n[j-left];index[j]=tmp_i[j-left];}}vector<int> countSmaller(vector<int>& nums) {int n = nums.size();vector<int> index(n);vector<int> count(n);for(int i = 0; i < n; ++i){index[i] = i;}mergesort(nums, 0, n-1, index, count);return count;}
};
关于count[index[cur1]] += right - cur2 + 1; 为什么要用+=,而不能使用+?
要知道归并的过程,元素位置是变化的。 使用 += 是因为我们需要累计 nums[cur1] 右侧小于它的元素数量。在归并排序的合并过程中,cur1 会遍历左子数组的所有元素,每次遇到一个比右子数组当前元素大的左子数组元素时,我们都需要将右子数组中剩余的元素数量(即 right - cur2 + 1)累加到对应的 count 中。因此,这是一个累加操作,每次都需要将新的数量加到之前累计的数量上。
如果使用 + 而不是 +=,那么每次只会将 right - cur2 + 1 赋值给 count[index[cur1]],而不会保留之前累计的数量。这会导致 count 数组中每个位置只存储了最后一次计算得到的数量,而不是所有累计的数量,从而得到错误的结果。

9、翻转对(hard)
题源:链接

9.1、题解
1)、思路分析
翻转对和逆序对的定义大同小异,逆序对是前面的数要大于后面的数。而翻转对是前面的一个数要大于后面某个数的两倍。因此,我们依旧可以用归并排序的思想来解决这个问题。
而与上个问题不同的是,上一道题我们可以一边合并一遍计算小于当前元素右侧元素,但是这道题要求的是左边元素大于右边元素的两倍,若直接合并的话,是无法快速计算出翻转对的数量的。
因此,在归并排序之前,我们可以借助左右区间已经排序好的单调性,先完成对翻转对的统计。由于两个指针都是不回退的的扫描到数组的结尾,因此两个有序序列求出翻转对的时间复杂度是 O ( N ) O(N) O(N)。

2)、题解
以升序为例:
class Solution {
public:int tmp[50005] = {0};int mergesort(vector<int>& nums, int left, int right) {if (left >= right)return 0;//[left,mid] [mid+1, right]int mid = (left + right) / 2;int sum = 0;sum += mergesort(nums, left, mid) + mergesort(nums, mid + 1, right);// 统计:(单调性为升序)int cur1 = left, cur2 = mid + 1;while(cur1 <= mid && cur2 <= right){if(nums[cur1]/2.0 > nums[cur2]){sum += mid - cur1 + 1;cur2++;}else cur1++;}// while (cur2 <= right) // 统计部分其它写法:升序的情况// {// while (cur1 <= mid && nums[cur2] >= nums[cur1] / 2.0)// cur1++;// if (cur1 > mid)// break;// sum += mid - cur1 + 1;// cur2++;// }// 排序:升序版,[left, mid][mid+1, right]cur1 = left, cur2 = mid + 1;int i = left;while (cur1 <= mid && cur2 <= right) {if (nums[cur1] > nums[cur2])tmp[i++] = nums[cur2++];elsetmp[i++] = nums[cur1++];}while (cur1 <= mid)tmp[i++] = nums[cur1++];while (cur2 <= right)tmp[i++] = nums[cur2++];//写回for (int j = left; j <= right; ++j) {nums[j] = tmp[j];}return sum;}int reversePairs(vector<int>& nums) {return mergesort(nums, 0, nums.size()-1);}
};
以降序为例:
class Solution {
public:int tmp[50005] = {0};int mergesort(vector<int>& nums, int left, int right) {if (left >= right)return 0;//[left,mid] [mid+1, right]int mid = (left + right) / 2;int sum = 0;sum += mergesort(nums, left, mid) + mergesort(nums, mid + 1, right);// 统计:(单调性为降序)int cur1 = left, cur2 = mid + 1;while (cur1 <= mid && cur2 <= right) {if (nums[cur1] / 2.0 > nums[cur2]) {sum += right - cur2 + 1;cur1++;} elsecur2++;}// while (cur1 <= mid) // 统计部分其它写法:降序的情况// {// while (cur2 <= right && nums[cur2] >= nums[cur1] / 2.0)// cur2++;// if (cur2 > right)// break;// ret += right - cur2 + 1;// cur1++;// }// 排序:降序版,[left, mid][mid+1, right]cur1 = left, cur2 = mid + 1;int i = left;while (cur1 <= mid && cur2 <= right) {tmp[i++] = nums[cur1] > nums[cur2] ? nums[cur1++] : nums[cur2++];}while (cur1 <= mid)tmp[i++] = nums[cur1++];while (cur2 <= right)tmp[i++] = nums[cur2++];// 写回for (int j = left; j <= right; ++j) {nums[j] = tmp[j];}return sum;}int reversePairs(vector<int>& nums) {return mergesort(nums, 0, nums.size() - 1);}
};
Fin、共勉。

相关文章:

【ONE·基础算法 || 分治·快排并归】
总言 主要内容:编程题举例,理解分治的思想(主要是对快排、并归的应用)。 文章目录 总言1、基本介绍2、颜色分类(medium)2.1、题解 3、快速排序(medium)3.1、题解ÿ…...
注册新用户)
Python 从0开始 一步步基于Django创建项目(11)注册新用户
1、修改C:\D\Python\Python310\study\snap_gram\users路径下的urls.py 添加‘注册新用户’URL。 #注册新用户 path(register/,views.register,nameregister), 2、修改C:\D\Python\Python310\study\snap_gram\users路径下的views.py 编写URL对应的视图函数register。 def r…...

银行监管报送系统介绍(十二):非居民金融账户涉税信息报送
国家税务总局、财政部、中国人民银行、中国银行业监督管理委员会、中国证券监督管理委员会、国家金融监督管理总局2017年5月9日发布、2017年7月1日起施行的《非居民金融账户涉税信息尽职调查管理办法》。 一、《管理办法》出台的背景是什么? 受二十国集团&…...
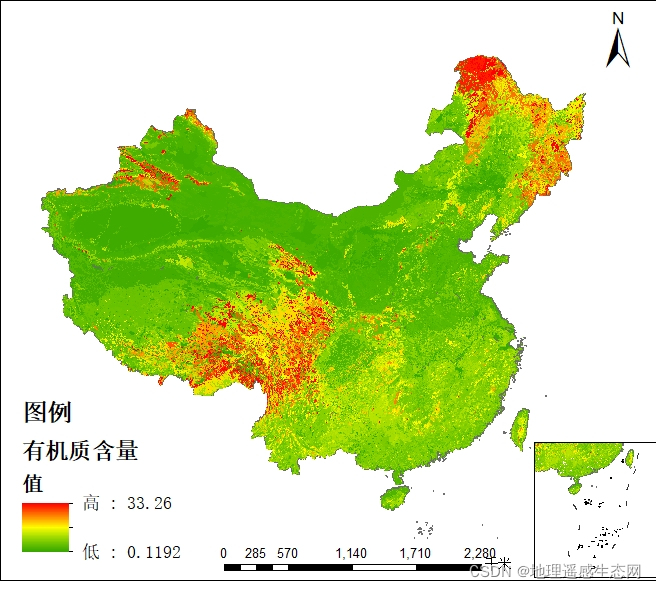
土壤有机质空间分布数据
土壤有机质(soil organic matter)是土壤中含碳有机化合物的总称,包括土壤固有的和外部加入的所有动植物残体及其分解产物和合成产物。主要来源于动植物及微生物残体,可分为腐殖质和非腐殖物质。一般占土壤固相总重的10%以下&#…...
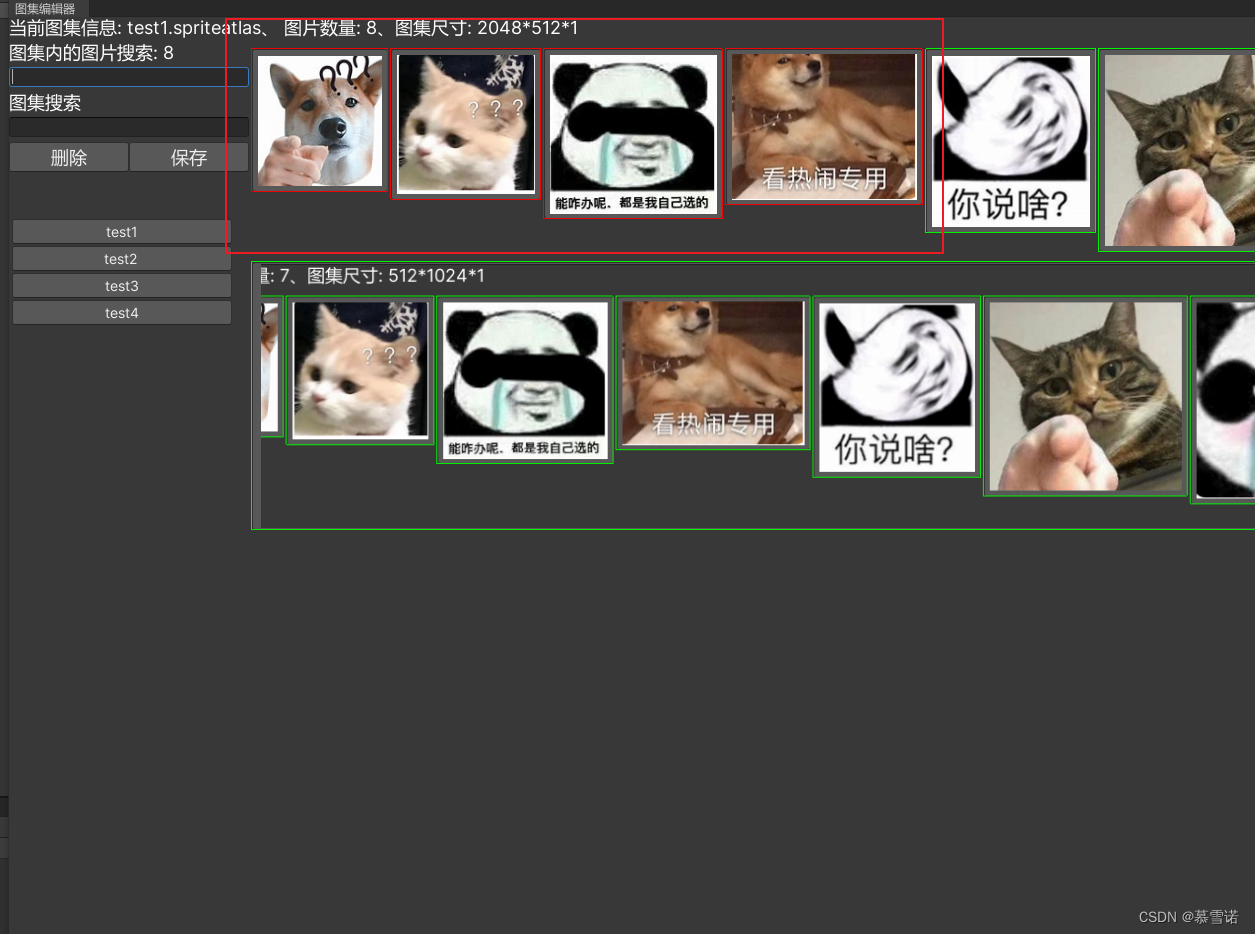
Unity图集编辑器
图集编辑器 欢迎使用图集编辑器新的改变编辑器图片 欢迎使用图集编辑器 Unity图集操作很是费劲 无法批量删除和添加图集中的图片 新的改变 自己写了一个图集编辑器 客: 支持批量删除 左键点击图片代表选中 右键点击图标定位到资产支持批量添加 选中图片拖拽到编…...
)
【JS笔记】JavaScript语法 《基础+重点》 知识内容,快速上手(六)
面向对象OOP 首先,我们要明确,面向对象不是语法,是一个思想,是一种 编程模式面向: 面(脸),向(朝着)面向过程: 脸朝着过程 》 关注着过程的编程模…...
hbase启动错误-local host is“master:XXXX“ destination is:master
博主的安装前提: zookeeper安装完成,且启动成功 hdfs高可用安装,yarn高可用安装,且启动成功 报错原因:端口配置不对 解决方案: 输入:hdfs getconf -confKey fs.default.name 然后把相应的…...
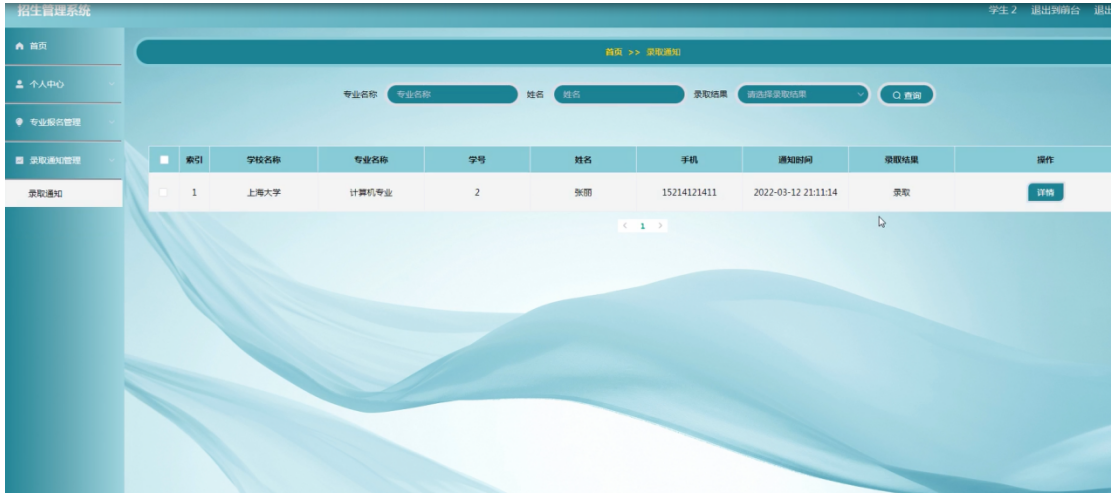
基于SpringBoot的“招生管理系统”的设计与实现(源码+数据库+文档+PPT)
基于SpringBoot的“招生管理系统”的设计与实现(源码数据库文档PPT) 开发语言:Java 数据库:MySQL 技术:SpringBoot 工具:IDEA/Ecilpse、Navicat、Maven 系统展示 系统功能结构图 系统首页界面图 学生注册界面图 …...

Chinese-LLaMA-Alpaca-2模型量化部署测试
简介 Chinese-LLaMA-Alpaca-2基于Meta发布的可商用大模型Llama-2开发, 是中文LLaMA&Alpaca大模型的第二期项目. 量化 模型的下载还是应用脚本 bash hfd.sh hfl/chinese-alpaca-2-13b --tool aria2c -x 8应用llama.cpp进行量化, 主要参考该教程. 其中比较折腾的是与BLAS…...

flutter 打包成web应用后怎么通过url跳转页面
在 Flutter 中,如果你想要在打包成 Web 应用后通过 URL 跳转页面,你可以利用 Flutter 提供的路由导航系统和 URL 策略。以下是具体步骤: 1. 配置路由 在 Flutter 应用中定义路由,一种简单的方式是使用 MaterialApp 构造器的 rou…...
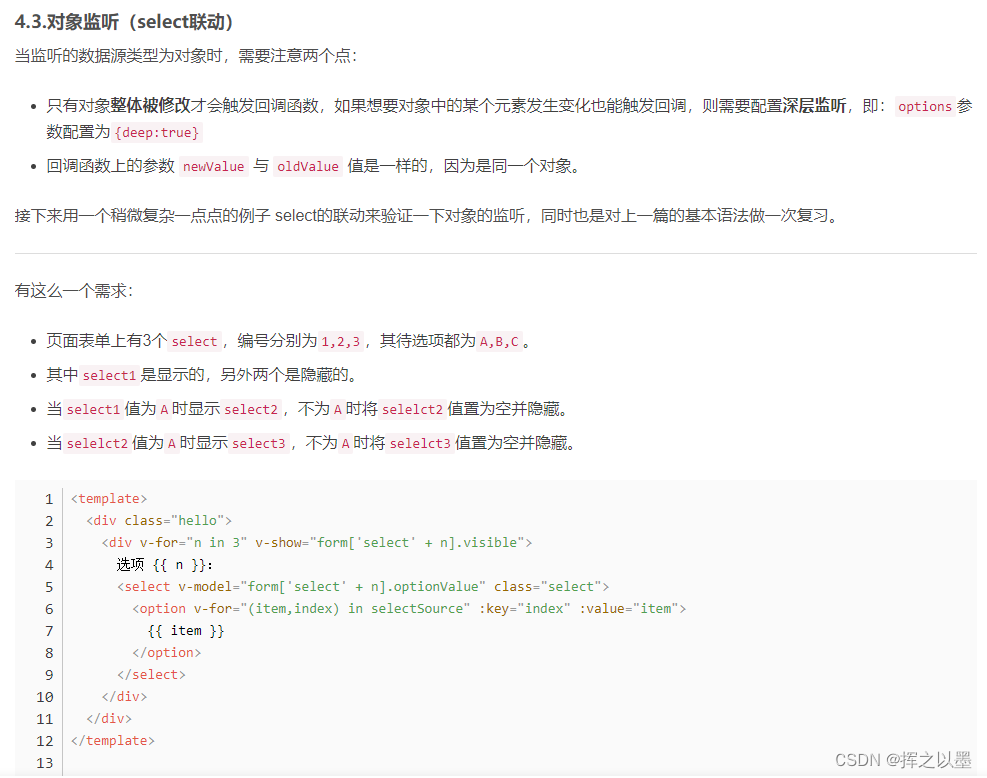
【设计模式】中介者模式的应用
文章目录 1.概述2.中介者模式的适用场景2.1.用户界面事件2.2.分布式架构多模块通信 3.总结 1.概述 中介者模式(Mediator Pattern)是一种行为型设计模式,它用于解决对象间复杂、过度耦合的问题。当多个对象(一般是两个以上的对象&…...

【微服务篇】分布式事务方案以及原理详解
分布式事务是指事务参与者、资源服务器、事务管理器分布在不同的分布式系统的多个节点之上的事务。在微服务架构、大型分布式系统和云计算等环境中,由于系统间调用和资源访问的复杂性,分布式事务变得尤为重要。 应用场景 跨系统交易:当交易…...

String 类的常用方法都有那些?
String 类在 Java 中是一个非常重要的类,用于处理文本数据。它提供了许多方法来操作字符串。以下是一些 String 类的常用方法: 构造方法 String(): 创建一个新的空字符串对象。String(byte[] bytes): 使用指定的字节数组来创建一个新的 String 对象。S…...

用XMLHttpRequest发送和接收JSON数据
百度的AI回答了一个案例: var xhr new XMLHttpRequest(); var url "your_endpoint_url"; // 替换为你的API端点 var data JSON.stringify({key1: "value1",key2: "value2" });xhr.open("POST", url, true); xhr.setReq…...
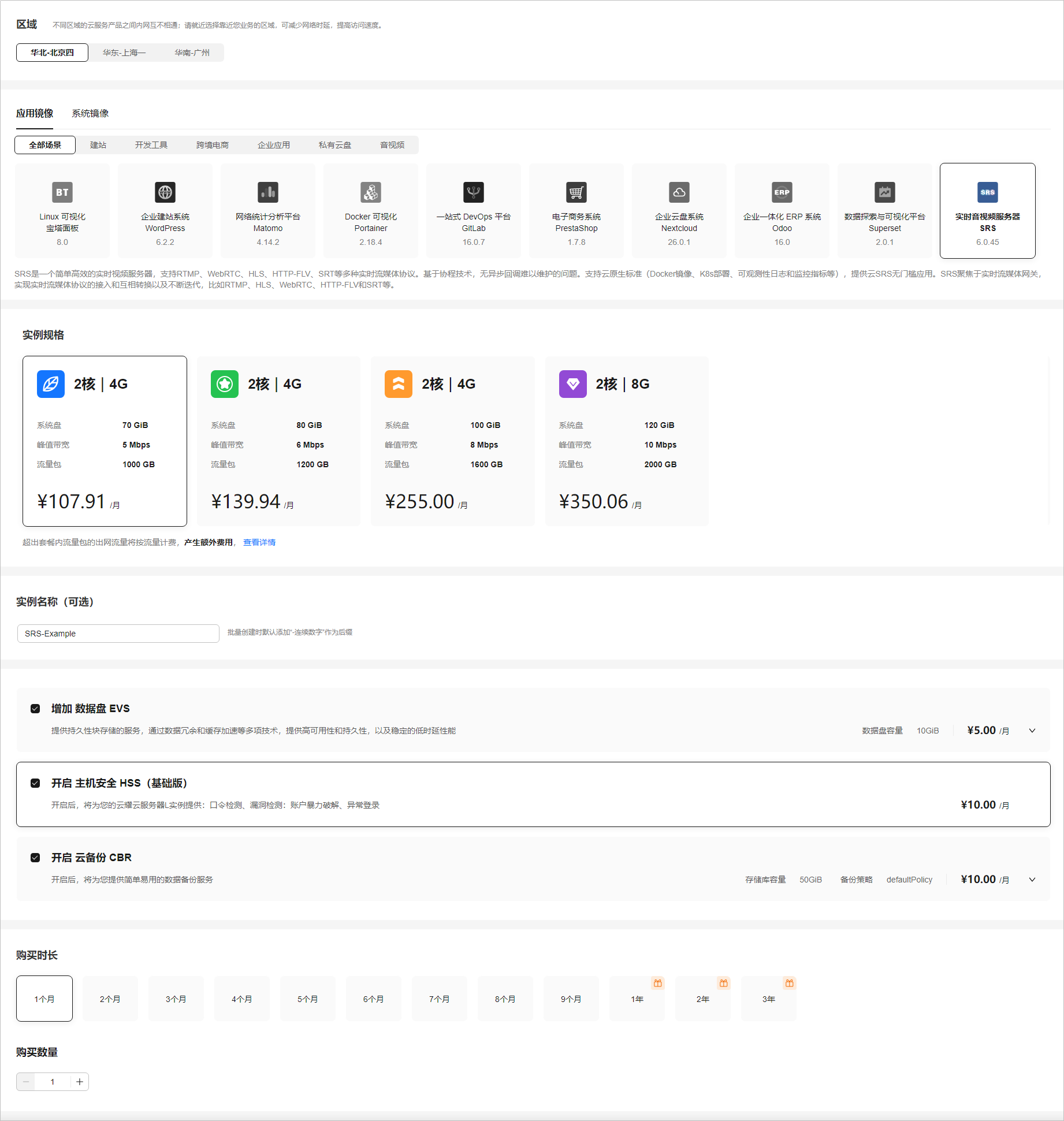
华为云使用指南02
5.使用GitLab进行团队及项目管理 GitLab旨在帮助团队进行项目开发协作,为软件开发和运营生命周期提供了一个完整的DevOps方案。GitLab功能包括:项目源码的管理、计划、创建、验证、集成、发布、配置、监视和保护应用程序等。该镜像基于CentOS操…...

halcon目标检测标注保存
* 创建一个新的字典 create_dict(ObjectDictionary) * 类别名称列表和对应的ID列表 class_names : [Defect1,Defect2,Defect3,Defect4,Defect5,Defect6,Defect7,Defect8,Defect9,Defect10,Defect11,Defect12,Defect13,Defect14,Defect15,Defect16,Defect17,Defect18] class_id…...
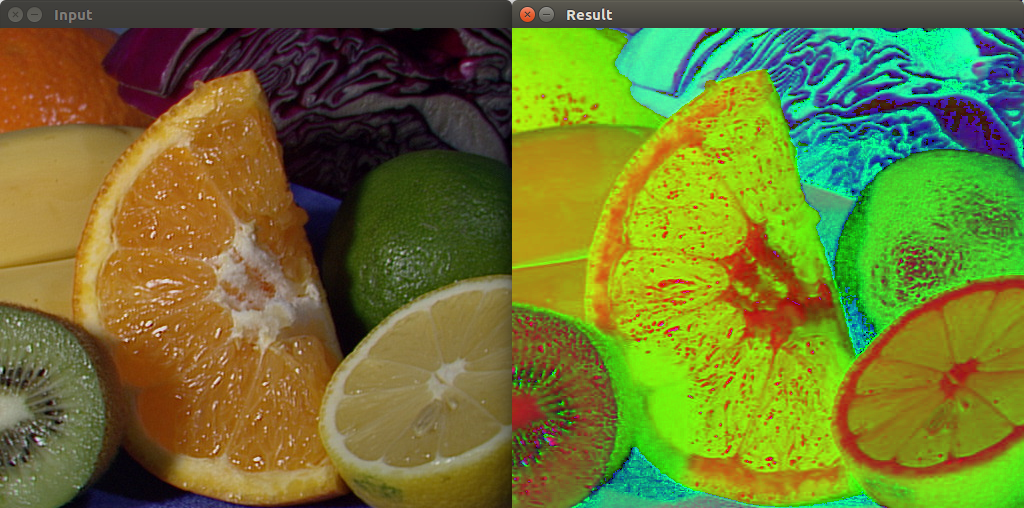
Python图像处理——计算机视觉中常用的图像预处理
概述 在计算机视觉项目中,使用样本时经常会遇到图像样本不统一的问题,比如图像质量,并非所有的图像都具有相同的质量水平。在开始训练模型或运行算法之前,通常需要对图像进行预处理,以确保获得最佳的结果。图像预处理…...

编译安装飞桨fastdeploy@FreeBSD(失败)
FastDeploy是一款全场景、易用灵活、极致高效的AI推理部署工具, 支持云边端部署。提供超过 🔥160 Text,Vision, Speech和跨模态模型📦开箱即用的部署体验,并实现🔚端到端的推理性能优化。包括 物…...
)
java组合总和(力扣Leetcode39)
组合总和 力扣原题链接 问题描述 给定一个无重复元素的整数数组 candidates 和一个目标整数 target,找出 candidates 中可以使数字和为目标数 target 的所有不同组合,并以列表形式返回。你可以按任意顺序返回这些组合。 示例 示例 1: 输…...

ZK友好代数哈希函数安全倡议
1. 引言 前序博客: ZKP中的哈希函数如何选择ZK-friendly 哈希函数?snark/stark-friendly hash函数Anemoi Permutation和Jive Compression模式:高效的ZK友好的哈希函数Tip5:针对Recursive STARK的哈希函数 随着Incrementally Ve…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...

GeoServer发布PostgreSQL图层后WFS查询无主键字段
在使用 GeoServer(版本 2.22.2) 发布 PostgreSQL(PostGIS)中的表为地图服务时,常常会遇到一个小问题: WFS 查询中,主键字段(如 id)莫名其妙地消失了! 即使你在…...

比特币:固若金汤的数字堡垒与它的四道防线
第一道防线:机密信函——无法破解的哈希加密 将每一笔比特币交易比作一封在堡垒内部传递的机密信函。 解释“哈希”(Hashing)就是一种军事级的加密术(SHA-256),能将信函内容(交易细节…...

C/Python/Go示例 | Socket Programing与RPC
Socket Programming介绍 Computer networking这个领域围绕着两台电脑或者同一台电脑内的不同进程之间的数据传输和信息交流,会涉及到许多有意思的话题,诸如怎么确保对方能收到信息,怎么应对数据丢失、被污染或者顺序混乱,怎么提高…...
