滑动窗口_水果成篮_C++

题目:
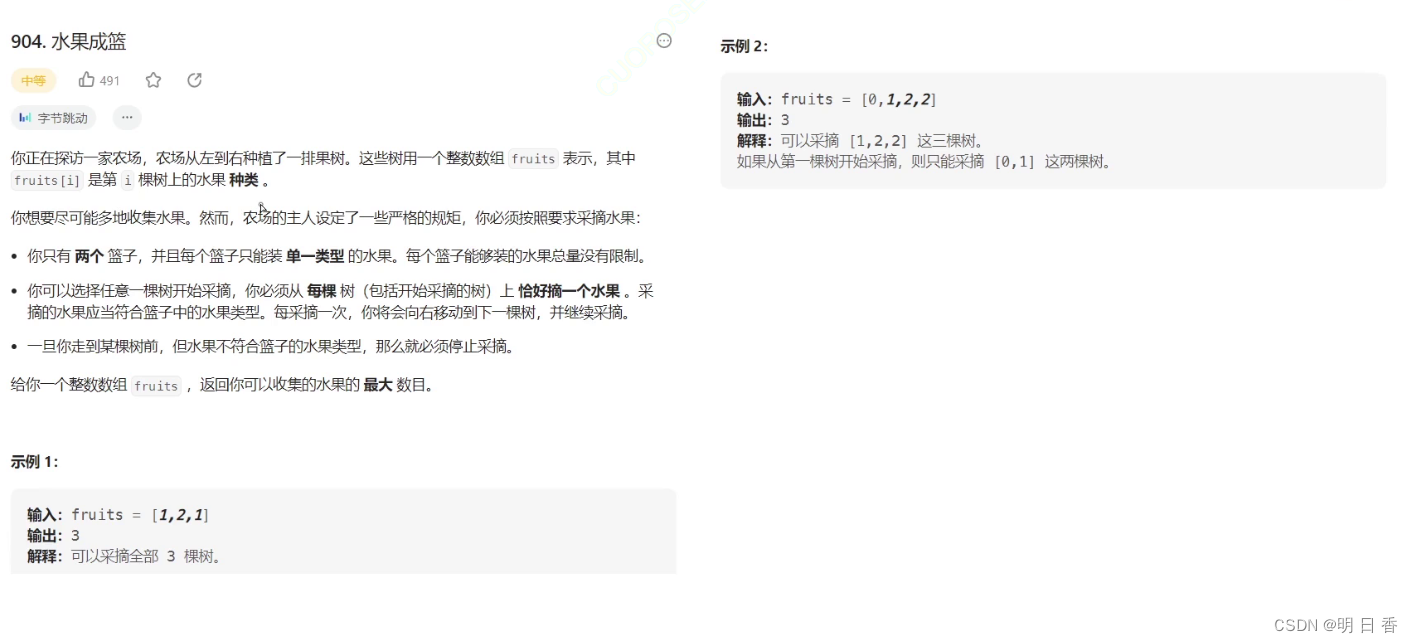
题目解析:
- fruits[i]表示第i棵树,这个fruits[i]所表示的数字是果树的种类
- 例如示例1中的[1,2,1],表示第一棵树 的种类是 1,第二个树的种类是2 第三个树的种类是1
- 随后每一个篮子只能装一种类型的水果,我们有两个篮子
- 所以最后求的是可以采摘几棵树
- 问题转化就是求最长的连续的子数组!而且这个数组只能有两种数字!
算法原理:

根据题目的解析,我们需要知道本题需要 用于计算水果种类的 kinds 、用于存储水果的果篮 hash、用于寻找连续数组的指针 right、left
使用left指针进行固定,从最左端开始,而right指针开始移动进行水果的摘取 ,同时一边摘取水果一边将水果放入篮子内部,同时更新right和left之间的距离长度,以此来获取最大的连续子数组长度。
在水果摘取的过程中,因为篮子内部只能是两种水果,所以使用数组,把代表水果的数字作为下标,进行水果的数量记载,当遇到第三个水果时,right停止移动,表示篮子内部的两种水果的组合在当前结束了。
而当right停止移动时,left就要开始移动,因为篮子只能存在两种水果,且需要子数组连续,所以可以让left一边移动的同时一边减去指向的元素的个数,使得水果的数量减少的同时也能够将果篮内的另一个水果排除,让水果篮内部至少留下一个水果,和新种类的水果组成新的组合。
当水果蓝内的水果只剩下一种时,left停止移动,而right开始重新移动,直到遇见另一个新的水果停下,之后重复之前的操作。

代码编写:
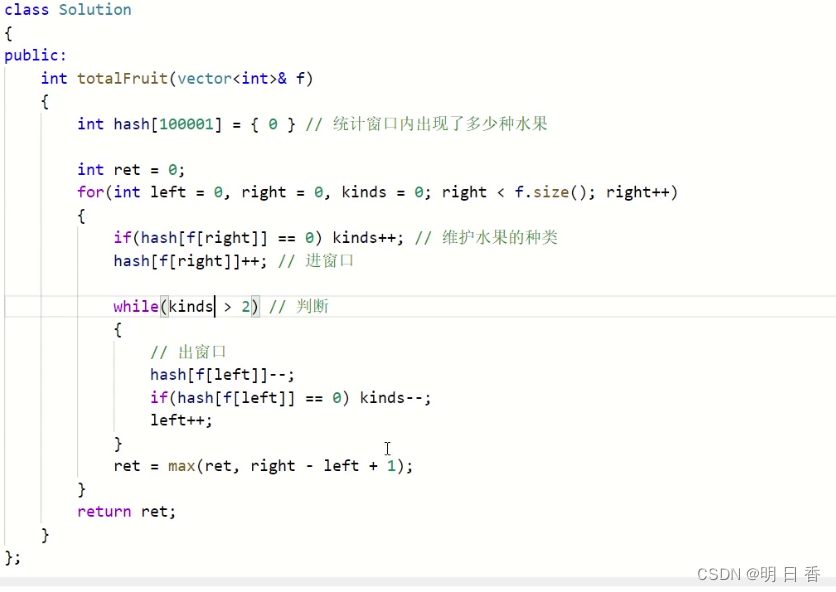
- 使用一个内容巨大的数组来充当水果篮子
- hash[f[right]]和hash[f[left]]表示的是这个元素的数量。相当于是让这个元素变成一种下标索引,在这个超级大的数组内部,进行数量的统计!
- kinds表示一共有多少种类的元素,最多只能是2
- 当kind大于2时我们需要减去left指向的元素的个数,同时因为种类的原因,且需要进行连续,所以在种类重新编程小于等于2之前,元素的个数都必须减少,直到某一个元素消失kind小于等于2为止!
相关文章:

滑动窗口_水果成篮_C++
题目: 题目解析: fruits[i]表示第i棵树,这个fruits[i]所表示的数字是果树的种类例如示例1中的[1,2,1],表示第一棵树 的种类是 1,第二个树的种类是2 第三个树的种类是1随后每一个篮子只能装一种类型的水果,我…...
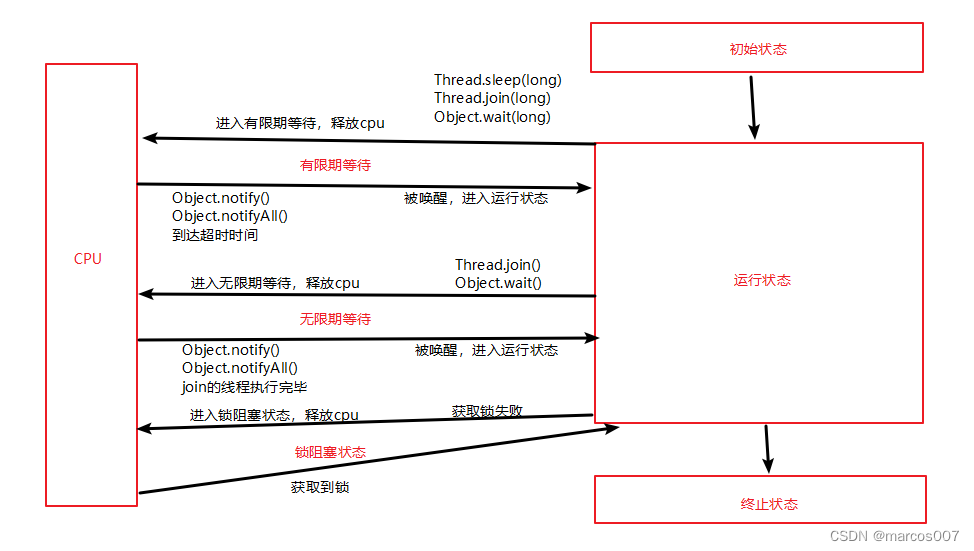
线程的状态:操作系统层面和JVM层面
在操作系统层面,线程有五种状态 初始状态:线程被创建,操作系统为其分配资源。 可运行状态(就绪状态):线程被创建完成,进入就绪队列,参与CPU执行权的争夺。或因为一些原因,从阻塞状态唤醒的线程…...

在Isaac-sim中弧度转四元数以及四元数转弧度的问题
问题: 在Isaac-sim中如果采用set_world_pose()和get_world_pose()得到的都是四元数,如何将弧度转四元数,或者将四元数转为弧度是需要解决的一个问题, 这里的弧度是以x轴为0度,y轴为90度,逆时针方向逐渐增大…...

【计算机网络】高级IO模型
高级IO模型 一、 理解 IO二、认识五种高级 IO 模型1. 阻塞 IO2. 非阻塞IO3. 信号驱动 IO4. IO 多路转接5. 异步 IO 三、高级 IO 重要概念1. 阻塞和非阻塞2. 同步通信和异步通信 四、非阻塞 IOfcntl 一、 理解 IO 当我们调用系统接口 write、read 的时候,本质是把数…...

LabVIEW电动汽车直流充电桩监控系统
LabVIEW电动汽车直流充电桩监控系统 随着电动汽车的普及,充电桩的安全运行成为重要议题。通过集成传感器监测、单片机技术与LabVIEW开发平台,设计了一套电动汽车直流充电桩监控系统,能实时监测充电桩的温度、电压和电流,并进行数…...
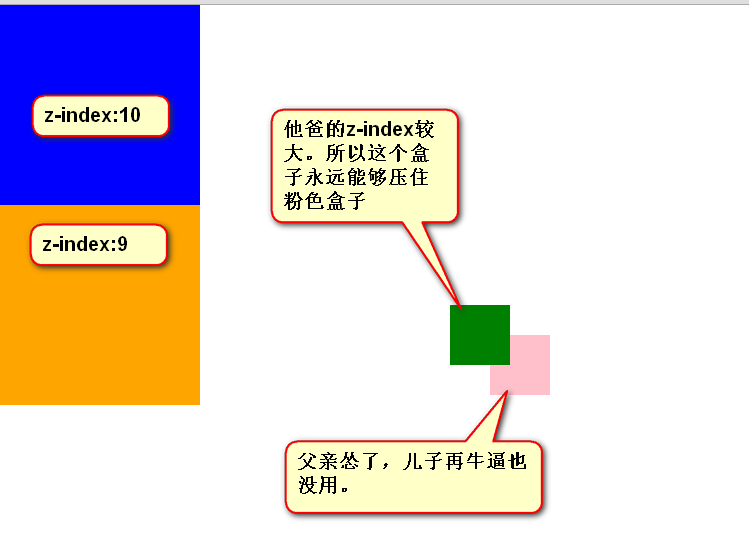
前端学习<二>CSS基础——08-CSS属性:定位属性
CSS的定位属性有三种,分别是绝对定位、相对定位、固定定位。 position: absolute; <!-- 绝对定位 -->position: relative; <!-- 相对定位 -->position: fixed; <!-- 固定定位 --> 下面逐一介绍。 相对定位 相对定位:让…...
)
88. 合并两个有序数组(javascript)
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。 注意:最终,合并后数组…...

机器学习_集成学习_梯度提升_回归_决策树_XGBoost相关概念
目录 1. 机器学习 使用监督吗?什么又是监督学习? 2. 与XGBoost 类似的机器学习方法有哪些? 3. 随机森林方法 和 梯度提升方法 有什么区别? 分别应用于什么场景? 4. 决策树回归方法 和 Gradient Boosting类回归方法…...
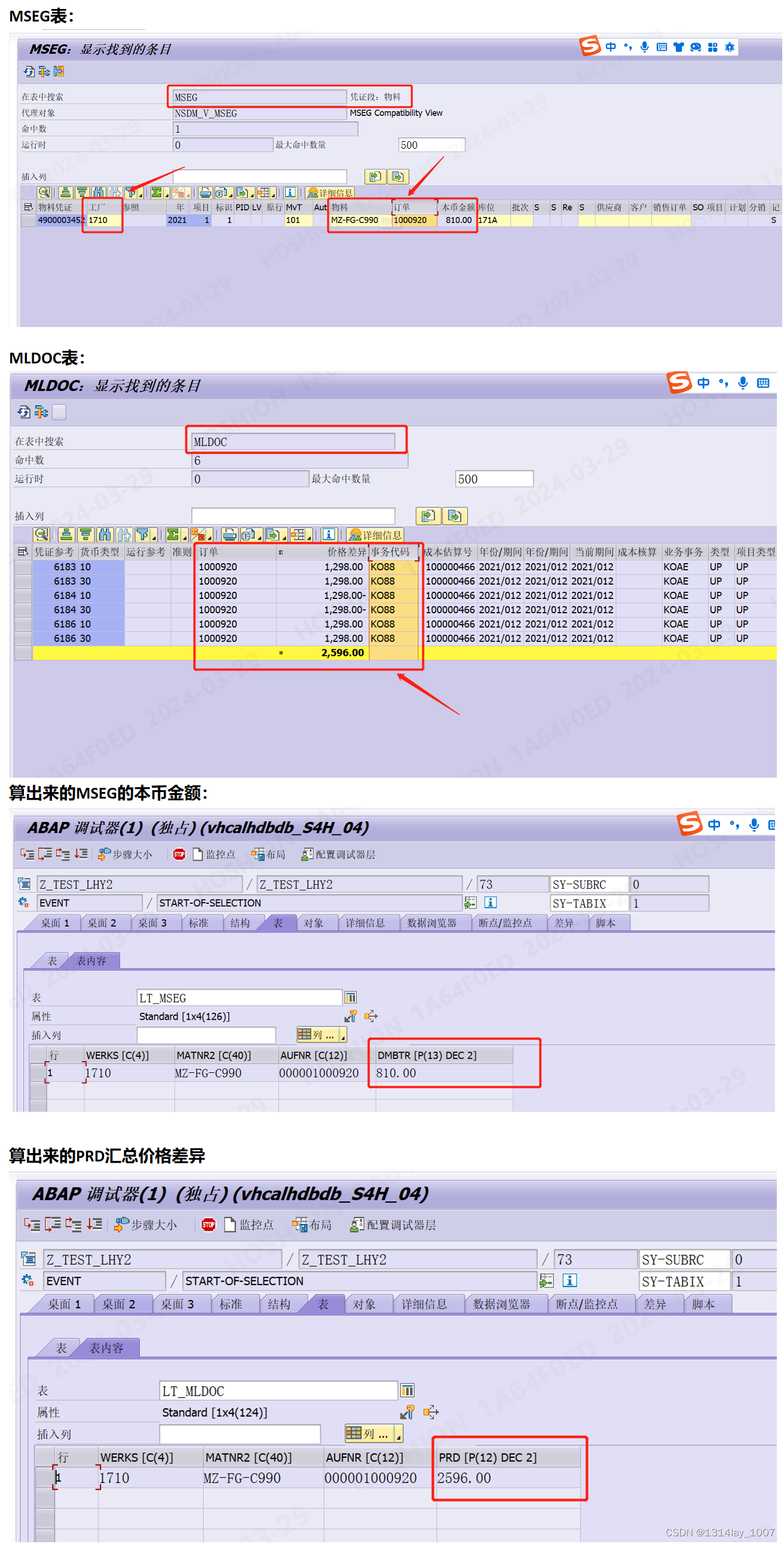
ABAP 字段类型不一样导致相加之后金额错误
文章目录 ABAP 字段类型不一样导致相加之后金额错误写在前面的总结示例程序1汇总MSEG表和MLDOC表 ABAP 字段类型不一样导致相加之后金额错误 写在前面的总结 如果需要不同底表的字段相加的值,那么最好是根据条件去分别算出那些值放在临时内表里面,再去…...

【L1距离和L2距离】Manhattan Distance Euclidean Distance 解释和计算公式
距离度量 特征空间中两个实例点的距离可以反映出两个实力点之间的相似性程度,使用的距离可以是欧式距离,也可以是其他距离。 欧氏距离(L2距离):最常见的两点之间或多点之间的距离表示法,又称之为欧几里得度量,它定义于…...
自动发卡平台源码优化版,支持个人免签支付
源码下载地址:自动发卡平台源码优化版.zip 环境要求: php 8.0 v1.2.6◂ 1.修复店铺共享连接时异常问题 2024-03-13 23:54:20 v1.2.5 1.[新增]用户界面硬币增款扣款操作 2.[新增]前台对接库存信息显示 3.[新增]文件缓存工具类[FileCache] 4.[新增]库存同…...

如何使用固定公网地址远程连接Python编译器并将运行结果返回到Pycharm
文章目录 一、前期准备1. 检查IDE版本是否支持2. 服务器需要开通SSH服务 二、Pycharm本地链接服务器测试1. 配置服务器python解释器 三、使用内网穿透实现异地链接服务器开发1. 服务器安装Cpolar2. 创建远程连接公网地址 四、使用固定TCP地址远程开发 本文主要介绍如何使用Pych…...
Java设计模式—备忘录模式(快照模式)
定义 备忘录模式提供了一种状态恢复的实现机制,使得用户可以方便地回到一个特定的历史步骤,当新的状态无效或者存在问题时,可以使用暂时存储起来的备忘录将状态复原,很多软件都提供了撤销(Undo)操作&#…...
没学数模电可以玩单片机吗?
我们首先来看一下数电模电在单片机中的应用。数电知识在单片机中主要解决各种数字信号的处理、运算,如数制转换、数据运算等。模电知识在单片机中主要解决各种模拟信号的处理问题,如采集光照强度、声音的分贝、温度等模拟信号。而数电、模电的相互转换就…...

FlinkSQL之Flink SQL Join二三事
Flink SQL支持对动态表进行复杂而灵活的连接操作。 为了处理不同的场景,需要多种查询语义,因此有几种不同类型的 Join。默认情况下,joins 的顺序是没有优化的。表的 join 顺序是在 FROM 从句指定的。可以通过把更新频率最低的表放在第一个…...

某某消消乐增加步数漏洞分析
一、漏洞简介 1) 漏洞所属游戏名及基本介绍:某某消消乐,三消游戏,类似爱消除。 2) 漏洞对应游戏版本及平台:某某消消乐Android 1.22.22。 3) 漏洞功能:增加游戏步数。 4…...
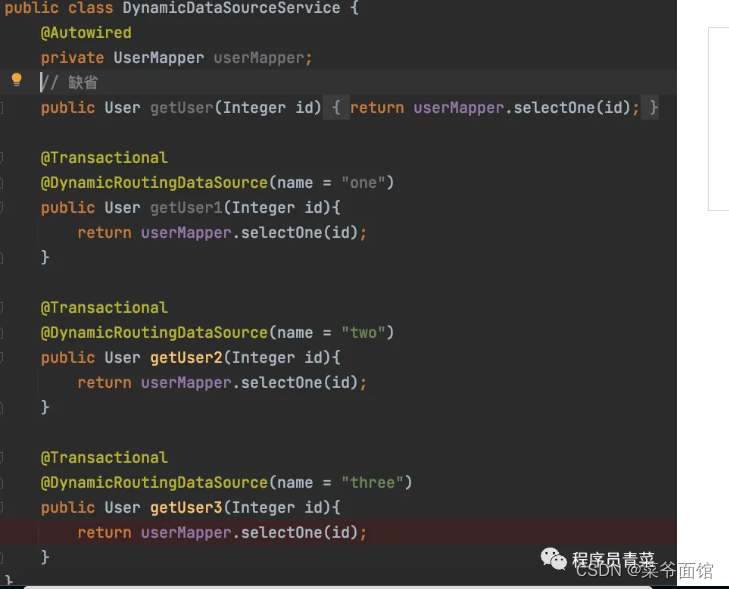
SpringBoot动态数据源实现
一、背景 一个应用难免需要连接多个数据库,像我们系统起码连接了5个以上数据库,AWS RDS主库,ECS自搭MySQL从库,工厂系统三个SQLServer数据库,在线网站MySQL数据库,记得很早以前是用SessionFactory配置&…...

计算机网络常见题(持续更新中~)
1 描述一下HTTP和HTTPS的区别 2 Cookie和Session有什么区别 3 如果没有Cookie,Session还能进行身份验证吗? 4 BOI,NIO,AIO分别是什么 5 Netty的线程模型是怎么样的 6 Netty是什么?和Tomcat有什么区别,特点是什么? 7 TCP的三次…...

富格林:可信招数揭发防备暗箱陷阱
富格林悉知,在风云变幻的金融市场中,炒贵金属是一项具有高收益潜力的投资方式。但投资是风险与收益共存的,因此我们在做单投资过程中需总结可信招数揭发暗箱陷阱,防备受害亏损。以下总结几点可信的投资技巧,希望能够帮…...
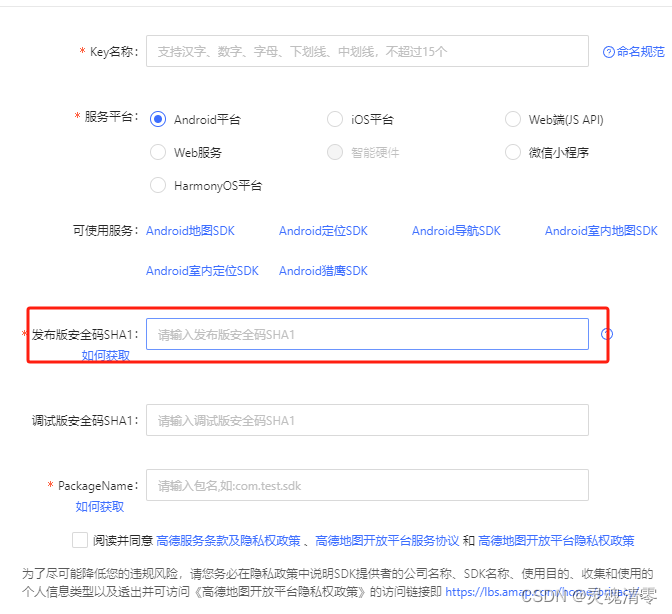
获取高德安全码SHA1
高德开发者平台上给的三种方法 获取安全码SHA1,这里我自己使用的是第三种方法。 1、通过Eclipse编译器获取SHA1 使用 adt 22 以上版本,可以在 eclipse 中直接查看。 Windows:依次在 eclipse 中打开 Window -> Preferances -> Androi…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
