LeetCode 1997.访问完所有房间的第一天:动态规划(DP)——4行主要代码(不需要什么前缀和)
【LetMeFly】1997.访问完所有房间的第一天:动态规划(DP)——4行主要代码(不需要什么前缀和)
力扣题目链接:https://leetcode.cn/problems/first-day-where-you-have-been-in-all-the-rooms/
你需要访问 n 个房间,房间从 0 到 n - 1 编号。同时,每一天都有一个日期编号,从 0 开始,依天数递增。你每天都会访问一个房间。
最开始的第 0 天,你访问 0 号房间。给你一个长度为 n 且 下标从 0 开始 的数组 nextVisit 。在接下来的几天中,你访问房间的 次序 将根据下面的 规则 决定:
- 假设某一天,你访问
i号房间。 - 如果算上本次访问,访问
i号房间的次数为 奇数 ,那么 第二天 需要访问nextVisit[i]所指定的房间,其中0 <= nextVisit[i] <= i。 - 如果算上本次访问,访问
i号房间的次数为 偶数 ,那么 第二天 需要访问(i + 1) mod n号房间。
请返回你访问完所有房间的第一天的日期编号。题目数据保证总是存在这样的一天。由于答案可能很大,返回对 109 + 7 取余后的结果。
示例 1:
输入:nextVisit = [0,0] 输出:2 解释: - 第 0 天,你访问房间 0 。访问 0 号房间的总次数为 1 ,次数为奇数。下一天你需要访问房间的编号是 nextVisit[0] = 0 - 第 1 天,你访问房间 0 。访问 0 号房间的总次数为 2 ,次数为偶数。下一天你需要访问房间的编号是 (0 + 1) mod 2 = 1 - 第 2 天,你访问房间 1 。这是你第一次完成访问所有房间的那天。
示例 2:
输入:nextVisit = [0,0,2] 输出:6 解释: 你每天访问房间的次序是 [0,0,1,0,0,1,2,...] 。 第 6 天是你访问完所有房间的第一天。
示例 3:
输入:nextVisit = [0,1,2,0] 输出:6 解释: 你每天访问房间的次序是 [0,0,1,1,2,2,3,...] 。 第 6 天是你访问完所有房间的第一天。
提示:
n == nextVisit.length2 <= n <= 1050 <= nextVisit[i] <= i
解题方法:动态规划(DP)
题目中明确说明了0 <= nextVisit[i] <= i,也就是说每个房间第一次访问都会“往前回退”到nextVisit[i]而不会访问新的房间,而第二次访问则会访问到“相邻的下一个房间”。
因此我们可以使用一个firstVisit数组,其中firstVisit[i]代表房间i第一次被访问时的天数。
那么,由房间i访问到房间i + 1需要多久呢?
- 首先需要花费一天访问到
nextVisit[i]这个房间(记为j) - 接着需要花费
firstVisit[i] - firstVisit[j]天再一次地由j访问到i - 最后再花费一天由
i访问到i + 1
因此首次访问到房间i + 1的天数为firstVisit[i] + 1 + (firstVisit[i] - firstVisit[j]) + 1 = 2 * firstVisit[i] - firstVisit[j] + 2。
从房间1开始往后遍历到最后一间房间,则firstVisit.back()记为答案。
时空复杂度
- 时间复杂度 O ( l e n ( n e x t V i s i t ) ) O(len(nextVisit)) O(len(nextVisit))
- 空间复杂度 O ( l e n ( n e x t V i s i t ) ) O(len(nextVisit)) O(len(nextVisit))。其实不难发现
nextVisit数组中每个值只会用到一次,因此若将firstVisit保存在nextVisit数组中则可以以 O ( 1 ) O(1) O(1)的空间复杂度实现。
AC代码
C++
typedef long long ll;
const ll MOD = 1e9 + 7;
class Solution {
public:int firstDayBeenInAllRooms(vector<int>& nextVisit) {vector<ll> firstVisit(nextVisit.size());for (int i = 1; i < nextVisit.size(); i++) {firstVisit[i] = (firstVisit[i - 1] * 2 - firstVisit[nextVisit[i - 1]] + 2 + MOD) % MOD; // 记得先加个MOD再对MOD取模,否则可能是负结果。}return firstVisit.back();}
};
Python
from typing import Listclass Solution:def firstDayBeenInAllRooms(self, nextVisit: List[int]) -> int:firstVisit = [0] * len(nextVisit)for i in range(1, len(nextVisit)):firstVisit[i] = (firstVisit[i - 1] * 2 - firstVisit[nextVisit[i - 1]] + 2 + 1_000_000_007) % 1_000_000_007return firstVisit[-1]
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/137119523
相关文章:
——4行主要代码(不需要什么前缀和))
LeetCode 1997.访问完所有房间的第一天:动态规划(DP)——4行主要代码(不需要什么前缀和)
【LetMeFly】1997.访问完所有房间的第一天:动态规划(DP)——4行主要代码(不需要什么前缀和) 力扣题目链接:https://leetcode.cn/problems/first-day-where-you-have-been-in-all-the-rooms/ 你需要访问 n 个房间,房间从 0 到 n - 1 编号。同…...

BootsJS上新!一个库解决大部分难题!
不知不觉距离第一次发文章介绍自己写的库BootsJS已经过去一个月了,这个月里收到了许许多多JYM的反馈与建议,自己也再一次对BootsJS进行了改进与完善,又一次增加了很多功能,为此我想应该给JYM们汇报汇报这个月的工作进展。 BootJS仓…...

智慧公厕,让数据和技术更好服务社会生活
智慧公厕,作为智慧城市建设中不可忽视的一部分,正逐渐受到越来越多人的关注。随着科技的不断进步,智能化公厕已经成为一种趋势,通过数据的流转和技术的整合,为社会生活带来了更好的服务。本文以智慧公厕源头实力厂家广…...
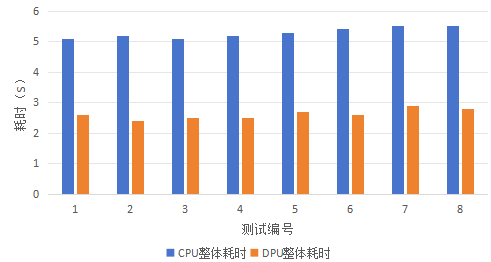
Spark基于DPU Snappy压缩算法的异构加速方案
一、总体介绍 1.1 背景介绍 Apache Spark是专为大规模数据计算而设计的快速通用的计算引擎,是一种与 Hadoop 相似的开源集群计算环境,但是两者之间还存在一些不同之处,这些不同之处使 Spark 在某些工作负载方面表现得更加优越。换句话说&am…...

如何使用python链表
在Python中,可以使用类来实现链表的数据结构。链表是一种数据结构,它由一系列节点组成,每个节点包含一个数据元素和一个指向下一个节点的引用。 下面是一个简单的链表类的示例: class Node:def __init__(self, data):self.data …...

ADB的主要操作命令及详解
ADB,全称Android Debug Bridge,即安卓调试桥,是一个通用的命令行工具,其允许你与模拟器实例或连接的安卓设备进行通信。它可为各种设备操作提供便利,如安装和调试应用,并提供对Unix shell(可用来…...
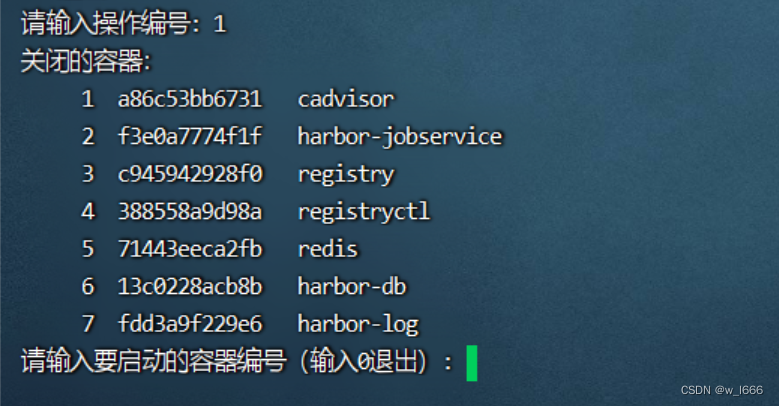
傻瓜式启动关闭重启docker容器的脚本
运行脚本后,界面如下: 选择对应的编号后,会列举所有关闭的容器或者所有开启的容器列表,当我要启动一个容器 时输入1,就会出现下面的页面。 然后输入指定的编号后,就会启动对应的容器。 脚本代码如下&#…...
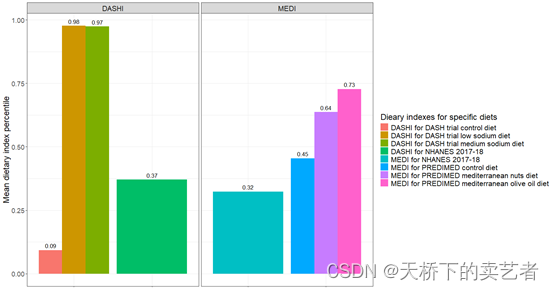
R语言使用dietaryindex包计算NHANES数据多种营养指数(2)
健康饮食指数 (HEI) 是评估一组食物是否符合美国人膳食指南 (DGA) 的指标。Dietindex包提供用户友好的简化方法,将饮食摄入数据标准化为基于指数的饮食模式,从而能够评估流行病学和临床研究中对这些模式的遵守情况,从而促进精准营养。 该软件…...
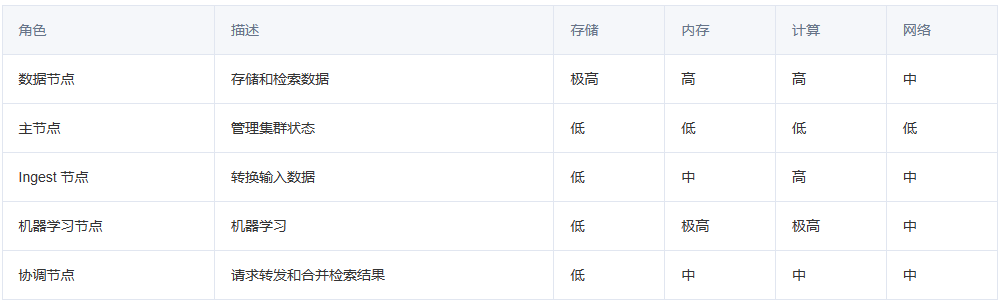
Elasticsearch 索引模板、生命周期策略、节点角色
简介 索引模板可以帮助简化创建和二次配置索引的过程,让我们更高效地管理索引的配置和映射。 索引生命周期策略是一项有意义的功能。它通常用于管理索引和分片的热(hot)、温(warm)和冷(cold)数…...
buy me a btc 使用数字货币进行打赏赞助
最近在调研使用加密货币打赏的平台,发现idatariver平台 https://idatariver.com 推出的buymeabtc功能刚好符合使用场景,下图为平台的演示项目, 演示项目入口 https://buymeabtc.com/idatariver 特点 不少人都听说过buymeacoffee,可以在上面发…...
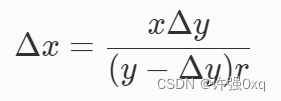
Solidity Uniswap V2 Router swapTokensForExactTokens
最初的router合约实现了许多不同的交换方式。我们不会实现所有的方式,但我想向大家展示如何实现倒置交换:用未知量的输入Token交换精确量的输出代币。这是一个有趣的用例,可能并不常用,但仍有可能实现。 GitHub - XuHugo/solidit…...

网络安全渗透测试工具
网络安全渗透测试常用的开发工具包括但不限于以下几种: Nmap:一款网络扫描工具,用于探测目标主机的开放端口和正在运行的服务,是网络发现和攻击界面测绘的首选工具。Wireshark:一个流量分析工具,用于监测网…...
springcloud+nacos服务注册与发现
快速开始 | Spring Cloud Alibaba 参考官方快速开始教程写的,主要注意引用的包是否正确。 这里是用的2022.0.0.0-RC2版本的springCloud,所以需要安装jdk21,参考上一个文章自行安装。 nacos-config实现配置中心功能-CSDN博客 将nacos-conf…...

【C++程序员的自我修炼】基础语法篇(一)
心中若有桃花源 何处不是水云间 目录 命名空间 💞命名空间的定义 💞 命名空间的使用 输入输出流 缺省参数 函数的引用 引用的定义💞 引用的表示💞 引用的特性💞 常量引用💞 引用的使用场景 做参数 做返回值…...
小狐狸JSON-RPC:钱包连接,断开连接,监听地址改变
detect-metamask 创建连接,并监听钱包切换 一、连接钱包,切换地址(监听地址切换),断开连接 使用npm安装 metamask/detect-provider在您的项目目录中: npm i metamask/detect-providerimport detectEthereu…...

union在c语言中什么用途
在C语言中,union是一种特殊的数据类型,可以在同一块内存中存储不同类型的数据。它的主要用途有以下几个: 1. 节省内存:由于union只占用其成员中最大的数据类型所占用的内存空间,可以在不同的情况下使用同一块内存来存…...
)
2024年华为OD机试真题- 寻找最优的路测线路-Java-OD统一考试(C卷)
题目描述: 评估一个网络的信号质量,其中一个做法是将网络划分为栅格,然后对每个栅格的信号质量计算。路测的时候,希望选择一条信号最好的路线(彼此相连的栅格集合)进行演示。现给出R行C列的整数数组Cov,每个单元格的数值S即为该栅格的信号质量(已归一化,无单位,值越大…...

WPF 多路绑定、值转换器ValueConvert、数据校验
值转换器 valueconvert 使用ValueConverter需要实现IValueConverter接口,其内部有两个方法,Convert和ConvertBack。我们在使用Binding绑定数据的时候,当遇到源属性和目标控件需要的类型不一致的,就可以使用ValueConverter…...
【Linux多线程】线程的同步与互斥
【Linux多线程】线程的同步与互斥 目录 【Linux多线程】线程的同步与互斥分离线程Linux线程互斥进程线程间的互斥相关背景概念问题产生的原因: 互斥量mutex互斥量的接口互斥量实现原理探究对锁进行封装(C11lockguard锁) 可重入VS线程安全概念常见的线程不安全的情况…...

Linux网卡bond的七种模式详解
像Samba、Nfs这种共享文件系统,网络的吞吐量非常大,就造成网卡的压力很大,网卡bond是通过把多个物理网卡绑定为一个逻辑网卡,实现本地网卡的冗余,带宽扩容和负载均衡,具体的功能取决于采用的哪种模式。 Lin…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...
