递归方法的理解
public void methodA (){methodA ();}
间接递归:可以理解为A()方法调用B()方法,B()方法调用C()方法,C()方法调用A()方法。
public static void A (){B ();}public static void B (){C ();}public static void C (){A ();}
举例1:计算1 ~ n的和
public class RecursionDemo {public static void main ( String [] args ) {RecursionDemo demo = new RecursionDemo ();// 计算 1~num 的和,使用递归完成int num = 5 ;// 调用求和的方法int sum = demo . getSum ( num );// 输出结果System . out . println ( sum );}/*通过递归算法实现 .参数列表 :int返回值类型 : int*/public int getSum ( int num ) {/*num 为 1 时 , 方法返回 1,相当于是方法的出口 ,num 总有是 1 的情况*/if ( num == 1 ){return 1 ;}/*num 不为 1 时 , 方法返回 num +(num-1) 的累和递归调用 getSum 方法*/return num + getSum ( num - 1 );}}
代码执行图解:
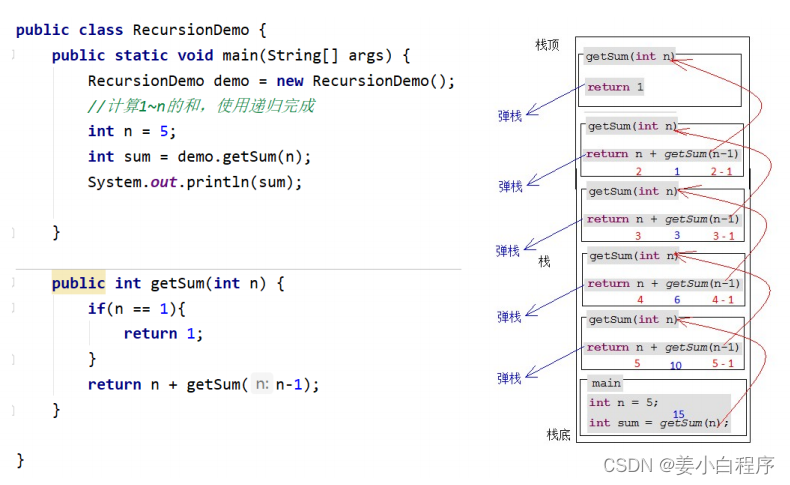
代码解释
/* * 当程序执行时,它会按照以下流程进行:1. `main` 方法被调用。 2. 一个 `RecursionDemo` 类的对象 `demo` 被创建。 3. `n` 被赋值为 5。 4. 调用 `demo.getSum(n)` 方法,其中 `n` 的值为 5。 5. 进入 `getSum` 方法。 6. `n` 的值不为 1,因此程序执行 `return n + getSum(n - 1);`,其中 `n - 1` 的值为 4。 7. 程序递归调用 `getSum` 方法,将参数值 `4` 传递给它。 8. 再次进入 `getSum` 方法。 9. `n` 的值不为 1,因此程序执行 `return n + getSum(n - 1);`,其中 `n - 1` 的值为 3。 10. 程序递归调用 `getSum` 方法,将参数值 `3` 传递给它。 11. 再次进入 `getSum` 方法。 12. `n` 的值不为 1,因此程序执行 `return n + getSum(n - 1);`,其中 `n - 1` 的值为 2。 13. 程序递归调用 `getSum` 方法,将参数值 `2` 传递给它。 14. 再次进入 `getSum` 方法。 15. `n` 的值不为 1,因此程序执行 `return n + getSum(n - 1);`,其中 `n - 1` 的值为 1。 16. 程序递归调用 `getSum` 方法,将参数值 `1` 传递给它。 17. 再次进入 `getSum` 方法。 18. `n` 的值为 1,因此程序直接返回 1。 19. 回到上一层递归调用,将返回的值 1 加上当前层的 `n` 的值(为 2),得到结果 3,返回给上一层。 20. 继续返回上一层递归调用,将返回的值 3 加上当前层的 `n` 的值(为 3),得到结果 6,返回给上一层。 21. 继续返回上一层递归调用,将返回的值 6 加上当前层的 `n` 的值(为 4),得到结果 10,返回给上一层。 22. 继续返回上一层递归调用,将返回的值 10 加上当前层的 `n` 的值(为 5),得到结果 15,返回给上一层。 23. 回到 `main` 方法,将返回的结果 15 赋值给 `sum` 变量。 24. `System.out.println(sum);` 将结果打印到控制台上。所以,程序的输出结果为 `15`。 * * * * */ }
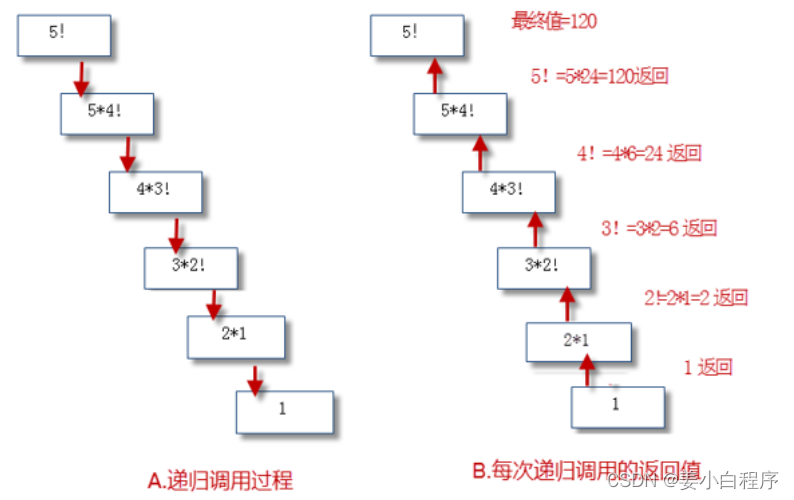
举例2:递归方法计算n!
public int multiply ( int num ){if ( num == 1 ){return 1 ;} else {return num * multiply ( num - 1 );}}
public int f ( int num ){if ( num == 0 ){return 1 ;} else if ( num == 1 ){return 4 ;} else {return 2 * f ( num - 1 ) + f ( num - 2 );}}
举例3:已知有一个数列:f(0) = 1,f(1) = 4,f(n+2)=2*f(n+1) + f(n),其中n是大于0的整数,求f(10)的值。
public int func ( int num ){if ( num == 20 ){return 1 ;} else if ( num == 21 ){return 4 ;} else {return func ( num + 2 ) - 2 * func ( num + 1 );}}
举例4:计算斐波那契数列(Fibonacci)的第n个值
// 使用递归的写法int f ( int n ) { // 计算斐波那契数列第 n 个值是多少if ( n < 1 ) { // 负数是返回特殊值 1 ,表示不计算负数情况return 1 ;}if ( n == 1 || n == 2 ) {return 1 ;}return f ( n - 2 ) + f ( n - 1 );}// 不用递归int fValue ( int n ) { // 计算斐波那契数列第 n 个值是多少if ( n < 1 ) { // 负数是返回特殊值 1 ,表示不计算负数情况return 1 ;}if ( n == 1 || n == 2 ) {return 1 ;}// 从第三个数开始, 等于 前两个整数相加int beforeBefore = 1 ; // 相当于 n=1 时的值int before = 1 ; // 相当于 n=2 时的值int current = beforeBefore + before ; // 相当于 n=3 的值// 再完后for ( int i = 4 ; i <= n ; i ++ ) {beforeBefore = before ;before = current ;current = beforeBefore + before ;/* 假设 i=4beforeBefore = before; // 相当于 n=2 时的值before = current; // 相当于 n=3 的值current = beforeBefore + before; // 相当于 n = 4 的值假设 i=5beforeBefore = before; // 相当于 n=3 的值before = current; // 相当于 n = 4 的值current = beforeBefore + before; // 相当于 n = 5 的值....*/}return current ;}
举例5:面试题
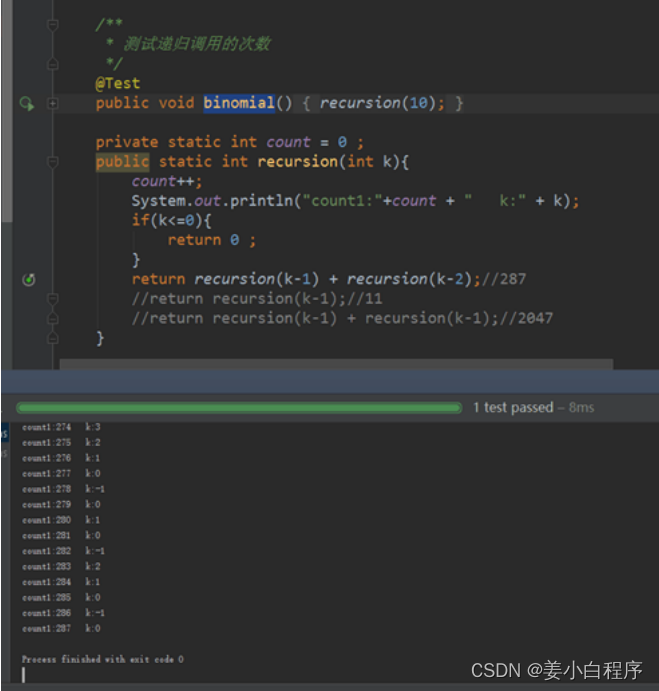
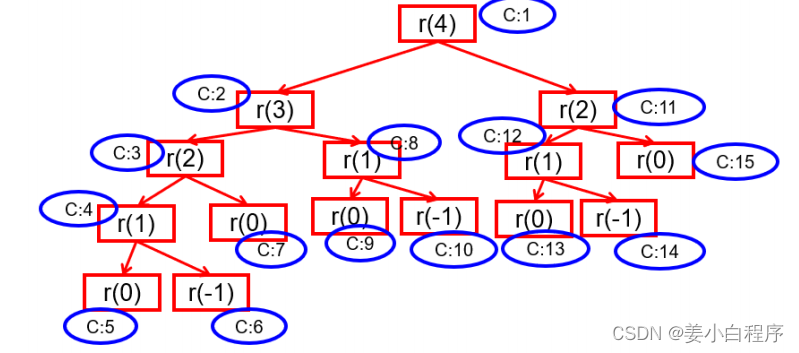
private int count = 0 ;public int recursion ( int k ) {count ++ ;System . out . println ( "count1:" + count + " k:" + k );if ( k <= 0 ) {return 0 ;}return recursion ( k - 1 ) + recursion ( k - 2 ); //287//return recursion(k - 1);//11//return recursion(k - 1) + recursion(k - 1);//2047}
剖析:
最后说两句:1. 递归调用会占用大量的系统堆栈,内存耗用多,在递归调用层次多时速度要比循环 慢的多 ,所以在使用递归时要慎重。2. 在要求高性能的情况下尽量避免使用递归,递归调用既花时间又 耗内存 。考虑使用循环迭 代。
相关文章:

递归方法的理解
递归方法调用 :方法自己调用自己的现象就称为递归。 递归的分类 : 直接递归、间接递归。 直接递归:方法自身调用自己 public void methodA (){ methodA (); } 间接递归:可以理解为A()方法调用B()方法,B()方法调用C()方法&am…...

css之flex布局文本不换行不显示省略号的解决方法
文章目录 一、单行长文本显示省略号二、flex布局下的处理技巧 一、单行长文本显示省略号 先讲讲常规情况下长文本不跨行显示省略号的代码: overflow: hidden; //不允许内容超出盒子 white-space: nowrap; //不允许文本跨行 text-overflow: ellipsis; //文本超…...

华清远见STM32U5开发板助力2024嵌入式大赛ST赛道智能可穿戴设备及IOT选题项目开发
第七届(2024)全国大学生嵌入式芯片与系统设计竞赛(以下简称“大赛”)已经拉开帷幕,大赛的报名热潮正席卷而来,高校电子电气类相关专业(电子、信息、计算机、自动化、电气、仪科等)全…...
若依框架实现不同端用户登录(后台管理用户和前台会员登录——sping security多用户)
目录 需求背景 前期准备 实现UserDetailsService接口 改造loginUser 声明自定义AuthenticationManager 的bean 自定义登录接口 参考文章 效果如下 需求背景 用若依搭建的后台管理环境,但是前台用户系统(前端)并没有和若依的前端集成在一起。…...

【解決|三方工具】Obi Rope 编辑器运行即崩溃问题
开发平台:Unity 2021.3.7 三方工具:Unity资产工具 - Obi Rope 问题背景 使用Unity三方开发工具 - Obi Rope 模拟绳索效果。配置后运行 Unity 出现报错并崩溃。通过崩溃日志反馈得到如下图所示 这是一个序列化问题造成的崩溃,指向性为 Obi…...
岭师大数据技术原理与应用-序章-软工版
HeZaoCha-CSDN博客 序章—软工版 一、环境介绍1. VMware Workstation Pro2. CentOS3. Java4. Hadoop5. HBase6. MySQL7. Hive 二、系统安装1. 虚拟网络编辑器2. 操作系统安装 三、结尾 先说说哥们写这系列博客的原因,本来学完咱也没想着再管部署这部分问题的说&…...

Leetcode 680. 验证回文串 II
给你一个字符串 s,最多 可以从中删除一个字符。 请你判断 s 是否能成为回文字符串:如果能,返回 true ;否则,返回 false 。 示例 1: 输入:s “aba” 输出:true 示例 2:…...
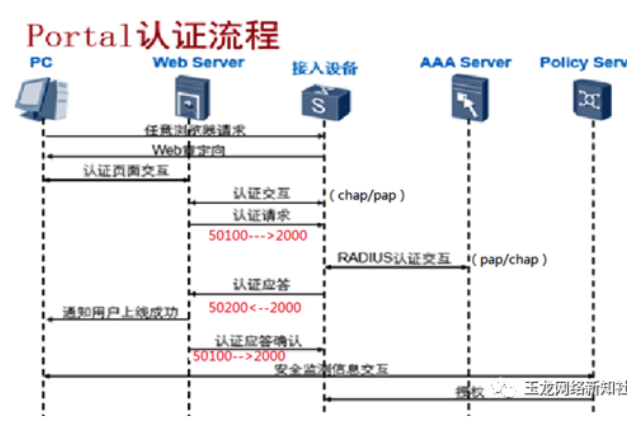
网络安全接入认证-802.1X接入说明
介绍 802.1X是一个网络访问控制协议,它可以通过认证和授权来控制网络访问。它的基本原理是在网络交换机和认证服务器之间建立一个安全的通道,并要求客户端提供身份验证凭据。如果客户端提供的凭据是有效的,交换机将开启端口并允许访问。否则&…...

iPhone的iOS系统:定义移动智能体验,引领科技潮流之巅
来自:dlshuhua.com/post/83721.html 在移动智能设备领域,iPhone一直以其出色的性能和独特的用户体验脱颖而出。而这一切的背后,离不开其强大的操作系统——iOS。iOS系统不仅为iPhone提供了强大的性能支持,更通过不断创新和升级&a…...
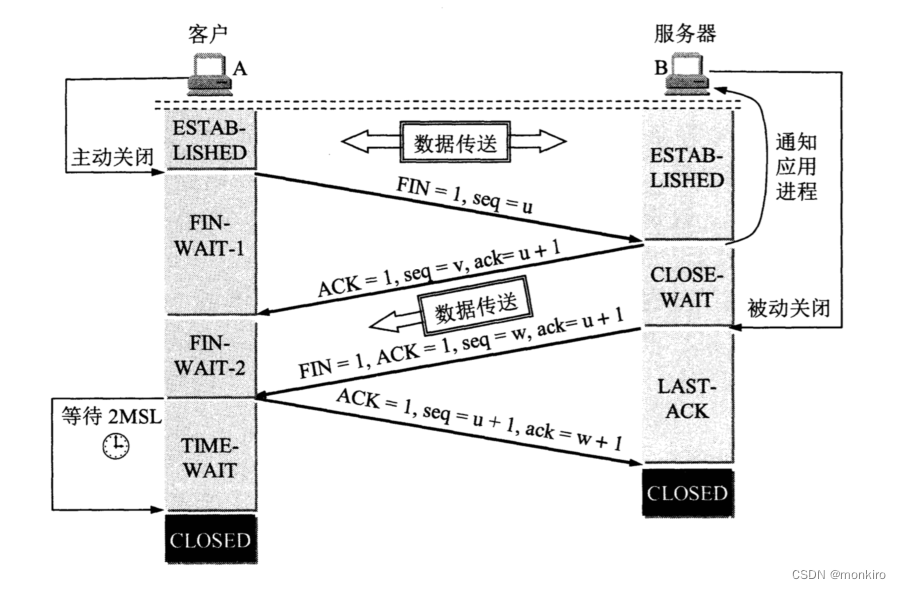
计算机网络:传输控制协议(Transmission Control Protocol-TCP协议
计算机网络:传输控制协议(Transmission Control Protocol-TCP协议) 本文目的前置知识点TCP协议简介主要特性通信流程1. 建立连接的过程(三次握手,243)1.1 为什么要三次握手,两次不行吗? 2. 释放连接的过程(…...
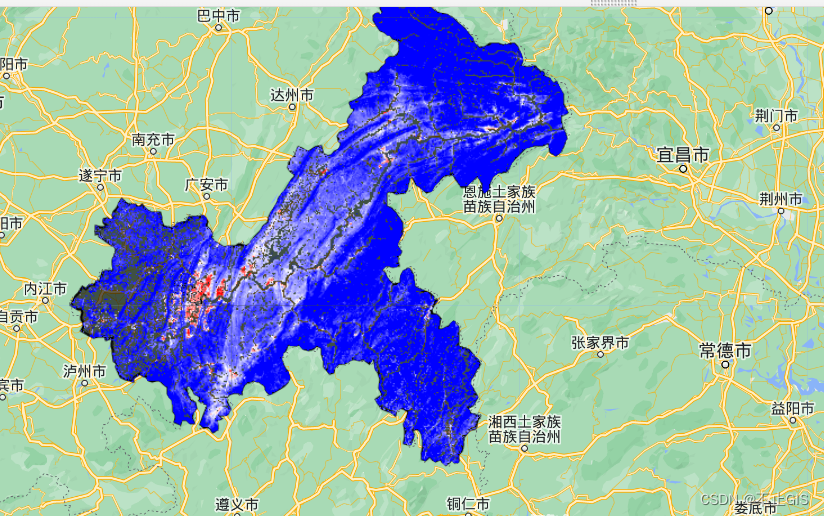
GEE实践应用|热岛效应(一)地表温度计算
目录 1.学习目标 2.理论介绍 3.从MODIS获得地表温度 4.从Landsat卫星获得地表温度 1.学习目标 ①了解如何使用GEE计算地表温度 2.理论介绍 城市化涉及用建筑物、道路和停车场等建筑结构取代自然景观。这种土地覆盖的改变也改变了土地表面的特性。这些变化的范围从表面反射和…...
)
Java查找算法知识点(含面试大厂题和源码)
查找算法是计算机科学中的基础概念,它们在解决实际问题时扮演着关键角色。了解和掌握不同的查找算法,能够帮助我们更高效地处理数据检索任务。以下是一些关于查找算法的关键知识点: 算法分类: 线性查找算法:按照顺序逐…...

67、yolov8目标检测和旋转目标检测算法部署Atlas 200I DK A2开发板上
基本思想:需求部署yolov8目标检测和旋转目标检测算法部署atlas 200dk 开发板上 一、转换模型 链接: https://pan.baidu.com/s/1hJPX2QvybI4AGgeJKO6QgQ?pwdq2s5 提取码: q2s5 from ultralytics import YOLO# Load a model model YOLO("yolov8s.yaml")…...
A Little Is Enough: Circumventing Defenses For Distributed Learning
联邦学习的攻击方法:LIE 简单的总结,只是为了能快速想起来这个方法。 无目标攻击 例如总共50个客户端,有24个恶意客户端,那么这个时候,他需要拉拢2个良性客户端 计算 50 − 24 − 2 50 − 24 0.923 \frac{50-24-2}{…...

文心一言 VS 讯飞星火 VS chatgpt (225)-- 算法导论16.3 7题
七、推广赫夫曼算法,使之能生成三进制的码字(即码字由符号0、1、2组成),并证明你的算法能生成最优三进制码。如果要写代码,请用go语言。 文心一言: 推广赫夫曼算法以生成三进制码字需要对算法进行一定的修改,确保在每…...

【计算机】——51单片机——持续更新
单片机是一种内部包含CPU、存储器和输入/输出接口等电路的集成电路(IC芯片) 单片机是单片微型计算机(Single Chip Microcomputer)的简称,用于控制领域,所以又称为微型控制器(Microcontroller U…...
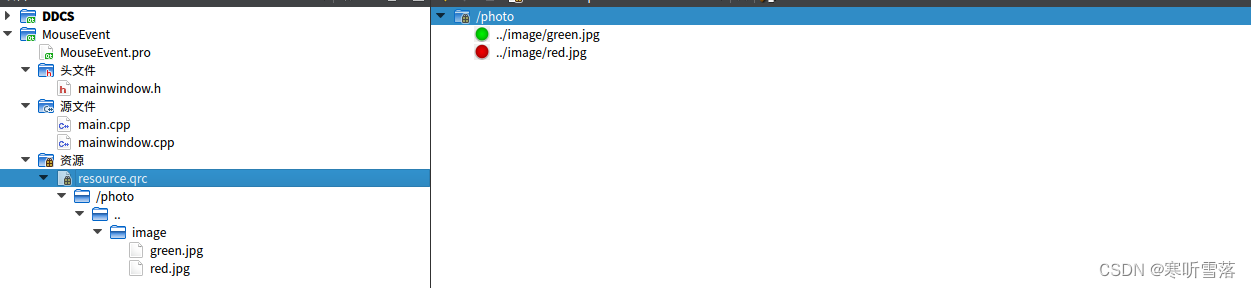
QT资源添加调用
添加资源文件,新建资源文件夹,命名resource,然后点下一步,点完成 资源,右键add Prefix 添加现有文件 展示的label图片切换 QLabel *led_show; #include "mainwindow.h" #include<QLabel> #include&l…...

LeetCode-49. 字母异位词分组【数组 哈希表 字符串 排序】
LeetCode-49. 字母异位词分组【数组 哈希表 字符串 排序】 题目描述:解题思路一:哈希表和排序,这里最关键的点是,乱序单词的排序结果必然是一样的(从而构成哈希表的key)。解题思路二:解题思路三…...

绘制特征曲线-ROC(Machine Learning 研习十七)
接收者操作特征曲线(ROC)是二元分类器的另一个常用工具。它与精确度/召回率曲线非常相似,但 ROC 曲线不是绘制精确度与召回率的关系曲线,而是绘制真阳性率(召回率的另一个名称)与假阳性率(FPR&a…...

.Net 知识杂记
记录平日中琐碎的.net 知识点。不定期更新 目标框架名称(TFM) 我们创建C#应用程序时,在项目的工程文件(*.csproj)中都有targetFramework标签,以表示项目使用的目标框架 各种版本的TFM .NET Framework .NET Standard .NET5 及更高版本 UMP等 参考文档&a…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...
