Python学习笔记-简单案例实现多进程与多线程
Python 的多进程与多线程是并发编程的两种重要方式,用于提高程序的执行效率。它们各自有不同的特点和适用场景。
多进程(Multiprocessing)
概念:
多进程是指操作系统中同时运行多个程序实例,每个实例称为一个进程。每个进程都拥有独立的内存空间和系统资源。
特点:
- 独立性:每个进程拥有独立的内存地址空间,互不干扰。
- 稳定性:一个进程的崩溃不会影响其他进程的运行。
- 资源消耗:创建和切换进程的开销较大,因为需要为每个进程分配内存和其他系统资源。
- 数据共享:进程间通信(IPC)需要通过特定的机制来实现,如管道、消息队列、共享内存等。
适用场景:
- CPU 密集型任务,即计算密集型任务,适合使用多进程,因为可以利用多核 CPU 的并行计算能力。
- 需要高稳定性的场景,如服务器后端,一个进程的崩溃不会导致整个服务停止。
代码实现:
1.导包

2.创建进程对象

3.启动进程执行任务
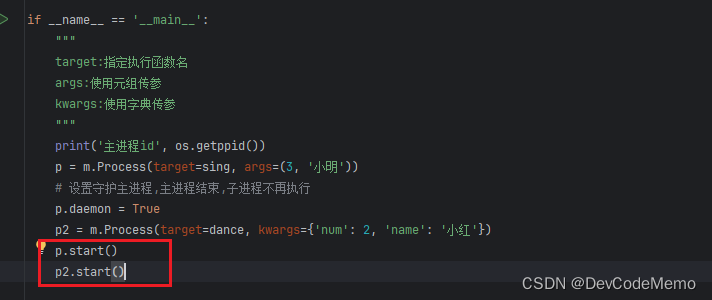
源码:
import os
import time
import multiprocessing as mdef sing(num, name):print('子进程id', os.getpid())print('子进程的父id', os.getppid())for i in range(num):print('%s唱歌...%d次' % (name, i + 1))time.sleep(0.5)def dance(num, name):for i in range(num):print(f'{name}跳舞...')time.sleep(0.5)if __name__ == '__main__':"""target:指定执行函数名args:使用元组传参kwargs:使用字典传参"""print('主进程id', os.getppid())p = m.Process(target=sing, args=(3, '小明'))# 设置守护主进程,主进程结束,子进程不再执行p.daemon = Truep2 = m.Process(target=dance, kwargs={'num': 2, 'name': '小红'})p.start()p2.start()
多线程(Multithreading)
概念:
多线程是指在同一个进程中并发执行多个线程,共享进程的内存空间和系统资源。
特点:
- 共享性:线程间共享进程的内存空间和系统资源。
- 开销小:创建和切换线程的开销通常比进程小。
- 全局解释器锁(GIL):在 CPython 解释器中,由于全局解释器锁(GIL)的存在,多线程在 CPU 密集型任务中并不能实现真正的并行执行,只能实现并发。但在 I/O 密集型任务中,多线程可以有效提高程序的响应速度。
- 数据同步:多线程间共享数据可能导致数据不一致,因此需要使用锁、条件变量等同步机制来确保数据的正确性。
适用场景:
- I/O 密集型任务,如网络请求、文件读写等,多线程可以提高程序的响应速度和吞吐量。
- 需要共享数据的场景,多线程可以方便地访问和修改共享数据。
代码实现:
1.导包
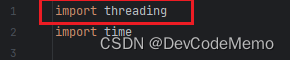
2.创建线程对象
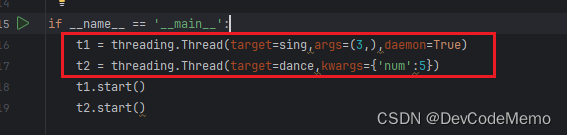
3.启动线程执行任务

源码:
import threading
import timedef sing(num):for i in range(num):print('唱歌...')time.sleep(0.2)
def dance(num):for i in range(num):print('跳舞...')time.sleep(0.2)if __name__ == '__main__':t1 = threading.Thread(target=sing,args=(3,),daemon=True)t2 = threading.Thread(target=dance,kwargs={'num':5})t1.start()t2.start()总结
多进程和多线程各有优劣,选择哪种方式取决于具体的应用场景和需求。对于 CPU 密集型任务,通常使用多进程;对于 I/O 密集型任务或需要共享数据的场景,多线程可能更合适。在实际开发中,还可以考虑使用进程池和线程池来管理和控制并发数量,以提高系统的稳定性和性能。
相关文章:

Python学习笔记-简单案例实现多进程与多线程
Python 的多进程与多线程是并发编程的两种重要方式,用于提高程序的执行效率。它们各自有不同的特点和适用场景。 多进程(Multiprocessing) 概念: 多进程是指操作系统中同时运行多个程序实例,每个实例称为一个进程。…...

python常用的语法
Python是一种高级、通用、解释型的编程语言,具有简洁、易于阅读和理解的语法。以下是Python中常用的语法: 变量定义和赋值: variable value输出内容: print("Hello, World!")条件判断: if condition:# 条件…...

【计算机网络】概述
📝本文介绍 本文为计算机网络的概述,会综合概述一下计算机网络 👋作者简介:一个正在积极探索的本科生 📱联系方式:943641266(QQ) 🚪Github地址:https://github.com/sankexilianhua &…...
实战举例)
【Flink connector】文件系统 SQL 连接器:实时写文件系统以及(kafka到hive)实战举例
文章目录 一. 滚动策略:sink后文件切分(暂不关注)1. 切分分区目录下的文件2. 小文件合并 二. 分区提交1. 分区提交触发器 (什么时候创建分区)1.1. 逻辑说明1.2. 举例说明 2. 分区时间提取器 (用于partition-time情况下partition commit策略)2…...

RpcContext :提供了在 RPC 调用过程中访问当前调用信息的方法
在 Dubbo 中,RpcContext 是一个上下文对象,它提供了在 RPC 调用过程中访问当前调用信息的方法。RpcContext.getClientAttachment() 方法用于获取客户端设置的附件(Attachment)信息。这些附件信息通常是在 RPC 调用发起方ÿ…...
)
机器学习 - 提高模型 (代码)
如果模型出现了 underfitting 问题,就得提高模型了。 Model improvement techniqueWhat does it do?Add more layersEach layer potentially increases the learning capabilities of the model with each layer being able to learn some kind of new pattern in…...

数值代数及方程数值解:预备知识——二进制及浮点数
文章目录 二进制IEEE浮点数 本篇文章的前置知识:数学分析 二进制 命题:二进制转化为十进制 二进制的数字表示为 ⋯ b 2 b 1 b 0 . b − 1 b − 2 ⋯ \cdots b_2b_1b_0.b_{-1}b_{-2}\cdots ⋯b2b1b0.b−1b−2⋯这等价于十进制下的 ⋯ b 2 2 …...

新数字时代的启示:揭开Web3的秘密之路
在当今数字时代,随着区块链技术的不断发展,Web3作为下一代互联网的概念正逐渐引起人们的关注和探索。本文将深入探讨新数字时代的启示,揭开Web3的神秘之路,并探讨其在未来的发展前景。 1. Web3的定义与特点 Web3是对互联网未来发…...

算法——动态规划:01背包
原始01背包见下面这篇文章:http://t.csdnimg.cn/a1kCL 01背包的变种:. - 力扣(LeetCode) 给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。 简化一…...

写作类AI推荐(二)
本章要介绍的写作AI如下: 火山写作 主要功能: AI智能创作:告诉 AI 你想写什么,立即生成你理想中的文章AI智能改写:选中段落句子,可提升表达、修改语气、扩写、总结、缩写等文章内容优化:根据全文…...
(JAVA))
分寝室(20分)(JAVA)
目录 题目描述 输入格式: 输出格式: 输入样例 1: 输出样例 1: 输入样例 2: 输出样例 2: 题解: 题目描述 学校新建了宿舍楼,共有 n 间寝室。等待分配的学生中,有女…...

Spring 源码调试问题 ( List.of(“bin“, “build“, “out“); )
Spring 源码调试问题 文章目录 Spring 源码调试问题一、问题描述二、解决方案 一、问题描述 错误:springframework\buildSrc\src\main\java\org\springframework\build\CheckstyleConventions.java:68: 错误: 找不到符号 List<String> buildFolders List.of…...
Centos7安装RTL8111网卡驱动
方法一: // 安装pciutils # yum install -y pciutils // 查看pci设备信息 # lspci | grep -i Ethernet 09:00.0 Ethernet controller: Realtek Semiconductor Co., Ltd. RTL8111/8168/8411 PCI Express Gigabit Ethernet Controller (rev 03) // 上面看到是Re…...

吉时利KEITHLEY2460数字源表
181/2461/8938产品概述: Keithley 2460 高电流源表源测量单元 (SMU) 将先进的触摸、测试和发明技术带到您的指尖。Keithley 2460 将创新的图形用户界面 (GUI) 与电容式触摸屏技术相结合,使测试变得直观并最大限度地缩短学习曲线,从而帮助工程…...
)
数据库原理(含思维导图)
数据库原理笔记,html与md笔记已上传 1.绪论 发展历程 记住数据怎么保存,谁保存数据,共享性如何,独立性如何 人工管理阶段 数据不保存应用程序管理数据数据不共享数据不具有独立性 文件系统阶段 数据可以长期保存文件系统管…...

数据结构(六)——图
六、图 6.1 图的基本概念 图的定义 图:图G由顶点集V和边集E组成,记为G (V, E),其中V(G)表示图G中顶点的有限非空集;E(G) 表示图G中顶点之间的关系(边)集合。若V {v1, v2, … , vn},则用|V|…...

Android-AR眼镜屏幕显示
Android-AR眼镜 前提:Android手持设备 需要具备DP高清口 1、创建Presentation(双屏异显) public class MyPresentation extends Presentation {private PreviewSingleBinding binding;private ScanActivity activity;public MyPresentatio…...

蓝桥集训之货币系统
蓝桥集训之货币系统 核心思想:背包 #include <iostream>#include <cstring>#include <algorithm>using namespace std;const int N 30,M 10010;typedef long long LL;LL f[M];int w[N];int n,m;int main(){cin>>n>>m;for(int i1;i&…...

基于微信小程序的校园服务平台设计与实现(程序+论文)
本文以校园服务平台为研究对象,首先分析了当前校园服务平台的研究现状,阐述了本系统设计的意义和背景,运用微信小程序开发工具和云开发技术,研究和设计了一个校园服务平台,以满足学生在校园生活中的多样化需求。通过引…...
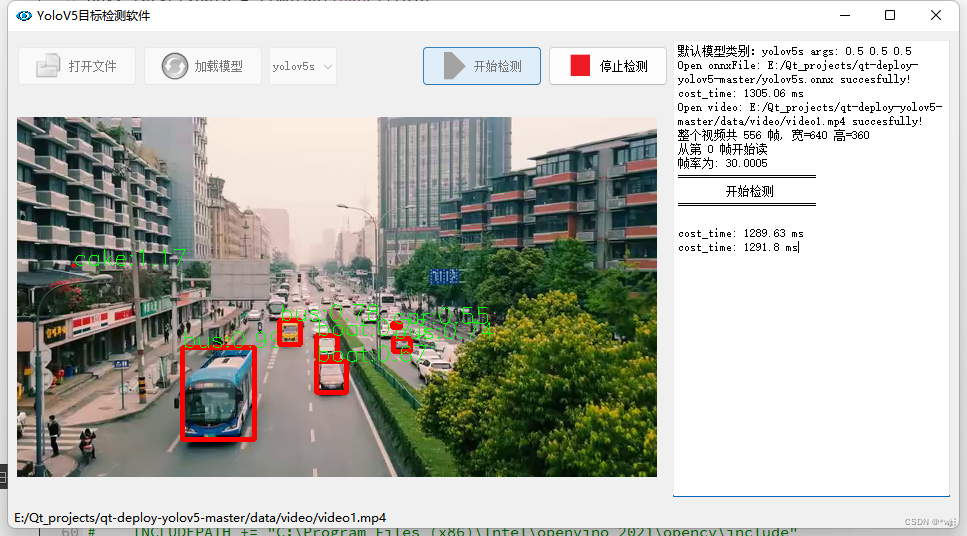
QT+Opencv+yolov5实现监测
功能说明:使用QTOpencvyolov5实现监测 仓库链接:https://gitee.com/wangyoujie11/qt_yolov5.git git本仓库到本地 一、环境配置 1.opencv配置 将OpenCV-MinGW-Build-OpenCV-4.5.2-x64文件夹放在自己的一个目录下,如我的路径: …...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
