动态规划相关题目
文章目录
- 1.动态规划理论基础
- 2.斐波那契数
- 3.爬楼梯
- 4.使用最小花费爬楼梯
- 5.不同路径
- 6.不同路径 II
- 7. 整数拆分
- 8. 不同的二叉搜索树
1.动态规划理论基础
1.1 什么是动态规划?
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的。
1.2 动态规划的解题步骤
动态规划五部曲:
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
2.斐波那契数
题目:

思路:
状态转移方程 dp[i] = dp[i - 1] + dp[i - 2]
代码:
class Solution:def fib(self, n: int) -> int:# 排除 Corner Caseif n == 0:return 0# 创建 dp table dp = [0] * (n + 1)# 初始化 dp 数组dp[0] = 0dp[1] = 1# 遍历顺序: 由前向后。因为后面要用到前面的状态for i in range(2, n + 1):# 确定递归公式/状态转移公式dp[i] = dp[i - 1] + dp[i - 2]# 返回答案return dp[n]
3.爬楼梯
题目:

思路:
递推公式dp[i] = dp[i - 1] + dp[i - 2]
代码:
class Solution:def climbStairs(self, n: int) -> int:if n == 1:return 1if n == 2:return 2dp = [0] * (n + 1)dp[1] = 1dp[2] = 2for i in range(3,n+1):dp[i] = dp[i - 2] + dp[i-1]return dp[n]
4.使用最小花费爬楼梯
题目:

思路:
dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。
递推公式:
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
注:楼顶的下标是n+1
代码:
class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:dp = [0] * (len(cost) + 1)# dp[0] = 0 # 初始值,表示从起点开始不需要花费体力# dp[1] = 0 # 初始值,表示经过第一步不需要花费体力for i in range(2, len(cost) + 1):# 在第i步,可以选择从前一步(i-1)花费体力到达当前步,或者从前两步(i-2)花费体力到达当前步# 选择其中花费体力较小的路径,加上当前步的花费,更新dp数组dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])return dp[len(cost)] # 返回到达楼顶的最小花费
5.不同路径
题目:
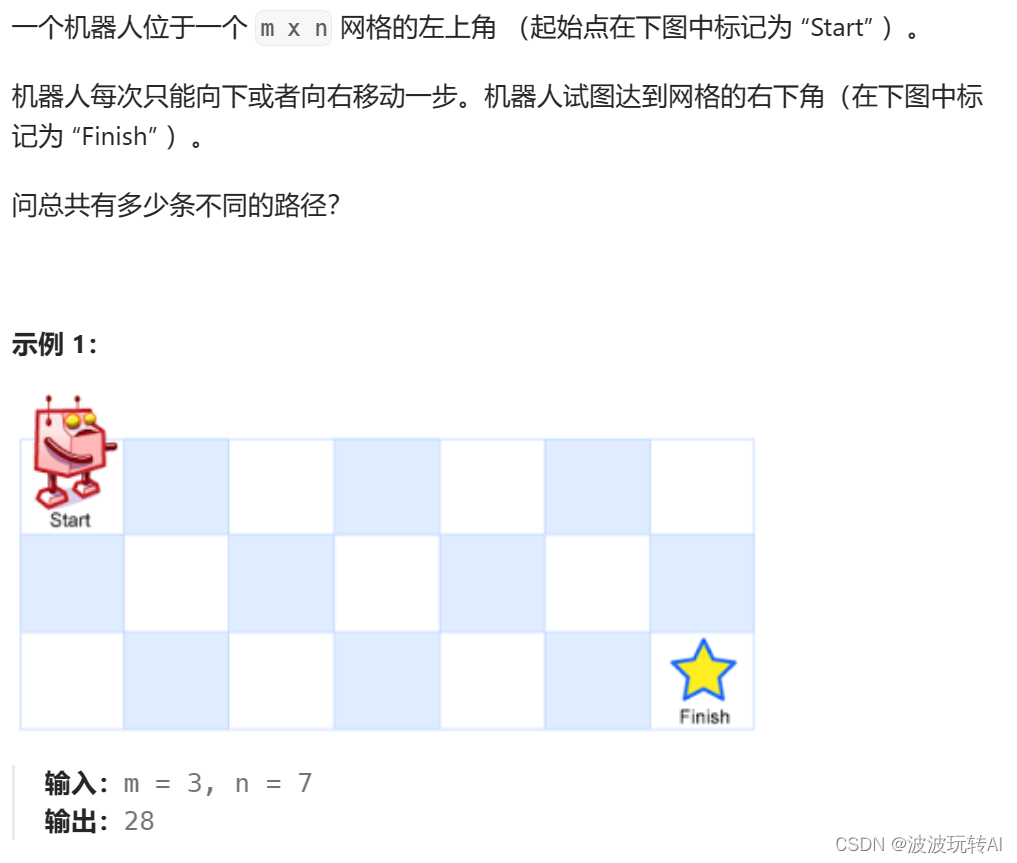
思路:
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
递推公式:dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
如何初始化呢,首先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。
代码:
class Solution:def uniquePaths(self, m: int, n: int) -> int:# 创建一个二维列表用于存储唯一路径数dp = [[0] * n for _ in range(m)]# 设置第一行和第一列的基本情况for i in range(m):dp[i][0] = 1for j in range(n):dp[0][j] = 1# 计算每个单元格的唯一路径数for i in range(1, m):for j in range(1, n):dp[i][j] = dp[i - 1][j] + dp[i][j - 1]# 返回右下角单元格的唯一路径数return dp[m - 1][n - 1]
6.不同路径 II
题目:
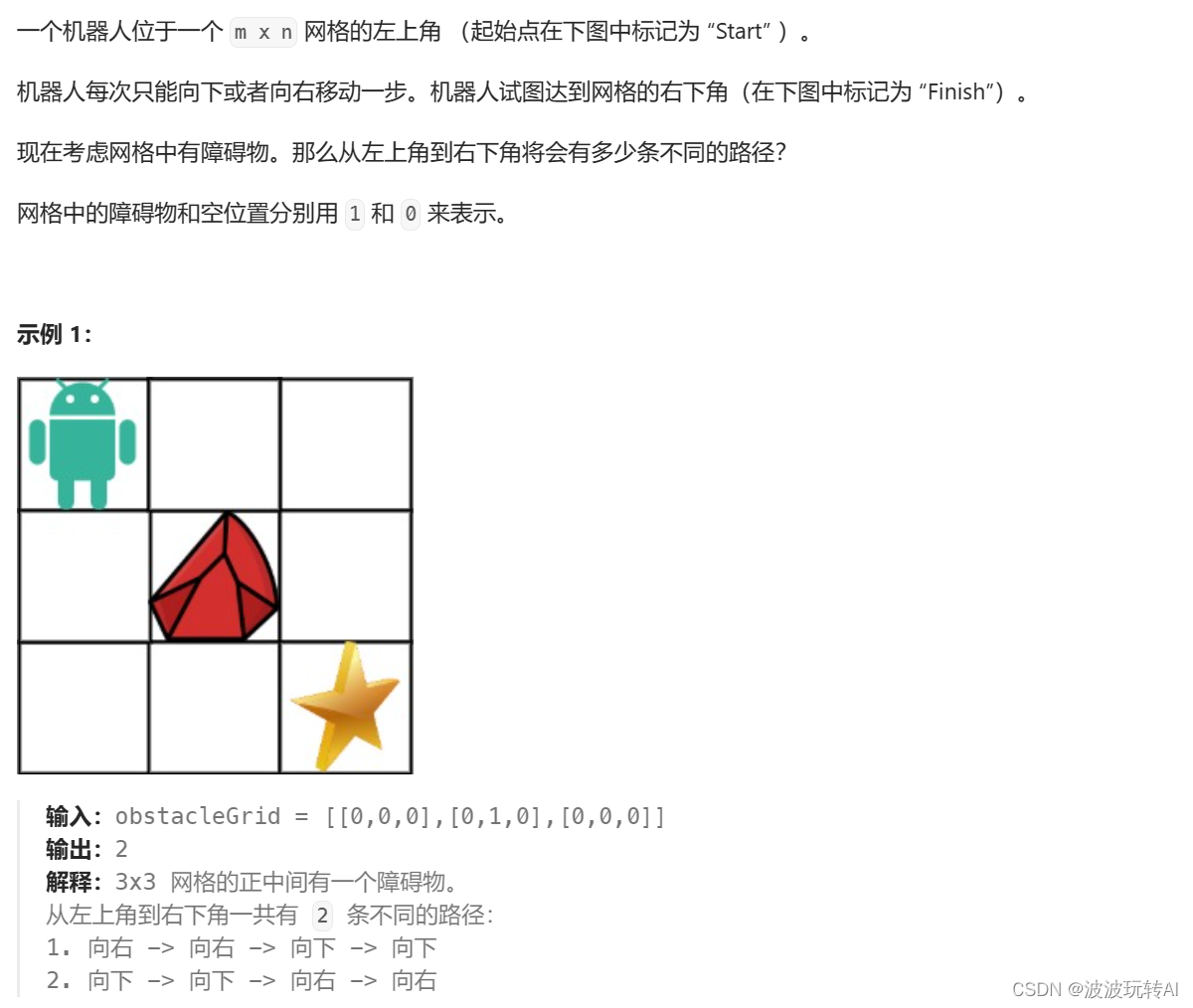
思路:
【注】边界初始化时要注意障碍物,还要考虑到起始点和终止点的障碍物
当网格中没有障碍物时,执行递推公式。
代码:
class Solution:def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:m = len(obstacleGrid)n = len(obstacleGrid[0])if obstacleGrid[0][0] == 1 or obstacleGrid[m - 1][n - 1] == 1:return 0dp = [[0] * n for _ in range(m)]i = 0j = 0while i < m and obstacleGrid[i][0] != 1:dp[i][0] = 1i += 1while j < n and obstacleGrid[0][j] != 1:dp[0][j] = 1j += 1for i in range(1,m):for j in range(1,n):if obstacleGrid[i][j] != 1:dp[i][j] = dp[i - 1][j] + dp[i][j - 1]return dp[m-1][n-1]
7. 整数拆分
题目:

思路:
dp[i]:分拆数字i,可以得到的最大乘积为dp[i]
递推公式:dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});
代码:
class Solution:def integerBreak(self, n: int) -> int:dp = [0] * (n + 1)for i in range(2,n+1):j = 1while j <= i // 2:dp[i] = max(j * (i - j),j*dp[i - j],dp[i])j += 1return dp[n]
8. 不同的二叉搜索树
题目:
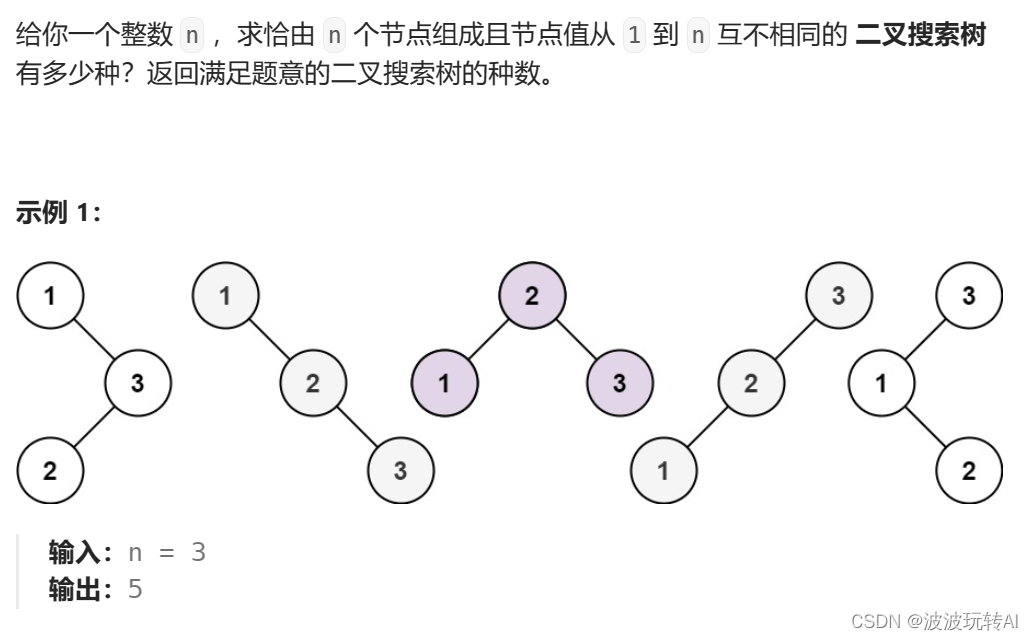
思路:
思路详解
代码:
class Solution:def numTrees(self, n: int) -> int:dp = [0] * (n + 1) # 创建一个长度为n+1的数组,初始化为0dp[0] = 1 # 当n为0时,只有一种情况,即空树,所以dp[0] = 1for i in range(1, n + 1): # 遍历从1到n的每个数字for j in range(1, i + 1): # 对于每个数字i,计算以i为根节点的二叉搜索树的数量dp[i] += dp[j - 1] * dp[i - j] # 利用动态规划的思想,累加左子树和右子树的组合数量return dp[n] # 返回以1到n为节点的二叉搜索树的总数量
相关文章:

动态规划相关题目
文章目录 1.动态规划理论基础2.斐波那契数3.爬楼梯4.使用最小花费爬楼梯5.不同路径6.不同路径 II7. 整数拆分8. 不同的二叉搜索树 1.动态规划理论基础 1.1 什么是动态规划? 动态规划,英文:Dynamic Programming,简称DP,如果某一…...

iOS - Runtime - Class-方法缓存(cache_t)
文章目录 iOS - Runtime - Class-方法缓存(cache_t)1. 散列表的存取值 iOS - Runtime - Class-方法缓存(cache_t) Class内部结构中有个方法缓存(cache_t),用散列表(哈希表)来缓存曾经调用过的方法,可以提高…...

2014年认证杯SPSSPRO杯数学建模B题(第一阶段)位图的处理算法全过程文档及程序
2014年认证杯SPSSPRO杯数学建模 B题 位图的处理算法 原题再现: 图形(或图像)在计算机里主要有两种存储和表示方法。矢量图是使用点、直线或多边形等基于数学方程的几何对象来描述图形,位图则使用像素来描述图像。一般来说&#…...

【物联网项目】基于ESP8266的家庭灯光与火情智能监测系统——文末完整工程资料源码
目录 系统介绍 硬件配置 硬件连接图 系统分析与总体设计 系统硬件设计 ESP8266 WIFI开发板 人体红外传感器模块 光敏电阻传感器模块 火焰传感器模块 可燃气体传感器模块 温湿度传感器模块 OLED显示屏模块 系统软件设计 温湿度检测模块 报警模块 OLED显示模块 …...

Unity中控制帧率的思考
如何控制帧率: 在Unity中,你可以通过设置Application.targetFrameRate来限制帧率。 例如,如果你想将帧率限制为16帧, 你可以在你的代码中添加以下行: Application.targetFrameRate 16; 通常,这行代码会放在…...

阿里云子域名配置,且不带端口访问
进入阿里云控制台,创建一个SSL证书 # 域名名称child.domain.com创建完成后,将返回主机记录以及记录值,保存好,用于下一步使用 创建DNS解析 创建DNS的TXT类型解析 选择记录类型:TXT 填写主机记录:_dnsa…...

C#-ConcurrentDictionary用于多线程并发字典
ConcurrentDictionary 是 .NET Framework 中用于多线程并发操作的一种线程安全的字典集合类。它提供了一种在多个线程同时访问和修改字典时保持数据一致性的机制。 以下是 ConcurrentDictionary 类的一些重要特性和用法: 线程安全性:ConcurrentDictiona…...

深入探讨多线程编程:从0-1为您解释多线程(下)
文章目录 6. 死锁6.1 死锁原因 6.2 避免死锁的方法加锁顺序一致性。超时机制。死锁检测和解除机制。 6. 死锁 6.1 死锁 原因 系统资源的竞争:(产生环路)当系统中供多个进程共享的资源数量不足以满足进程的需要时,会引起进程对2…...
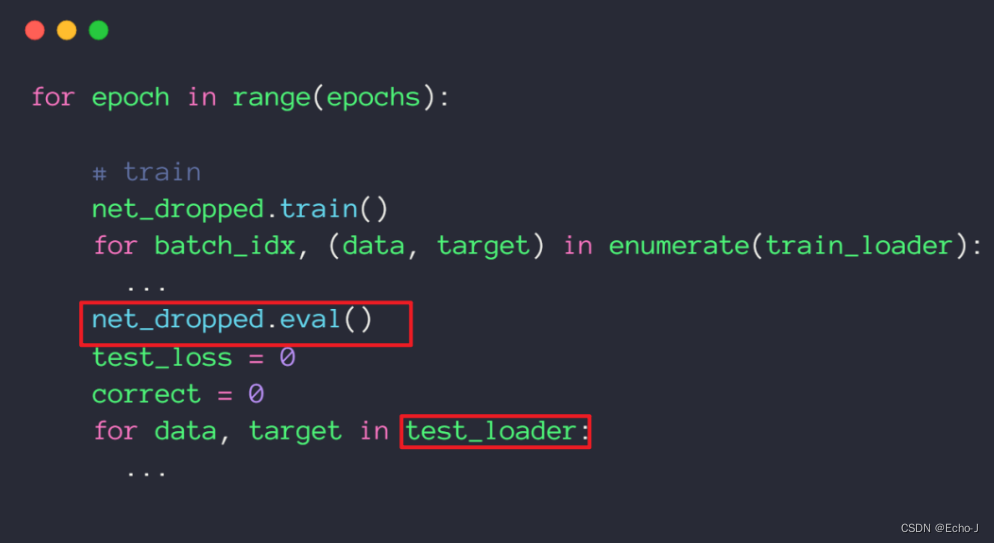
深度学习pytorch——减少过拟合的几种方法(持续更新)
1、增加数据集 2、正则化(Regularization) 正则化:得到一个更加简单的模型的方法。 以一个多项式为例: 随着最高次的增加,会得到一个更加复杂模型,模型越复杂就会更好的拟合输入数据的模型(图-1)&#…...

排序第五篇 归并排序
一 简介 归并排序(Merge Sort) 的基本思想是: 首先将待排序文件看成 n n n 个长度为1的有序子文件, 把这些子文件两两归并, 得到 n 2 \frac{n}{2} 2n 个长度为 2 的有序子文件; 然后再把这 n 2 \frac{n}{2} 2n 个有序的子…...
【Win】使用PowerShell和Webhooks轻松发送消息至Microsoft Teams
Microsoft Teams是一款由微软开发的团队协作和通讯工具。如果您对这个名字还不太熟悉,那么现在就是一个了解它的好时机。微软将Teams定位为其之前Skype for Business解决方案的继任者,并且它也提供了与其他基于频道的通讯应用程序(例如Slack、…...

ESCTF-OSINT赛题WP
这你做不出来?check ESCTF{湖北大学_嘉会园食堂} 这个识图可以发现是 淡水渔人码头 但是 osint 你要发现所有信息 聊天记录说国外 同时 提示给了美国 你综合搜索 美国 渔人码头 在美国旧金山的渔人码头(英语:Fisherman’s Wharf)是一个著名旅…...

2024蓝桥杯省赛保奖突击班-Day2-前缀和、差分、尺取_笔记_练习题解
3月25日-课堂笔记 前缀和预处理 O ( n ) \mathcal{O}(n) O(n) s[1] a[1]; for(int i 2; i < n; i)s[i] s[i - 1] a[i];利用前缀和查询区间和 O ( 1 ) O(1) O(1) long long calc(int l, int r) {return l 1 ? s[r] : s[r] - s[l - 1]; }差分序列的求法 c[1] a[…...

C++基础之虚函数(十七)
一.什么是多态 多态是在有继承关系的类中,调用同一个指令(函数),不同对象会有不同行为。 二.什么是虚函数 概念:首先虚函数是存在于类的成员函数中,通过virtual关键字修饰的成员函数叫虚函数。 性质&am…...

快速入门Kotlin①基本语法
前言 23年底读了一遍“Kotlin官方文档”,官方文档大而全,阅读下来,大有裨益。 此系列文章的目的是记录学习进程,同时,若能让读者迅速掌握重点内容并快速上手,那就再好不过了。 函数 带有两个 Int 参数、…...

【理解指针(四)】
文章目录 一、指针数组二、指针数组来模拟二维数组三、字符指针变量注意: 字符串的例子(曾经的一道笔试题) 四、数组指针变量1、什么是数组指针变量2、数组指针怎么初始化 五、二维数组传参的本质六、函数指针1、什么是函数指针变量2、函数的…...
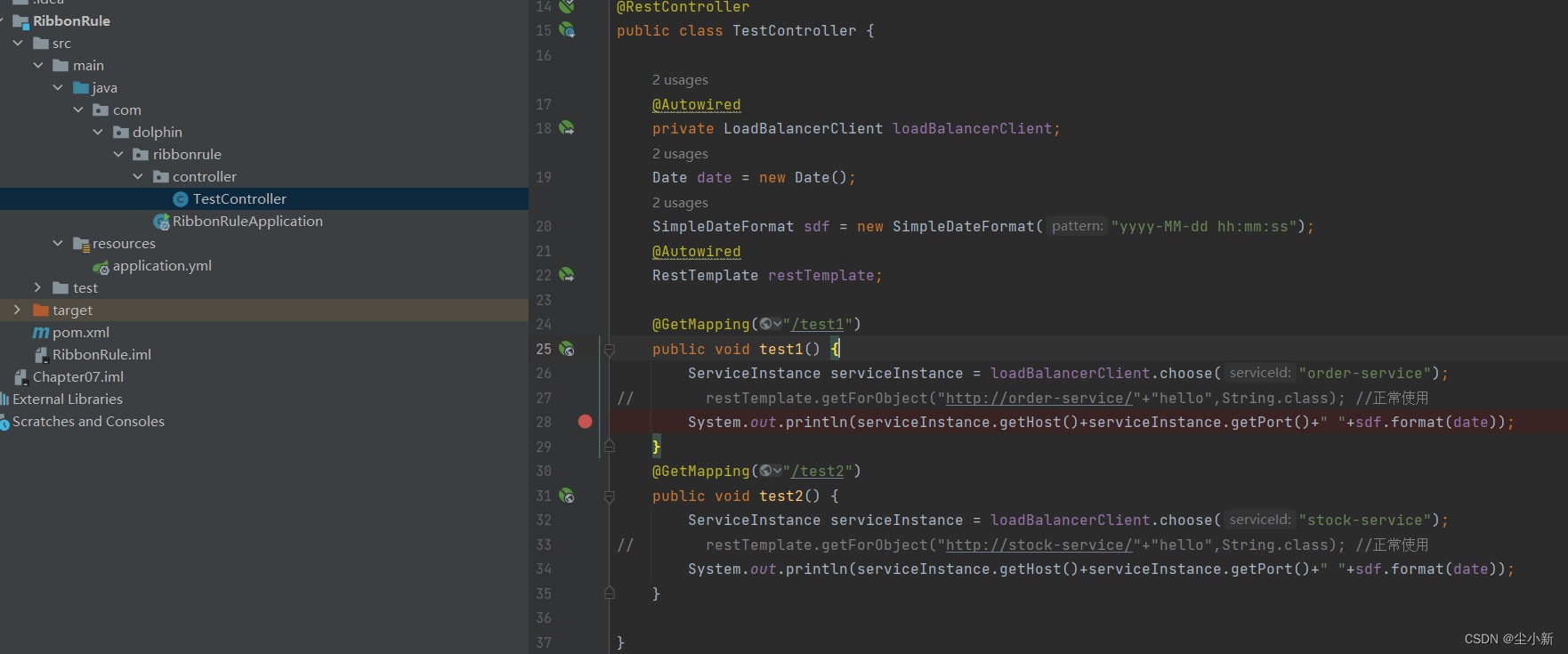
Ribbon简介
目录 一 、概念介绍 1、Ribbon是什么 2、认识负载均衡 2.1 服务器端的负载均衡 2.2 客户端的负载均衡 3、Ribbon工作原理 4、Ribbon的主要组件 IClientConfig ServerList ServerListFilter IRule Iping ILoadBalancer ServerListUpdater 5、Ribbon支持…...

【感悟《剑指offer》典型编程题的极练之路】02字符串篇!
个人主页:秋风起,再归来~ 文章所属专栏:《剑指offer》典型编程题的极练之路 个人格言:悟已往之不谏,知来者犹可追 克心守己,…...

通过 Docker 实现国产数据库 OpenGauss 开发环境搭建
通过 Docker 实现国产数据库 OpenGauss 开发环境搭建 一 前置准备 2.1 下载镜像 docker pull enmotech/opengauss:5.0.1构建镜像的 Dockerfile,方便后期实现个性化定制: FROM ubuntu:22.04 as builderARG TARGETARCHWORKDIR /warehouseRUN set -eux;…...
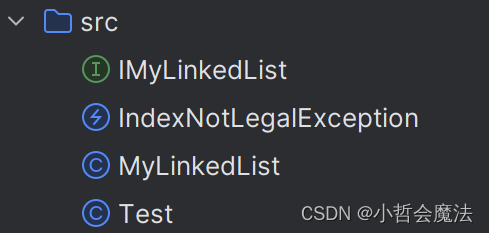
【Java】LinkedList模拟实现
目录 整体框架IMyLinkedList接口IndexNotLegalException异常类MyLinkedList类成员变量(节点信息)addFirst(头插)addLast(尾插)在指定位置插入数据判断是否存在移除第一个相等的节点移除所有相等的节点链表的长度打印链表释放回收链表 整体框架 IMyLinkedList接口 这个接口用来…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
